基于GP-XGBoost的大坝变形预测模型

徐 韧，苏怀智，杨立夫

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;2.河海大学水利水电学院，江苏 南京 210098)

大坝作为重要的基础设施，其安全关乎民生，加强大坝性态监测是保障大坝安全的重要举措，而坝体的变形情况能够直观反映其性态，是判断大坝服役期间状态的重要依据[1-2]。随着自动监测设备投入使用，坝体变形监测数据延续性更好、时效性更强、稳定性更佳，样本基数较人工观测时更大。而传统算法如灰色模型理论在大数据预测中效果欠佳[3]，BP神经网络在长周期数据预测中易过拟合[4]，基于时间序列的模型其参数在大时间跨度预测时敏感性较差[5]。

近年来，随机森林、AdaBoost、Bootstrap等集成学习算法因其速度快、精度高、鲁棒性好的特点被学者运用在大坝变形预测领域。罗浩等[6]通过随机森林算法，基于水压分量、温度分量、时效分量对拱坝位移进行了预测。沈晶鑫等[7]将AdaBoost算法与优化神经网络相结合，利用AdaBoost算法将粒子群优化后的神经网络模型集成，建立了大坝变形预测模型，并对向家坝第七坝段变形进行预测。王晓玲等[8]基于Bootstrap和改进布谷鸟算法建立了混合模型，利用混沌理论和惯性权重理论以改善模型易陷入局部最优的问题，成功实现了大坝性态评价。极端梯度提升 (extreme gradient boosting，XGBoost)算法由华盛顿大学陈天奇博士提出，是一种可进行并行计算的集成算法，通过加入正则项来控制模型复杂度，有效降低过拟合概率，能较好地解决传统模型存在的过学习、预测效率低、训练时间长、只适用于小集群样本等问题[9]，已在交通流量预测、商品销售量预测、疾病诊断等领域取得成功应用[10-12]，目前在大坝安全领域应用较少。

为提高大坝安全预测模型的预测精度及训练速度，提升大坝安全监测系统对于数据噪音的响应能力，本文采用XGBoost算法对大坝变形数据进行预测，并引入贝叶斯优化，通过高斯过程(GP)对模型参数进行优化，建立基于GP-XGBoost的大坝变形预测模型，并结合原型观测数据对模型拟合预测能力进行评价。

1 建模原理

1.1 大坝变形预测统计模型基本原理

水压、温度等环境量的变化会导致坝体产生可逆变形，而时效因子则引起坝体材料劣化、力学性能下降从而形成不可逆影响[13]。构建大坝变形预测模型时常选择水压因子、温度因子、时效因子作为影响因子[14-15]。坝体位移公式为

δ=δH+δT+δθ

(1)

式中：δ为坝体位移；δH、δT、δθ分别为位移的水压分量、温度分量和时效分量。

1.2 基于XGBoost算法的大坝变形预测模型构建原理

XGBoost算法是梯度提升机器(gradient boosting machine，GBM)算法的扩展，是一种同时具备线性模型和树模型特点的优化模型，能够同时完成回归和分类任务。XGBoost算法由多棵决策树(CART)组成，通过决策树集成实现机器学习，所有决策树的预测值相累加即为模型预测值，并由梯度提升决策树(gradien boost decision Tree，GBDT)算法进行模型训练[16]。与GBDT算法不同的是，XGBoost算法通过对损失函数进行二阶泰勒展开以快速逼近目标函数，并加入了正则项调节参数以避免过拟合，训练速度快，预测精度高[17]。

在构建大坝变形预测模型时，XGBoost算法通过在变形预测函数中不断加入关于各因子的新函数来逼近实测变形值，即：

(2)

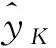
XGBoost算法目标函数定义如下：

(3)

式中：L为损失函数，用于评估变形预测值与真实值之间的损失；Ω(fK)为正则化函数，用于控制控制模型复杂度，避免过拟合。正则化函数定义如下：

(4)

式中：γ、λ为正则项惩罚系数；ω为叶子节点对应的权重；T为温度。对(2)式改写并作二阶泰勒展开：

(5)

可以对公式(5)进行进一步简化得：

式中：gi为损失函数的一阶梯度统计;hi为损失函数的二阶梯度统计。通过迭代找到f(x)使目标函数最小则模型训练完成。

1.3 基于高斯过程(GP)的预测模型参数优化原理

贝叶斯优化算法(Bayesian optimization)是一种高效的优化工具[18]，其基于不同代理模型可分为3类：树型评估器TPE、随机森林回归AMAC和高斯过程GP。大坝原型观测数据集庞大，特选用迭代速度较快、质量较高的高斯过程作为优化模型内核。

以高斯过程为内核执行优化任务时，常对目标函数f(x)假设一个满足高斯过程的先验分布模型，即模型各参数任何有限维度的组合仍满足高斯分布：

f(x)～GP(E(f(x)),COV(x,x′))

(8)

式中：E为f(x)的数学期望；COV(x,x′)为x的协方差。每个参数组合{x1,x2,…,xi}都属于高斯分布，满足以下公式：

(9)

在先验分布函数确定后，采样对模型进行修正。样本越多，模型越精确。为提升采样速度，优化算法通过定义采集函数确定下一个采样点[19]。采集函数将权衡模型优化方向为探索(exploration)或开发(exploitation)，探索将在新的区域采样以避免局部最优，开发则在现有局部最优解附近开展进一步搜索，尝试寻求全局最优解[20]。优化目标则是在全集Α中寻找使f(x)值达到最大或最小的X集合如下式所示：

x*=argmaxx∈Αf(x)

(10)

1.4 K-折交叉验证

交叉验证值CV常作为模型优劣评价指标。K-折交叉验证(K-fold cross-validation)是交叉验证的一种。调用交叉验证函数时，先将数据集均分为K份，选择其中一份作为验证集，其余K-1份则用于训练模型，如此执行K次，将得到的K个评价值求和平均即为交叉验证值CV[21-22]。评价值的类型根据大坝观测数据特点选用均方根误差RMSE(Root Mean Square Error)。

2 建模步骤

建模流程如图1所示，具体步骤如下。

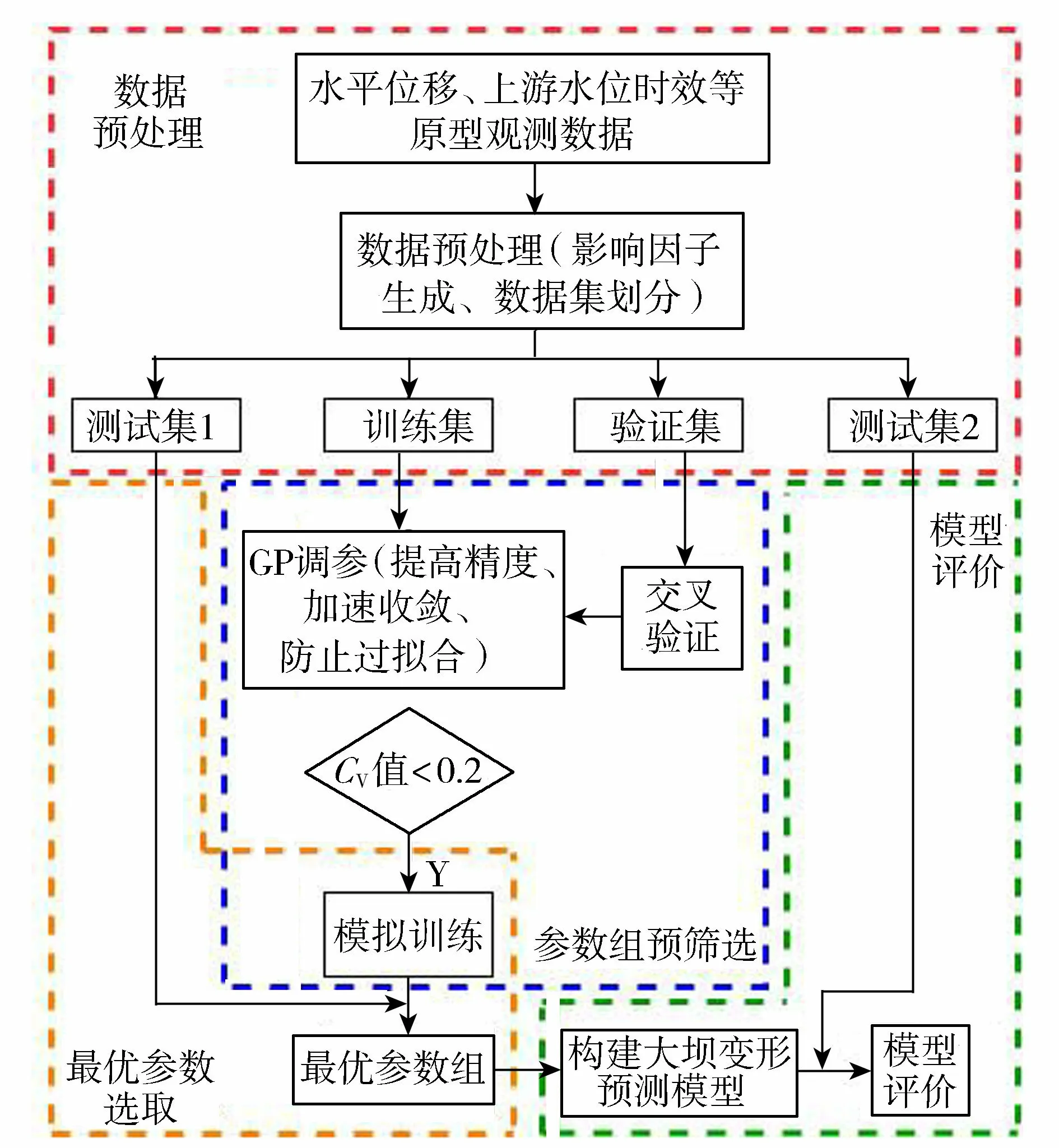
图1 基于GP-XGBoost算法的建模流程

步骤1对上游水位、坝体上下游方向水平位移及时效数据进行处理，整理为合适影响因子作为输入样本集，并将其划分为训练集、验证集、测试集1、测试集2，其中验证集由交叉验证函数从训练集中划分。

步骤2划分好的训练集与验证集通过交叉验证产生评价指标CV，确定各参数优化范围，带入贝叶斯优化算法进行优化迭代。由于验证集取自训练集内部，为避免局部最优和预测值突变的情况，选取CV值小于最大CV值10%(本次选取0.2)的参数组构建预测模型[23]，对训练集1进行预测，若所选参数组均出现局部最优或预测值突变则适当放宽CV阈值，综合选取最优参数组。综合评价各参数组训练速度与预测精度，选取最优参数组构建基于GP-XGBoost的大坝变形预测模型。

步骤3将测试集2中的数据带入步骤2中构建的模型，用于模型评价，通过与基于默认参数的XGBoost算法、线性回归方法、BP神经网络所建立的模型进行比较，对GP-XGBoost模型做出评价。

3 工程实例验证

某水库为混凝土双支墩肋墩坝，控制流域面积570 km2，总库容3.47亿m3，是一座具有防洪、灌溉、发电、养殖等综合功能的年调节的大(2)型水库。选取2015年1月至2018年3月共1 174组上游水位数据及PL5测点在上下游方向的水平位移测值作为初始数据集进行分析。其中PL5测点位于5号坝段坝顶，为自动测点，采用垂线法采集水平位移数据。

3.1 数据预处理

PL5测点上下游方向水平位移、上游水位均为一天一测，数据较完整，自2015年1月至2017年12月，水平位移与上游水位一一对应，其中水平位移与水位过程线如图2所示。

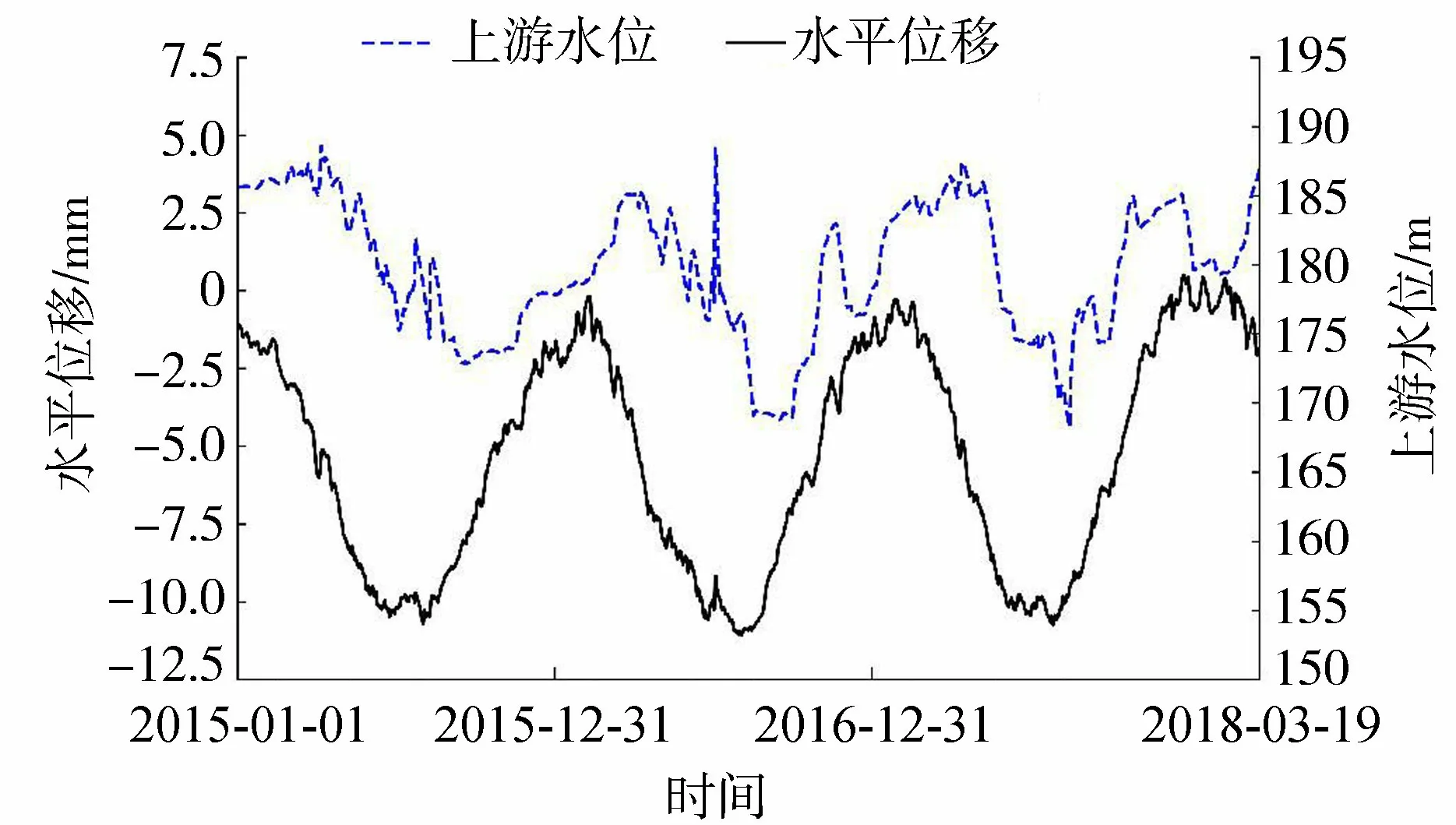
图2 磨子潭水库PL5 测点位移与上游水位过程线

将输入样本集前600项划分为为训练集，601～800项划分为测试集1，其余划分为测试集2。验证集由内置交叉验证函数在训练集中自动生成，并在训练过程中生成模型评价指标CV。

3.2 参数优化

对各关键参数进行初值定义，选定优化范围，具体参数含义、初值及取值范围如表1所示。

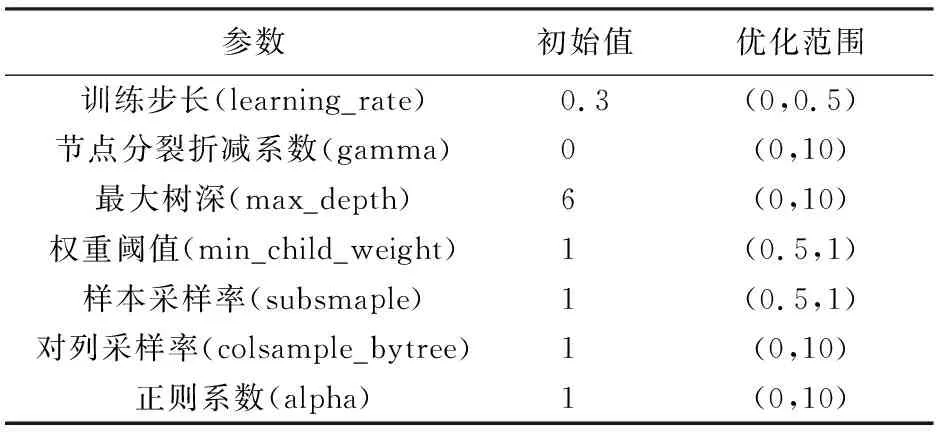
表1 参数优化初值、范围及含义

将表1中的参数组带入贝叶斯算法中迭代2 000次，取出2 000种参数组合中CV值小于0.2的5组，如表2所示。

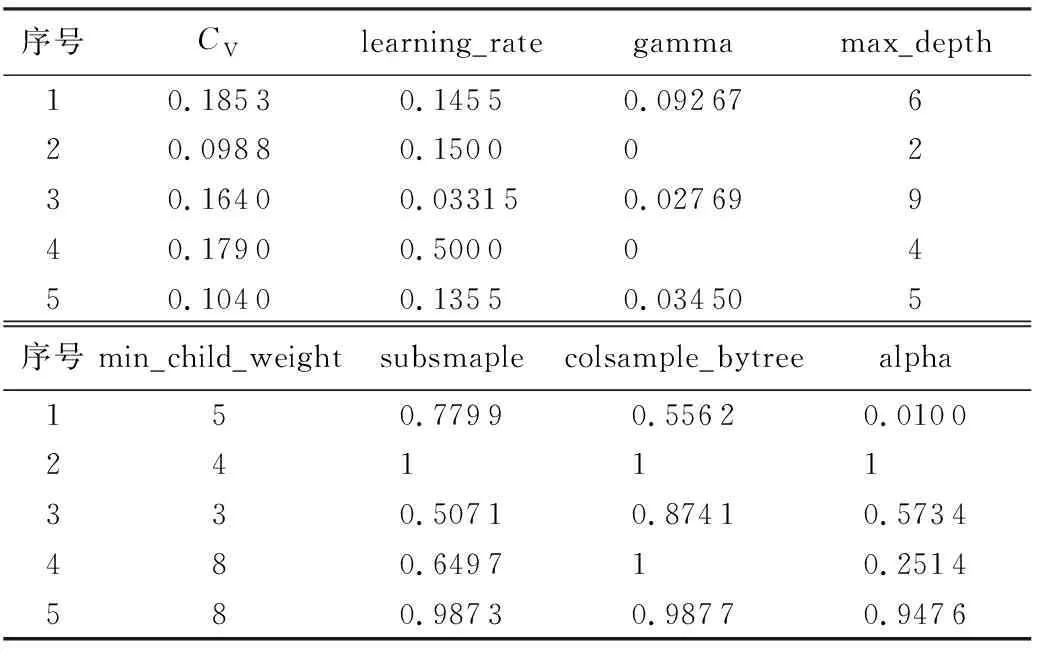
表2 最优参数组

将5组参数分别带入XGBoost建模并对测试集1进行预测，迭代次数设置为600。各参数组对测试集1预测情况如图3所示，其中第2参数组预测RMSE值最小为0.904 91。其中11月至12月变形预测数据出现小范围突变，其原因归结为此时段内坝体水压分量突然增大，模型参数max_depth对于突变数据较为敏感，当参数max_depth取值偏大时，预测值突变较明显，通过贝叶斯优化调整参数取值，选取合适的max_depth值可以缓解预测值突变的情况，如第2参数组所示。若根据条件CV<0.2所选参数组建模预测均出现明显突变，则应适当扩大参数组选取范围，权衡各参数在合适范围做出选择。

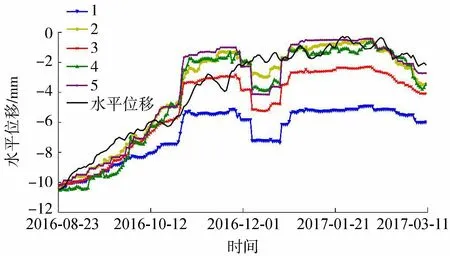
图3 不同参数组预测结果

5组参数组训练迭代收敛情况如图4所示。由图4可知，第4组参数建模收敛速度最快，但第2组参数建模在预测精度较高的条件下也满足了运算速度需求，综上所述，将选择第2参数组构建变形预测模型，用于精度评价。

图4说明预测模型最多经过200次迭代即可收敛，在后续的运算中将迭代次数缩减为300次以提升学习效率。

图4 模型训练迭代过程

3.3 模型对比评价

针对回归模型选用均方根误差(RMSE)、平均绝对误差(MAE)、拟合优度(R2)作为精度评价指标，分别用于评价模型稳定性、精确度及拟合效果。

将基于GP-XGBoost算法的预测模型与未经过参数优化的XGBoost预测模型、线性回归模型、BP神经网络模型训练并对测试集2进行预测，对各模型的精度进行比较，评价模型性能。具体模型训练结果、预测结果及残差计算结果如图5所示，预测精度评价结果如表3所示。

表3 各模型预测精度评价

由图5可知，基于GP-XGBoost建立的预测模型在水位突变的时段能够很好地对坝体水平位移进行预测，且整体精度高，拟合效果好，收敛速度快。BP神经网络模型在预测阶段有时会出现过拟合的现象，而XGBoost模型加入了正则项参数，通过选择合适的参数值有效避免过拟合。由表3可以看出线性回归模型的拟合优度也较高，但线性回归模型优势在于反映线性趋势，呈现局部复杂变化较为困难，如6月底及12月初的线性回归模型预测数据难以体现坝体变形短期的波动，而基于GP-XGBoost所建立的大坝变形预测模型，预测值可以较好吻合坝体实际变形波动过程(图5)，有助于大坝性态分析。实例中基于GP-XGBoost所建立的模型预测误差相较于传统模型明显较小，拟合更平滑、精度更高、模型更稳定，对于大变形预测将更具优势。参数优化能够进一步提升XGBoost算法模型的精确度，优化拟合效果，使模型能够很好地满足大坝变形预测的工作需求。

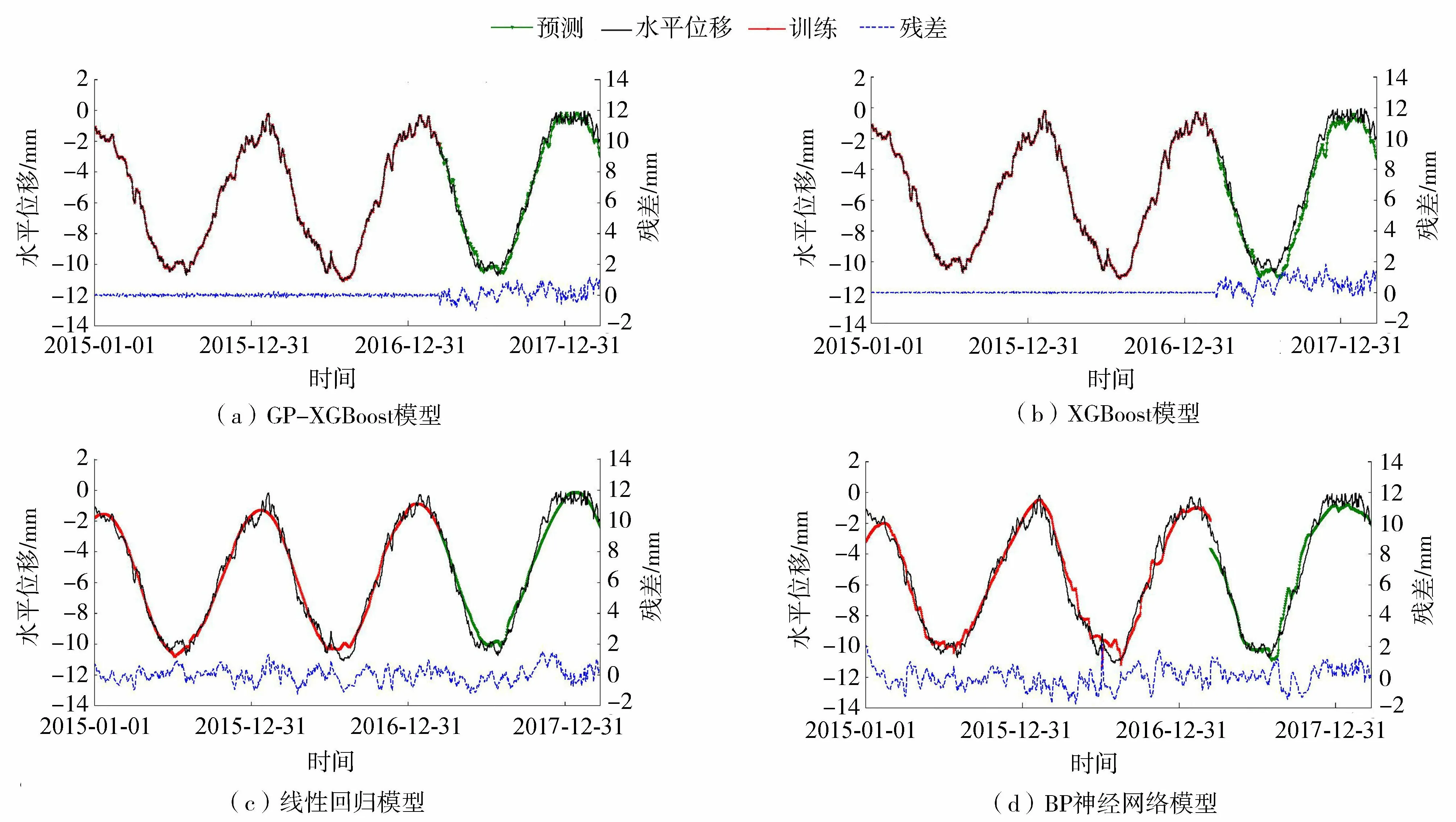
图5 各模型预测结果对比

3.4 特征重要性分析

选择特征分裂率、特征平均收益率、特征平均覆盖率3个特征来衡量各分量在基于GP-XGBoost构建的大坝变形预测模型中占水平位移的比重。其中特征分裂率表示因子对大坝变形的参与度，通过统计某个特征的分裂次数确定。特征平均收益率表示因子对大坝变形的影响率，通过损失函数的变化ΔL度量。特征平均覆盖率表示因子对大坝变形的贡献度，通过节点的二阶梯度hi表征，特征平均收益率与特征平均覆盖率的计算方法如式(11)(12)所示。其中各因子互相独立，分别进行计算。

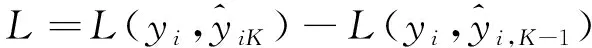
(11)

(12)

结果通过交叉验证互相比对，本次计算各因子交叉验证结果一致，具体结果如表4所示。由表4可知，温度分量占大坝变形最大比重，其特征平均收益率达98%，选择温度因子作为分裂结点可以使预测函数快速接近真实值，且温度分量对大坝变形的速率影响最大。同时温度因子特征分裂率、特征平均覆盖率都接近50%，表明温度分量与大坝变形联系较强，对变形的贡献较大。水压与时效分量对大坝变形速率影响较小，但对变形的大小有一定的影响。

表4 各因子特征重要性 单位：%

结果表明，对坝体温度进行实时监测、控制可以有效帮助大坝健康服役，控制大坝变形速率，减少变形量，增加大坝维护工作的容错率，增强大坝变形的可控性。应对冷却管道等温控设施进行定期检查，对于坝体温度较高部分重点防护，降低坝体开裂风险。

4 结 语

a.XGBoost算法通过加入正则项参数，限制拟合程度，有效避免过拟合。且多决策树叠加保证了计算精度，对目标函数进行二阶泰勒展开大幅提升迭代速度，能够很好地适应大坝原型监测数据周期长、数据量大、精度要求高的特点。

b.基于高斯过程的贝叶斯优化函数能够探索开发最优参数组，进一步提高模型的精度、稳定性，拟合更加平滑。基于磨子潭水库原型观测数据建立的大坝变形监测模型的成功应用证明， GP-XGBoost为大坝安全监测提供了一种良好的思路。

c.XGBoost是一种集成算法结合的树型算法，其包含了树型算法在预测过程中难以突破训练样本峰值的缺点。大坝上游水位在汛期上涨迅速，极有可能超过训练样本峰值，峰值限制问题将是今后的研究方向。