基于博弈论的区域铁路通道线间竞争及协同发展研究

吴琪

（中国铁路设计集团有限公司 工程师，天津 300308）

0 引言

随着人民生活水平提高，铁路旅客出行需求的急剧上升，目前我国铁路建设仍处于处于快速发展的时期，区域铁路通道趋于完善：上海至南京、广州至深圳、北京至天津等通道已经实现三线并行，成都至重庆等通道正在建设推进中，高速铁路与城际铁路分担了既有线上的一部分客流，既有线的运输能力和运输压力进而得到释放。铁路通道客运产品在一定程度上反映了区域铁路的运输效益与服务水平，因此精准把握不同设计标准的线路功能定位，即优化客运产品的设计不但能够缓解出行需求增长带来的压力，而且可以最大化铁路客运企业的效益。张拥军[1-3]等人采用多目标、多层级的整数规划模型，来解决铁路客运产品中高速列车的停站方案，通过组合数值的方法进行了模型求解。滕志民等人[4-9]基于实现铁路运输企业获取最大效益的角度，深入探讨各个利益相关方的关系，最后通过通道内外的划分方式对运输产品效益分别进行了研究。

综上所述，虽然国内外学者对铁路通道客运产品中例如列车开行种类、对数、频率、区段、停站方案等研究较为丰富，但是对于同一区域铁路通道并行的铁路线，没有较好地研究并行线间的客流分配问题。因此本文将区域铁路通道线间客流分配作为研究重点，区分区域铁路通道内因设计运行速度、列车开行频率、列车票价、旅客舒适度等方面的差异性所导致的功能定位，运用线间博弈模型，进一步探究铁路运输企业的最大化收益策略。

1 基于博弈论的区域铁路通道线间客流分配模型

本文假定（1）区域铁路通道既有线：区域铁路通道既有线仅运行货运列车，且不作为重点研究；（2）区域铁路通道城际线：区域铁路通道城际线仅运行旅客列车，不运行货物列车；（3）区域铁路通道高速线：高速旅客列车作为区域铁路通道高速线上唯一运行的列车类。既有线、城际线以及高速线均分布在相同区域内，线位假定基本平行。

1.1 区域铁路通道旅客出行效用理论

1.1.1 旅客出行效用函数

旅客在产生出行需求时，不同旅客会对同一种运输方式持有不同的考虑或态度，每个人也会根据各自偏好对票价和自身购买承受能力进行权衡比较，因此将对不同的运输方式的认同度或满意度有所不同，即为旅客出行效用[10-11]。在实际出行中，旅客通常选择的出行方案是效用值最大的方案，对选择行为进行量化，公式如式（1）[12]。

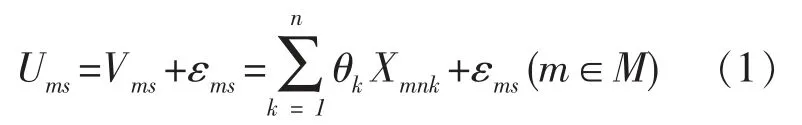
式中：Ums为旅客S使用运输方式m的出行总效用；Vms为旅客S使用运输方式m的效用固定项；εms为旅客S使用运输方式m的效用概率项；θk为影响因素特征的参数；Xmnk为旅客S使用运输方式m的影响因素向量；M为高速线和城际线两种运输方式的集合。

高速线与城际线的选择概率模型公式如式（2）。

1.1.2 影响因素向量选择

1.1.2.1 经济性Em

在同一区域铁路通道内，不同标准或等级的客运产品从经济性方面主要表现为客票价格的差异性，本文设定其经济性即为运行里程与运价率的乘积。其计算公式如式（3）。

式中：Em为选择运输方式m需要支付的效用；Rm为运输方式m的运价率，通常即为每公里的效用；Lm为选择运输方式m的出行总距离。

1.1.2.2 速度性Fm

不同线路标准的设计行车速度不同，因此列车实际开行中的旅行速度和旅行时间均存在不同差异[13]。本文设定其速度性即为旅客出行中选乘运输方式m所产生的时间价值效用，计算公式如式（4）。

式中：Fm为选择运输方式m产生的时间价值效用；Lm为选择运输方式m的运行里程；Tm为选择运输方式m产生的旅行时间；vm为运输方式m的运行速度；VOT为通道内的旅客出行时间价值。

结合文献资料[11]并参照生产法，铁路通道内旅客出行的时间价值计算公式如式（5）。

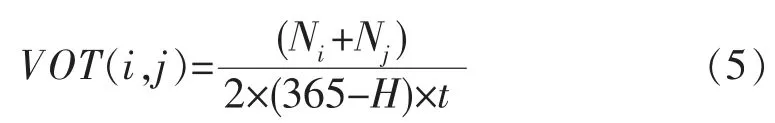
式中：VOT（i，j）为车站i至车站j的时间价值；Ni、Nj为地方i、地方j的人均国民产生总值；H为法定节假日天数；t为每人一天平均工作时间。

1.1.2.3 舒适度Cm

旅客舒适度即为旅客在出行途中所体验的舒适程度，对于技术标准不同的线路来讲，舒适度的差异主要表现在旅客乘车途中感受疲劳程度的不同[14]。一般情况下，乘坐同一交通工具的旅行时间越长，旅客感受到的疲劳值越大，舒适度相应越低，反之亦然。因此，计算旅客舒适度公式如式（6）和（7）。

式中：Cm为选择运输方式m的舒适度；TCm为旅客疲劳恢复时间；αm、βm、c为舒适度的参数；I为最长恢复时间；Tm为选择运输方式m产生的旅行时间。

1.1.2.4 服务频率fm

通道内线路的服务频率即为开行旅客列车的平均发车间隔的倒数，公式如式（8）。

式中：fm为运输方式m的服务频率；△Tm为运输方式m的平均发车间隔。

综合上述各因素，对旅客出行的效用函数进行优化细化，公式如式（9）。

式中：Ums为旅客S选择运输方式m的出行总费用；θ0s为旅客S对运输方式m的偏好参数；θns(n=0,1,2,3,4)为运输方式m的特征参数，可通过软件SPSS中的多项Logistic估算特征参数；Ems为运输方式m的经济性指标；Fms为运输方式m的速度性指标；Cms为运输方式m的舒适性指标；εms为旅客使用运输方式m的效用概率项。

此时，通道内高速线与城际线的客运分担率为公式（10）。

式中：MPms为旅客S选择运输方式m出行的概率；Ums为旅客S选择运输方式m出行所产生的费用。

1.2 基于博弈论的区域铁路通道线间客流分配模型

1.2.1 博弈模型的假设

为简化计算流程，在对研究结果不产生干扰和影响的前提下，突出主要问题与模型关键影响因素间的关系，故作假设如下：

1）区域铁路通道已经实现三线并行，且既有线仅运行货运列车。

2）博弈中，单一旅客的出行偏好始终保持不变，对旅客年龄、性别及职业等因素不做过多考虑。

3）仅将经济性、舒适性、速度性、运输服务频率作为影响运量的主要因素。

4）各线不存在票价浮动或临时打折活动，且定价不考虑受国家政策调控影响。

5）通道内高速线与城际线的运输能力能够充分满足旅客运量需求。

6）通道内高速线与城际线运行列车座位的数量、席别、比例相同，商务座暂不考虑。

1.2.2 合作博弈模型的建立

高速线和城际线间的博弈，实际目标是为了实现铁路运输企业收益的最大化。结合上述内容，通过对客票价格实施调整，研究其与客量的多种策略组合，实现双方的最大效益[9-10]。运用区域通道的整体运输合作收益、运输成本以及运量等函数，搭建通道内线间客流分配模型，为后期铁路客运产品设计及其他区域通道内的铁路建设提供参考借鉴。

1.2.2.1 区域通道客运合作收益函数

区域通道客运合作收益函数包括运输价格、成本以及客运收入等主要部分，公式如式（11）和（12）。

式中：u总为高速线与城际线的收益总和；um为选择单一运输方式m的收益；为n次博弈后，车站i至车站j间的总运量；Tijm为选择运输方式m由车站i至车站j的旅行时间；fijm为运输方式m在车站i至车站j的服务频率；Pijms为运输方式m由车站i至车站j所产生的旅行费用；Cm为运输方式m所产生的运输成本。

1.2.2.2 客流量函数

结合上述研究可知，以调整票价的方式获取通道整体最大收益时，高速线和城际线能够吸引并转移一部分计划选乘其他交通工具出行的客流，主要来自公转铁或搭乘民航的客流，因此铁路客运的需求攀升，整个通道的铁路运量发生增长。诱增客流的发生在受交通工具自身条件优劣影响的同时，也会受旅客的对于出行成本、支付能力、偏好心理等因素的影响。综上，通过引力模型计算运量吸引率，公式如式（13）。

式中：Qij为车站i至车站j的运量；MiMj为车站i至车站j的客流吸引因素；β为模型参数，取

对通道内高速线与城际线来讲，在同一时间里是非变量，票价调整后吸引率η符合公式（14）。

由此得出诱发量δ公式（15）。

因此，客流量函数公式如式（16）。

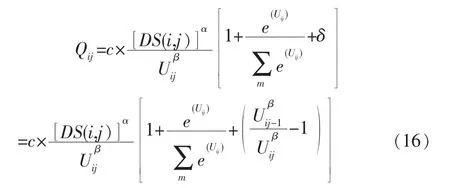
式中：Uij为车站i至车站j的出行费用；DS(i,j）为地方i与地方j的经济社会发展情况（如人口规模、消费水平等）；为运输条件变化前后的出行效用；c、α、β为模型参数，在0-1区间取值。

将高速线与城际线预测运量作为原始数据，运用分担模型得到各自的运量，公式如式（17）。

式中：为n-1次博弈后，区间总运量；为n次博弈后，旅客选择运输方式m的出行费用；β为模型参数。

n次博弈后，各运输方式运量公式如式（18）。

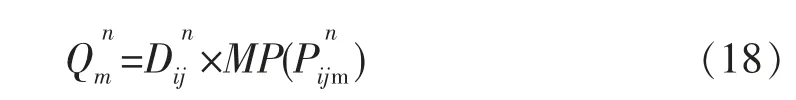
式中：为运输方式m在n次博弈后的运量；为客运分担率。

1.2.2.3 成本函数

鉴于高速线、城际线同属铁路运输，因此设定固定成本与基础成本之和均为两线运输方式的运输成本，固定成本主要由列车运行的设施设备等方面费用组成，基础成本主要是由单位能耗费用组成，公式如式（19）。

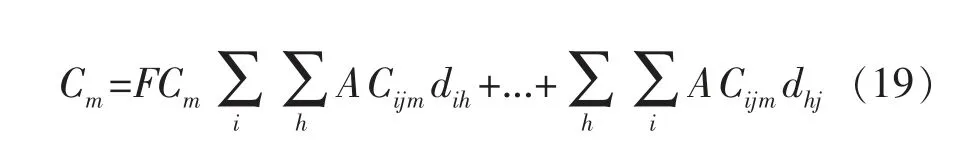
式中：FCm为选择运输方式m的固定成本；ACijm为选择运输方式m的区间单位平均成本；dih为车站i至车站h的距离；dhj为车站h至车站j的距离。

1.2.2.4 合作博弈模型

同竞争博弈模型相似，票价作为主要影响因素，在每一次博弈后，均产生一个收益及双方收益总和，关系公式如式（20）。

最后，通过启发式算法得到总收益usum的最大值，此时满足式（21）。

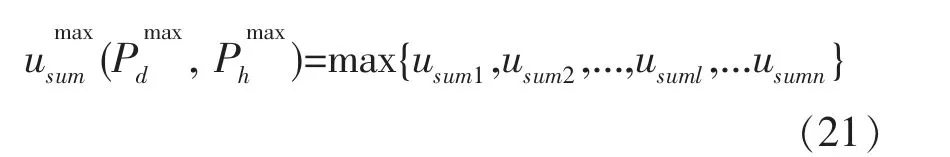
1.2.3 竞争博弈模型的建立

目前，我国铁路运营由国铁集团负责统一管理，随着地方政府对区域铁路运营的积极性和主动性愈加强烈，成立新的运输企业或运营公司，将在区域铁路通道内出现不同标准等级和功能定位的线路间开展竞争博弈的局面。本文建模中假设前提不考虑因票价浮动产生的公转铁、航转铁现象，即在竞争中形成零和博弈。因此，在建立模型中引入高速线与城际线的收入函数、客运量函数和成本函数，形成两线竞争博弈模型。

1.2.3.1 客运竞争收益函数

区域铁路通道内的客运竞争收益函数由运输价格、运输成本及收入构成，公式如式（22）。

式中：um为运输方式m的收益；为n次博弈后，从车站i至车站j的总运量；Tijm为运输方式m的区间旅行时间；fijm为运输方式的区间服务频率；Pijms为运输方式m的旅行费用；Cm为运输方式m所产生的运输成本。

1.2.3.2客流量函数

因总运量在零和博弈中保持不变，即上述预测总运量，得到高速线和城际线运量公式如式（23）。

式中：为n-1次博弈后，车站i至车站j的运量；η为客流吸引率；为n次博弈后，车站i至车站j的旅客出行效用；β为模型参数。

在通过n次博弈之后，高速线与城际线的运量计算公式如式（24）。

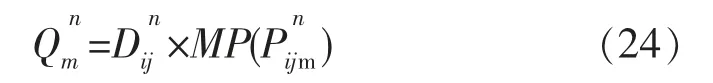
式中：为运输方式m在n次博弈后的运量；为运输方式m在n次博弈后的客运分担率。

1.2.3.3 竞争博弈模型

前文已假定票价为线间客流的唯一影响因素，且运量Qm与出行效用Pm的互为函数关系，竞争收益函数um与出行效用Pm的同为函数关系，因此，在高速线和城际线的竞争中，出行效用Pm的改变将产生新的运量Qm，进而产生新的竞争收益um，关系公式如式（25）。

假设与作为最优方案下的纳什均衡票价，如下。

令上式对Pd和Ph求偏导数为0，如式（28）和（29）。

2 基于启发式算法的线间客流分配模型求解

2.1 合作博弈模型求解

高速线与城际线在通道内通过合作而获得的最大收益就是合作博弈下的最优解，模型求解条件公式如式（30）。

式中：umax为高速线和城际线的最大收入；u为单方最大收入与该策略下的另一方收入和；为运输方式m在t次博弈后的最优票价；为高速线的区间票价取值；为城际线的区间票价取值。

将高速线和城际线的合作博弈分成三步。

步骤一：根据实际情况，对两线客运量、票价、基础参数等进行初始化赋值。

步骤二：结合高速线与城际线的客流量与票价范围取值，依次进行迭代，不断调整双方票价，并按照当前票价下的区域铁路通道两线总体收益判定是否进一步迭代。若票价改变后两线的总收益不低于上一次收益的数据，便对初始值赋予改变后的运量、票价、收益等数据，同时不断进行迭代至最大迭代次数，或不再出现更高的收益数值时即可终止。

步骤三：迭代终止后输出最优解，即两线最大收益值。对比竞争博弈模型下的最优解，分析区域铁路通道高速线与城际线在合作与竞争博弈中，铁路运输企业或客运部门如何决策才能实现效益的最大化目标。

2.2 竞争博弈模型的求解

建立两线的竞争博弈模型，进行纳什均衡计算求解，直到博弈双方的策略均为最优。求解竞争博弈模型条件公式如式（31）。

式中：为最优均衡收入；为t次博弈后的均衡收入；为运输方式m的均衡票价；为t次博弈后，运输方式m的均衡票价；为高速线的区间票价取值；为城际线的区间票价取值。

纳什定理指出，凡是有限次的博弈就至少存在一个纳什均衡，因此该竞争博弈模型必然存在纳什均衡解，将高速线与城际线的竞争博弈分成三步。

步骤一：根据实际情况，对两线客运量、票价、基础参数等进行初始化赋值。

步骤二：结合高速线与城际线的客流量与票价范围取值，依次进行迭代，不断调整双方票价，并按照当前票价下的各线收益判定是否进一步迭代。若票价改变后单一线路的收益不低于上一次收益的数据，便对初始值赋予改变后的运量、票价、收益等数据，同时不断进行迭代至达成纳什均衡时终止。

步骤三：迭代终止后输出纳什均衡解，即输出两线最优的运量、票价、收益、分担率等数值。

3 实例分析

3.1 胶济通道各线路概况分析

胶济铁路通道是贯穿齐鲁的运输“大动脉”，衔接山东省内两座主要城市济南和青岛，是山东半岛与省内乃至全国各地实现客货运输快速交流的干线通道，同时也是济南局集团公司最为重要的“黄金通道”。如今，胶济通道上的胶济铁路、胶济客运专线、济青高铁已实现 “三线并行”，2019年（2020年受疫情影响，数据不具代表性）通道内旅客发送量约为7 404万人、货运量约为1.15亿t，分别占到济南局集团公司总量的46.1%和23.9%。

3.2 基于博弈论的胶济通道线间客流分配

3.2.1 旅客出行效用及参数计算

旅客出行效用参数θns(n=0,1,2,3,4)即代表旅客在对出行行为做出选择时，各相关因素指标对其影响程度大小。本次研究参照胶济通道现有数据资料同时结合其运营情况，采取专家打分法对参数θns开展评估。通过计算梳理本线与跨线旅客，得到参数θns的取值见表1所示。

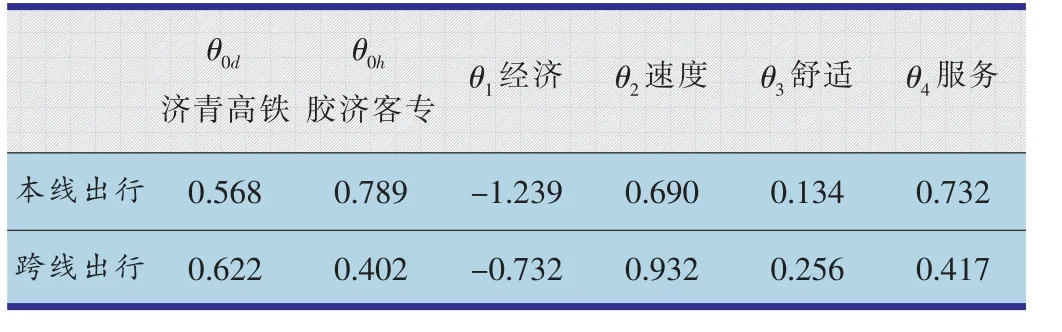
表1 胶济通道旅客出行效用参数

各指标及参数明确后，整理济青高铁与胶济客专的各有关数据，导入出行效用公式，即可得出胶济通道内本线旅客与跨线旅客的效用值，见表2所示。

表2 胶济通道旅客出行效用

3.2.2 博弈计算结果与分析

在输入本线与跨线旅客初始预测运量后，触发“计算线间博弈”开始对票价区间范围内的所有指标进行计算。竞争博弈同合作博弈的软件操作界面基本一致，因此仅对合作博弈界面展示如图1所示。

图1 计算界面（数据为计算中的随机数据）

触发“保存到Excel”，可将博弈计算过程及结果自动存储至Excel表格中，自动标注最大收益项。

根据区域铁路通道线间博弈系统计算得到合作与竞争博弈后结果数据，如表3所示。

表3 博弈前后的各项指标计算结果

由表3可得，通过竞争博弈，济青高铁与胶济客专的列车最优票价分别为125.6元和206.7元，济青高铁和胶济客专的总收益为426 491万元，提高3.09%。其中，济青高铁的收益273 789万元，上涨2.15%；胶济客专的收益152 702万元，上涨4.78%。

通过合作博弈，济青高铁与胶济客专的列车最优票价分别为148.8元和225.6元，济青高铁和胶济客专的总收益为445 139万元，提高7.15%。其中，济青高铁的收益304 613万元，上涨12.05%；胶济客专的收益140 526万元，下浮3.35%。

通过上述分析得到如下结论：

1）经过合作博弈和竞争博弈的验证可知，整个通道的收益均能实现增长，并且合作博弈获得到的效益高于竞争博弈所得，涨幅较博弈前是显著的。因此，在某一区域的铁路通道内若存在多线并行运营的情况下，高速线与城际线间推荐以合作博弈的方式有序运营、共享收益，有助于更好地提升运输企业的服务质量和经济效益。

2）目前山东省铁路网在济南和青岛间形成济青高铁、胶济客专和既有胶济铁路并存的“客货分离六线”运输格局，分工合理，各施其能。既有胶济铁路承担着通道内的货运功能，胶济客专以满足济南至青岛间的城际客流需求为主，济青高铁则以速度和时间优势承担区域对外客流交换功能，满足中长途旅客出行需求，实现了胶济通道内运力运能的优化配置，助力区域经济社会的高质量发展。

4 结语

利用博弈论解决区域铁路通道线间客流分配方法，旨在通过竞争或者协同发展的模式最大化铁路客运企业的经济效益。首先在充分分析国内外研究现状基础上，定义了本文研究的铁路客运产品设计为区域铁路通道线间客流分配，其次阐述了区域铁路通道旅客出行效用理论，并建立了基于博弈论的区域铁路通道线间客流分配模型，再次利用启发式算法对区域铁路通道线间客流分配模型进行求解，最后以胶济通道为例，借助C#2010程序语言设计研发了区域铁路通道线间博弈系统，自动计算并导出区域铁路通道竞争及协同发展模式下的各项客运收益指标，进而定量地确定了区域铁路通道不同线间的功能定位，为其他区域铁路通道建设提供较好的参考价值。