基于GPS/INS的自适应无迹Kalman滤波算法

曹红燕，刘长明，沈小林，牛兴龙，李大威，陈燕

(1.中北大学 电气与控制工程学院，山西 太原 030051；2.陆军装备部驻北京地区军事代表局某军代室，山西 太原 030051)

0 引 言

随着科技发展，军队建设对武器的作战能力提出了更高的要求。在无人机作战系统中，姿态信息获取及其测量精度作为关键因素，一定程度上决定着战争的成败，因此，需要选择更合适的组合导航系统，获得更高精度的姿态信息。运载体的飞行导航主要分为自主性导航和非自主性导航两种[1]，常用的导航系统有捷联惯性导航系统(INS)，全球定位导航系统(GPS)。INS导航系统[2]不依赖于外部信息，能够长时间持续工作，可在一定速度和时间内提供完善的导航信息，对姿态等信息的测量精度高且稳定性好，但测量误差会随时间越来越大，导致对姿态角等信息的测量精度降低[3]。GPS导航系统可以实时工作，测得更加完整有时序性的信息[4]，相比INS系统其在长时间连续工作时更加稳定，且精度更高。将GPS与INS系统结合构成组合导航系统，能够减小测量误差，弥补INS系统长时间工作精度降低的缺陷[5]，并能解决GPS系统信号失真问题，对姿态角，位置等重要姿态信息的测量具有更高的精度，更好的抗干扰性[6]。

目前国外对姿态信息测量的研究已有很多，如S.Bezick等[7]将Kalman滤波与外部非惯性导航系统相结合进行数据处理，提高了导弹导航系统的对准技术和精度；DENG Z[8]针对纯惯性导航模式下的周期振荡误差，设计了捷联惯性导航系统的外水平阻尼网络，提出了基于外速度的水平阻尼算法，通过三轴转台和仿真实验验证了该算法的有效性。文献[7-8]对于单导航系统进行算法分析，虽有一定改进，但没有针对组合导航系统进行算法分析与改进。H.E.Soken等[9]处理GPS/INS组合导航中的数据时引入Kalman滤波算法，取得一定效果，但如果GPS测量的数据出现粗差，姿态信息的测量精度将会受影响。目前已有很多研究针对导航系统的Kalman滤波算法进行了改进，涉及到扩展Kalman、容积Kalman、无迹Kalman等。在GPS/INS系统中，存在很多干扰因素，如系统模型扰动，噪声误差等，如果不考虑这些方面影响，组合导航系统将会产生测姿定位错误，带来非常恶劣的影响[10]。

本文在GPS与INS紧组合的情况下，利用四元数法对无人机轨迹进行测姿，对姿态角的信息运用扩展Kalman滤波、无迹Kalman滤波和改进的算法进行处理，并对比结果，分析实验数据。在无迹Kalman滤波基础上，提出改进算法，对数据进行最优估计和误差补偿。

1 基础知识

1.1 主要坐标系

姿态测量应用的牛顿力学是在惯性空间条件下确立的，尤其是在潜艇、炮弹、航空航天以及机器人领域应用十分广泛[11]。正确的坐标系对研究物体的运动非常关键，坐标系的选择会影响姿态信息的测量。本文仿真计算及试验涉及到的主要坐标系如下。

(1)惯性坐标系(oxiyizi)。此坐标系Zi轴沿地球自转轴极方向，xi,yi轴在赤道平面内，分别指向空间中的两颗恒星[12]。

(2)地球坐标系(oxeyeze)。xe轴与格林威治子午线对准，ye轴位于东经90°，ze轴与地球自转方向一致，坐标系相对地心惯性坐标系以ωe=15.041 088°/h的角速率旋转[13]，见图1。

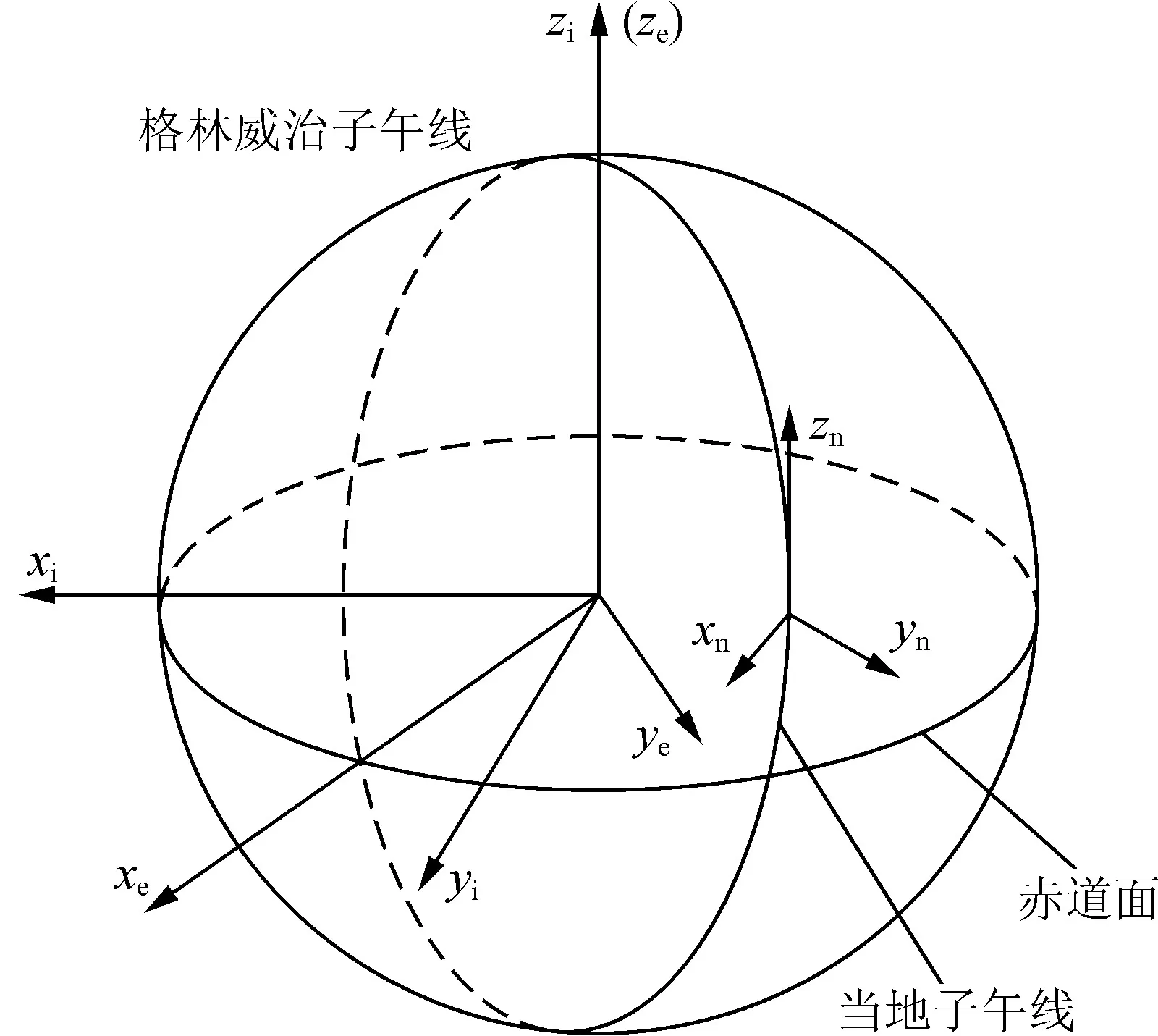
图1 地球坐标系

1.2 姿态角

导航坐标系(oxnynzn)经过三次旋转，可得载体坐标系(oxbybzb)，转换示意图见图2，转换后生成的姿态角说明如下。

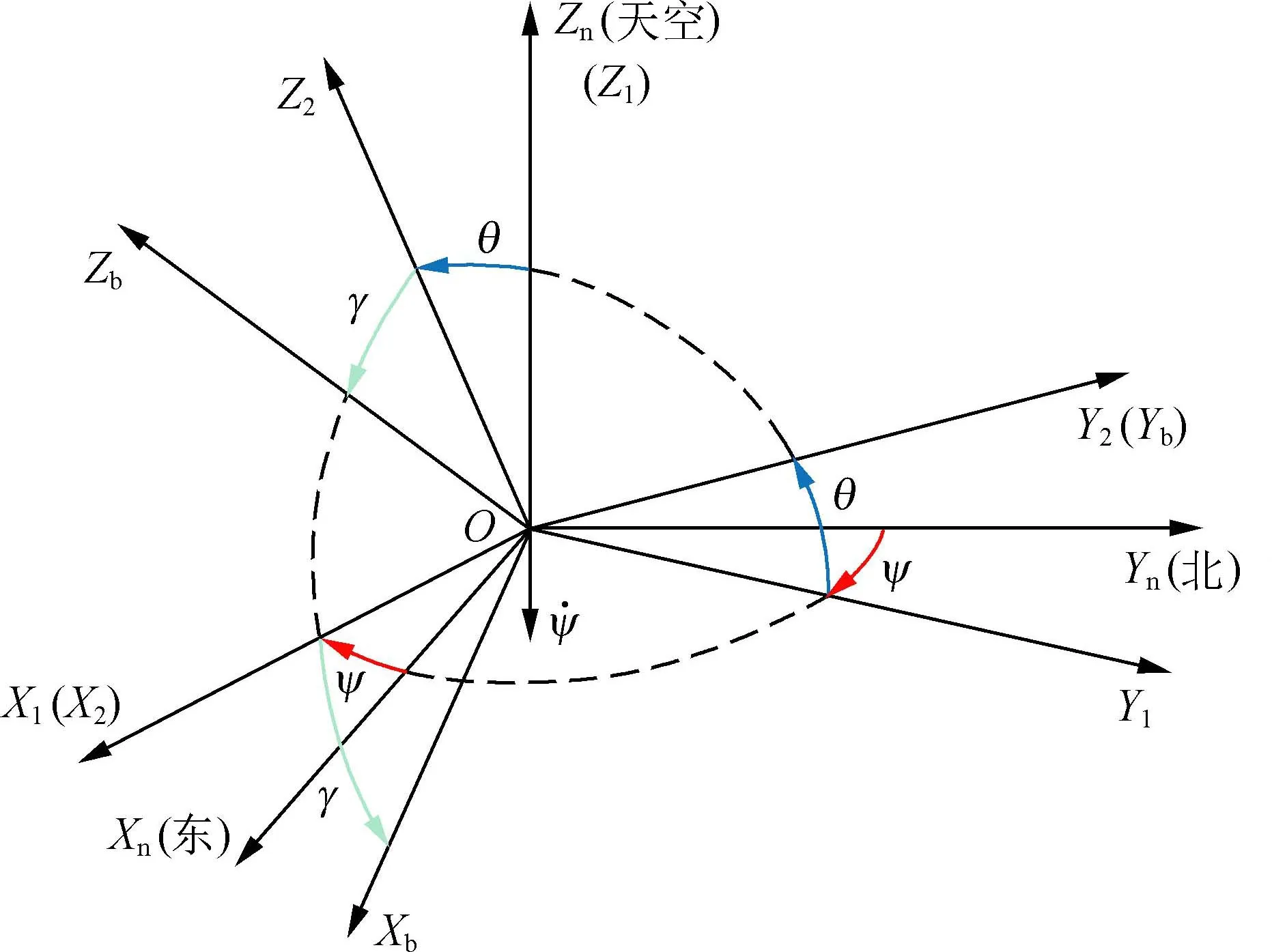
图2 导航坐标系与载体坐标系的转换示意

(1)航向角ψ。载体纵轴在水平面上的投影与地球经线的夹角[14]，[0°～+360°]。

(2)俯仰角θ。载体纵轴和水平面的夹角[15]，[-90°～+90°]。

(3)横滚角γ。载体横轴与水平面的夹角[15]，[-180°～+180°]。

本文对姿态角的更新测量采用四元数法，用四维向量的形式表示姿态信息，主要计算过程为

Q=q0+q1ib+q2jb+q3kb，

(1)

式中：q0，q1，q2，q3为实数；ib，jb，kb为载体方向的单位矢量。

四元数微分方程为

(2)

其中，ω=0+ωxib+ωyjb+ωzkb，可得矩阵形式，即

(3)

1.3 扩展Kalman滤波

扩展Kalman滤波是以Kalman滤波为基础的一种次优估计，利用泰勒级数展开非线性函数,并对高阶项采用忽略或逼近措施的近似线性化方法[16]，其中重要的计算过程如下。

非线性离散系统的状态方程和测量方程为

Xk=f(Xk-1)+Wk-1，

(4)

Zk=h(Xk)+Vk，

(5)

式中，Vk和Wk为高斯白噪声。

统计特性为

E[Wk]=qk，cov(Wk,Wj)=QkδkJ，

(6)

E[Vk]=γk，cov(Vk,Vj)=RkδkJ，

(7)

cov(Wk,Vj)=0。

(8)

初始状态X0独立于Wk，Vk，其中X0的均值和协方差分别为

(9)

P0=cov(X0，X0)=

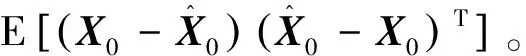
(10)

将Xk-1展开成泰勒级数并保留一阶项，

(11)

扩展Kalman滤波算法展开后仅保留泰勒展开式的一阶项，但高阶项也会对数据融合结果产生一定影响，可参考因素的减少会导致结果的片面性，因此，该滤波算法是非线性函数局部线性化的结果[17]，对于非线性化程度高的系统，随着时间推移，如果过程和测量噪声协方差估计不够准确，累积的误差会越来越大，测量精度越来越低，从而影响整个系统的工作。

1.4 无迹Kalman滤波

无迹变换是基于加权统计线性回归计算随机变量的后验分布[18]，无迹Kalman滤波融合算法是在无迹变换下进行近似线性最小方差估计的方法[19]，计算过程如图3所示，具体步骤如下。

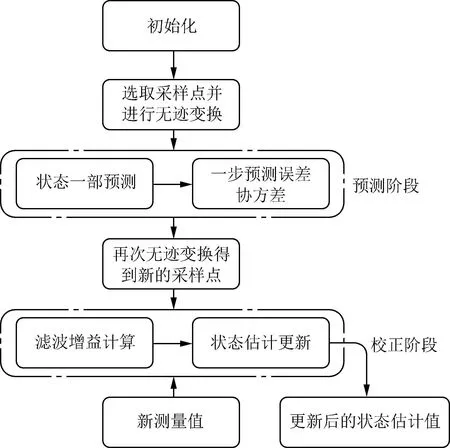
图3 无迹Kalman滤波计算过程

(1)初始化，初始状态为

(12)

(13)

i=1,2,…,n,

(14)

i=n+1,n+2,…,2n。

(15)

(3)对采样点集进行无迹变换，得到点集的预测方程为

Xi(k+1|k)=f(Xi(k|k),Wk)。

(16)

(4)进行加权处理，得到系统状态量的一步预测方程和协方差方程，分别为

(17)

(18)

(5)根据一步预测估计值再次进行无迹变换，生成新的采样点集，即

(19)

i=n+1,n+2，…，2n。

(20)

(6)根据非线性测量方程进行非线性变换，

Zi(k+1|k)=h(Xi(k+1|k),Vk)，

i=0,1，…，2n。

(21)

(7)进行加权求和并计算系统的测量预测值，

(22)

(8)计算协方差PXkZk及输出变量的方差矩阵PZkZk，

(23)

(24)

(9)计算Kalman增益矩阵，

Kk+1=PXkZkPZkZkT。

(25)

(10)状态更新：

(26)

P(k+1|k+1)=P(k+1|k)-

Kk+1PZkZkKk+1T。

(27)

Kalman滤波、扩展Kalman滤波以及无迹Kalman滤波3种算法各有优缺点，标准Kalman滤波假设系统状态和测量的数学模型是线性的，在线性系统中，能够有效降低噪声影响，但在实际工程中，真正意义上的线性系统并不存在，同时状态和噪声不一定符合高斯分布，所以标准Kalman滤波不适用于非线性系统。

无迹Kalman滤波计算非线性分布统计量的精度至少可以达到二阶，在特殊采样策略方法下能够达到更高阶的精度，在算法运算过程中模型没有损失，精度较高，所以本文选择无迹Kalman滤波算法进行主要研究，并将结果与前两种算法进行对比分析。虽然无迹Kalman滤波比Kalman滤波和扩展Kalman滤波有一定的优势，但仍会受到高斯噪声约束，如果涉及到复杂的待测数据，需要对算法进行改进。本文主要在GPS与INS紧组合的情况下进行试验，具体的流程图如图4所示，在该框架下对新息噪声，状态预测，统计量的阈值几个方面进行改进，验证并对比算法结果，流程图见图4。

图4 紧组合系统工作流程图

2 改进算法

2.1 新息噪声改进

在无迹Kalman滤波的变换中，sigma点集根据系统方程和测量方程计算状态估计和误差协方差阵，其中涉及到系统噪声和测量噪声的协方差阵Q′，R，这些噪声的状态属性值已知，均为预先设定的高斯白噪声，但是实际与理论的噪声不相符，Q′和R在算法运行中是实时变化的，存在一定偏差，随着时间累积容易造成滤波器的发散。针对这个问题，目前有学者提出了衰减记忆算法、模糊自适应算法等。衰减记忆算法主要引用衰减因子控制滤波器的发散，但测量精度大大降低。模糊自适应算法主要通过设定一个模糊推理系统预测噪声的方差值，适用于较弱的噪声，当噪声很强时，对数据的预处理较复杂。

为了解决此问题，本文的第一个改进是对系统噪声协方差Q′和测量噪声协方差R在线估值。观测新息矢量包括GPS位置、速度与校正后的INS位置、速度的差值，

eZk=Zk-HkXk|k-1。

(28)

计算最后N个观测新息的协方差，N为自适应窗口，取值可变，即

(29)

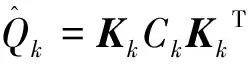
(30)

(31)

将式(30)和(31)分别代入式(18)和(24)中重新计算，在线估计噪声的统计特性，将系统噪声和测量噪声改进算法与导航系统融合。

2.2 状态预测改进

本文的第二个改进是对状态预测协方差矩阵引入次优渐消因子λk，改进后的无迹Kalman对状态预测协方差引入的次优渐消因子确定不需计算雅克比矩阵，具体计算过程如下。

(32)

(1)新息向量为

(33)

(2)次优渐消因子λk按式(35)求取，

(34)

(35)

(36)

(37)

(4)改进的状态测量预测协方差为

(38)

(5)对式(38)两边求迹，可得次优渐消因子：

(39)

(6)最后取值为

(40)

2.3 统计量阈值改进

(41)

图5 计算流程图

3 算法验证及结果分析

为了对比算法结果，验证有效性，本文将GPS系统和INS系统进行紧组合，在此框架下进行算法验证和MATLAB试验仿真，设计一段无人机飞行轨迹，计算陀螺仪和加速度计的数据信息，模拟各自的误差，与理想的惯性参数拟合在一起，解算出需要的姿态信息，利用本文所述的数据改进算法对数据进行处理，表1是本文试验的初始状态信息。

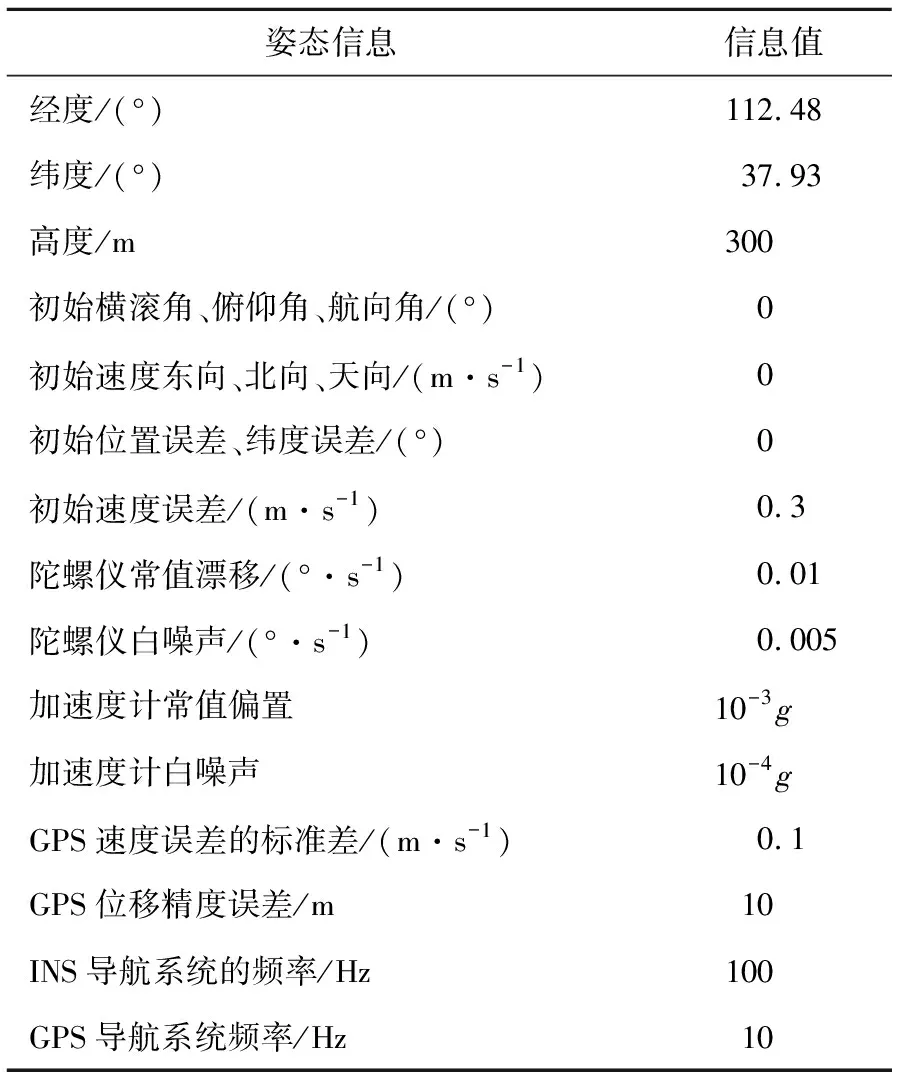
表1 初始状态

MATLAB仿真的无人机飞行航线轨迹如图6所示。

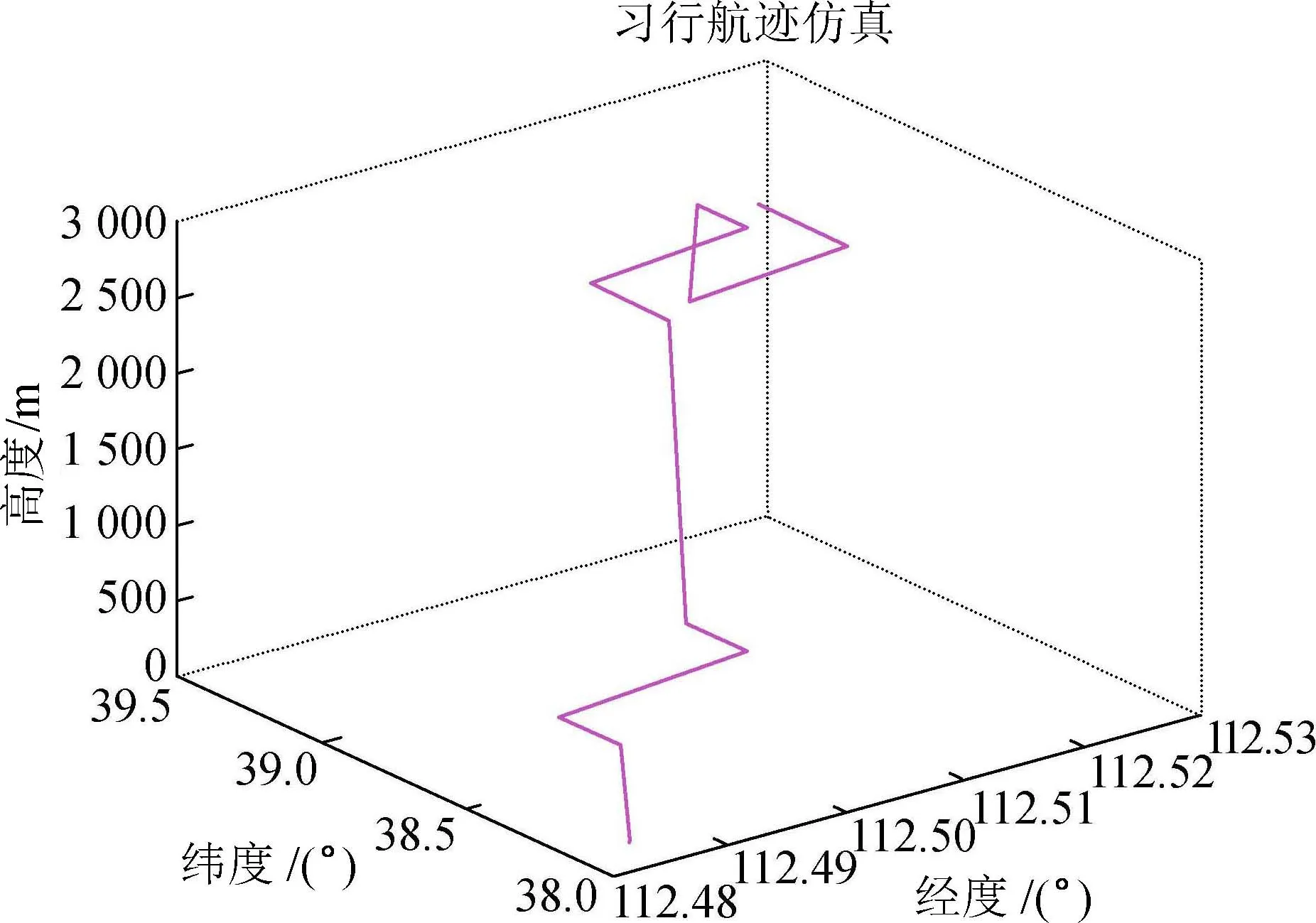
图6 总体航迹图

紧组合情况下，INS系统和 GPS系统互相独立工作，通过数据融合算法对其进行校正，图7～9是运用紧组合的导航模式对无人机姿态角进行测量并用扩展Kalman算法、无迹Kalman算法及改进的滤波算法处理数据的误差曲线。

由图7可知，紧组合导航系统测得的姿态角与真实姿态角的误差减小，俯仰角误差为-1°～6°，航向角误差为0°～6°，横滚角误差为-4.5°～0.5°。

图7 Kalman滤波算法补偿后姿态角的误差曲线

由图9可知，红色曲线为无迹Kalman滤波数据融合后的误差，黑色曲线为改进算法数据融合后的误差，两种算法都能将误差减小，比扩展Kal-man滤波后的精度高，在200 s左右姿态角绝对收敛，姿态角精度均高达0.1°，并在50 s之后绝对收敛，收敛性强于无迹Kalman算法，相比之下，改进后的算法抑制随时间漂移误差的能力更强，姿态角的精度更高。

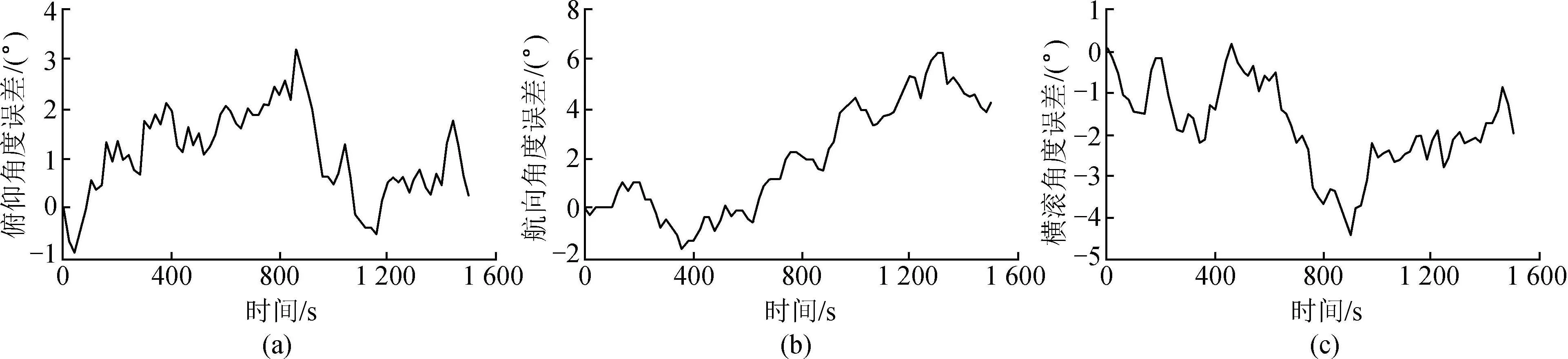
图8 扩展Kalman滤波补偿后姿态角的误差曲线

图9 无迹Kalman滤波及改进算法补偿后姿态角的误差曲线

4 结 语

使用常规Kalman滤波器对组合导航系统状态进行估计时，需先给定系统噪声和测量噪声的统计特性，但在实际物理过程中，无法确定噪声统计特性。针对此问题，本文提出了一种自适应无迹Kalman滤波算法，利用观测新息协方差对噪声统计特性在线估计，对状态预测引入渐消因子，重新计算状态值。以紧组合导航系统为背景，使得INS与GPS两个系统的优点缺点互补，满足了动态性能和抗干扰能力的需求，提升导航定位的精确性。运用3种滤波算法进行补偿分析，由结果可知，无迹Kalman和改进的算法测姿精度大于扩展Kalman滤波，有效抑制了INS系统误差随时间积累的现象，弥补了GPS的动态误差缺陷，本文的改进算法收敛性更强，稳定性更好，测姿精度更高，为了提高算法的实时性，保证算法的可用性，使算法具有说服力，未来会继续对算法进行改进，并将其应用于实物测试，获得更有效的数据。