高中数学：示“形”更揭“理”*——关于“刁尼秀斯之耳”的现象教学探索

费 峣 水菊芳

一、教学缘起

“刁尼秀斯之耳”讲述的是椭圆岩洞监狱中，犯人在焦点处（A点）的越狱谋划总会被位于另一焦点的守卫（B点）监听的故事。（图1）故事中的曲面反射现象是17世纪倒逼数学家研究曲线切线的重要问题之一，该现象的解决需要运用物理光学与数学知识，这决定了该故事中的现象有着较高的教学价值。然而，不少教师仅将其用于引入椭圆的概念，意在以故事的趣味性激发学生的学习兴趣。笔者以为，这种做法只提供了椭圆的“形”，却未能揭示椭圆的“理”，无法促成个体对现象的充分理解，也就无法创设利于数学核心素养生成的良好条件。由此，笔者想深度挖掘此教学素材，谈谈自己的教学探索。

图1 刁尼秀斯之耳

这里需要说明的是，以下的教学探索源于“现象教学”的理念，即依据真实现象，确定一些学习或研究的话题，并将之融入新的课程模块的教学。其教学要点在于提出某个现象，在教学中去探究它，并由此获得认识。基于此理念的教学更加凸显、关联真实世界，也更益于学生数学素养的生成。［1］

回到本教学内容，按照教材模块的编排顺序，学生在学习圆锥曲线时尚未学习导数的几何意义，对圆锥曲线的切线认识难触及实质。故此处教学定位为“圆锥曲线上某点处切线”的专题探究课，计划为两课时，分别设置导数几何意义（代数与图象）、椭圆光学性质（解析几何）两个探究话题，以实现跨模块知识融合纵深。以下为两个课时的主要教学内容。

二、导数几何意义

1.课时分析。

（1）教学内容分析：导数的几何意义是指曲线某点处切线的斜率。学生已经学习了平均变化率及其几何意义。此课时的目标是以此为生长点，从割线出发，用“无限逼近”的动态过程实现“局部以直代曲”，从而获得导数的几何意义。

（2）学情分析：初中阶段将“经过半径的一端（非圆心），且垂直于这条半径的直线”称为圆的切线。高中阶段则从几何与代数两个维度分别规定了直线与圆相切的位置关系，即“圆心到直线的距离等于半径”“直线方程与曲线方程联立有且只有一组解”。上述切线的静态理解可能形成思维定势，影响学生以直代曲思想的形成。

（3）教学重难点：初步的极限思想与局部以直代曲思想的生成。

（4）教学策略：利用信息技术动态演示，强化直观感知，以最原始客观的材料引导学生深入体会“无限逼近”与“量变到质变”，领悟“近似于精确”的哲学原理。

2.几何直观，按图索骥。

现象教学强调由直观感知到意义生成的学习过程，将之用于曲线切线的学习即为“建立形与数的联系，利用几何图形描述问题，借助几何直观理解问题，运用空间想象认识事物”。［2］学生对于切线斜率概念的完善、错误观念的矫正可以立足于小步调，由浅及深。

（1）鼓励想象：光线经椭圆一点反射与光线经直线上一点反射效果等价。

（2）模型优化：发动小组讨论得出（1）中所指的直线大概率为椭圆切线。

（3）概念蕴生：（1）中的“点”为切点，让学生隐约得到“椭圆上某点处切线”的初步感受，为导数几何意义的顺利发生做铺垫。

（4）试误与强化：教学中展示下列图象（图2），设计问题“下列图象中直线为曲线切线的是？”

（图2）

学生利用已有知识经验能成功做出A、B中直线为曲线切线的判定，对C则会犹豫但最终也会做出是切线的判断。但对于D则少有认可者，这就促使学生再度聚焦“刁尼秀斯之耳”的现象本身，明晰“曲线某点处切线”的数学严谨性，从而判定该图符合曲线切线特征。

【设计意图】本环节为现实情境的数学抽象，其抽象物为曲线切线，整个抽象过程需要学生逐步舍弃具体现象中的一切表象，学生借助空间想象，抽离出曲线切线在空间形式上的本质属性，主要培养学生直观想象与数学抽象的素养。

3.动态捕捉，数学实验。

教师充分肯定学生在上一环节中的表现，同时引导学生提出新问题，即“如何用数学刻画切线？”此问题的目的在于引导学生回顾“解析几何初步”一章直线的相关知识，进而想到用一个“点”与“倾斜程度”来刻画切线，以自我唤醒并强化旧知的方式，实现对所学内容的灵活运用。

此环节为“局部以直代曲”的教学，教师不应急切地给出形式化的定义，而应自然适度地提出问题，为学生提供问题解决的必要支持，如提示学生平均变化率及其几何意义，并以此为生长点，引导学生尝试对切线斜率进行深度思考。

（图3）

（表1）

【设计意图】本环节的目的在于促使学生通过对实验数据的分析，探寻客观现象的一般规律，在感悟数学推理规则的基础上提出有价值的数学结论，主要培养学生数据分析与逻辑推理的数学素养。

三、椭圆光学性质

1.课时分析。

（1）教学内容分析：椭圆光学性质指“从椭圆一个焦点发出的光线，经过椭圆反射，反射光线经过椭圆另一焦点”。该内容一般被视为阅读材料出现在各教材中，有益于学生综合运用数学知识认知客观世界，在高考考查中也有体现（如2013年山东理科卷题22）。

（2）学情分析：课时1的内容可以为本话题教学提供必要的知识储备，但由于考试导向、数学文化教育缺失、教师学科知识欠缺等因素，教材中阅读材料不被重视，学生鲜有机会对数学在实际问题中的应用做研究。

（3）教学重难点：现象的数学解释与推理论证。

（4）教学策略：精心组织探究教学，鼓励学生尝试多种信息渠道获得必要的研究资料、理论依据、工具手段，引导学生用数学方法解决物理问题，体验探究乐趣。

2.有据推理，现象释因。

（图4）

现象的解释需要规范的表达，并以此实现知识整体的结构化。探究“刁尼秀斯之耳”的光学性质需要相当的数学推理、演绎能力。教师可以根据所教学生的基础，酌情设计学生活动，实现不同学生数学能力的不同发展。

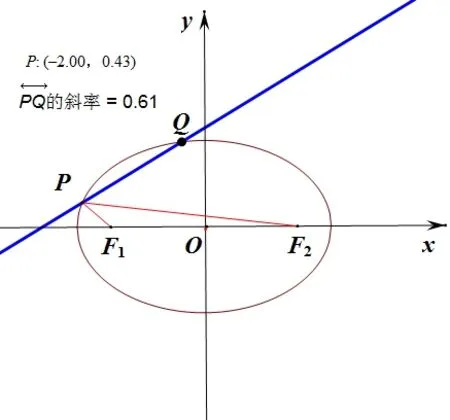
（1）方案设计，模型生成。学生借助平面直角坐标系，用解析几何模型来刻画现象，尝试表达数学问题，经历自然语言向符号语言发展的过程。此过程中，学生根据图4可以提出以下三种解决问题的方案：

（图5）

【设计意图】此处学生根据先前的分析构建数学模型并给出解决方案，采用数学运算的方式验证结果并评估建模的可行性，最终实现对现象的解释。本环节培养学生的数学建模与数学运算能力。

3.寓知于行，现象延伸。

利用网络、书籍等媒介带领学生回顾数学发展过程当中“无限逼近，以直代曲”思想的重要进程及典型案例，使学生置身于知识发生与发展的过程中，感受数学的人文情怀，实现学生的品格教育，践行立德树人的根本要求。让学生经受数学文化的熏陶、领悟数学美学价值的同时也务必警醒，数学文化在现象教学中的渗透不是点缀和花絮，需要在日常的教学中制定考察的方案、评价的标准。比如，学生通过椭圆曲面反射现象资料的研读，尝试撰写小论文、数学周记；再比如利用所学手段推导抛物线的光学性质，以数学沙龙的形式与同学分享成果。要让学生反思初窥数学现象时的不足，包括问题提出、数学猜想、方案设计、数学实验、合作探究等诸多方面的不足，也要让学生意识到自身的进步，意识到自身面对陌生的数学现象有勇攀高峰的可能，要让高远的数学观念与数学思想在学生看来“跳一跳，够得到”。

【设计意图】强化学生数学阅读，促进学生主动汲取知识，发展数学思维，培养学生终生学习的能力，实现数学文化的有效学习。

四、结束语

数学“形”与“理”的教学力求既能分析其代数意义，又能揭示其几何直观。此内容教学中，情境往往更直观，较为好用。但教师若错将重心放在情境创设的新、奇、巧、妙上，而对情境中与教学实质相关的内容不加挖掘，这就与数学教学的主旨谬之千里了。由此可见，情境不可能是世界本身，现象更接近于世界本身。［3］现象教学的理念否定了“情境引入”加“孤立于情境的教学”简单拼接的课堂教学模式，呼吁“回到问题本身”，既实现了学科价值的引领，又促进了学生理性思维的养成。

当然，现象教学在我国刚刚起步，仍有很多基础理论、实践案例有待研究。教师在教学中也不能崇拜模式，须知教无定法，贵在得法。教师在教学中应当批判吸收有助数学教学内容生长的材料，强化自身用好教学材料的能力，进而帮助学生构建更为科学的学科体系，提升学生的数学素养。