高背压进气道中内外流耦合作用的大涡模拟

王德鑫，褚佑彪，刘难生，李祝飞，杨基明

1.中国航天科技集团有限公司 第四研究院 第四十一所 固体火箭发动机燃烧、热结构与内流场国防科技重点实验室，西安 710025

2.中国科学技术大学 近代力学系，合肥 230027

吸气式高超声速发动机工作时，燃烧室背压会向上游传播，进而影响进气道/隔离段内部流动，诱使流场中产生激波串(Shock Train)[1]。在来流速度较高时，激波串可由正激波串发展为斜激波串[2-3]，同时剧烈的逆压梯度会诱导边界层分离，从而在激波串区域形成具有激波和湍流边界层分离的复杂流动现象[4]。通常，激波串会出现非定常振荡[5-6]，导致壁面产生脉动压力和热流载荷，易造成机体结构疲劳，降低飞行器寿命[3,7]。

激波串振荡问题涉及到激波与边界层相互作用，不仅流动复杂，且对下游背压扰动和上游来流扰动都极为敏感[1]。影响激波串特性有诸多因素，如流道长度[8]、侧壁面限制[9-10]、自激振荡[11-12]等。近年来，基于进气道模型研究激波串振荡问题已在试验和数值方法上得到一系列进展[4,13]。准确预测激波串振荡问题中的激波运动，还需更深入地理解背压扰动影响下的激波/边界层相互作用。对进气道出口背压扰动进行适当地简化，并借此来观测激波串的受迫振荡，是研究激波/边界层相互作用对背压扰动响应特性的常用手段[14-15]。在试验观测中，通过调节出口节流装置的变化幅度和周期，即可实现非定常背压出口条件。Bur等[16-17]通过试验研究了周期性背压作用下管道中激波串的非定常特性，较为精确地观测了激波和分离边界层的流动特征。Bruce和Babinsky[18]研究了频率为16～90 Hz范围内背压作用下的激波串振荡，发现激波/边界层干扰现象在激波向上游运动和向下游运动过程中明显不同。对于高马赫数情况，Wagner等[19]通过升降节流板，研究了来流马赫数为5、不同背压情况下激波串振荡时的激波移动速度。

尽管试验能够通过节流装置调控周期背压变化进而观察其对流场结构的影响，却难于观测流场下游背压处的振荡形式和传播机制。例如曹学斌和张堃元[20]在研究背压频率为2 Hz和4 Hz的激波串受迫振动特性时，发现壁面脉动压力主要与激波振荡有关。此外，具有激波串结构的内流道流动在固定堵塞度时也会产生振荡[21-22]。Li等[23]采用激波风洞试验研究了一系列固定堵塞度的进气道振荡问题，发现背压从下游向上游传播对激波串振荡的影响主要体现在增加激波串的平均速度和压力脉动强度上。Wang等[14]研究了激波串的自激振荡和受迫振荡，结果表明2种情况下的激波移动与下游堵块移动之间的时间延迟几乎一致，并得出下游背压向上游的传播速度接近于当地声速与流体速度之差。可见，固定堵塞比情况下，出口背压仍然会产生脉动，其作用可传播到激波串区域，而其中所涉及到的流动机理尚不明确。

相比于试验研究，数值模拟易于设定出口条件，如定常背压或脉动背压，实现激波串的自激振荡或受迫振荡。Su和Zhang[11]采用非定常雷诺平均Navier-Stokes(RANS)方法研究了不同背压下进气道内的激波运动，得到了不同定常背压下激波串的主要运动特征。Cheng[24]和Jiao[25]等对管道中的激波串振荡开展研究，发现低频背压下的激波串振荡更为剧烈。然而，激波振荡和湍流分离都具有多尺度特性，这使得RANS计算中设定的背压条件难以真实刻画试验中堵块处压力脉动的宽频特征。可见，压力脉动在激波串与堵块之间的传播难以通过RANS方法准确模拟[26-30]，相比之下，大涡模拟(LES)方法对流程的求解尺度更加精细，有望成为求解此类问题的有效手段。Krishnan等[31]对来流马赫数8下完全起动的进气道全构型进行了LES模拟。为使前体壁面流动充分发展为湍流边界层，Krishnan在计算中对前体壁面引入了吹吸扰动。Koo和Raman[32]采用LES方法对Wagner等[19]的试验进行了数值模拟，获得了精细的非定常激波结构，并将流道瞬时压力与试验结果进行了对比，发现在高堵塞度情况下LES 模拟获得的激波串向上游的传播速度较低。这些探索有效地获取了进气道的流动结构和脉动特征，为采用LES方法研究进气道激波串振荡问题提供了借鉴。

本文采用基于国家数值风洞(NNW)工程[33]流场软件的LES方法对典型堵塞度下的进气道进行全流场数值模拟，以获取非定常的流场信息。本文研究选用鼻锥钝化轴对称进气道模型，这可使流场免受侧壁影响，降低构型三维性对非定常流动的干扰。本文的目的是研究进气道内流道中的基本流场结构，揭示激波串与湍流分离的相互作用特征，深化对此类问题中流动机理的认识，这将对进气道工程设计起到理论指导作用。

1 进气道构型及数值模拟方法

1.1 进气道构型

本文研究选用鼻锥钝化轴对称进气道[34-36]，该进气道三维模型及截面形状见图1。图1(a)显示了轴对称三维模型[34]，图1(b)给出了模型周向截面参数[35]：捕获半径为64 mm；外压缩面总偏转角为 19.7°；内收缩比为1.58。进气道内压缩段采用高4.72 mm、长50 mm的水平喉道与下游长60 mm、单侧扩张角为1.9°的隔离段相连。试验研究中，为触发进气道隔离段的激波串现象，在隔离段出口采用节流装置，并以面积比TR衡量出口堵塞程度，对应计算公式为[36-37]

TR=(1-At/Ae)×100%

(1)

式中：At对应堵塞后隔离段出口面积；Ae为无堵塞时隔离段出口面积。本文计算的进气道模型出口堵塞比为50.8%。

试验在中国科学技术大学激波风洞 (KDJB330)中进行。来流马赫数Ma∞=5.9，总温T0=810 K，总压P0=1.27 MPa。基于来流条件定义的单位雷诺数为Re=4.7×106m-1。流场观测采用高速纹影拍摄结合瞬态压力测量。压力测量点如图1(b)所示，有CH1～CH13共13个测点。压力测量采用上海天沐NS-2型传感器，其最大响应频率约20 kHz。试验时压力信号的采样率为1 MHz。纹影拍摄与压力测量采用DG645信号延时器同步触发。

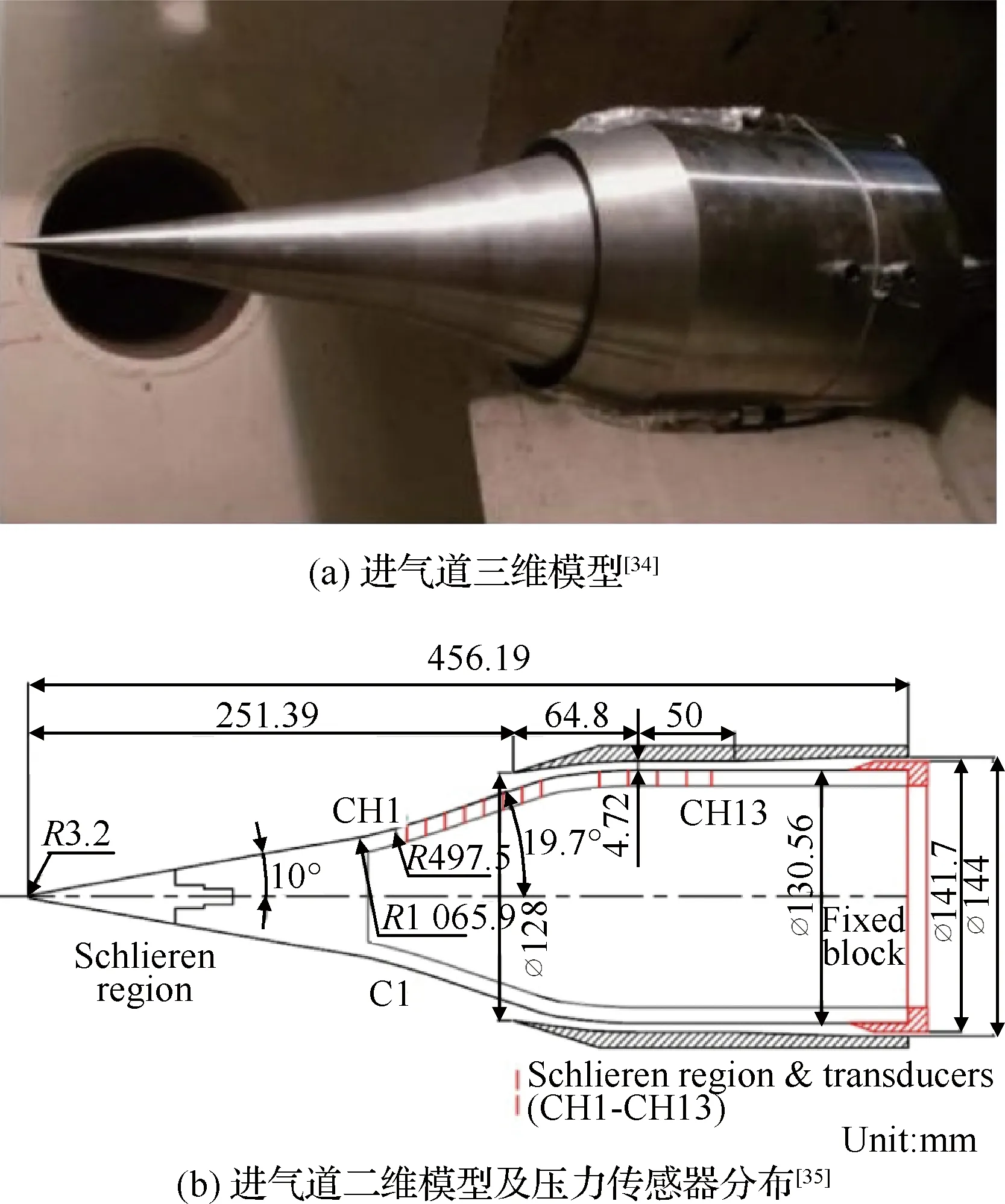
图1 轴对称进气道模型Fig.1 Axisymmetric inlet model

1.2 数值方法

本文数值模拟求解的控制方程为Favre滤波后的三维可压缩Navier-Stokes方程[38-41]，其形式为

(2)

(3)

(4)

式中：ρ为密度；ui为xi方向的速度；p为压力；τij为雷诺应力；Tij为温度；E为能量；qi为热通量；Ji为SGS湍流扩散项；Hi为SGS能量通量项；Qi为SGS黏性扩散项；σi为SGS应力张量分量；“-”和“～”皆表示滤波瞬时量，分别代表对变量进行空间滤波和密度加权Favre滤波；上标“SGS”表示亚格子(Subgrid Scale，SGS)项[38]。计算中对流通量使用Roe格式进行差分分裂，控制方程使用二阶迎风格式离散。流体为量热完全气体，分子黏性系数采用Sutherland公式计算，采用动力学亚格子湍流模型。计算参考量为无穷远处的来流参量，即密度ρ∞、温度T∞、声速a∞、压力p∞、以及隔离段水平喉道长度L。计算初始条件为无穷远来流参量。

为简化计算，本文计算域截取为试验构型周向(φ方向)的部分区域(约18°)，其余计算参数与试验研究[35]相同。计算中边界条件设置如图2所示：来流和法向远场取无穷远来流条件，壁面为绝热无滑移固壁，周向取周期性边界条件。为减弱出口扰动对隔离段流场可能产生的影响，在出口设置了缓冲区，详见图2局部放大图中的Domain 3。另外，为了确保气体流动在隔离段内发展为湍流，在前体壁面引入吹吸扰动[31,42]，扰动周期为0.5个无量纲时间。后验验证表明，在隔离段内湍流充分发展后，流场并未出现周期为0.5 的主导频率，这说明计算流场是符合物理的。

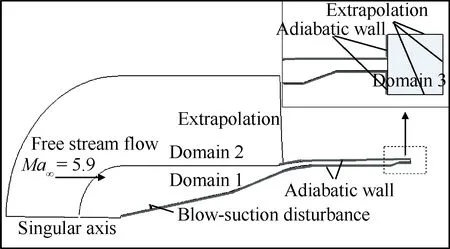
图2 计算域及边界条件Fig.2 Computational domain and boundary conditions

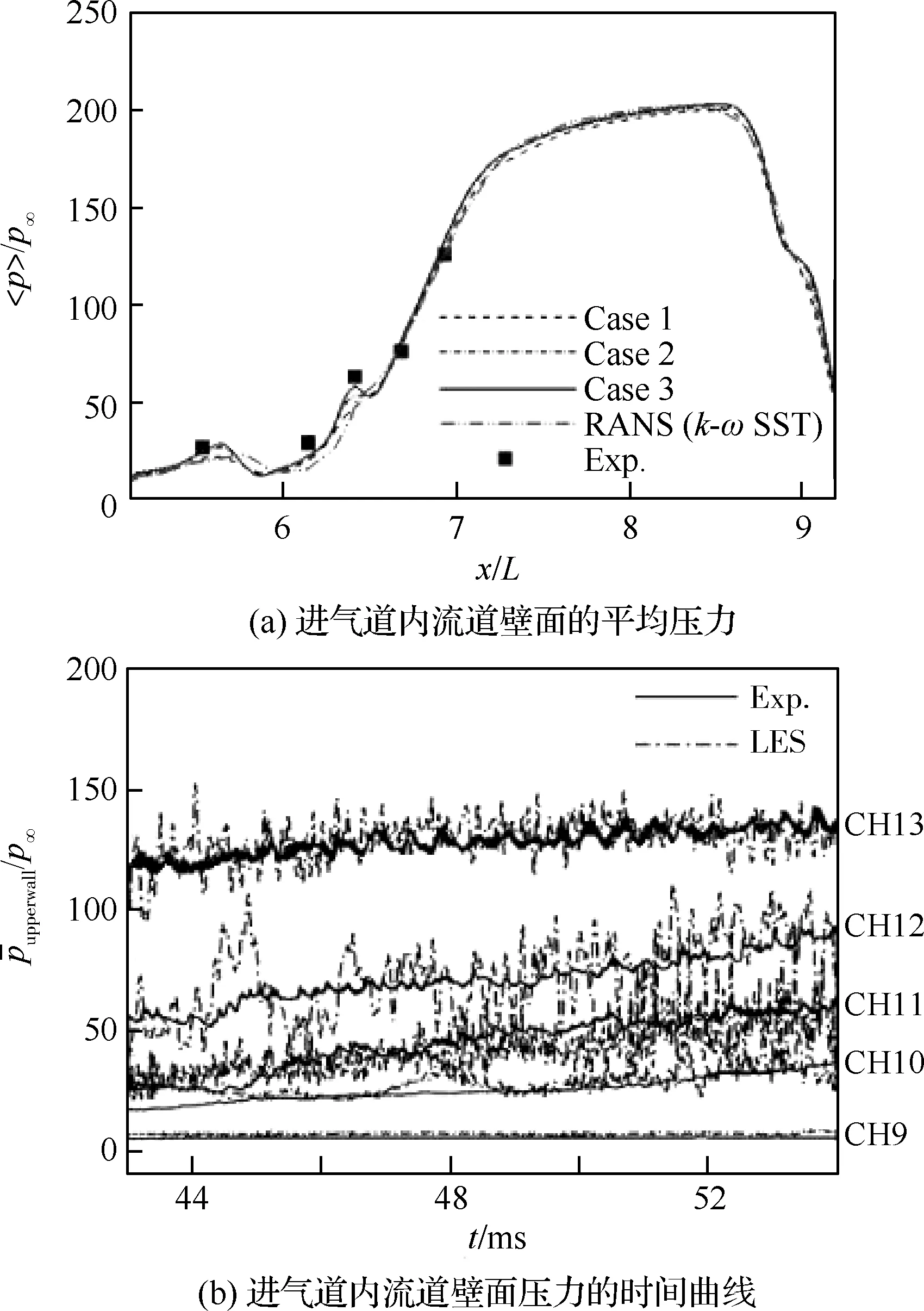
图3 大涡模拟计算结果与试验结果验证Fig.3 Validations of LES results with experimental data

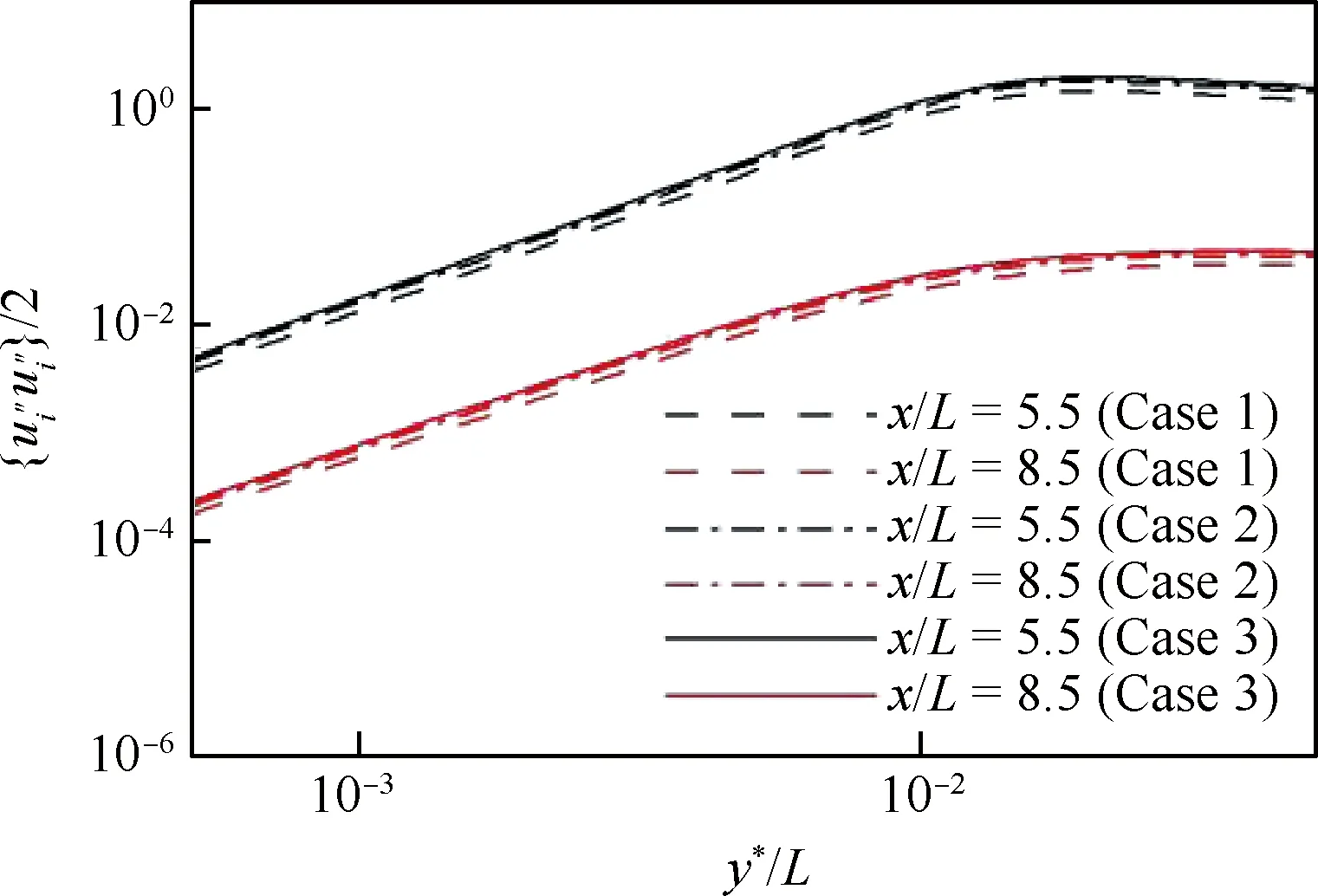
图4 湍动能统计收敛性Fig.4 Statistical convergence of turbulent kinetic energy

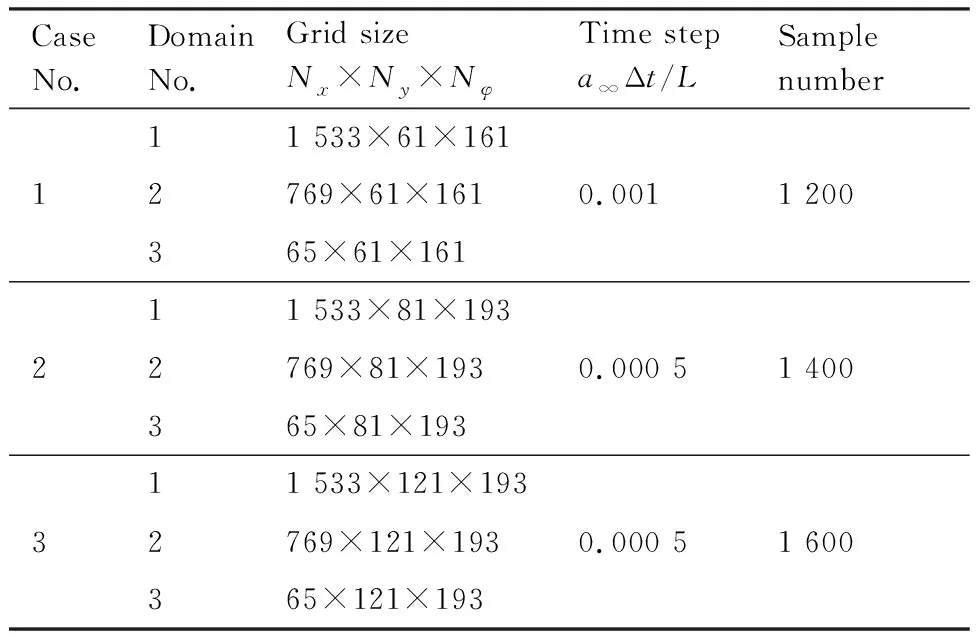
表1 计算网格数、时间设置及样本数

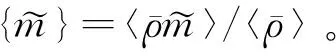
1.3 结果验证

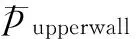
2 结果与讨论

2.1 进气道流场特征

高背压进气道流动具有上下游耦合特征，即同时受上游进气道外流场边界层湍流扰动和激波/边界层干扰、下游高背压引起的流场扰动的耦合影响[1]。为表征流场中大量存在的扰动涡结构，图5采用Q准则显示全流场涡结构分布。Q准则定义为

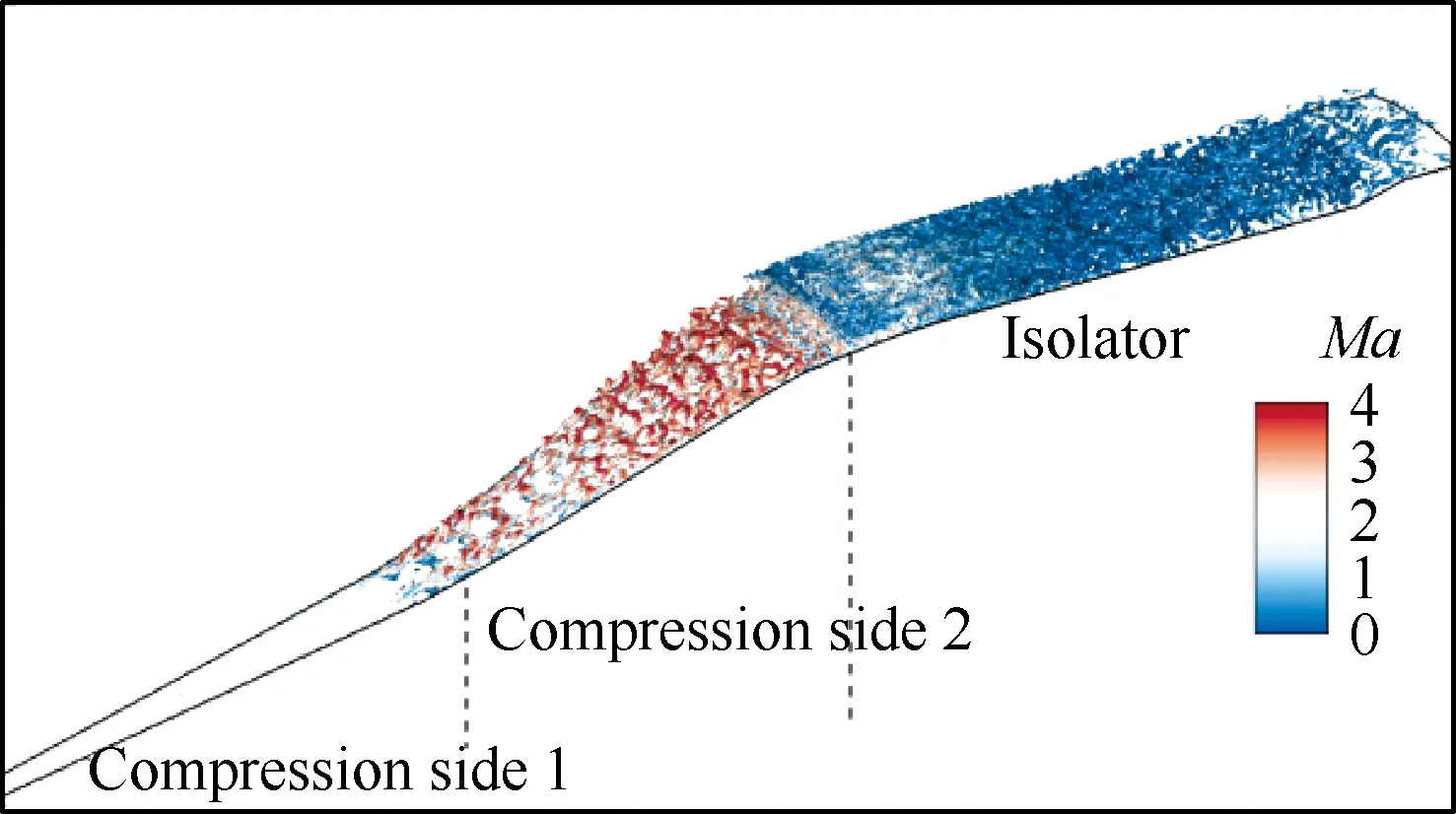
图5 Q准则表示的瞬时涡结构(以当地马赫数着色,Fig.5 Instantaneous vortical structures indicated by Q criterion (flooded by local Mach number,

(5)

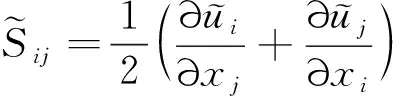
通过图5中涡结构分布可以看出：从进气道前体壁面一级压缩面与二级压缩面交界处开始，涡结构逐渐增多，壁面发卡涡在进入内流道之前得到充分发展，流动发展为湍流边界层。在隔离段下游堵块的影响下，出口附近气流汇集产生背压，导致气流速度下降，最终在隔离段内流道的中下游，气流由超声速流动转变为亚声速流动。从图5 给出的涡结构等值面上的马赫数可以看出，亚声速区域(Ma<1)出现在喉道区及其下游。随着下游背压向上游传播，为了匹配相应的压升，激波串在内流道中形成。同时，在内流道隔离段区，涡结构进一步增强，这表明由高背压产生的激波结构使得流场湍流强度明显增大，内流道中因而出现具有激波/激波和激波/边界层干扰的复杂流动。

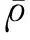
图6(c)显示了周向中心截面上瞬时流向速度(以当地声速进行无量纲化)的分布云图。与激波结构相对应，分离激波与壁面相互作用之后，诱导出边界层分离，其中下壁面上的分离尤为明显。IS 与下壁面作用之后产生闭合的分离泡(Separated Bubble 1)，背景波系与上壁面作用产生一个较小的分离泡(Separated Bubble 2)。在下壁面的激波串区出现了一段未封闭的大尺度分离区(Separated Region)，并形成分离剪切层(Separated Shear Layer，SSL)。分离剪切层在激波串作用下迅速失稳，脱涡演化为混合区(Mixing Layer，见图6(b))，产生成大量的涡结构，这与图5 中内流道中涡结构增强的区域相对应。

如上所述，全流场数值模拟结果显示，来自上游的湍流流动与下游的背压扰动在隔离段相互干扰。图7 给出了系综平均后的马赫数云图，其中下壁面附件红色线条为流线，黑色虚线为声速线。

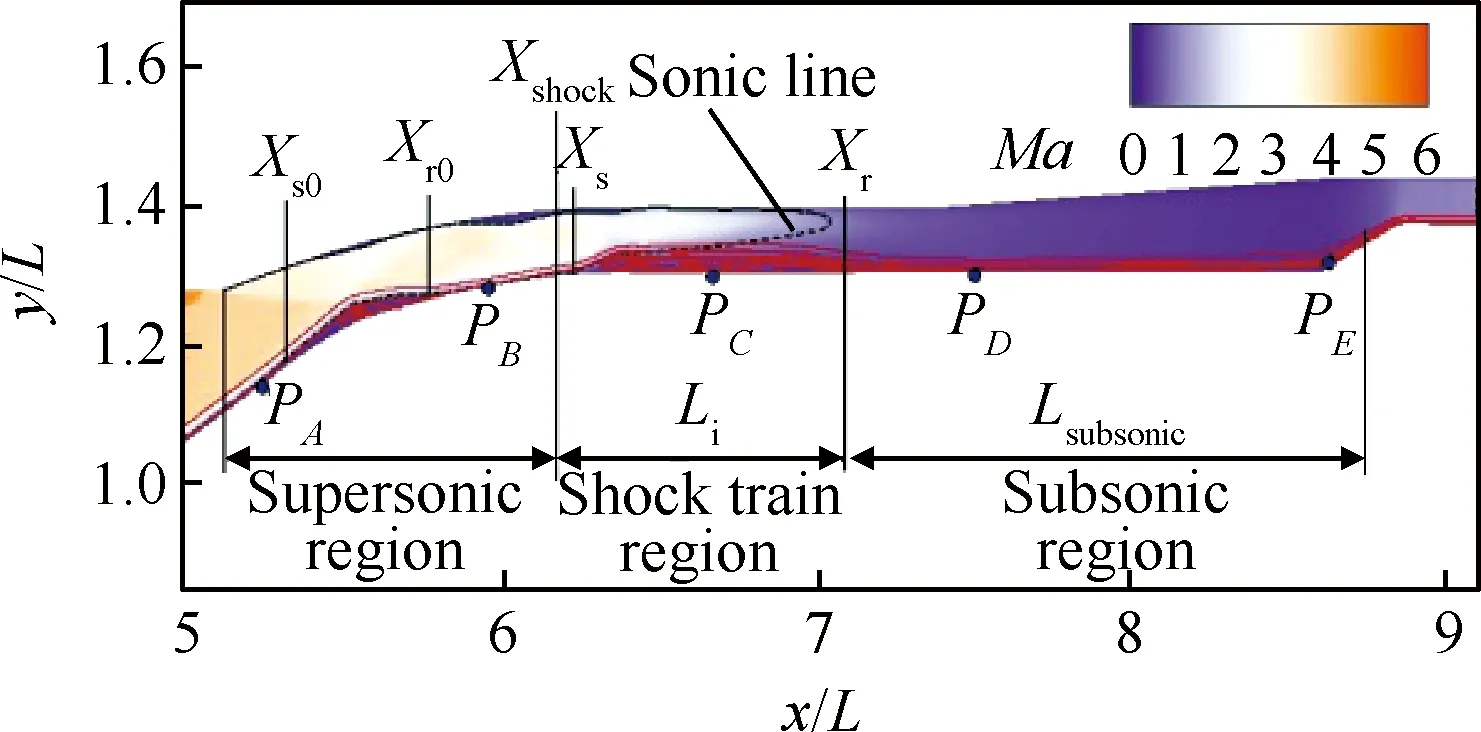
图7 平均流场马赫数云图及流线Fig.7 Averaged Mach number contours and streamlines

可以看出，根据平均流场马赫数分布云图可将内流道流场分为3个区域：

1) 超声速区(Supersonic Region)：从唇口到分离激波脚，主流区为超声速，流场分布着背景波系和封闭分离泡。

2) 亚声速区(Subsonic Region)：以声速线(Sonic Line)为界从分离区再附点到下游堵块，其长度Lsubsonic约为1.6L。

3) 激波串干扰区(Shock Train Region)：从分离激波脚到分离区再附点，长度Li约为L，主流超声速区分布着激波串，下壁面附近分离区流动为亚声速(以声速线为界)。

此外，图7中的流线分布显示，下壁面存在2处边界层分离：超声速区的分离泡，相应的分离点和再附点分别位于Xs0=5.40和Xr0=5.73；激波串区域的分离区，相应的分离点和再附点分别位于Xs=6.22和Xr=7.19。

复杂的流场结构导致喉道区出现较为严酷的压力载荷。图8(a)中的壁面压力分布显示：在喉道干扰区之前，上下壁面压力系数不到1；经过喉道干扰区，压力系数迅速上升；在干扰区下游，压力系数达到 8。

由于存在复杂激波结构，喉道和隔离段出现的压力载荷时伴有压力梯度的剧烈变化。图8(b) 给出了平均流向壁面压力梯度分布，其中流向压力梯度为正值时，为逆压梯度(APG)，流向压力梯度负值则对应为顺压梯度(FPG)。如图8(b) 所示，隔离段内流道流场主要以逆压梯度为主，且上下壁面因流动特征差异而出现压力梯度分布不同。在下壁面，分离激波位于x/L=6.2 处，导致该区域产生较强的逆压梯度，由于分离激波波后局部气流膨胀，压力梯度随之下降；之后因激波串的出现(x/L=6.4～7)，压力梯度再次上升，并随着激波串减弱逐渐下降。激波后区域内流动是以逆压梯度为主的，因而在下壁面诱导边界层分离。如图8(c)所示，下壁面上的强逆压梯度区对应于摩擦系数Cf为负的壁面分离区。对于上壁面，当分离激波在x/L=6.35附近与上壁面作用时，该区域出现较强逆压梯度，随后气流因波后局部膨胀出现顺压梯度，当到达干扰区的激波串附近(x/L=6.6～7)时，逆压梯度再次增强，随后因激波串减弱而逐渐下降。

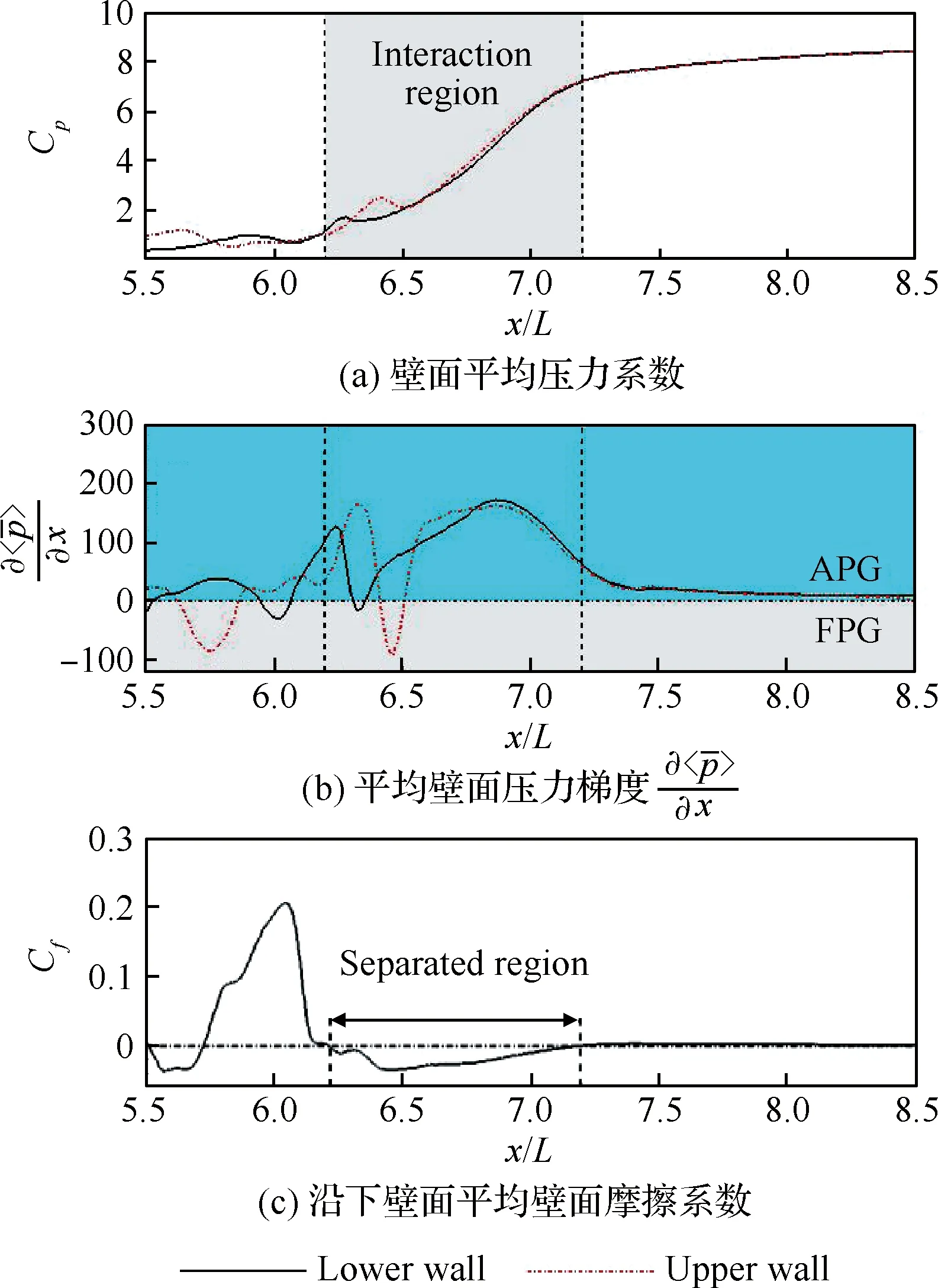
图8 壁面平均载荷特征Fig.8 Averaged load features on wall

2.2 流场非定常特征

在逆压梯度作用下，干扰区激波串与分离流动产生非定常运动，这使流场呈现显著的非定常特征。通过瞬时流场图像，可以清晰观察到干扰区的非定常流动[7]。图9给出了4个典型时刻瞬时流场数值纹影图，显示激波结构存在沿上下游方向的往复振荡；同时，干扰区激波与涡结构干扰产生大量脉动扰动，并向下游隔离段传播。如图9 所示，分离激波位置Xshock进一步显示了激波沿着喉道上下游方向的振荡特性。激波振荡范围约为0.2L，由t1=2.15L/a∞时刻开始逐渐向前运动，在t3=3.05L/a∞时刻到达最上游位置，随后快速向下游移动，在t4=3.25L/a∞时刻达到最下游位置，并进入下一轮的振荡循环。

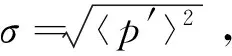
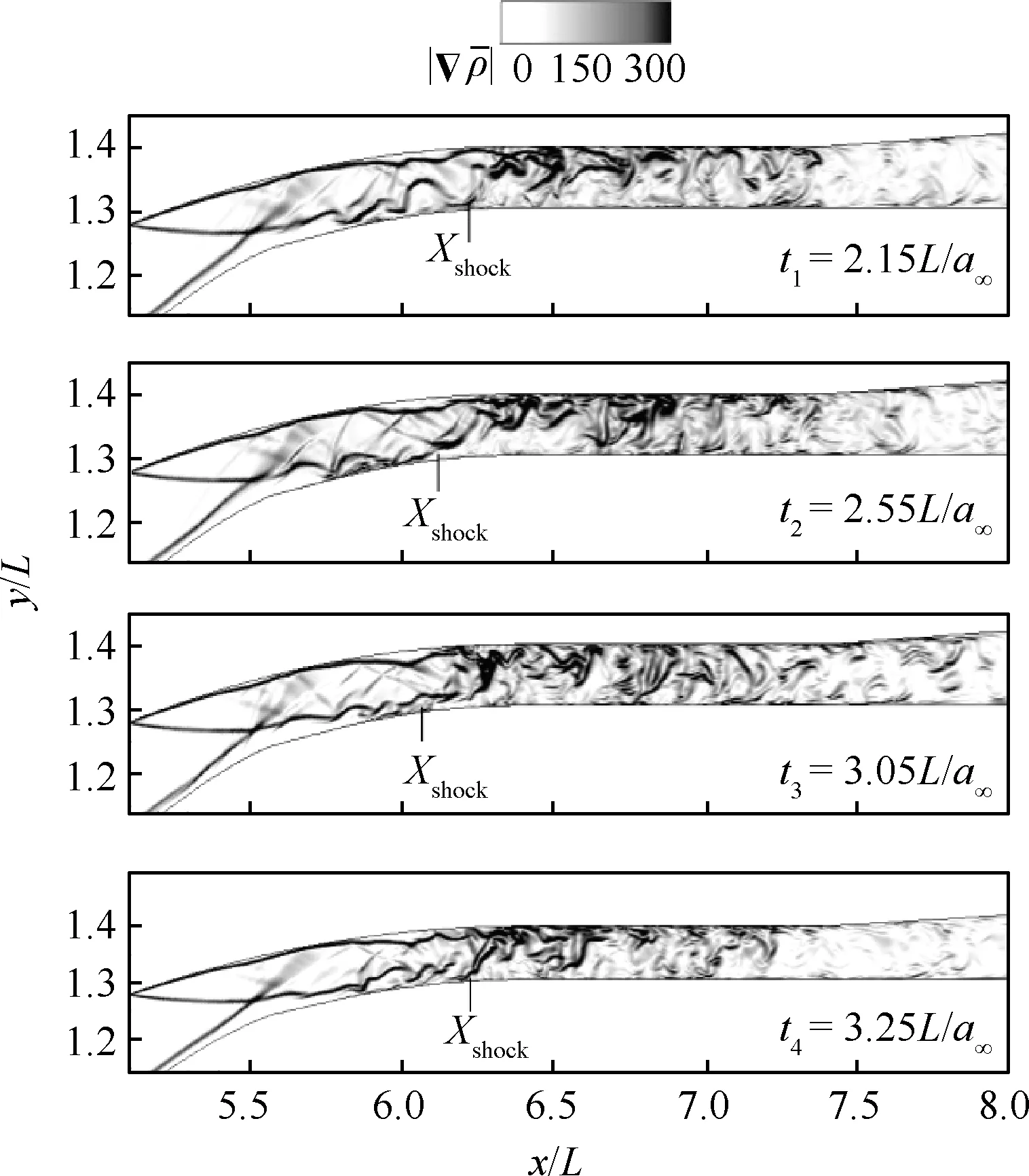
图9 φ= 0截面典型时刻瞬时流场数值纹影图Fig.9 Numerical schlieren contours of instantaneous flow field at typical moments on φ=0 plane

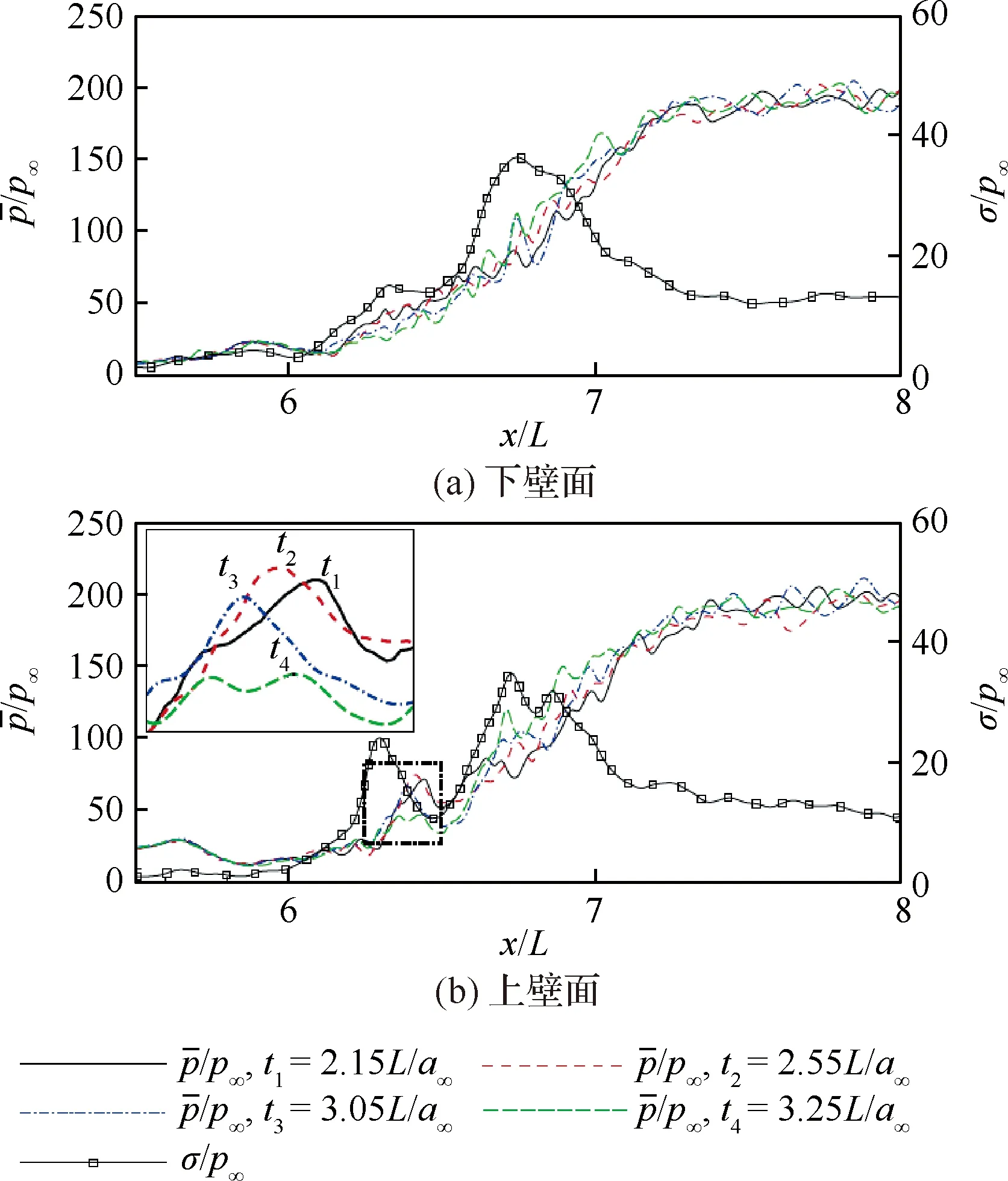
图10 上下壁面典型时刻的瞬时压力以及压力脉动均方根沿流向的分布Fig.10 Distributions of instantaneous pressure and mean square root of pressure pulsation on upper and lower walls along flow direction at typical moments

壁面压力的频谱信号有助于进一步分析流场的非定常特性。表征频率的无量纲量为St=fa∞/L(其中f为压力频率)，采用功率谱密度函数(Power Spectral Density, PSD)描述脉动压力均方根σ在频域上的分布特性[43]。图11给出了下壁面5个测点PA～PE(分布位置见图7)的压力脉动PSD。如图11所示，进气道内流道的压力脉动具有宽频特征，且主导频率与测点附近的流场演化特性相关。5个测点压力频谱均有高于St=10的高频分布，这一频率与湍流边界层特征频率(O(U/δ)，U为流场主流平均速度，δ为边界层厚度)相近，表明进气道内流道的湍流已充分发展[44]。PB位于入口封闭分离泡下游，该处出现一个较弱的低频St=0.7，说明此处的激波系存在非定常运动，其频率远低于来流湍流边界层特征频率。PC～PE分布于激波串干扰区及下游亚声速区，具有比较明显的低频St=0.9(约为3.6 kHz)，低频St=0.7出现。

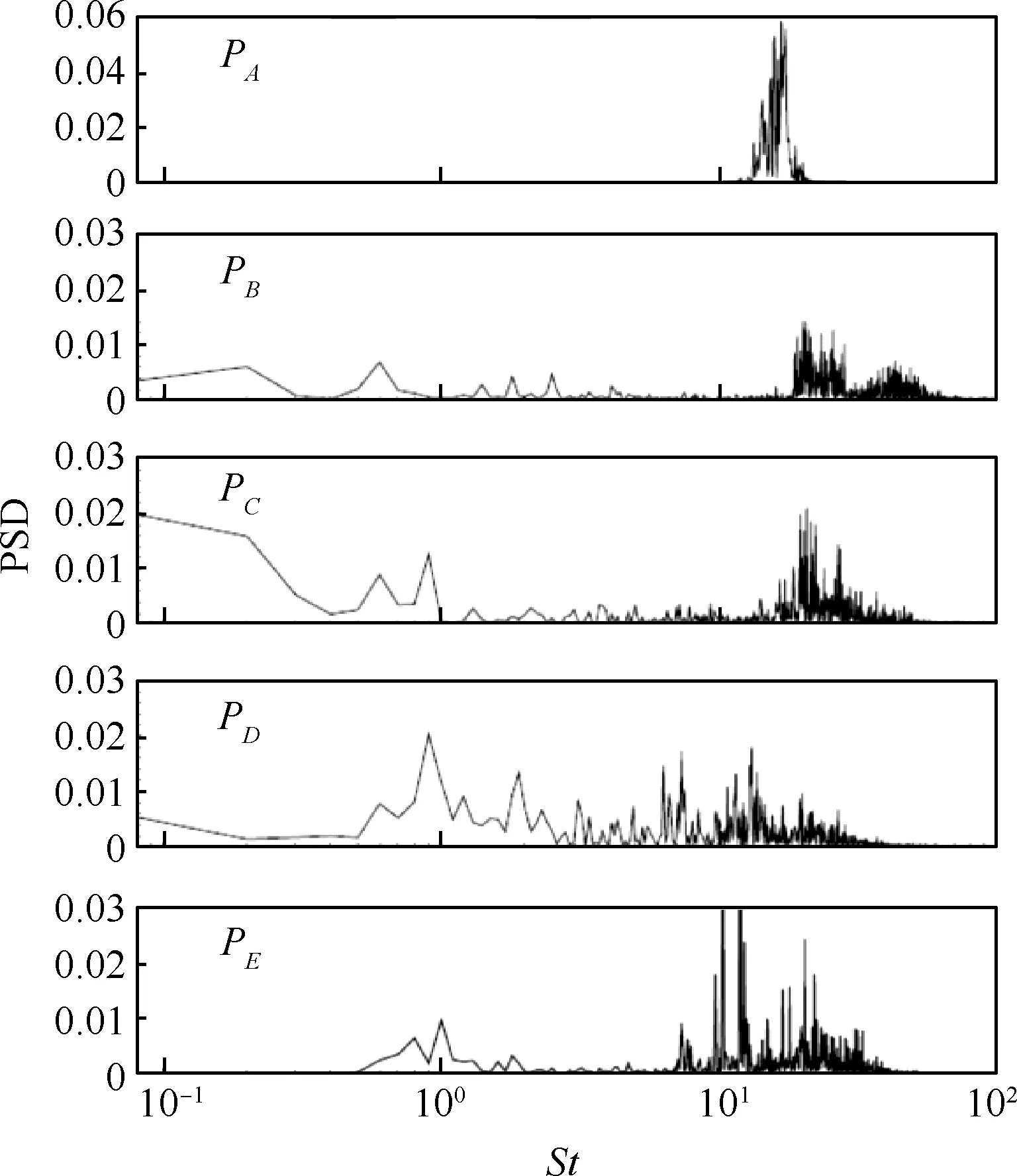
图11 隔离段内壁面压力频谱分布Fig.11 Pressure spectrum distribution on inner wall of isolator

由图10可知，在分离激波运动范围内，激波波后局部压力随激波串移动而变化。激波向上移动时，波后压力上升，反之则波后压力下降。

图11表明，低频脉动压力出现在分离激波下游的所有区域，而非局限于波后局部区域。为探讨激波串下游流场对激波串振荡的影响，需要获得内流道全流场的脉动压力信息。图12给出了进气道内部上下壁面脉动压力的时空分布，其中横坐标为空间位置，纵坐标为时间轴，云图为脉动压力。从图12中可以看出：在亚声速区(x/L=7.2～8.8)，上下壁面压力脉动的分布呈现黑白相间条纹状，表明壁面压力随流场振荡出现正负相间的脉动。如图中红色箭头所示，脉动压力的条纹分布形状表明压力脉动以扰动的形式自上游向下游传播。同时还可以看到，压力脉动能够沿着绿色箭头从下游传播到激波串区域。压力脉动的这一分布特征，与Trapier等[29]在研究进气道喘振问题时发现的流动扰动传播机制类似：亚声速流场扰动以声速传播到上游激波处，引起激波运动。

图12 流场壁面脉动压力时空分布Fig.12 Temporal and spatial distributions of fluctuating pressure on wall of flow field

对于进气道/隔离段流动问题，Trapier等[29]研究认为脉动压力传播的速度是当地声速，流动速度是小于声速的，因此压力扰动形成一种声共振形式的自维持振荡。对此，Newsome[26]采用声反馈模型较好地预测了脉动压力自维持振荡的频率，模型为

(6)

式中：Lsubsonic为反馈区域长度；cloc为亚声速区的平均声速；Mam为亚声速区的平均马赫数。根据上文计算结果，Lsubsonic取为1.6L，cloc取2.71a∞，Mam取为0.49，此时反馈模型可以表示为Stn= 0.32(2n+ 1)。当n=1时，预测频率为0.96，与上文亚声速区的低频St=0.9符合较好。这表明激波串区的脉动源于下游内流道的不稳定性，即压力扰动在亚声速区沿流向来回传播导致的振荡特性。

2.3 激波串干扰区脉动机制

通过对壁面脉动压力时空分布以及声反馈模型分析显示，干扰区激波结构的振荡具有周期性，且频率与内流道主流速度对应的时间尺度接近。激波与边界层相互作用问题一般会存在一个比湍流边界层特征频率(O(U/δ))低1～2个量级的低频(O(0.01U/δ～0.1U/δ))[45-50]。同时背压作用下的激波与边界层干扰流动涉及到多种流动结构的耦合作用。

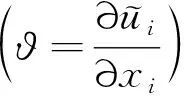
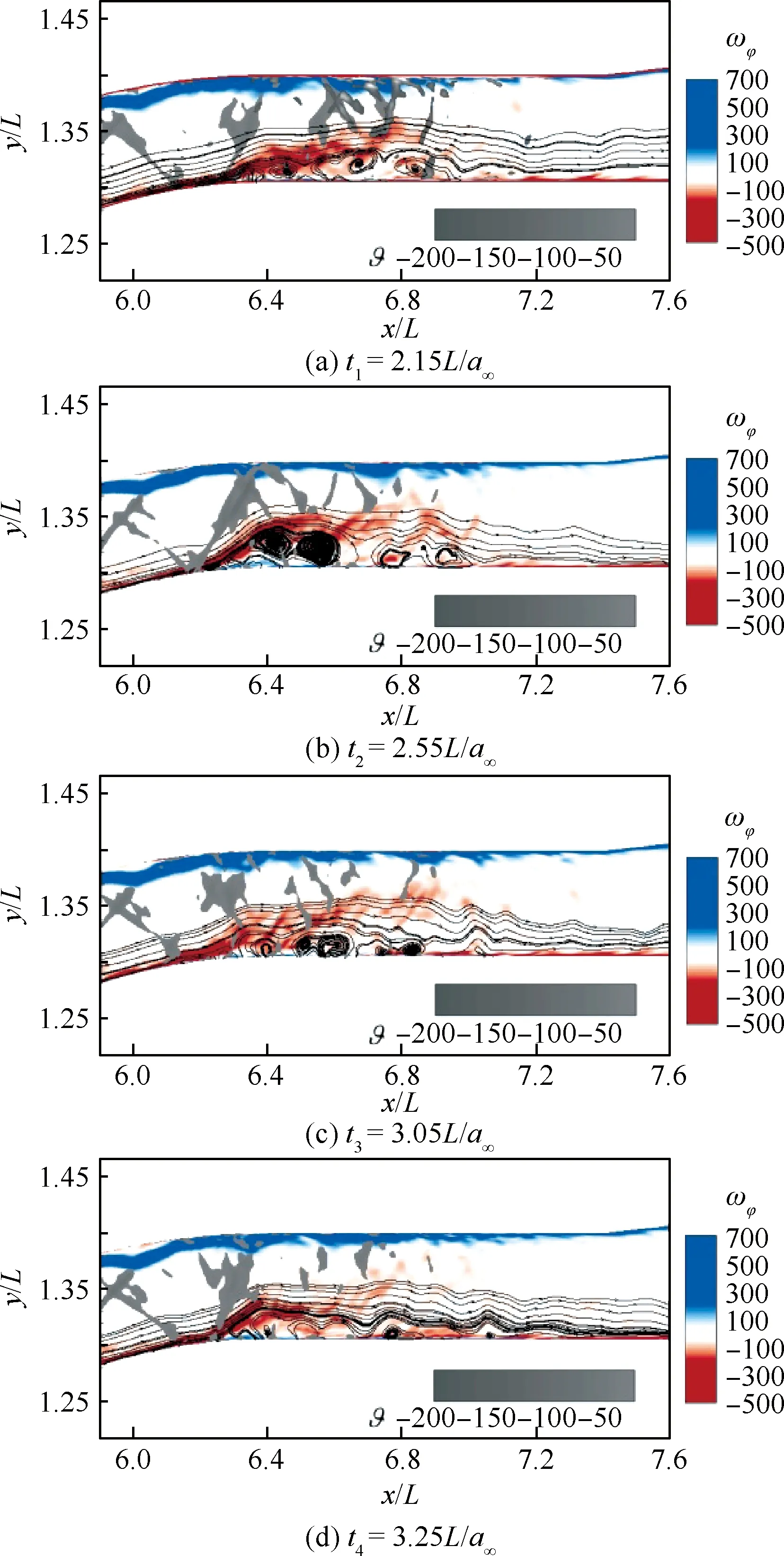
图13 φ= 0截面典型时刻干扰区的瞬时流场Fig.13 Instantaneous flow field of interference region at typical moments on φ=0 plane

由于分离区尺度较大，激波和剪切层结构的振荡运动高度耦合。结合瞬态流场分析可知，激波结构向上游运动时，分离区尺度增大，反之则分离区尺度减小。这里采用分离泡高度h描述分离泡的大小，h的定义满足：

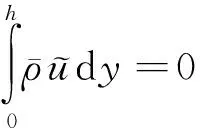
(7)

通过对样本流场的h做统计，可以得到其概率分布。图14(a)给出了分离区高度的统计概率。从图中可以看出，分离区高度最小为0.014L，表明分离区一直是存在的。h的整体分布显示中等高度的概率最大。

图14(b)同时显示了基于h的概率分布做条件平均所得的流动分离区范围。作为典型情况，将对应于h最小的流场样本做条件平均，得到分离区最小(Thin)情况下的条件平均流场，类似可得中等分离区(Medium)和最大分离区(Thick)情况下的条件平均流场。从图中可以清晰地看出分离区的膨胀收缩特征，分离区高度与主流的通过宽度、激波串的挤压程度密切相关。

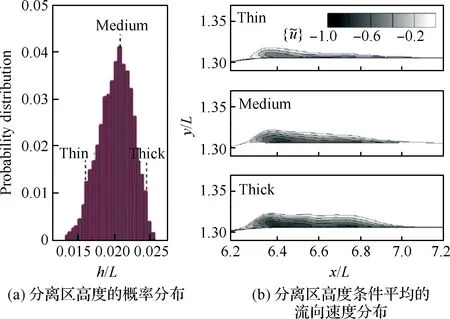
图14 分离区高度的概率分布及其条件平均Fig.14 Probability distribution of separated region height and conditional averaging of separated region

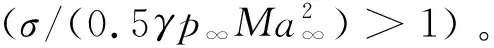
考虑到流场的非定常振荡特性，图15对比了3种分离区下的脉动压力均方根。可以看到，在激波串与上壁面干扰处，流场振荡对壁面载荷影响最为剧烈。相比于分离区减小、激波串向下游振荡，分离区增大、激波串向上游振荡时的上壁面脉动压力要高出约20%，这说明内流道干扰区的流场振荡对壁面脉动压力载荷具有显著影响。

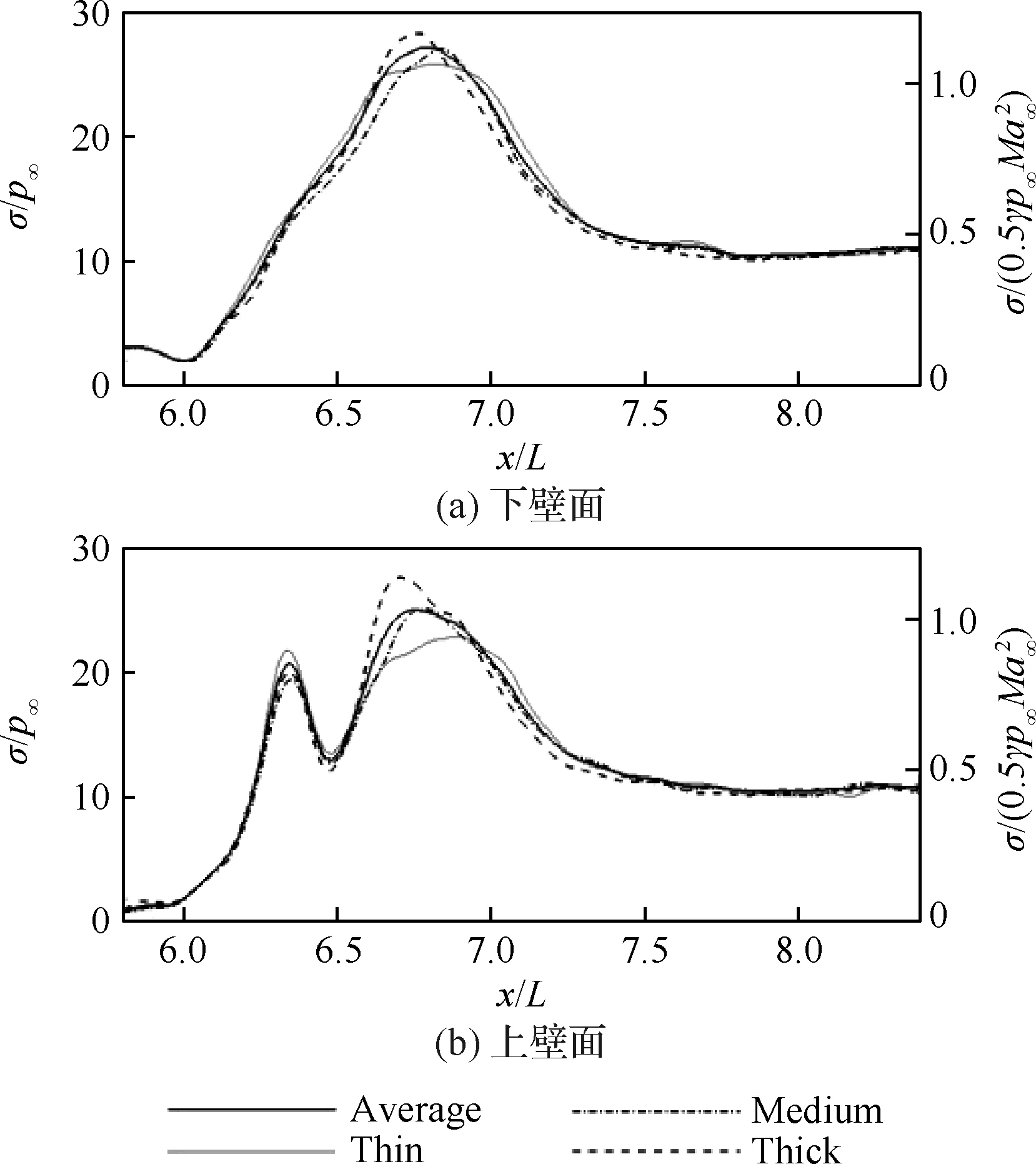
图15 压力脉动均方根沿上下壁面的分布Fig.15 Root mean square distribution of pressure fluctuation along upper and lower walls

由图14分析可知，激波运动与流动分离关系密切[50]。为此，考察流场中分离流动最为强烈的2处区域，即下壁面的分离泡和分离区。图16(a)给出上游分离泡的分离点和再附点的瞬时位置，图16(b)给出喉道分离区的分离点和再附点瞬时位置以及分离激波脚位置。图16(a)和图16(b)显示，尽管上游的分离泡和喉道的分离区均发生非定常运动，但是运动规律并不相同。图16(c)和图16(d) 给出了这5个量的PSD分布，结果显示，Xs0主要呈现小尺度的脉动，其频谱集中在St=10附近，与来流湍流边界层脉动相关。Xr0具有小尺度高频脉动，同时还包含St=0.7的运动。图16(d) 显示，Xs，Xr，Xshock的主导频率为St=0.9，并具有St=0.7的特征。

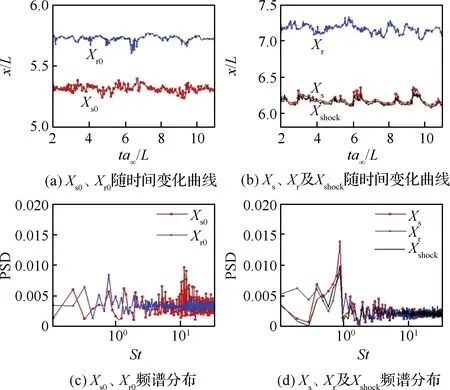
图16 下壁面附近分离泡及分离区的非定常特征Fig.16 Unsteady characteristics of separation bubble and separation area near lower wall

为了定量讨论分离区振荡扰动的传导机制，如图17所示，对分离激波脚(Xshock)、分离区分离点(Xs)和再附点(Xr)的横坐标做了时间相干性分析。其中，时间关联系数定义为

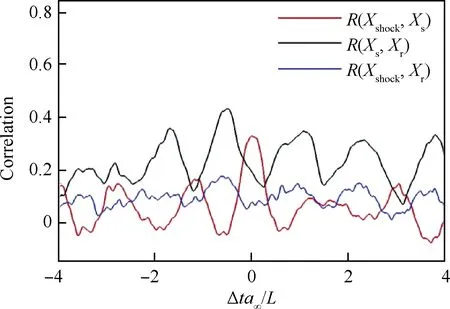
图17 Xs、 Xr、 Xshock之间的时间相干性分析Fig.17 Temporal correlation analysis of Xs, Xr, Xshock

R(r1,r2)=〈r′1(t)r′2(t+τ)〉/(σr1σr2)

(8)

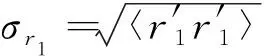
为了进一步讨论激波非定常运动与上下游流场的关系，图18给出了Xshock与PA～PE这5个典型位置压力信号时间相干性。Xshock与PA～PE分别代表了激波、终点与堵块处信息。从图中Xshock与PA的时间相关性分析可以看出，位于激波串区上游与激波串区之间的压力相关性较弱，对应的频率主要集中在高频段，表明激波串的高频振荡与上游而来的湍流有关。图中Xshock与PB的时间相关性分析显示：频率为St=0.7的激波结构的低频振荡与上游相关，即位于x/L=5.4～5.73的分离泡。Xshock与PC～PE的时间相关性分析表明，分离激波与下游压力信号呈现负相关，说明下游压力上升时，激波串往上游移动，此时下游扰动在激波结构运动中占主导作用；同时通过相关性的频谱特性可以看出：位于激波串区下游与激波串区之间的压力相关性对应的主频为St=0.9，表明由下游扰动的主导振荡频率为St=0.9。

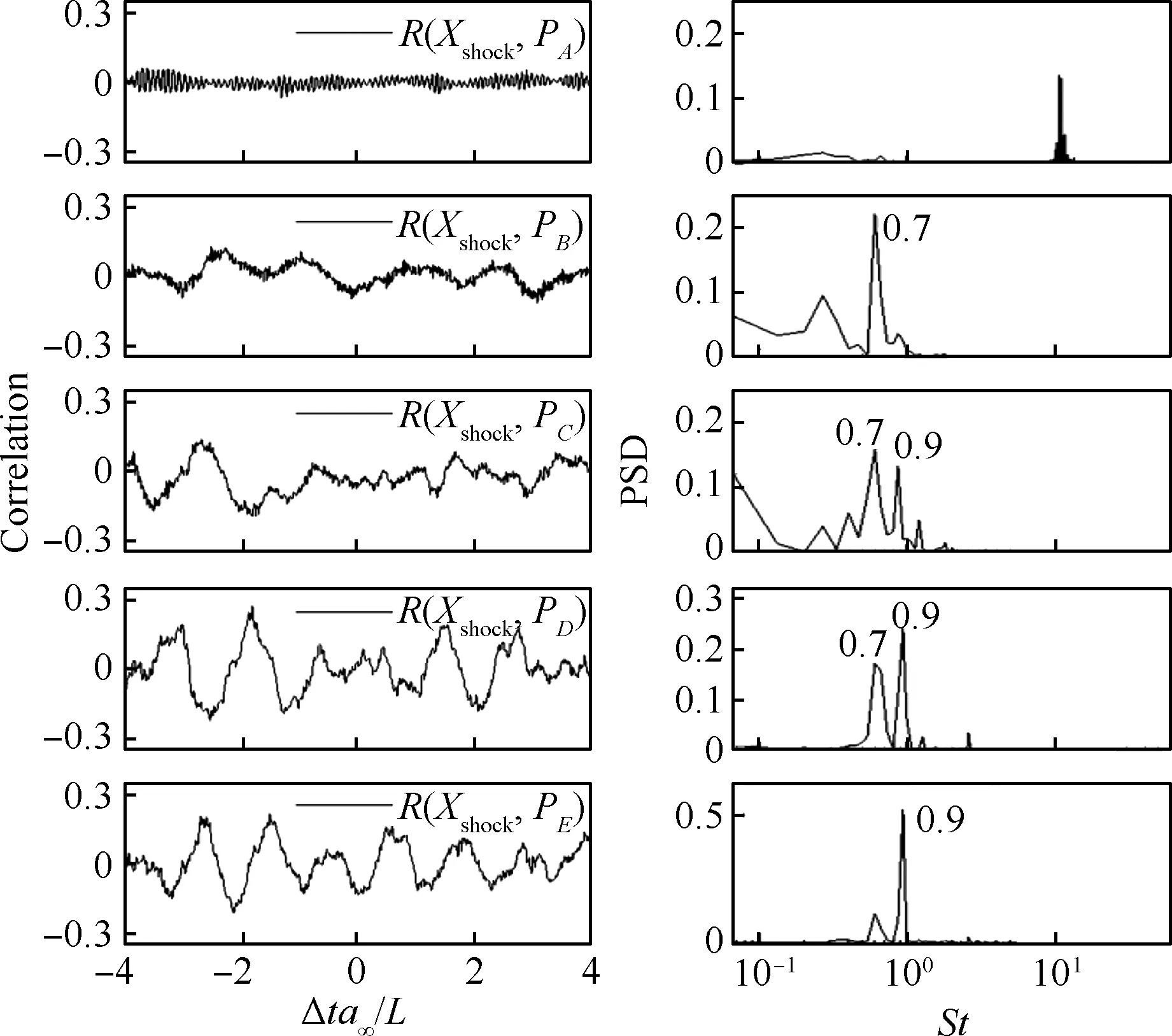
图18 Xshock与PA ～PE的时间相干性分析及其频谱特性Fig.18 Temporal correlation analysis of Xshock and PA-PE and spectral characteristic of correlations

3 结 论

本文采用大涡模拟方法研究了出口堵塞比为50.8% 的进气道内外流耦合流动中激波串的非定常振荡特性。基于对轴对称进气道模型的三维流场模拟，分析了这一复杂流动中的流体力学基础问题，如激波与分离区相互作用，上下游耦合引起的流动振荡机制等。本文主要结论如下：

1) 为匹配出口背压，流动在进气道等直隔离段区形成激波串结构，导致流场分为上游超声速区、中部激波串区以及下游亚声速区。在高背压的作用下，激波串区形成剧烈的逆压梯度，使得边界层发生大尺度分离，从而形成分离激波、激波串、分离区以及分离剪切层等一系列复杂结构。

2) 伴随着激波串运动和边界层大尺度分离，激波结构出现非定常运动。整个流道均出现与湍流边界层特征频率相近的高频压力脉动；上游分离泡产生St=0.7的低频脉动，分离区和亚声速区出现St=0.9的低频脉动。内流道脉动压力以扰动波的形式传播，为此建立的反馈模型可较好地预测亚声速区脉动压力的主导频率，即St= 0.9。

3) 瞬时流场分析表明，当下游压力扰动传到激波串区时，分离区挤压隆起致使剪切层上摆；随后分离点前移，导致分离激波脚前移；随着压力扰动的衰减，分离点后移，剪切层下摆，分离区坍缩，激波串区被挤压，分离激波后移。利用条件平均分析发现，分离区处于坍缩状态时，流场激波强度下降，壁面脉动压力较低；而分离区鼓起时，激波强度上升，壁面脉动压力均方根上升约20%。非定常相关性分析表明，激波串运动受上下游耦合作用，其中，频率为St=0.7的运动主要受上游湍流边界层影响，而频率为St=0.9的运动主要受下游压力扰动波影响。