异质零件的静态建模方法

杨继全，李 娜，施建平，唐文来，张 钢

(南京师范大学电气与自动化工程学院，江苏 南京 210023)

传统的CAD模型侧重于零件的几何及空间拓扑描述，零件通常认为由单一、均匀材料组成。与传统的CAD建模方法不同，异质零件建模将零件的材料种类及分布作为新的设计变量，通过合理地设计产品的几何参数及材料的空间组分分布来实现特殊的产品设计要求。同时，异质零件建模可充分发挥多种材料的优点和特色，产生新的复杂结构和功能，因而在诸多领域将得到广泛应用。异质零件建模的核心是将产品的几何结构与材料设计有机结合起来，使用统一的格式或转化接口，使几何结构特征和材料组成有机地整合为一体，直接用于数字化制造生产。

近年来，针对材料均匀、规律变化的静态建模方法研究较多，本文给出基于体素法和基于边界表示法的结构模型，并把材料信息添加到结构模型中，设计异质零件的静态模型。点云数据是三维建模常见的数据存储方式，基于空间点云数据的建模具有通用性。本文基于点云数据选择特征节点，使用赋予材料属性的方式实现异质零件模型的数字化定义，采用不同色彩表示不同材料，实现异质零件模型建立的可视化。

1 静态模型

在现有的异质零件模型建模方法中，较具有代表性的有基于体素法的建模方法和基于边界表示(boundary representation, B-Rep)法的建模方法，静态建模方法是指在三维物体结构建模的基础上，加入材料信息及映射方法的建模方法。

1) 基于体素法的异质零件建模。

体素(voxel)，是体积元素(volume pixel)的简称，是数字数据于三维空间分割上的最小单位。

Siu等[1]提出了基于“梯度源”的建模方法。梯度源可视为零件内部材料的“发源地”，以任何一个固定参考如点、线、面为梯度源，距离函数f(d)作为材料组分的分布方程，d表示模型内某点到梯度源的距离。定义一个n维的数组N存储异质零件内各点的材料组分信息。f(d)和数组N作为从异质零件几何空间映射到其材料空间的依据。对于材料分布较为复杂的异质零件，该方法难以满足材料的建模需求。

吴晓军等提出了距离场定义下的CAD建模方法[2]和基于欧氏距离测度网格模型体素化算法[3]。前者是一种基于固定参考特征和活动梯度源的方法，后者是利用线性八叉树的编码特性，将三维多边形网格模型离散成体素表示的模型，通过多边形网格轮廓体素和模型内、外体素序列的标志位特性，将三维网格模型内部体素化，产生准确的26-邻接体素模型。此种采用体素的建模方法，易于表达材料分布不规则的非均匀实体,但是只能以有限的分辨率逼近真实实体，准确性低,为精确表达实体，需要大量的存储空间。

Jackson等[4]提出了利用有限元网格描述零件几何信息，用内部有限元单元节点到边界的距离为变量表示材料信息的建模方法。该方法采用材料局部组分控制模型，基于有限元网格描述异质零件几何信息，以内部有限元网格节点到边界的距离为变量描述材料信息。该方法对异质零件的描述用公式(1)表示。该方法的不足之处在于模型被细化为不规则的四面体单元，数据运算和切片分层等数据处理较为复杂。

(1)

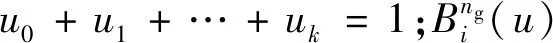
2) 基于B-Rep的异质零件建模方法。

Kumar等[5]以B-Rep为基础，采用以描述异质零件模型外形的rm-set集合与描述材料变化信息的rm集合相结合的方式进行异质零件建模，用几何空间描述异质零件几何信息，用材料空间描述异质零件材料信息。该建模方法采用rm-set和建立在正则集上的正则布尔运算，明确异质零件在几何与拓扑特征上的非流形特性，根据异质零件材料信息部分的特征，将异质零件几何区域剖分成有限个互不相交的正则几何区域，各个子区域的并集形成完整的零件几何区域。在零件的材料信息表述上，对于单个点的材料特征模型，假设异质零件的材料种类数目为n，以各种构成材料的体积分数表示零件内任意一点上的材料特性，并且每个点上的各材料组分的体积分数之和恒为1。

其材料空间V用式(2)表示：

(2)

式中：‖·‖1表示L1-norm(即绝对值相加，又称曼哈顿距离)；v为模型各个剖分区域的材料空间；Rn为整个模型的材料空间；vi为第i个材料体分量。

其几何空间E3到材料空间Rn的材料映射函数为：

(3)

式中：F为材料函数；x为模型的几何剖分区域。此种rm-set模型的缺点是只能表示简单的材料分布，且材料分布的表达依赖于坐标系。

Kou等[6-7]提出了基于B-Rep的建模方法和异质特征树(heterogeneous feature tree, HFT)建模方法。其几何空间的表述建立在B-Rep基础上。在材料信息表达上，HFT由一些安排有序的节点组成，每个节点由子节点组成。不同层次级别节点的材料变化有相互依存关系，高层次级别节点的材料组成由它的子节点材料和每个子节点材料的权因子共同决定。这样通过树形结构将实体材料空间变化的依存关系进行编码，在进行材料组分查询时，通过相应的“解码”实现材料组分的动态查询。此种异质特征树方法可以描述多种材料分布，但是用户无法预知模型的结构、热力和其他性能。

此外，Patil等[8]提出了采用R函数描述材料结构的建模方法，他们采用rm目标模型描述异质零件模型；Biswas等[9]提出了基于几何域的场建模方法；Huang等[10]研究了基于三维像素点的建模方法和基于空间曲线控制点的建模方法，并对异质零件有限元分析和成形方法进行了研究。

这些建模方法较为复杂，多停留在理论研究阶段，大都未能基于目前广泛采用的商用CAD软件和STL模型进行材料信息的表达，且与后续异质零件的成形方法没有充分结合起来[11]。本文设计的具有材料特征的彩色微四面体建模方法力图解决这些问题。异质零件的数字化模型设计流程如图1所示。

图1 异质零件的数字化模型设计流程

2 网络节点的获取

采用STL文件描述基于空间点云数据的异质零件建模方法，通过三维造型软件画出异质零件CAD三维模型，保存为便于读取的ASCII码形式，进而获得STL格式的文本文件，读取文本文件便可获得三维坐标，得到几何空间结构，再把材料域建立在空间域的基础之上[12]。本节重点描述的网络节点是材料模型的基本单位。

2.1 外轮廓几何表示及STL模型细化

采用通用STL格式表示的三维模型如图2(a)所示，仅能从几何表示角度来描述模型，该描述方式的优点是对规则模型的描述简洁高效，有利于数据存储及运算。但对于曲面较复杂或精度要求较高的模型，这种描述方法的数据冗余度较高、数据量大、精确度较差，且多种软件输出的STL数据存在一定差异，从而导致表述的零件模型存在各种缺陷，在描述异质零件方面更是无能为力。针对上述通用STL格式的各种局限性，目前Lipson等正在研究新的替代数据格式STL2.0。用文献[13]2.3.3节中的细化方法，得到如图2(b)所示的细化STL模型。

图2 STL模型细化

2.2 轮廓节点获取

在上述通用STL格式表示的三维模型基础上，根据零件的加工精度要求，确定STL面片细化的最小尺寸值。比较简洁的方法是直接按照通用STL格式表示的三维模型中的最小面片(如图2(a)中的最小面片尺寸为0.02 mm)为基准进行细化，从而获得STL三角面片均匀细化模型。而在STL模型中一些曲率变化较大处，针对三角面片本身就很细密的情况，为了减小运算量，在满足加工精度的前提下，可以采取多个微细三角面片合并的方式进行粗化。

通过三维软件进行三维模型的细化工作，把三维模型分解为许多细小空间三角面片，STL文件显示了各个三角面片顶点的坐标和面的法向量(指向外部)，一般相邻两个三角形有一条边重合，用许多细小空间三角面片逼近CAD零件模型，进而获得三角形均匀细化后的STL模型，如图2(b)所示。该模型中的每个三角面片的大小几乎相同，虽然数据量较通用STL格式表示的三维模型大为增加，但有利于后续的异质零件的材料特征描述。

为消除上述STL模型细化带来的数据量大及数据冗余度大的缺点，基于异质零件的功能描述需要，只需保留细化后的STL模型的节点数据(即点云数据)，并加入节点拓扑信息即可准确地描述该模型的几何信息。模型细化前后的点云数据集如图3所示。基于以上获得的外部轮廓点云数据，再按照一定的精度要求把模型进行均分，即可得到空间有序点云数据集。

图3 模型细化前后的点云数据集

2.3 基于空间微四面体的网格节点获取

基于前述已经获得的点云数据集，利用Delaunay三角剖分算法中的增量算法(也称逐点加入法)，进行各个微四面体的构造而形成新的异质零件内部表述模型，之后，再由该模型内部的各微四面体的节点按照图4所示的分解过程构造出新的网格节点数据集。该网格节点数据集与之前的点云数据集的不同之处在于：除了具有表示异质零件模型的内外曲面上的信息之外，还具有内部结构信息及内部各节点间的拓扑信息，这为进一步对异质零件模型的材料信息进行定义奠定了基础。

图4 异质零件的CAD模型网格节点获取

基于文献[13]中的微四面体建模方法，对异质零件CAD模型的材料空间描述可以使用基于微四面体的建模方法。通过建立与三维结构空间相对应的三维材料空间映射函数，即在结构特征的基础上，分别将材料特征赋予微四面体单元内的各顶点，微四面体内的微细材料分布按照该映射函数来确定，为确定异质零件CAD模型的内外表面和内部的结构信息、材料信息奠定基础。

3 基于表面轮廓的建模方法

实体内部和外部与其对应内部材料一致的结构形式是异质零件的典型结构之一，其模型应用范围也最广。对材料属性进行简化，使用外部轮廓材料直接映射零件内部材料。

异质零件的边界曲面首先按照上述方法被离散化为一系列微四面体空间单元网格。然后根据异质零件的几何特征、材料分布特征和零件功能需求，赋予网格中每个节点相应的材料信息，再根据单元网格节点的三维位置及材料值逐一计算各微四面体表面处的结构和材料分布，进而实现整个异质零件边界曲面的设计。

1)线性插值法。

异质零件微四面体内部材料信息可通过前述零件表面材料的空间线性插值得到，如图5所示。微四面体内任一点Pn的材料分布MPn为：

图5 微四面体内部材料分布

(4)

2)颜色偏置法。

轮廓平面偏置采用颜色数据不变，将几何数据偏置一段距离的方法。偏置式算法主要解决的问题是求多边形顶点偏置一段距离后的位置。截面轮廓几何数据采用偏置式算法，轮廓内部几何数据采用直线式填充。

图6 轮廓偏置方式

(5)

设A1A2的方程为：

ax+by+c=0

(6)

en的方程为：

en=ax+by

(7)

ax+by+a2×dist+b2+c=0

(8)

(9)

(10)

(11)

按照这种方法，就可以按顺序求出经过轮廓偏置后的平面顶点坐标，依次将各点连接，可形成一个完整的轮廓路径并输出完整的材料信息。

图7所示的是基于线性插值的梯度分布赋值的异质零件模型，分别为通用STL模型、均匀细化后的STL模型、均匀细化点云数据集、内部材料分布渲染图。该示例使用的是线性插值法。

图7 基于线性插值的梯度分布赋值的异质零件模型

图8所示为基于轮廓颜色偏置映射的异质零件模型，对这种曲面的内部材料进行赋值时，使用颜色偏置法更加高效。

图8 基于轮廓颜色偏置映射的异质零件模型

4 结束语

本文给出了基于微四面体网格细化的方法，通过对异质零件进行逐层分解，同时赋予网格节点材料信息，并以此为基础，构造网格表面及内部的结构和材料信息，从而完成异质零件的结构和材料的并行设计。此种基于空间微四面体的异质零件建模方法把结构设计、材料设计、模型可视化等设计过程融为一体，较其他方法具有如下优点：

1)采用了STL通用数据格式，便于与现有的CAD设计软件和3D打印设备对接，保障异质零件的CAD和CAM一体化数据格式。

2)采用网格节点定义的方式，为利用点云数据进行异质零件CAD数据的快速重构开辟了一条新途径。

后文将给出功能更强大的基于体素法的建模方法。