基于单目视觉的圆形零件直径非接触测量方法研究
尹珺瑶,朱兴龙
(扬州大学机械工程学院,江苏 扬州 225127)
单目视觉测量作为机器视觉基础技术之一,具有结构简单、信息丰富、运算快速等特点,具有广泛的应用前景。单目视觉测量通常是由CCD相机、光源、计算机和图像处理软件四部分组成。单目视觉几何相似法测量是对应于被测对象的几何参数在同一平面内的情况,根据透视投影模型,物体与其图像满足相似关系,只要从图像上提取所需参数,乘上实际放大倍数,就能得到物体的实际几何参数,是一种二维测量,主要包括几何位置、形状、变形、位移、速度测量[1],但要求此时被测面与摄像系统光轴垂直,并与像平面平行。尹英杰等[2]提出了一种基于单目视觉的平面测量方法,通过对摄像机进行简单标定,进而实现对固定平面内物体的长度测量,尽管对597 mm×597 mm地板砖的测量长度与实际长度之间的相对误差小于0.3%,但是绝对误差仍有1.3 mm,测量精度不是很高。韩延祥等[3]提出的一种单目视觉测量方法,当长度达到85 cm时,相对误差达到了11.90%,主要原因在于测试过程中不能保证摄像头的轴线垂直于被测目标平面,即使采用修正方法后,误差仍有1.48 cm,相对误差为1.68%。唐亚平等[4]针对Tsai两步标定法中初始参数不精确问题,为了提高机械零件尺寸检测精度,提出了基于直线投影约束的三步标定方法,实验结果表明,采用这种方法在尺寸检测中任意两点的距离相对误差小于0.41%。李立冬等[5]提出了一种相机针孔模型下,从单幅二维投影图像进行目标空间方位测量的方法,利用现实场景中一个三维标定块来进行相机标定,通过实验实测,在两点距离155 mm时,误差达到2 mm,在两点距离1 300 mm时,误差达到12 mm。屈珊珊等[6]提出基于单目视觉测距的测高、测面积方法,利用单目相机所建立的三维测距模型,提出了一种对任意物体实际高度进行测量的方法,其相对误差可控制在5%以内。郭宝云等[7]针对较大平面薄片类零件测量操作复杂、效率低等问题,提出基于大像幅非量测数码相机的单目视觉检测方法,实验结果表明,其测量误差小于0.1 mm。钱鹰等[8]采用射影几何自动化标定方法,完成目标物的高度测量,当标定物高度为70 cm时,相机距离标定物由近到远,测量目标高度的误差从2.150 mm增大到16.403 mm。
单目视觉测量在尺寸检测时应用较广,但存在测量精度不高的问题,主要原因是被测面与摄像系统光轴不能严格垂直并与像平面平行,因此本文针对圆形零件直径尺寸的单目视觉测量,将上述因素考虑在被测零件直径与CCD成像直径之间的解析模型之中。由于单目测量系统安装完成后,镜头焦距、镜头中心面与工作台的距离、工作台与光轴之间的夹角便固定下来,可以通过标定的方法将它们在模型中体现,因此在模型中唯一不确定因素是偏距,它随被测零件放置位置的不同,对测量精度的影响是不一样的,本文将讨论它对测量精度的影响并提出具体的解决方案。
1 圆形零件直径非接触测量的解析模型
理想状态下,镜头的光轴与相机的CCD面垂直,且光轴垂直于被测量面,图像检测的直径与零件的实际直径是一种线性关系,但是由于制造、安装等原因,当光轴与工作台不垂直时,且被测的圆形零件放置的位置不确定时,那么这种线性关系就不存在,因此有必要分析实际情况下小孔成像模型的输入输出关系。
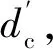
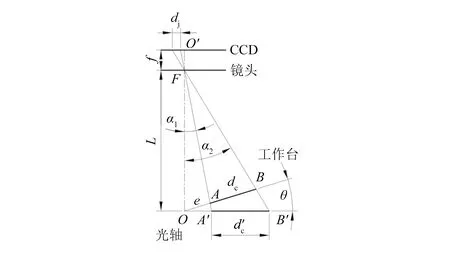
图1 实际情况下单目视觉测量解析模型
由图1几何关系可以导出:
(1)
从而可得图像直径为:
(2)
式(2)即为实际状态下的小孔成像模型,它反映了零件检测的图像直径与零件的实际直径是一种非线性关系。
由于采用小孔模型,因此L的值要适当大些,装置设计中L大于30f,这样成像近似服从透镜成像规律。f影响视场,f越大,视角越小,如果测量零件的尺寸越大,那么L就越大,测量精度就下降。θ对测量精度的影响从式(2)可以看出,当θ=0°时,偏距e对测量精度没有任何影响,式(2)变成线性关系;当θ≠0°时,这也是一般情况,此时除θ外,e的影响也会体现出来。
由式(2)可知,尽管参数L,θ,f为未知参数,但是在测量系统安装完成后,它们便是固定值,可以通过标定的方法将它们体现在模型中。然而dj还与偏距e有关,考虑到圆形零件摆放的随意性,偏距e是不确定的,如图2所示。
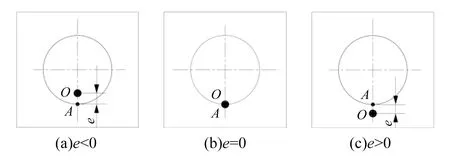
图2 视场范围内圆形零件偏距型式
图2中O点为光轴与工作台面的交点,圆表示被测圆形零件,A点为圆形零件的下边缘点。当被测零件覆盖O点,且A点在O点下方时,如图2(a)所示,定义AO之间的距离e为负偏距;当被测零件A点与O点相切时,如图2(b)所示,此时AO之间的距离e=0,定义为零偏距;当被测零件离开O点,且A点在O点上方时,如图2(c) 所示,定义AO之间的距离e为正偏距。
当L=500 mm,f=16 mm ,θ=5°,dc=20 mm时,由式(2)得到相关数据,见表1。从表1中可以看出偏距e对像直径的影响,即随着偏距的增大,像直径也越来越大。同一直径(20 mm)的零件因放置的位置不同,其像直径是不一样的,零件处于最大正偏距与最大负偏距时,两个位置的像直径之差达0.035 0 mm,像素值之差达9.37 pixel(像元大小为边长3.73 μm的正方形)。以上分析表明,被测零件的放置位置对测量精度是有影响的。
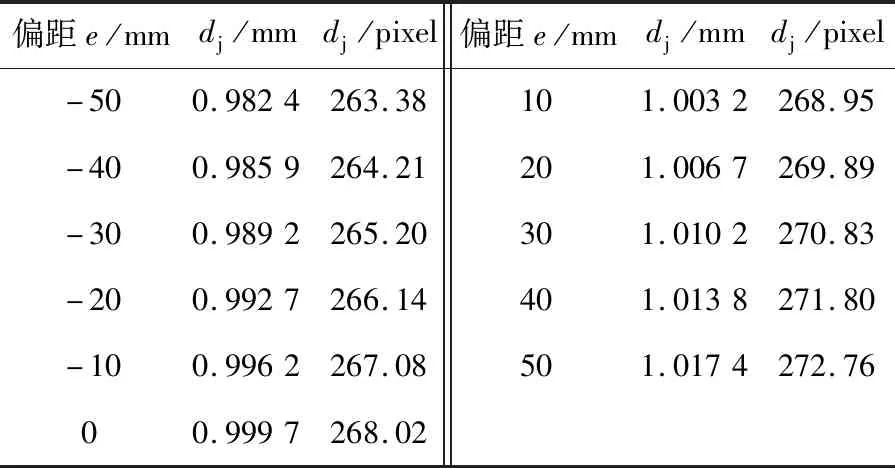
表1 偏距e对像直径的影响
如何保证e为定值,即如何保证圆形零件边缘放置时始终在测量工作台上的同一点,对提高测量精度具有重要意义。为此将工作台面设计成如图3所示的形状。台面采用有机玻璃,在测量台面上铣有台阶圆C,被测零件B放置在台阶圆内,并始终与台阶圆A点接触,这样就能保证每次测量零件的偏距是相同和固定的。

图3 圆形零件放置的位置
测量台面安装在背景光源上,尽量与相机光轴垂直,距透镜中心面500 mm。CCD采用1/3英寸,其宽度和长度分别为4.8 mm和3.6 mm,镜头焦距f=16 mm,根据视场计算,台面尺寸取100 mm×100 mm,台阶圆直径取60 mm,台阶高度取2 mm,台阶底部清根。
2 解析模型中的参数标定
2.1 单目视觉圆形零件测量系统组成
圆形零件直径测量系统由相机、镜头、上下光源、工作台、计算机等构成,如图4所示。

图4 单目视觉测量系统平台
在实验时,工作台采用有机玻璃透明材料,按图3方式加工。平台采用背光光源,将圆形零件放置在测量台面相应的位置A点处,零件将遮挡背景光,在CCD得到清晰的图像,然后通过图像处理算法即可获得圆形零件测量数据。
2.2 解析模型参数的标定
首先通过最小二乘椭圆法求得一个零件直径对应的CCD成像椭圆的短轴,一个零件直径以及它对应的CCD成像椭圆的短轴构成一个数据对。然后再对不同直径的零件进行测量,以便构成多个数据对。设不同直径dc,i(i=1,2…,n)的圆形零件,通过单目视觉得到不同的CCD图像,即不同的dj,i,由它们构成点集对(dc,dj)。根据上述点集数据,采用推导的解析模型,确定拟合函数的形式为:
(3)
式中:c1=Lfcosθ/(L-esinθ)2,c2=sinθ/(L-esinθ),且c1大于0。
在确定了拟合函数后,将式(3)转化为求无约束的优化问题,即:
(4)
式中:f(c)为最小二乘函数,其中c为(c1,c2)。
通过点集对(dc,dj),可以确定式(4)中的参数,从而获得解析模型。
根据以上提出的圆形零件直径的测量方法,通过调节光源亮度,分别放置10个不同直径(7.472~29.212 mm)的圆形零件进行测量,如图5所示。其中左图为原始图像,中间图为灰度图像,右图为轮廓图像。
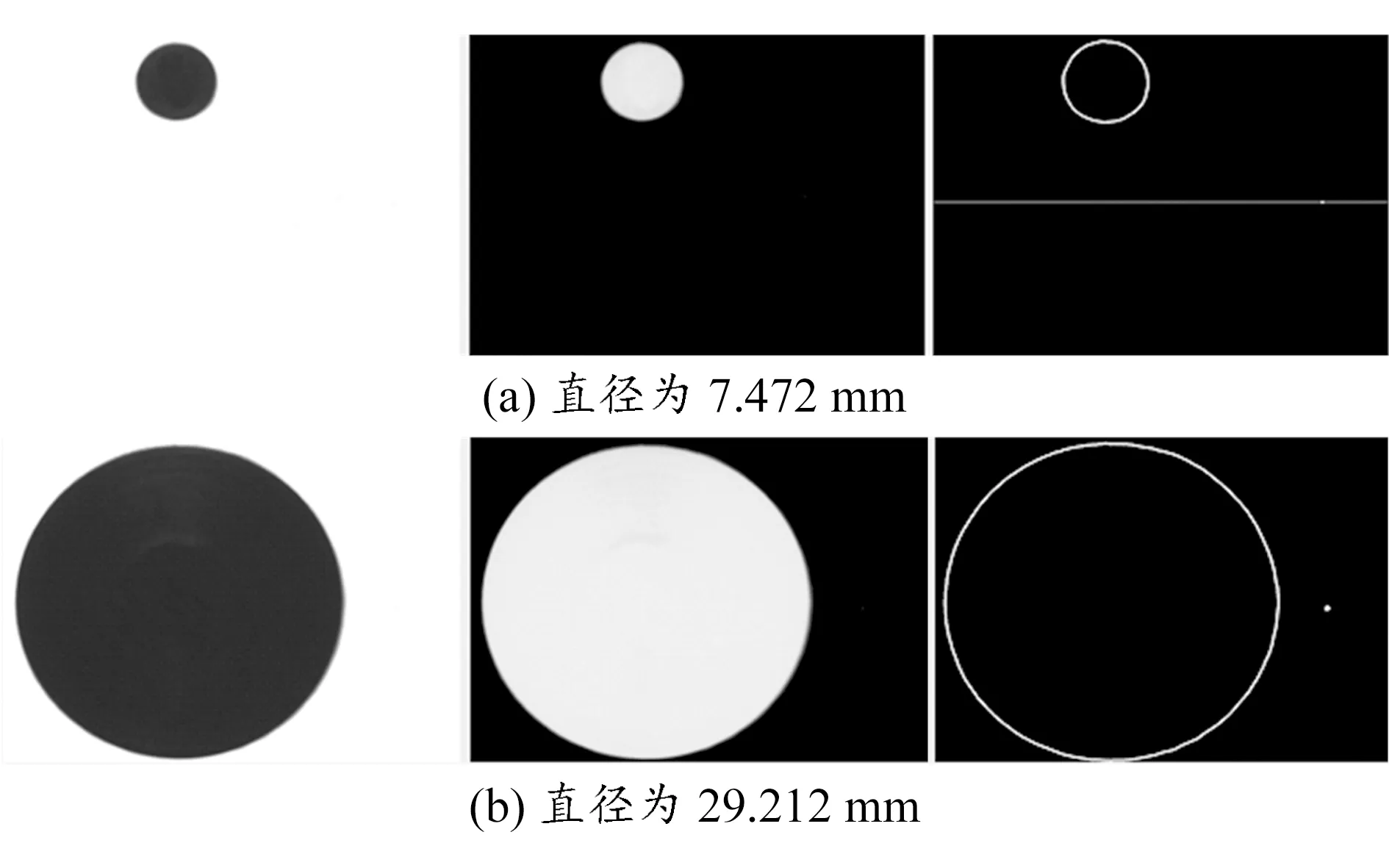
图5 实验用不同直径的圆形零件图像
根据图5中图像处理的数据,得到点集数据见表2。
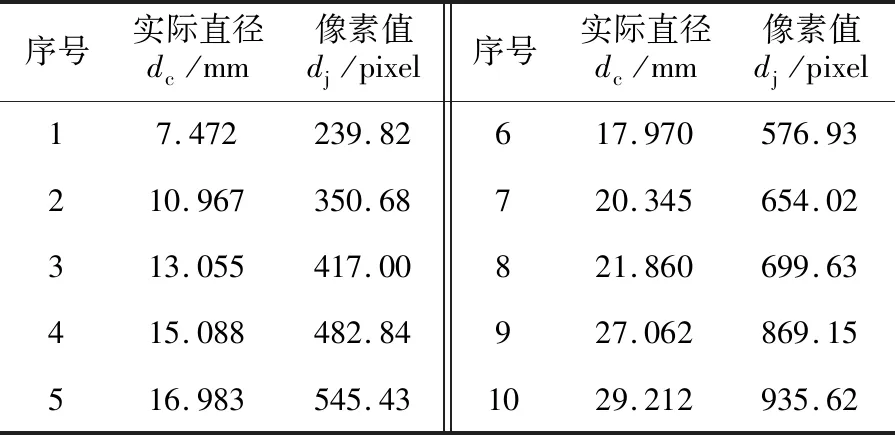
表2 点集数据
根据表2数据,采用式(4)拟合形式得到的解析模型如式(5)所示:
(5)
3 解析模型验证
为了验证该解析模型的测量精度,采用另一组9个不同直径(7.470~29.213 mm)的零件进行验证试验,获得的图像如图6所示。其中左图为原始图像,中间图为灰度图像,右图为轮廓图像。

图6 验证用不同直径的圆形零件图像
由图6获取的像直径记录在表3中,并将像直径代入式(5),获得测量的零件直径,然后与实际直径进行比较,得到误差和相对误差,结果见表3。
由表3可知,测量直径与实测直径的最大误差为0.056 mm,最大相对误差为0.187%。表3的测量直径是考虑工作台与光轴之间不垂直、且存在固定偏距e的情况下获得的。从式(5)可以看出,该解析模型是非线性模型,尽管c2非常小,这正是由于工作台与光轴之间不垂直,且存在固定偏距造成的。
若不考虑解析模型中的参数c2,则式(5)演变为线性模型,通过表3中的像直径计算得到的测量直径见表3。
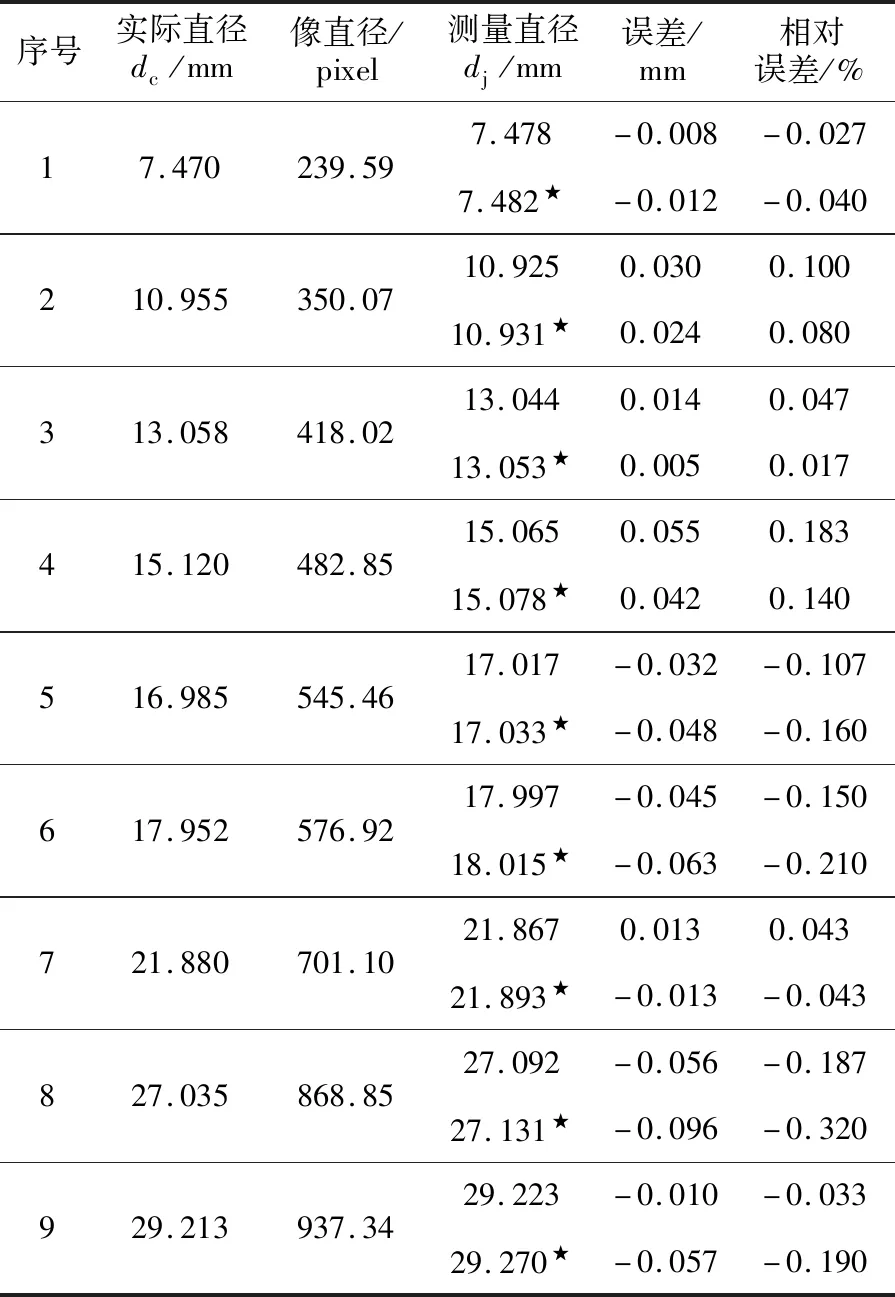
表3 测量直径与实际直径的对比
由表3可知,测量直径与实测直径的最大误差为0.096 mm,最大相对误差为0.320%,这说明在工作台与光轴不垂直、且存在固定偏距的实际情况下,若仍然按线性模型处理,测量精度会下降。从表3误差对比看,负误差绝对值变大,正误差绝对值变小,说明系统误差产生了偏移,这一偏移正是由于没有考虑工作台与光轴不垂直和存在固定偏距造成的。
4 结束语
单目测量系统安装完成后,镜头焦距、镜头中心面与工作台的距离、工作台与光轴之间的夹角便固定下来,可以通过标定的方法将它们在模型中体现,解决了被测面与摄像系统光轴不能严格垂直,不能保证摄像头的轴线垂直于被测目标平面等问题,提高了测量精度。针对解析模型中唯一不确定因素——偏距,讨论了偏距参数对解析模型测量精度的影响,并提出了消除影响的具体解决方案。采用不同直径的零件对解析模型进行了验证,并与线性模型进行了对比,结果表明采用非线性解析模型的测量精度优于线性解析模型。

