比较法在信号与系统课程教学中的应用

张静 陶彬彬

摘要：信号与系统这门课程抽象、理论性强、基本概念、数学公式及推导较多，学生不容易理解，容易望而生畏，学习起来倍加困难，但是好的方法可以使信号的学习效果达到事半功倍。比较法是一种特别适合于信号与系统课程的教学方法，将比较法用于实际的教学，不仅可以激发学生的学习热情，提升学习效果，而且可以提高学生的学习能力。

关键词：连续系统;离散系统;卷积;傅里叶变换;拉普拉斯变换

中图分类号：G642.4      文献标识码：A

文章编号：1009-3044（2021）26-0261-03

开放科学（资源服务）标识码（OSID）：

1 背景

信号与系统课程是电子信息类专业的一门重要的专业基础课，该课程是一门承上启下的课程，其先修课程为高等数学、电路原理、复变函数等，其后续课程有自动控制原理、高频电子线路、通信原理、数字信号处理等[1-2]。该课程理论性较强，数学公式颇多、基本概念、基本分析方法很重要，并且因为数学颇多、理论性强、比较抽象，所以学好信号这门课程需要花费很多的精力。因此，好的学习法对于信号与系统课程的学习，不仅可以事半功倍，而且可以激发学生的学习热情，进而提升信号的学习效果，为后续课程的学习以及考研打下牢固良好的基础。

信号与系统课程主要包括：连续系统的时域分析、离散系统的时域分析、傅里叶变换和系统的频域分析、连续系统的s域分析、离散系统的z域分析、系统函数及状态变量等[3]。本文以信号与系统前6章的内容为例，将比较法用于其中。通过比较法不仅将连续系统与离散系统时域内的基本信号与性质、卷积、响应的求解进行比较，而且将三大变换域-频域、复频域、z域进行比较。通过比较法发现相似规律及差异，进而可以更好地掌握信号系统的基本理论，构建系统性的知识体系。

2 连续系统与离散系统的基本信号及性质的比较

连续系统及离散系统中有一些基本的信号，基本信号有其独特的性质以及响应，他们有很多相似的地方，可以对比掌握。基本信号的波形图如图1～图4所示。基本信号、响应、关系及性质如表1所示。

2 卷积积分和卷积和的比较

2.1 定义式

卷积积分：

[ft=f1t*f2t=-∞+∞f1τ?f2t-τdτ]             （1）

卷积和：

[fk=f1k*f2k=-∞+∞f1i?f2k-i]               （2）

无论卷积积分还是卷积和都分为5步走，即：换元、反转、右移、相乘、积分（求和），唯一不同的是连续信号的积分对应离散信号的求和。

2.2 卷积积分和卷积和的性质

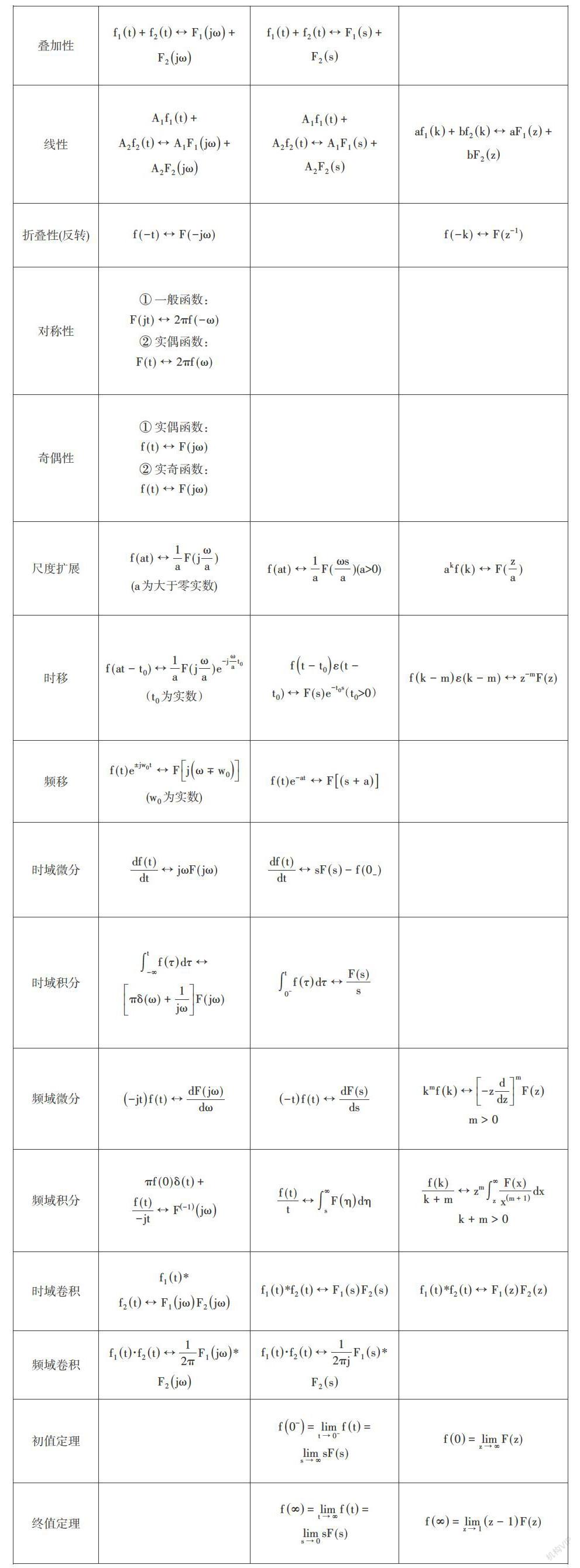
卷积积分和卷积和有很多重要的性质，灵活的运用性质可以简化卷积的运算[4]。表2为卷积积分和卷积和的性质，他们有着相似之处，运用比较法可以帮助理解、记忆、掌握。

从表2可以发现卷积积分和卷积和的性质类似，区别在于前者为连续变量，后者为离散变量。连续信号里面求原函数的积分对应离散信号求迭分，連续系统的微分对应于离散系统的差分。

2.3 卷积的求解方法

卷积积分的求解方法有：1）定义式法;2）图解法：3）性质法。

卷积和的求解方法有：1）定义式法;2）图解法：3）性质法 ;4）不进位乘法求卷积和;5）列表法。

2.4 卷积法求零状态响应

连续系统，对于任意[ft]通过LTI系统产生的零状态响应等于其卷积该系统的冲击响应，即：[yzst=ft*ht];

离散系统，对于任意[fk]通过LTI系统产生的零状态响应等于其卷积该系统的单位序列响应，即：[yzsk=fk*hk];

只要知道系统的冲击响应[ht]或者单位序列响应[hk]，对于任意信号[ft]或[fk]，就可以求出他们的零状态响应[yzst]或[yzsk]。

3 连续系统与离散系统求解响应的比较

连续系统的全响应：

[yt=yht+ypt=yxt+yft]，连续系统全响应分为自由响应[yht]和强迫响应[ypt]，也可以分为零输入响应[yxt]和零状态响应[yft]。

离散系统的全响应：

[yk=yhk+ypk=yxk+yfk]，离散系统全响应分为自由响应[yhk]和强迫响应[ypk]，也可以分为零输入响应[yxk]和零状态响应[yfk]。

无论是求解连续系统的微分方程还是求解离散系统的差分方程相同的是都包含以下几个步骤：1）特征方程的求解 ;2）求初始值 ;3）求齐次解; 4）求特解 ;5）通过初始值求待定系数等。也就是说求解思路是一样的。所不同的是，求初始值的方法不同，前者初始值用积分求，后者的初始值用递推;齐次解的表达式也不一样，前者，特征根在指数上，后者特征根在底部。

4 傅里叶变换与拉普拉斯变换、z变换的比较

4.1 三者之间的关系[3]

[ft]的傅里叶变换为[Fjω]，简记作[ft?Fjω]，[Fft=Fjω]，

[Fjω=-∞+∞fte-jωtdt]，                               （3）

傅里叶逆变换为：

[F-1Fjω=ft=-∞+∞Fjωejωtdω]                     （4）