如何有效提高初中生数学计算准确率的策略

张艳霞

【摘要】数学学科的本质和基础是计算，所以初中数学教师要想提高学生的数学成绩，就要提高学生数学计算的准确率.本文首先分析数学计算的意义，其次从四个主要的方面阐述有效提高初中生数学计算准确率的策略，最后做出总结.

【关键词】初中数学;计算准确率;实际意義;具体举措

计算是数学学科的基础.初中生要想学好数学，取得好的成绩，就必然要提高计算的准确率.初中生在学习数学的过程中，计算的准确率不但是影响他们取得优异数学成绩的重要因素，也是影响他们数学学习信心的主要因素.所以，提高初中生数学计算准确率是数学教师的教学重点.本文将就如何提高初中生数学计算准确率的具体举措展开讨论，详细内容如下.

一、提高数学计算准确率的意义

第一，计算是学习数学的基础，只有掌握了计算的方法和技巧才能够学好数学.当前影响初中生数学学习兴趣和信心的主要因素是他们经常在计算的过程中出现错误，进而难以取得优异的数学成绩，久而久之就会极大挫伤学生学习数学的积极性和主动性.

第二，数学计算将会伴随着每个人一生，学好和用好数学计算不仅对提高学习成绩有积极意义，也会为每个人未来的工作和生活提供帮助.有效提高初中生数学计算的准确率将有利于他们打好数学基础，为高中以及更深层次的数学学习贡献力量.

二、有效提高初中生数学计算准确率的策略

（一）培养良好的计算习惯

良好的计算习惯不仅包括仔细审题、不漏写、不错写等，还包括计算的过程要集中注意力，不能走神和分心等.只有养成良好的计算习惯，初中生才能够显著提升计算的准确率.初中生要想养成良好的计算习惯，应当从以下几个方面来进行培养.

1.端正态度，认真对待

首先，初中数学教师无论是在课上还是在课下，都要向学生反复强调细心、耐心、认真的重要性.初中生在做计算题的时候一定要保证态度端正，不要从心理上轻视每一个计算步骤，而要养成注重计算过程中每一个步骤的习惯，尽管有些题不会有太多的计算步骤就能够得出答案，但是初中生也要给予足够的重视，按照既定的运算步骤一步一步地求解.

例如，初中数学教师在讲授“解不等式”的计算题时，从教学的开始阶段就要让学生注意计算过程中出现的每一个数字以及题干中要求使用的加减乘除运算方法，且在按部就班求解的过程中要看清数字，准确写出运算符号，观察是否有同类项，灵活运用所学知识尽量优化计算的步骤，降低计算过程中出现错误的概率，从而提高计算的准确率，避免出现低级错误（如图1）.

2.字迹工整，规范计算

初中数学教师无论是在课上还是在课下，一定要向学生反复强调，在解题过程中每一个解题步骤都要保持字迹工整、清晰明了，不要胡写乱画，或者嫌麻烦而缩写和简写，这对于提高初中生数学计算准确率有着非常重要的帮助.因为如果学生在解题计算的过程中追求速度而省略了一些关键步骤，而这些中间环节有可能就是影响学生得出最终准确答案的直接因素，所以初中生应当在计算的过程中将每一个运算步骤都清晰地记录下来，这不但能够提高准确率，还能够在后期检查的过程中有内容可依照，一旦中间的解题步骤出现了符号或运算方向的错误，就能够立即发现并纠正，这也能够帮助学生省略再次演算和再次检查的时间.初中数学教师在教学的过程中要让学生养成字迹工整的习惯，这将会在很大程度上提高学生的计算准确率.

（二）熟记数学公式和法则

初中数学教师要让学生牢记数学运算法则和基本公式.根据数学教师的教学经验显示，大多数初中生无法提高数学计算准确率的原因是他们并不熟悉教材内的公式、定理和运算法则，这就让学生在做计算题的时候不能够快速地从大脑中调取解决每一道题所需要的知识，也就容易让学生进展到某一个计算步骤时陷入停滞状态，所以初中数学教师在教学过程中要反复强调熟悉运算法则和基本公式的重要性.

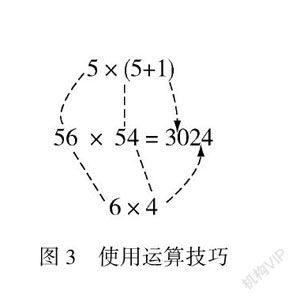
第一步是让学生牢记教材中的运算法则和基本公式，第二步则要通过反复练习来提高他们运用公式和法则的熟练度，第三步是让学生做一些较为复杂的计算题，提高他们对于运算法则和基本公式的运用程度.例如，初中数学教师在教授学生有关求解各个角的度数的相关知识时，要先让学生熟悉四边形、三角形等常见图形的一些基础定理，如“三角形的内角和是180°”“四边形的内角和是360°”“直角三角形中30°角对应的边，长度是斜边长度的一半，反过来也可以计算各个角的度数”等.当学生在计算有关多边形求角度数以及多边形角与边的关系的题时，就要能够快速调取如上所述的知识点，这对于学生快速梳理解题思路、找到解决问题的关键点有重要的帮助.

总而言之，初中数学教师在教学过程中要想提高学生数学计算的准确率，就要让学生对教材中的运算法则和基本公式了然于心，先进行背诵，然后通过做题进行理解和强化记忆，最终让初中生在解题的过程中快速搜集所学知识，并学会灵活运用.

（三）提升检查意识

初中数学教师要想提高学生数学计算的准确率，也可让学生养成检查的习惯.当学生完成了某一道或几道数学计算题的解题后，应让他们进行检查，这是提高计算准确率的重要举措.学生在检查的过程中可以依靠第一次记录的解题步骤来判断自己的解题思路是否出现偏差，判断自己在第一次解题过程中的每一个步骤是否出现了看错数或者写错数等情形，一旦学生在检查的过程中发现了第一次解题过程中的步骤有不规范或者不正确的情况，那么就可以及时纠正，进而按照正确的解题步骤进行计算，提高准确率.

例如，学生在列方程解答应用题时，中间涉及的运算步骤比较多，一旦某一个环节出现差错就会造成最终结果的错误，因此，学生在运算结束后应重新对整个解题的过程进行检查，判断公式是否运用得当、符号是否正确等，一旦发现出现错误就要及时纠正（如图2），保证整个运算的各步骤之间都是完整且无误的，最终提高计算的准确率.