RC桥墩残余位移指标影响因素分析及贝叶斯估计

曾武华， 卓卫东， 王东升

(1. 三明学院 建筑工程学院， 福建 三明 365004； 2. 福州大学 土木工程学院， 福州 350108；3. 河北工业大学 土木与交通学院， 天津 300401)

传统的桥梁抗震设计方法通过提供结构足够的强度和延性，防止其在大震作用下发生倒塌破坏[1]。然而，由于抗侧力的关键构件(如桥墩等)在大震中受损严重或整体残余位移过大等原因，桥梁往往在震后需要拆除重建。1995年日本阪神地震震害调查发现，若钢筋混凝土(reinforced concrete，RC)桥墩的残余位移比(即墩顶残余位移与墩高之比)超过1.75%，桥梁就需要拆除重建[2]。由此可见，钢筋混凝土桥墩的残余位移比可作为桥梁结构抗震韧性设计的重要参数之一。目前，桥墩残余位移验算已被写入一些国家的桥梁抗震设计规范，被认为是桥梁结构可修复性的重要描述指标[3-5]，但我国现行桥梁抗震设计规范[6]尚缺乏关于残余位移的相关规定。

已有研究认为，强震后钢筋混凝土桥墩的可修复性可通过定义无量纲化的残余位移指标来量化评价。Hose等[7]在对大量钢筋混凝土墩柱拟静力试验结果分析的基础上，定义了一个以屈服位移为归一化参数的无量纲化的残余位移指标——残余位移延性指标。罗征等[8]基于5根钢筋混凝土空心墩柱的拟静力试验结果，探讨剪跨比和配箍率对残余位移延性指标的影响，发现剪跨比与配箍率两参数的变化对残余位移延性指标无影响。王军文等[9-10]采用数值模型，计算分析了轴压比、长细比、纵筋配筋率、体积配箍率、纵筋强度硬化系数、纵筋与混凝土强度比等参数对桥墩残余位移延性指标的影响；结果表明，钢筋混凝土桥墩残余位移延性指标随轴压比、纵筋强度硬化系数、体积配箍率、长细比的增大而减小。此外，还有一些研究分别提出了以墩高、最大位移等作为归一化参数的无量纲化的残余位移指标定义。李宇等[11]采用桥墩残余位移比，定量化描述了桥梁结构5个不同水平的损伤性能目标。蔡晓玉等[12]以一座连续梁桥为研究对象，采用增量动力分析方法，得到了基于桥墩残余位移比的结构倒塌判定指标。曾武华等[13]基于钢筋混凝土桥墩的拟静力试验结果，给出极限状态下桥墩残余位移比的统计结果。胡晓斌等[14]研究了强震作用下单自由度体系残余位移的离散性问题，结果表明，残余位移及残余位移延性指标的离散性最大，而残余位移与最大位移之比的离散性最小。

由于影响钢筋混凝土桥墩残余位移指标的因素较多，目前学者们对残余位移指标的影响因素及其影响程度仍未达成共识；此外，已有试验和分析数据等均具有一定的不确定性，目前发现其残余位移的统计离散性较大。鉴于此，本文结合拟静力试验和数值模拟分析，研究钢筋混凝土桥墩的基本设计参数对其残余位移指标的影响规律，并采用回归分析方法得到其残余位移指标的经验计算公式；在此基础上，基于贝叶斯更新理论对残余位移指标进行估计，建立钢筋混凝土桥墩残余位移指标的概率模型。

1 残余位移指标影响因素分析

1.1 有限元计算模型

为了验证数值模型的可靠性，利用OpenSees软件，首先建立Lehman等[15]试验采用的钢筋混凝土墩柱试件的有限元计算模型；其中，墩柱试件采用基于力的非线性梁柱单元模拟；混凝土本构关系采用concrete04模型，约束混凝土的本构采用的是Mander提出的约束混凝土应力-应变关系，钢筋本构关系采用reinforcingsteel模型[16-18]。对计算模型施加试验反复荷载，模拟Lehman等开展的拟静力试验。

图1和图2分别给出了Lehman等试验中两个典型试件(415试件和430试件)的试验滞回曲线与数值滞回曲线的对比情况；从图1中可见，两者吻合较好。

图1 415试件试验结果与数值计算结果比较

图2 430试件试验结果与数值计算结果比较

1.2 参数分析

已有研究表明，钢筋混凝土桥墩的轴压比、剪跨比、配筋率和配箍率是影响其震后残余位移的主要因素。由于受到经费、时间等条件限制，已有试验无法全面考虑这些因素对钢筋混凝土桥墩残余位移的影响，故本文以轴压比、剪跨比、配筋率和配箍率作为基本参数，每个参数取4个水平(如表1所列)，采用全面试验设计方法，通过改变Lehman等试验试件的相应参数，建立了256个圆形桥墩试件样本。

利用OpenSees软件，采用1.1节经验证的建模方法，建立所有桥墩样本的有限元计算模型，进行拟静力加载。通过有限元计算分析，得到了256个圆形桥墩试件的荷载-位移滞回曲线，以及桥墩试件在变形极限状态下的残余位移及最大位移值。本文将以下3个条件： ① 纵向钢筋屈曲；② 水平箍筋断裂；③ 桥墩水平承载力下降到最大承载力的85%；之一发生即定义为桥墩变形极限状态达到的标志。为了确定桥墩残余位移能力，仅考虑桥墩达到变形极限状态时，其卸载后的墩顶残余位移。

本文分别以墩高和最大位移作为归一化参数，定义两个无量纲化的残余位移指标，即残余位移比δrh和残余位移与最大位移比δrm，分别如式(1)和式(2)所示

δrh=Δr/H

(1)

δrm=Δr/Δm

(2)

式中：Δr为当桥墩达到变形极限状态时，其卸载后墩顶残余位移；H为墩高；Δm为当桥墩达到变形极限状态时，墩顶最大位移。

根据式(1)和式(2)的定义，采用统计分析方法，得到了256个桥墩试件的残余位移指标δrh和δrm的统计特征值，如表2所示。由表2可见，残余位移比δrh的变异系数大于残余位移与最大位移比δrm的变异系数，说明残余位移与最大位移相关性更强。

表2 钢筋混凝土桥墩残余位移指标统计特征值。

将256个桥墩试件残余位移与最大位移比δrm的计算结果绘制成直方图及高斯分布拟合图，如图3所示。图3表明，残余位移与最大位移比δrm统计直方图与高斯分布拟合较好。

图3 残余位移与最大位移比直方图及高斯分布拟合曲线

1.3 残余位移指标均值影响参数

为了研究基本参数对钢筋混凝土桥墩残余位移指标的影响规律，分别将轴压比、剪跨比、纵筋率或箍筋率取为表1中的某一水平，统计其他参数变化情况下残余位移指标δrh和δrm的均值。例如，在轴压比水平为0.1时，对应桥墩试件为64个，通过对64个桥墩试件的残余位移指标δrh和δrm的统计分析，可得到其平均值；同理，可得其他给定参数水平下各残余位移指标δrh和δrm的平均值。表3列出了各基本参数取不同水平时残余位移指标δrh和δrm的平均值；由表3可见，残余位移指标δrh和δrm的平均值随着轴压比、剪跨比等设计参数变化趋势相同，残余位移比δrh的平均值在1.46%～5.32%变化，而残余位移与最大位移比δrm的平均值在0.52～0.75变化。

表3 残余位移指标均值

图4～图7显示了轴压比、剪跨比、纵筋率和箍筋率对残余位移指标δrm均值的影响。由图4和图5可知，δrm随轴压比增大而减小，且随剪跨比增大而增大；但当剪跨比大于6时，剪跨比对残余位移指标δrm的影响趋缓。由图6和图7可知，δrm随纵筋率和箍筋率增大而增大，但变化幅度均较小。采用线性回归分析方法，应用Origin软件拟合出残余位移指标δrm与轴压比等4个影响因素的关系。

图4 轴压比对残余位移与最大位移比均值的影响

图5 剪跨比对残余位移与最大位移比均值的影响

图6 纵筋率对残余位移与最大位移比均值的影响

图7 箍筋率对残余位移与最大位移比均值的影响

表2表明，残余位移指标δrh和δrm的统计特征值中变异系数分别为0.53和0.19，存在较大的离散性。因此，需要综合考虑各影响因素，提高残余位移指标能力预测的有效性。综合考虑轴压比等4个主要影响参数，基于256个桥墩试件样本模拟结果，应用Origin软件进行多元回归分析，得到残余位移指标δrh和δrm的概率分布模型。分别式(3)和式(4)所示

(3)

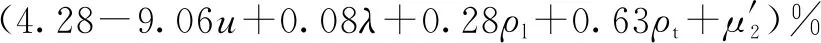
(4)

2 贝叶斯概率参数估计

2.1 贝叶斯更新理论

采用贝叶斯更新理论，可综合考虑经验计算公式和观测数据存在的固有不确定性与认知不确定性，获得桥墩残余位移指标后验分布概率模型。根据贝叶斯理论，若随机变量Θ先验分布概率密度函数为f′(θ)，通过获取拟静力试验观测数据，参数先验分布进行更新得到后验分布可为

f″(θ)=kL(θ)f′(θ)

(5)

拟静力试验结果ε为一组观测值(x1,x2,…，xn)，该组值代表了概率密度函数为fX(x)的总体X的一个随机样本。似然函数L(θ)为X在(x1,x2,…，xn)处概率密度函数之积，即

(6)

假定参数服从正态分布，由式(6)可知，参数μ的似然函数为L(μ)，可表示为

(7)

因此，参数μ的后验分布变为

(8)

式中：μ′为先验分布均值；σ′为先验分布标准差。

由共轭分布可知[19]，先验分布为正态分布，后验分布也为正态分布，其更新后均值μ″和方差σ″表示为

(9)

(10)

2.2 试验观测值

Lehman等完成的815、1015和407模型桥墩截面尺寸为609.6 mm，混凝土强度为31 MPa，主筋屈服强度为462 MPa，表4列出了轴压比等4个主要参数取值。表5为Lehman等完成的3个试件观测结果。

表4 RC桥墩拟静力试验试件参数值

表5 RC桥墩拟静力试验观测值

2.3 后验分布

残余位移指标先验概率分布用式(3)和式(4)表示。基于表5所列3个桥墩拟静力试验观测结果，采用贝叶斯更新理论推导的式(9)和式(10)，可建立残余位移指标后验概率分布，表示为

δrm=0.62-0.54u+0.02λ+0.03ρl+

(11)

(12)

通过对比残余位移指标先验概率分布与采用贝叶斯更新后残余位移指标后验概率分布，结果表明，残余位移与最大位移比δrm标准差由0.10减小到0.04，残余位移比δrh标准差由1.48减小到1.13，残余位移指标离散性有所下降。

3 贝叶斯估计应用

为了验证贝叶斯更新后的残余位移指标概率分布模型估计的有效性，本文选取了5个墩柱构件拟静力试验结果进行验证，表6和表7所述试件来源5个试验数据均来源于美国太平洋地震工程研究中心的结构特性数据库[20]。表6列出了所有试件基本参数值。采用残余位移指标先验分布和后验分布可对5个拟静力试验构件结果进行验证，结果如表7所示。

表6 RC桥墩拟静力试验试件参数值

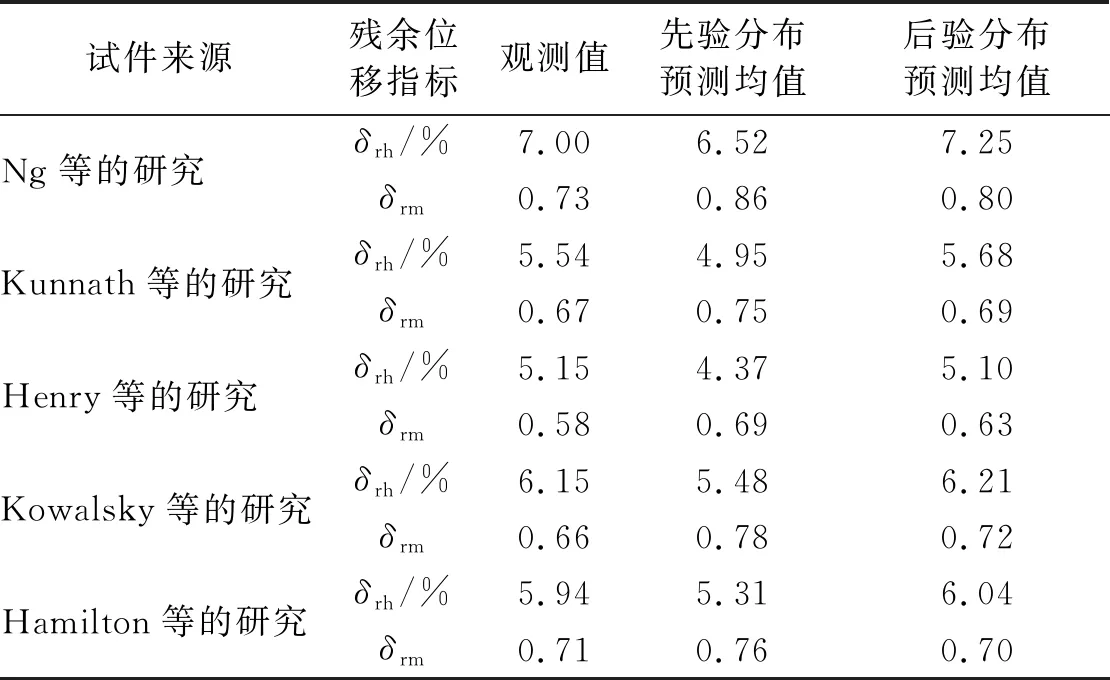
表7 RC桥墩残余位移指标贝叶斯估计

总体上来看，由表7可得，所有试验构件的残余位移指标试验结果采用更新后的后验分布预测准确性要优于先验分布预测的结果；采用后验分布对残余位移指标预测结果与试验结果误差率能够控制在10%以下，在工程可接受范围之内。

4 结 论

(1) 在轴压比、剪跨比、纵筋率和箍筋率4个影响因素中，轴压比对钢筋混凝土桥墩残余位移指标影响最大，且残余位移指标均值随轴压比的增大而减小。

(2) 钢筋混凝土桥墩残余位移指标均值随剪跨比、纵筋率和箍筋率的增大而增大，但总体增加幅度不大。

(3) 建立了拟静力作用下桥墩残余位移指标概率模型，可用于抗震性能设计和评估时残余位移指标估计。

(4) 基于贝叶斯更新理论，综合利用先验信息和拟静力试验观测信息更新获得后验分布估计，计算更具科学性，能够在试验数据样本不大的条件下估计参数的概率特性。