高精度组合剩余静校正方法及其应用

徐兴荣，苏 勤，孙甲庆，曾华会，肖明图，刘梦丽

（中国石油勘探开发研究院西北分院，兰州 730020）

0 引言

根据保真处理需求，解决好基础静校正以后，通常需要剩余静校正进一步消除中短波长静校正量的影响［1-3］。目前常用的方法主要有3 类：一是基于相关算法的地表一致性剩余静校正方法，通过相关拾取地震道时移量进行反演，分解得到炮、检点剩余静校正量，此类方法计算效率相对较高，但当地下构造复杂或资料信噪比偏低时，不能很好地满足地表一致性假设条件，此时可能产生“周期跳跃”，此类方法便会失效［4-6］。二是基于非地表一致性假设的剩余时差校正方法，常用的是TRIM 剩余静校正，但此类方法若不能很好的控制剩余静校正参数，很容易产生假构造，特别是针对新勘探区块，处理工程师对地下构造认知度不高时，一般是慎用的［7-9］。三是基于全局寻优算法的剩余静校正方法，此类方法理论上可以解决大周期的剩余静校正问题，但在低信噪比、复杂地下构造区应用时，局部收敛过慢，全局搜索能力会得到抑制，其计算结果很难预知，对处理人员综合素质要求较高，并且其计算效率较低，因此针对大数据量三维工区，此类方法也很少被采用［10-12］。

为了克服上述传统剩余静校正方法各自的局限性，提出了一套高精度的组合剩余静校正方法。首先，基于地表一致性剩余静校正理论，采用空变多时窗融合剩余静校正方法，建立空变的模型道，提高剩余静校正对模型道信噪比要求，再采用多尺度分频剩余静校正方法消除频率对模型道的影响，最后，在成像道集上，基于共成像点（CIP）道集的时变剩余静校正方法，消除残留剩余静校正问题，以期能够彻底地消除中短波长静校正量的影响，达到提高成像精度的目的。

1 高精度组合剩余静校正方法

空变多时窗融合剩余静校正方法和多尺度分频剩余静校正方法具有地表一致性剩余静校正的高效优势，而且比传统地表一致性剩余静校正的精度更高，基于共成像点（CIP）道集的时变剩余静校正方法可以进一步消除残余剩余静校正量。

1.1 空变多时窗融合剩余静校正

限制地表一致性剩余静校正方法在低信噪比、复杂构造区应用的主要原因是无法在这些区域获取精确的动校正速度，无法形成准确的模型道。动校正速度不准确，会导致动校正后的资料存在较大的剩余时差［13-15］，速度误差造成的剩余时差为

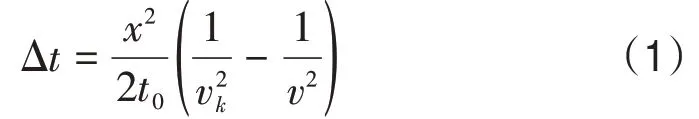
式中：t0自激自收时间，s；x为炮检距，m；v为准确的动校正速度，m/s；vk为实际采用的动校正速度，m/s。

不同层位的剩余时差不同，在地震资料中表现出类似非地表一致性的静校正问题，使用这种资料进行剩余静校正量的计算时，无法保证叠加后各个层位都得到改善。图1 是剩余时差与速度误差的关系曲线，为了测试剩余时差与速度误差之间的关系，在t0=1.2 s，x=1 200 m 处设置速度v=2 200 m/s的一套反射地层，当速度误差为15%时，剩余时差约为50 ms，因为剩余时差会随着速度误差的增大而急剧增加，当速度误差为50%时，其剩余时差约为380 ms。

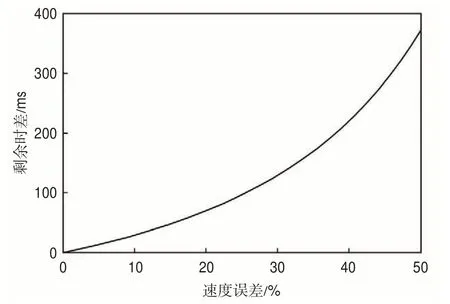
图1 剩余时差与速度误差关系Fig.1 Relationship between residual time difference and velocity error

为了避免“双复杂”（近地表复杂、地下构造复杂）及低信噪比区因动校正速度不准确而引起剩余静校正畸变，通常需要选取信噪比较高、同相轴连续性较强的构造区域建立模型道。在实际资料处理及剩余静校正量的计算过程中，通常只能在全区采用一个固定时窗进行计算。在地下构造空间变化比较剧烈时，却很难保证在一个时窗内计算出高标准的模型道［16-17］。

图2 是北非乍得Daniela 东区块的现场三维偏移剖面。该工区地下构造空间变化较快，由于剩余静校正量无法实现三维拼接，通常会选用单一计算时窗，采用地表一致性剩余静校正方法计算其剩余静校正量。实际处理过程中，通过优化，分别选取并试验了W1时窗（700～2 100 ms），W2时窗（200～1 000 ms），W3时窗（200～1 500 ms），计算出3 套剩余静校正量。通过成像效果对比发现，3 个单时窗均无法获取适应于全区高精度成像的剩余静校正量，但在三维空间内，3 个不同的时窗都有区域性的剩余静校正效果，如图2（b）所示，采用W1时窗计算的剩余静校正量，在绿色区域内获得了较好的剩余静校正效果；采用W2时窗计算的剩余静校正量，在蓝色区域内获得了较好的剩余静校正效果；采用W3时窗计算的剩余静校正量，在红色区域内获得了较好的剩余静校正效果。因为三维地震资料无法实现剩余静校正量的拼接，本文提出了一种空变多时窗融合剩余静校正方法，其最终目的就是在各自适应区内，保留成像效果最好的计算时窗所计算的剩余静校正量。

图2 乍得Danila 东区块现场偏移剖面（a）及工区分布图（b）Fig.2 Field migration section（a）and work area distribution（b）of Danila East Block in Chad

空变多时窗融合剩余静校正方法的理论仍基于地表一致性假设，只是技巧性地采用空变时窗，按照地下地质构造的空间展布特征，选取信噪比更高的模型道，分别拾取时移量，然后按空间适应范围，统一分解到炮、检及共中心点。

其具体实现步骤如下：

①根据地下构造的空间变化趋势，确定模型道窗口的时间范围及窗口个数。以图2 所示乍得资料为例，采用3 个计算时窗：W1，W2，W3，采用传统的互相关剩余静校正思路，分别计算其模型道Mod1，Mod2，Mod3，然后分别拾取各自分解剩余静校正量，获得对应时窗的3 套剩余静校正量M1，M2，M3。

②分别加载之前计算的多套剩余静校正量M1，M2，M3，进行叠加成像效果对比，并找出分别加载剩余静校正量后获取较好成像质量的空间区域S1，S2，S3［图3（a）］。

③实现不同窗口计算模型道的空间融合。在S1区域内采用W1时窗所计算的模型道Mod1，在S2区域内采用W2时窗所计算的模型道Mod2，在S3区域内采用W3时窗所计算的模型道Mod3，在空间上实现模型道的融合，形成新的融合模型道Mod。

④统一采用高斯-赛德尔迭代进行分解，获得一套剩余静校正量，通过空变多时窗融合获取的剩余静校正量M。在S1区域内采用W1时窗计算的剩余静校正量M1，在S2区域内采用W2时窗计算的剩余静校正量M2，在S3区域内采用W3时窗计算的剩余静校正量M3。由于是统一分解，在三维空间内的拼接位置不会出现静校正量拼接时差［图3（b）］。

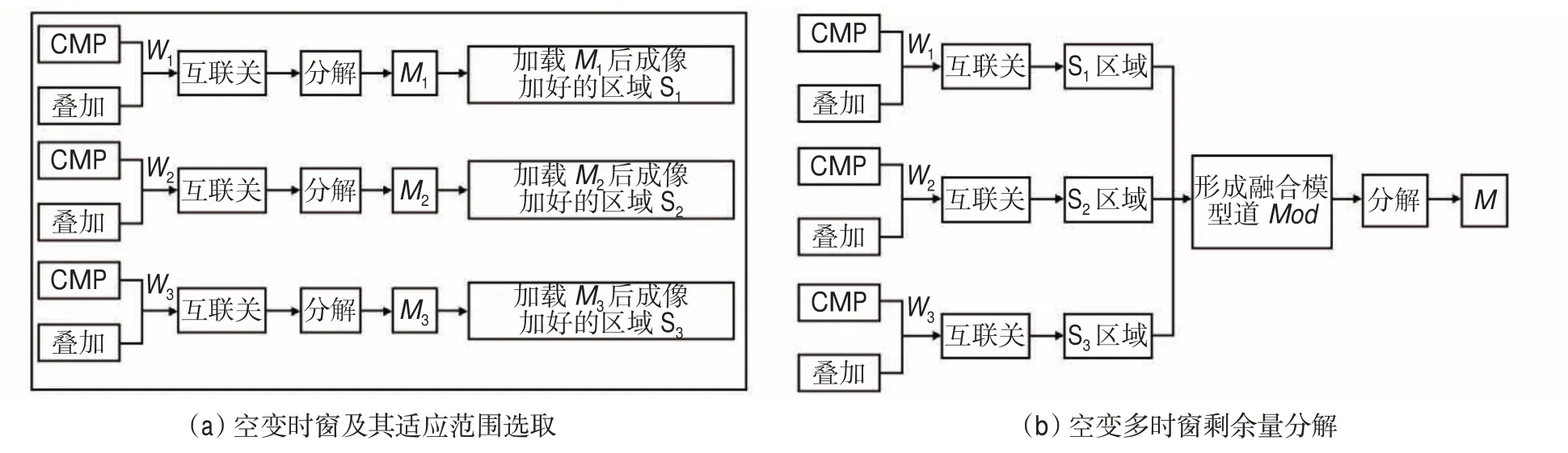
图3 空变多时窗融合剩余静校正量计算Fig.3 Calculation of residual static correction of space variant multi-time window fusion

针对实际资料，可以根据资料地下构造的空间变化趋势，分多个空间范围、多个时窗进行剩余静校正量的空间融合。

1.2 多尺度分频剩余静校正

计算剩余静校正量模型时，通常采用有效频带全部地震记录进行模型道的估算，忽略了频率对于模型道产生的误差，而随着宽方位、宽频、高密度（“两宽一高”）地震采集越来越多，保真成像要求越来越高，需进一步研究频率对剩余静校正量的影响［18-20］。为确定高精度模型道的有效频率范围，阐明多尺度分频剩余静校正方法开展的必要性及基本原理，先计算频率对剩余静校正模型道的影响

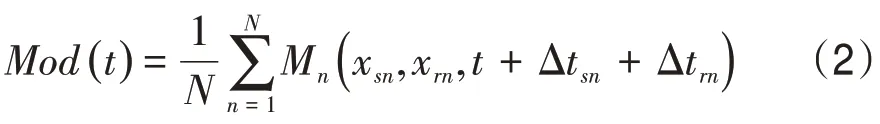
式中：Mod(t) 为不存在静校正量的地震记录；M是各炮点及接收点的静校正量构成的向量；N为CMP响道集内的地震道数；Δtsn为炮点静校正量，s；Δtrn为接收点静校正量，s；xsn为道集第n个地震道的炮点静校正量，s；xrn为道集第n个地震道的检波点静校正量，s。

通过傅里叶变换，将式（2）转换至时间域

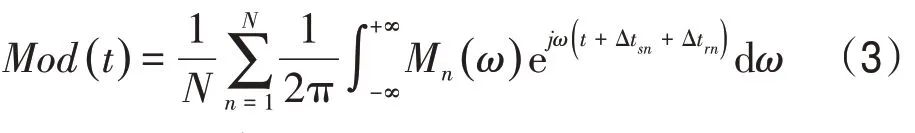
式中：ω为角频率，rad/s。

互相关剩余静校正假设条件之一是炮点与检波点处剩余静校正量是随机分布的，并且在同一个CMP 内的均值为0，即=0，式（5）可简化为

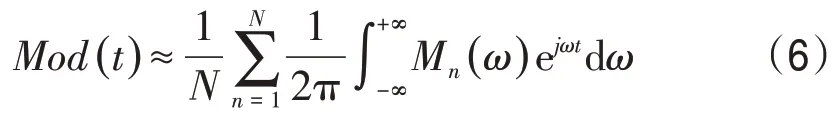
式（6）建立模型道成立的条件是δ2(t) 足够小，而对于确定的地震数据而言，各个炮点、检波点的静校正量是确定的，要使δ2(t)足够小，就必须使角频率ω足够小，又因为静校正量的大小与参与叠加的地震道角频率呈负相关关系，即：静校正量越大，参与叠加的地震道角频率越小。因此，地震波的低频成分产生的模型道更加的可靠，但是仅采用低频成分产生的模型道与该频率成分对应的各地震道进行相关计算，相关函数对低频成分敏感性较差，拾取的时移量误差相对较大。因为获得的各地震道的时移量是逐渐向真实时移量逼近的，剩余时移量与拾取前时移量相比会明显变小，原本不满足式（6）的较高频分量也可以逐渐满足。多尺度分频剩余静校正方法就是在加载剩余静校正量的基础上，选取更高的频率成分进行下一轮剩余静校正计算，以此提高剩余静校正量精度。

多尺度分频剩余静校正方法获取高精度时移量的尺度模式为

多尺度分频剩余静校正的具体步骤（图4）：

图4 多尺度分频剩余静校正步骤Fig.4 Concrete steps of multi-scale frequency division re‐sidual static correction

①确定资料的有效频带范围（FL—FH），根据模型道对资料频率的敏感性程度，采用有效频带内靠近低频端（FL—F1）的数据，进行模型道计算及剩余静校正量分解，获得第1 套由低频模型计算的剩余静校正量M1。

②在加载M1的基础上，重新进行动校速度分析，然后采用有效频带内较高的频率（F1—F2）的数据，进行第2 轮的剩余静校正量计算，获得第2 套剩余静校正量M2。

③同时加载M1和M2，再次进行动校速度分析及剩余静校正量计算，采用有效频带内高频端（F2—FH）的数据，进行第3 轮的剩余静校正量计算，获得第3 套剩余静校正M3，在具体实现过程中，可以依据模型道对于资料频率的敏感性，将频率尺度分得更细。

为试验该方法的有效性，选取松辽盆地达深20井区“两宽一高”采集资料进行测试。该区块资料通过层析静校正之后，浅层波组信噪比较高，连续性更好，利于深层小断裂和储层精细评价，但为了消除中短波长静校正影响，充分利用宽频带、高密度资料的特点，开展了多尺度分频剩余静校正方法。按照低频带（4～35 Hz），中频带（30～60 Hz）和高频带（50～100 Hz）的先后顺序，进行多尺度分频剩余静校正，较好的保护和增强中深层的中高频资料能量，逐步减小校正误差，以满足高密度资料对静校正精度的要求。

通过全频带资料开展剩余静校正后，成像质量虽然得到改进，但是部分区域内成像并不清晰［图5（a）］，通过低频、中频、高频等3 个轮次迭代剩余静校正后，成像得到明显改善，尤其是高频、薄反射层成像更加清晰（如图5 中红色方框所示）。

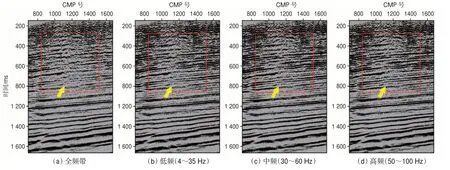
图5 多尺度分频剩余静校正叠加剖面对比Fig.5 Comparison of multi-scale frequency division residual static correction stack sections

通过3 轮次多尺度分频剩余静校正后，剩余静校正量更加收敛。通过低频剩余静校正后，剩余静校正量收敛在半个采样率（采样率为1 ms）的区域占全区的47%，通过中频剩余静校正后，剩余静校正量收敛在半个采样率的区域占全区的62%，通过高频剩余静校正后，剩余静校正量收敛在半个采样率的区域占全区的96%，未收敛在半个采样点的区域主要分布在工区边界处（图6）。

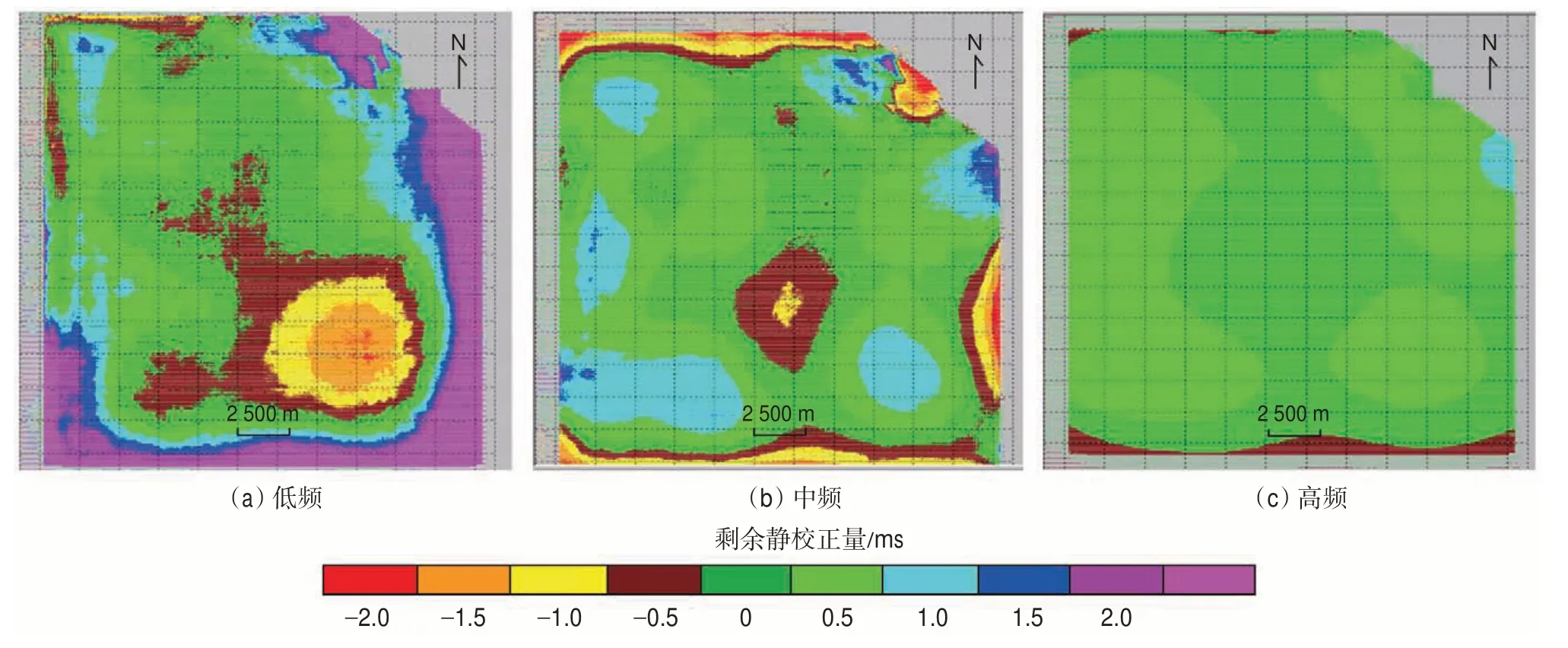
图6 多尺度分频剩余静校正后剩余静校正量对比Fig.6 Comparison of residual statics after multi-scale frequency division residual static correction

1.3 基于共成像点（CIP）道集的时变剩余静校正

在CMP 道集上，采用基于地表一致性剩余静校正时，需要资料有一定的信噪比才能获得准确的动校正速度及高精度的模型道，基于CMP 道集的地表一致性剩余静校正很难彻底消除极低信噪比区的剩余静校正［21-22］。基于CMP 道集的非地表一致性剩余静校正计算方法，结合叠前偏移后共成像点道集信噪比较高的特征，采用一种新的基于共成像点道集的时变剩余静校正思路。该方法不需要满足地表一致性假设，可以动态地对地震道进行校正和叠加，以增强反射波能量。采用该方法计算剩余量时，必须要保证最大时移量不能超过基于CMP道集所用时移量的一半。比如，采用地表一致性剩余静校正时，若采用最大时移量为24 ms，则在CIP道集采用时变剩余静校正的最大时移量不应超过12 ms。由于CIP 道集较高的信噪比，且该方法采用相关算法计算剩余静校正，因此，在一定程度上可以解决部分弱各向异性。

2 高精度组合剩余静校正实现

为了更加有效地提高剩余静校正量的计算精度，进一步提高成像质量，可以融合上述3 种剩余静校正方案，在兼顾计算效率的前提下，尽可能提高剩余静校正量的计算精度。其核心步骤是，先确定适应的空变时窗，然后在各时窗内选择合适的尺度，基于常规地表一致性反射波剩余静校正理论，开展剩余静校正拾取及分解。在极低信噪比区域，通过叠前偏移成像后，在CIP 道集上进行研判，若仍有剩余静校正量残余，则可以采用基于共成像点道集的时变剩余静校正，解决残余剩余静校正量。具体实现思路如下：

①根据地下构造的空间变化趋势，确定不同区域剩余静校正量的计算时窗W1，W2，W3，以及各自的有效成像区域S1，S2，S3。

②在某一计算时窗W1内，确定模型道对频率的敏感性，以划分频率尺度，如以3 个尺度F1，F2，F3为例，首先采用统一的F1尺度内，在空间S1内采用W1时窗，在空间S2内采用W2时窗，在空间S3内采用W3时窗，计算第1 个尺度内的剩余静校正量M1，再采用同样思路，依次采用F2，F3尺度计算与之对应的剩余静校正量M2，M3。

③在CMP 道集加载M1，M2，M3等3 套剩余静校正量开展叠前偏移成像，若在CIP 道集上仍然有剩余静校正量存在，可继续开展基于共成像点道集的时变剩余静校正，消除残余剩余静校正量。

3 实际数据测试

为了测试本文所述组合剩余静校正方法的有效性，选取了柴达木盆地北缘九龙山地区三维资料进行测试。测试区位于柴达木盆地柴北缘东北部，在塞什腾山和绿梁山交汇区，南部与马海古隆起与赛什腾凹陷相接，测试区表层结构复杂，近地表厚度速度变化快，工区逆掩冲断、褶皱发育，地层产状多变，地震波场复杂，且下盘逆掩距离大，断裂带复杂、位置不准，解释多解性强，属于典型的双复杂构造区（图7）。仅采用基础静校正方法和传统剩余静校正，很难彻底解决该区静校正问题。

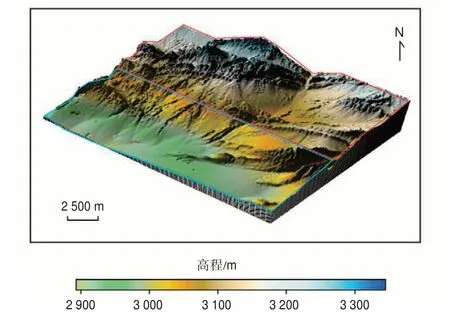
图7 柴达木盆地九龙山高程图Fig.7 Elevation map of Jiulongshan area in Qaidam Basin

从做完基础静校正及常规地表一致性剩余静校正后的叠加剖面［图8（a）］可以看出，不管是在山底隔壁区、山前带还是山顶区域，均没有彻底解决近地表影响。为进一步提高剩余静校正精度，采用本文所述组合剩余静校正方法。

根据地下构造的空间变化趋势以及不同计算时窗测试，最终测试在山底及山前带S1区域（如图7中蓝色方框所示），采用计算时窗为800～3 000 ms（W1）时，其剩余静校正效果较好，在山顶S2区域（如图7 中红色方框所示）采用计算时窗为500～2000 ms（W2）时，其剩余静校正效果较好，单纯采用W1和W2这2 个计算时窗开展空变多时窗融合剩余静校后，效果明显改善［如图8（b）中红色箭头所示］。

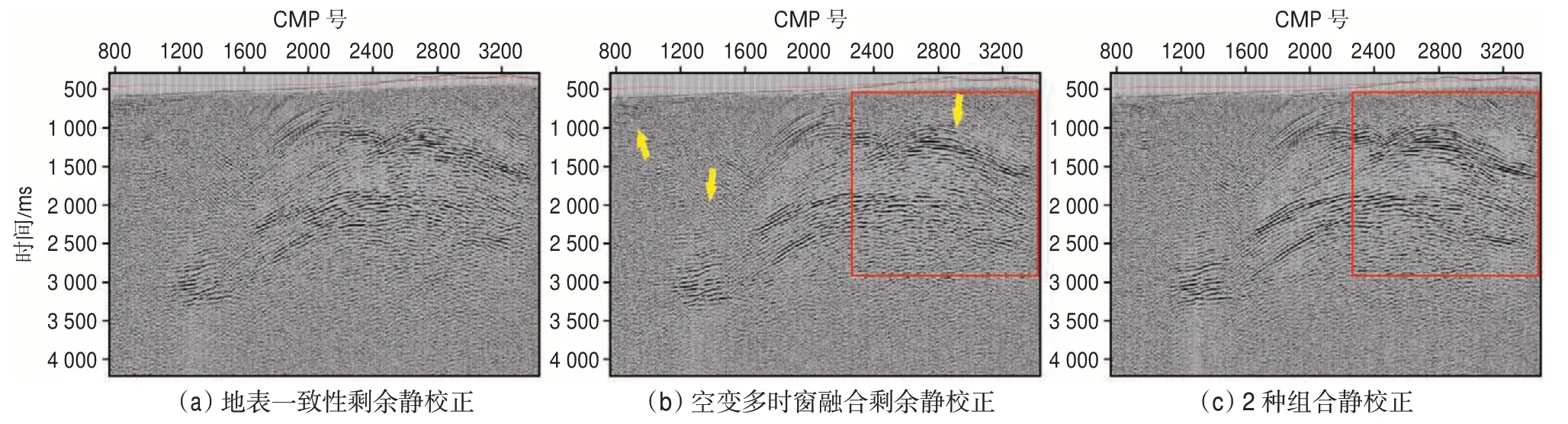
图8 不同方法剩余静校正的叠加剖面Fig.8 Stack sections with different residual static correction methods

在W2区域内，测试了模型道对频率的敏感性，以主频19 Hz 为界，确定了F1（6～19 Hz）以及F2（19～65 Hz）这2 个计算尺度。采用统一的F1尺度内，在空间S1内采用W1时窗，在空间S2内采用W2时窗，计算第1 个尺度内的剩余静校正量M1，再采用统一的F2尺度，在空间S1内采用W1时窗，在空间S2内采用W2时窗，计算第2 个尺度内的剩余静校正量M2，加载2 轮剩余静校正后［图9（c）］效果更好。

应用2 轮剩余静校正后，基本解决了本区剩余静校正问题，剩余静校正残差基本收敛在1 个采样点（±2 ms）以内，叠前时间偏移后，在相对较高信噪比的共成像点道集上，发现在一些极低信噪比区域，仍存在剩余静校正量残余。为彻底解决这一问题，采用基于共成像点道集的时变剩余静校正，在浅层区域采用了6 ms 的时移量，在中深层3 秒目标区附近采用了4 ms 的时移量，既可以解决残余剩余静校正量，又不会破坏目标区的各向异性、裂缝及断层信息，道集一致性更强［如图9 中红色框线所示］。

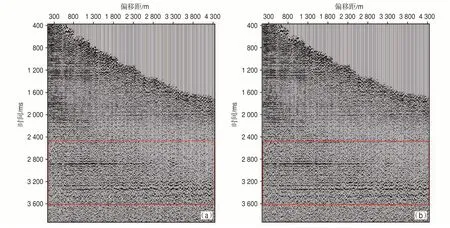
图9 剩余静校正前（a）、后（b）CRP 道集效果对比Fig.9 Comparison of CRP gathers before（a）and after（b）residual static correction

4 结论

（1）在难以准确获得动校正速度的低信噪比、复杂构造区域，根据地下构造的空间展布规律，可以分不同的时窗进行剩余静校正量的计算，在不同的时窗，组合采用多尺度的分频剩余静校正方法，可以获得精度更高的剩余静校正量。

（2）在解决复杂地下构造及低信噪比地区剩余静校正问题时，组合剩余静校正技术在一定程度上具有与非线性反演方法相同的计算效果，同时具有与线性反演方法近似的计算效率。

（3）通过叠前时间偏移或叠前深度偏移后，共成像点道集信噪比得到了很大提高，如果在共成像点道集上仍存在残余静校正问题，可以通过基于共成像点道集的时变剩余静校正方法消除，但不要采用过大的时移量，以免破坏资料的裂缝、断裂等信息。