可压缩Navier-Stokes-Poisson方程的线性稳定性

范焱龙，武瑞丽

(1.四川大学数学学院， 成都610064； 2.四川大学锦城学院, 成都611731)

1 引 言

Jeans不稳定性首先由Jeans[1]于1902年提出.在经典天体物理理论[1]中,因为星际气体十分稀薄, 气体的Jeans不稳定性由如下 Euler-Poisson方程描述：

(1)

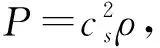
(2)

并考虑其对应线性算子Lλ的特征值问题， 其中λ为系统的控制参数，G(u;λ) 为关于u的高阶项. 若Lλ特征值的实部全部小于0，则系统是线性稳定的；若存在实部大于0的特征值，则系统是线性不稳定的. 此即考察线性算子的特征值βi(λ) 序列(计入重数)是否满足如下稳定性交换准则 (Principle of Exchange of Stabilities)[2-3]：

Reβj(λ)<0,∀j≥m+1

(3)

对于稳态解的线性稳定性来说，研究线性算子Lλ的谱是至关重要的. 当前，对不可压缩流体方程所对应的线性算子谱的研究已经比较完善[2-3]. 近年来，诸多学者对可压缩流体方程对应的线性算子进行了一系列研究. 对线性算子不依赖于参数的情形， Núez[4]和Levitin[5]使用Fourier分析的方法将问题转化成对矩阵的研究， 证明了这类可压缩流体方程对应线性算子的谱由特征值和特征值的唯一有界聚点组成；Kagei等[6-7]研究了可压缩Navier-Stokes方程对应线性算子的谱，并由此得出了稳态解的渐进性质；Brezina 和Kagei[8]对时间周期平行流也做了类似的研究.当线性算子依赖于参数对，Kagei和Nishida[9]研究了可压缩Navier-Stokes方程平面Poiseuille流的线性不稳定性，得到了平面Poiseuille流稳定时Mach数和Reynolds数的关系；王军礼、张兴伟和刘健[10]在文献[8]的基础上研究了平面Couette-Poiseuille流的线性不稳定性，得到了平面Couette-Poiseuille流稳定时Mach数和Reynolds数的关系.

本文对模型(1)进行一些改进，首先不再假设气体是无粘性的； 其次，鉴于星际气体多以等离子体的形式存在，我们在原方程基础上耦合了磁场项，以考察宇宙磁场对平凡稳态解的影响.

2 模 型

本文主要考虑如下的磁耦合可压缩 Navier-Stokes-Poisson (NSP)方程：

其中v，H，μ0和k0分别代表速度场和磁场，真空中磁导率，磁扩散率， 压强p(ρ) 满足多方过程

p(ρ)=αρβ， 1≤β<2，

取无量纲参数

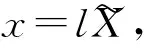
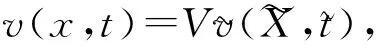
得到如下无量纲模型：

ρ=1,v=0,H=H0=(h1,h2,h3)T

(6)

其中(h1,h2,h3)T表示向量 (h1,h2,h3) 的转置. 为考虑方程稳态解的稳定性，一般的做法是将方程(5)的解写成如下形式

其中u′ 表示扰动. 将上述表达式代入方程(5)并且考虑到φ=Δ-1ρ,得到如下线性扰动方程

(7)

其中线性算子

(8)

另外，质量守恒定律要求密度要满足方程

3 特征值

本节主要考虑 NSP 方程的特征值以及稳定性交换准则，并以此来判断 Jeans 不稳定性何时出现. 在周期边界条件下，考虑空间X和Y如下：

(9)

∀i=1,2,3,n∈Z},

其中ei(i=1,2,3) 是xi方向的单位向量. 定义空间

(10)

其中

Lλu=βu

(11)

注意到周期边界条件允许我们寻找有如下展开式的特征函数u

将上述表达式代入(11)式，得到

Lλu=βu⟺Lλ,kUk=βUk,∀k∈Z3{0}

(12)

其中

(13)

分块矩阵中的子矩阵表示如下：

其中k=(k1,k2,k3)∈Z3{0} 是波数. 直接计算可以得到矩阵Lλ,k的特征多项式D(β)

D(β)=(β+E)(β2+(E+M)β+K)

(β4+C3β3+C2β3+C1β+C0)

(14)

其中

E=4π2η|k|2,M=4π2ν|k|2,

K=4π2(4π2|k|4νη+(k·H0)2),

C0=4π2(4π2|k|2λ2-1)(4π2|k|4νη+(k·H0)2),

C1=4π2|k|2(η+ν)(4π2λ2|k|2-1)+

C2=4π2|k|2(|H0|2+4π2|k|2(ην+

解方程D(β)=0，可以得到

βk,1(λ)=-4π2η|k|2<0,

βk,2(λ)=-2π2(ν+η)|k|2+

βk,3(λ)=-2π2(ν+η)|k|2-

(15)

是Lλ,k的三个负实部的特征值，即 Reβk,j(λ)<0(j=1,2,3). 此外，特征多项式(14)的另外四个根βk,j(j=4,…,7) 是下面多项式的根

f(β)=β4+C3β3+C2β3+C1β+C0

(16)

容易得到Lλ,k有零特征值当且仅当C0=0， 即

(17)

由此可知当λ>1/(2π) 时，对任意k=(k1,k2,k3)∈Z3{0}，Lλ,k不含零特征值,为了确定在λ≥1/(2π) 时没有实部为零的虚根出现，有如下引理.

引理3.1若λ≥λk，则Lλ,k不含任何纯虚特征值.

证明 反证法. 假设当λ≥λk时，Lλ,k至少有一个纯虚特征值,即方程f(β)=0 有纯虚根. 易知f(β) 有纯虚根当且仅当其系数满足

(18)

首先证明特殊情况,即当λ=λk时方程不存在纯虚根. 在此条件下，我们可以得到C0=0. 又因C1>0，所以Lλ,k有纯虚特征值当且仅当C2C3=C1. 但是，直接计算发现C2C3-C1>0.这说明Lλ,k在此情况下没有纯虚特征值.

下面考虑λ>λk的情况. 为了简便，使用记号G=4π2|k|2λ2-1>0. 注意到当k和 |H0| 固定时，(k·H0)2在 0 到 |H0|2|k|2之间取值. 为了方便计算，设 (k·H0)2=x|H0|2|k|2，x∈[0,1]. 若(18)式成立，则有如下关于x的二次方程 Θ(x)=0 成立:

P2x2+P1x+P0=0

(19)

其中

P0=-16π4|k|4·

P1=64π6|H0|2|k|6·

若Θ(x)<0 对任意的x∈[0,1]，G>0 和H0∈R3成立，则(18)式不可能成立，由此导出矛盾. 事实上，当 |H0|=0 时，通过计算可知P2=0，Θ(0)=P0<0，

由此可知Θ(x)<0，∀x∈[0,1].

当|H0|≠0 时，同样有P2>0，Θ(0)=P0<0及

[G2+8π2G|k|2(2π2|k|2(2ν2+(ν+η)·

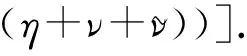
为确定Θ(1)的符号，考虑方程Θ(1)=0，即

其中

注意到

当Ψ±是实数时，Ψ±的符号由 Ψ1控制，也就是说，只有当

又已知当|H0|=0 时 Θ(1)<0，这意味着任意G>0，H0∈R3,x∈[0,1] ，有 Θ(x)[0,+∞)，即(18)式不成立. 进而可知Lλ,k不含任何纯虚特征值. 证毕.

引理3.2对每个k∈Z3{0}，存在一个εk>0,使得下面关于矩阵Lλ,k的特征值的的命题成立:

(i) 存在唯一的m∈{4,5,6,7} 使得对λ≥λk-εk下面的稳定性交换准则成立：

(20)

(ii) 若λ≥λk-εk，则 Reβk,j(λk)<0 对j∈{1，…,7}{m} 成立.

证明 首先证明 (i). 由(17)式和引理3.1 知Lλ,k有零特征值当且仅当λ=λk. 对于特征值βk,i(λ)(i=1,2,3)，由式(15)可知

Reβk,i(λ)<0,i=1,2,3

对λ≥λk成立,则存在m∈{4,5,6,7} 使得βk,m(λk)=0.注意到特征值βk,i(λ)(i=4,…,7) 是由(16)式给出的多项式f(β) 的四个根且m的唯一性可由λ=λk⟹C1>0 得到，且βk,m是方程f(β)=0 的解，所以对方程两边关于λ求导并令λ=λk可得

从而(20)式成立.

Reβk,l<0,∀λ≥λk,

只需要证明当λ=λk且

3|H0|2

(21)

时Reβk,l<0. 注意到当λ=λk时βk,j(λk) 是下面三次方程的零点：

g(β)=β3+C3β2+C2β+C1,

其系数Ci(i=1,2,3) 都为正数，若(21) 式成立，则

g′(β)=3β2+2C3β+C2

(22)

有两个不同的负实根. 这是因为

3|H0|2>0

和三次方程根的判别式保证了g(β)=0 的根都是实和负的.定理得证.

将临界参数λc表示为

即临界 Mach 数为2π. 则由引理3.2，有如下的PES 条件.

定理 3.3对于线性算子Lλ:X→Y，存在唯一的m∈{4,5,6,7} 使得对某个ε>0 和λ≥λc-ε，Lλ的特征值满足如下 PES 条件：

Reβk,j(λ)<0，当j≠m,|k|2=1时，

Reβk,j(λ)<0，当|k|2>1时.

4 结 论