考虑风能捕获的NSV长航时路径规划方法

贾琪，廖煜雷，庞硕，王博，李姿科，张蔚欣

(哈尔滨工程大学水下机器人技术重点实验室，黑龙江哈尔滨，150001)

常规海洋机器人如水面机器人[1](unmanned surface vehicle,USV)、水下机器人(unmanned underwater vehicle,UUV)、遥控潜水器(remotely operated vehicle,ROV)等一般采用燃油或电池作为动力源，航程受制于所携带的有限能源，难以在线补给，故出现了续航力短、作业范围小的弊端，这对于长期的海洋观测[2]、科学研究、情报侦察等仼务来说，存在作业效能低、成本高、覆盖范围小等问题。为满足长期化、网络化的实时海洋观测任务，目前，世界各国纷纷把目光投向研制更大航程、更长航时、更低运维成本的海洋机器人项目中。为了对周围环境的能量加以利用、提高海洋机器人的续航力，各国学者从根源上解决海洋机器人的能源供给问题设计了不同形式的能源捕获装置。

一年四季内风能在海洋上的分布较为广泛。ZHENG 等[3]提出，每年超过80%的时间，海上风的平均功率密度超过50 W/m2，最大为1 600 W/m2。根据美国自主航行器委员会估计[4]，海面风速约为14 m/s，海洋机器人对风能的利用方式也主要集中在利用风力直接推进和利用风能发电2个方面[5]。

世界许多国家相继研制了利用风能驱动的海洋机器人，其中，ELKAIM等[6]研制了风力驱动的无人双体船Atlantis；Harbor Wing 公司[7]设计出配有折叠螺旋桨辅助推进的三体无人帆船HWT X-3；Ocean Aero 公司[8]研制出了装载折叠翼帆并兼具水面航行和水下航行的能力的SubmaranTMS10；RYNNE 等[9]研制了配备热塑性膜包覆翼和太阳能板的WASP；HOOK 等[10]提出了3 种能源混合驱动的海洋机器人方案设计C-Enduro，通过研究和测试各种能源供给，最终选择了由太阳能板、风力发电机和轻型柴油发电机组成的能源供给系统，可供机器人运行3月，且能够支持高达500 W的有效载荷。

中国科学院沈阳自动化所[11]研制了以风力作为航行驱动力，用太阳能为控制系统和传感器供电，可实现“海鸥”号无人帆船长时间连续作业；王健等[12]研制了风能和太阳能复合动力超长续航无人艇系统，通过增加相应模块可升级为海上搜救无人船、长航程无人巡逻艇等；姜权权等[13]研发出采用风光波3 类自然能复合驱动模式的海洋机器人“驭浪者”号(natural energy drive unmanned surface vehicle，NSV)，且该机器人自持力不小于90 d、载荷能力不小于50 W。与国内外现有的风力、纯光伏、波浪、温差等自然能驱动型机器人相比，“驭浪者”的航速更稳定、可控，能量有冗余、更稳健。

搭载风能捕获设备的海洋机器人更应注重风能捕获模型的建立和自主航行中的路径规划问题，国内外学者针对此问题进行了研究。YOU 等[14]结合帆的受力模型和船舶操纵性数学建模小组(ship manoeuvring mathematical model group,MMG)模型，建立了运动模型，为无人帆船的运动控制、路径规划奠定了数学基础。罗潇[15]分析了风帆的空气动力特性原理，通过引入抢风因子，实现了逆风工况下的船舶“之”字型路径换向决策，并且解决了圆弧形帆船迎风换舷时出现的反向回转问题。马冰彦[16]以航速预测程序(velocity prediction program,VPP)为基础进行了不同面积、不同攻角的翼帆面对不同风速、风向时的航行特性分析。MOUSAZADEH 等[17]建立了MORVARID 在风浪流干扰下的动力学模型，规划了考虑风、浪、流的航行路线。PARAVISI 等[18]通过仿真试验模拟了机器人穿越桥梁的风场模型，可用于执行桥梁检查任务。张海妮[19]通过计算流体力学技术(computational fluid dynamics,CFD)仿真计算路径规划中的阻力性能参数，并在考虑海洋风浪流环境、船舶运动性能的情况下进行验证，基本实现了顺风航行，可以用于扫海作业中区域间移动的路径规划。

NIU 等[20]通过考虑风和流对比了胡萝卜跟踪、非线性制导律、纯跟踪和视线法(pure pursuit and line-of-sight,PLOS)、矢量场等4 种路径跟踪算法，仿真结果可用于帮助确定USV 为了有效处理不同任务而需要执行的路径跟随算法。NIU等[21]又根据海流数据结合Voronoi图、可视图和Dijkstra搜索算法规划出无碰撞的节能路径。康梦萁[22]在采用传统的A*算法进行计算的基础上，针对A*算法在长途规划中耗时长的问题提出了算法简单且耗时较短的局部最优法。杜明树等[23]针对A*算法在短途规划中无法应对未知天气预报和风速风向变化较频繁等问题提出速度最优法。DOS SANTOS 等[24]指出帆船除了在高度非线性和恶劣的海洋环境中工作以外，还需要依靠不可预测的风力来推进航行，为了解决这种问题，提出了一种由底层航向控制器和考虑风向的短途路径规划器组成的导航系统，该系统可以使帆船到达其工作环境中的任何所需目标点。SILVA等[25]提出了适用于无人帆船的全局路径规划方法，基于奖励矩阵和根据风向变化的一组动作，采用强化学习方法，避免无人帆船陷入无法获得速度的逆风死区，使无人帆船能够长时间航行，保证了无人帆船的安全性和鲁棒性。

上述文献对多种类型的风帆进行了力学分析，对不同艇体在风环境中的运动响应进行了动力学建模，为利用风帆推进的海洋机器人研究奠定了基础。张海妮[19]在仿真试验中采取的是单一风向，算法缺少复杂风场环境的验证；康梦萁[22]在仿真试验中采用均匀风场，对风向和风速的设置过于简单，并且算法在长途规划中的适用前提是环境中的风向和风速不能变化过快；罗潇[15]进行了外场试验，但试验选择在风向风速较为稳定的湖中，与随机性较大的海洋环境尚存在一定的差距。以上文献仿真试验中风场的建模都没有贴近真实的海洋环境，此处，“驭浪者”号NSV采用升力型风力发电机，与单纯采用风帆推进的机器人不同，其风力发电过程中航行阻力小，航向操纵更具灵活性，拓展区域更广，并能针对特殊区域进行精细化观测[26]。因此，需要针对海上风力发电机的能源捕获、机器人长航时的路径规划策略进行进一步研究。

本文以“驭浪者”号NSV 为研究对象，针对“驭浪者”在海洋风场中的路径规划问题进行探讨。首先介绍地理环境和海洋风场环境的建模方法，提出海洋环境能量扩展树的概念并结合NSV风能捕获模型构建海洋环境能量集合；然后，通过分析NSV 风能捕获特性，提出适合NSV 海洋风场中的路径规划方法Wind_A*算法；最后，通过2种特殊风场环境和1种真实风场环境对Wind_A*算法与传统A*算法进行仿真对比试验，验证所提算法的有效性。

1 考虑风能捕获的Wind_A＊算法设计

1.1 真实海洋风场可视化建模

在机器人学中，地图的表示方法被分成4 类，分别为特征地图、拓扑地图、栅格地图和直接表征法。栅格地图是机器人对环境描述最常见的方式，即将环境划分成一系列栅格，其中每一栅格给定一个可能值，表示该栅格被占据的概率。它最早由ELFES[27]提出，在火星探测车上得到运用，其本质是一张位图图片，但其中每个“像素”表示实际环境中存在障碍物的概率，它最接近人类认知的地图。本文采用栅格地图构建全球真实海洋风场环境。

海洋和陆地的建模通过提取WGS-84世界大地坐标系中海岸线坐标对可航区域和禁航区域的划分。海洋风场的数据信息来源于全球海洋资料同化系统(global ocean data assimilation system，GODAS)，该系统由国家环境预报中心(national centers for environmental prediction,NCEP)构建；NCEP 隶属于美国联邦政府的海洋大气总署(national oceanic and atmospheric administration,NOAA)，是美国国家级的气象业务主管机构。GODAS 依赖于全球海洋观测系统的连续实时数据。该项目将提供常规的海洋监测产品，并由气候预测中心(climate prediction center,CPC) 与NOAA 全球海洋监测与观测(global ocean monitoring and observation,GOMO)合作实施。该系统通过采集散布在世界各地海洋中的传感器监测数据，来实现对海洋环境的系统监测，数据真实，可靠性强。根据陆地和海洋的坐标数据，调用GODAS数据构建了图1所示的可视化模型。

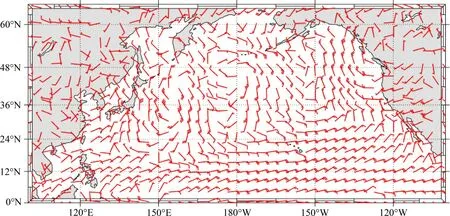
图1 北太平洋风场模型[28]Fig.1 Model of north pacific wind field[28]

1.2 海洋环境能量扩展树

常规海洋机器人通常仅需考虑路径的消耗，就能完成规划路径的搜索；NSV 具有多种海洋能量捕获设备，在考虑路径长度的同时还需兼顾能量的捕获。本文仅针对风能捕获设备的能量捕获提出路径规划指导，忽略其他设备的能量捕获影响。

图2所示为海洋环境能量扩展树概念图。由图2可见：NSV不同路径与树的不同枝丫类似，该栅格内的风能由NSV 的航行方向决定，与果子结在枝丫上类似，不同的枝杈上结有不同能量的果实。NSV 的目的就是从树的某处到另一处，尽可能沿着树枝在兼顾路程的基础上尽可能采撷到高能量的果实，即实现能量捕获最优。

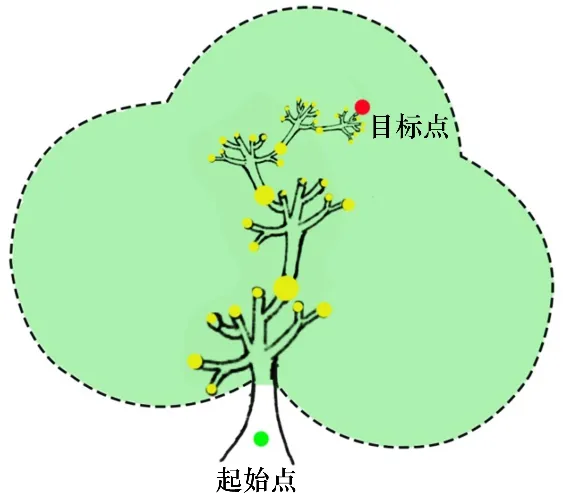
图2 海洋环境能量扩展树概念图Fig.2 Concept map of marine environmental energyexpansion tree

NSV 在跨越到邻近的栅格时将面临不同的方向，每个栅格内的环境风向也不同。对于自然能驱动机器人而言，步入不同的栅格就意味着按不同的行进方向运动。每个栅格不同的行进方向的实时风能捕获效果都不同。

风力发电机搭载在NSV 甲板上方，当NSV 航行时，风力发电机的发电效果实际受视风速度影响，视风速度由船风速度和真风速度共同决定，如图3所示。船风速度vwind_s的方向与NSV 航向相反，大小与航速相等，真风速度vwind_t是海风相对大地坐标系的矢量表示，视风速度vwind_a为真风速度和船风速度的合成速度矢量，其计算方法见下式：

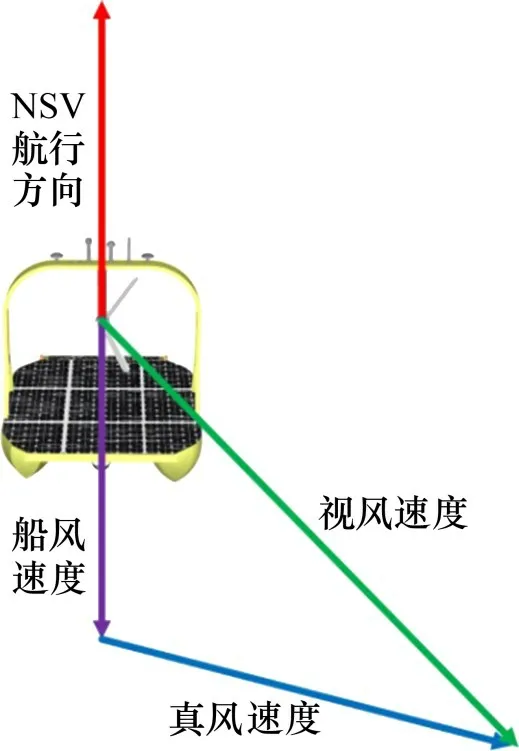
图3 视风示意图Fig.3 Schematic diagram of apparent wind

因此，即使在海风恒定的环境中，风能的捕获量受NSV的航向和航速影响。

本文将NSV的移动方向分为如图4所示的8个方向，根据风力发电机的风速−功率关系计算出不同方向的潜在能量，从而完成海洋风场环境的能量树建模。

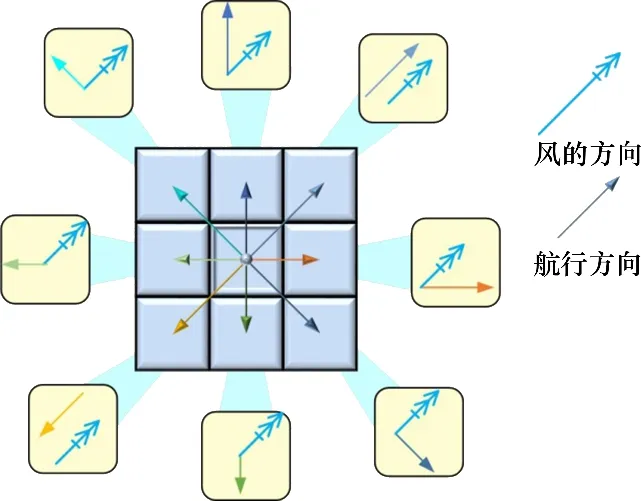
图4 NSV的可行航向Fig.4 Feasible course of NSV

1.3 自然能驱动机器人风能捕获模型

自然能驱动机器人所搭载的风能捕获系统，采用风力发电机利用风力带动风车叶片旋转，再通过增速机提升旋转速度，来促使发电机发电，再经由NSV 专用的能源管理设备将电能存储在蓄电池中，作为NSV 的能源补给。风力发电机的发电功率与风速的关系通过风洞强制测试试验可获得，如图5所示。由图5可知：NSV艇载风力发电机的发电功率曲线走势近似呈线性变化，将其进行线性拟合可得

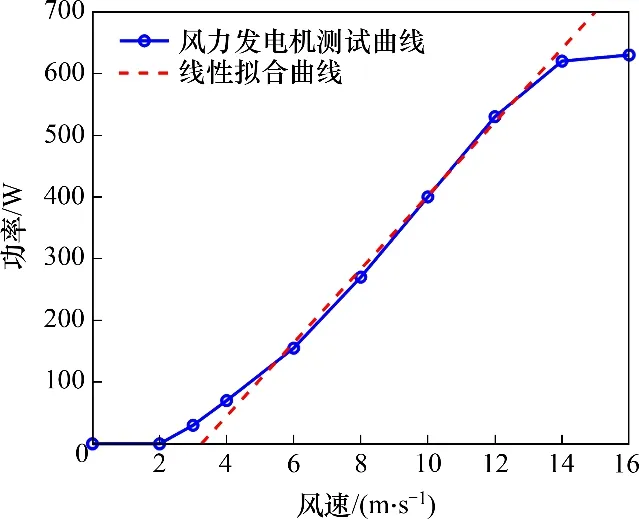
图5 风力发电机测试曲线和拟合曲线Fig.5 Wind turbine test curve and fitting curve

式中：PWind_Turbines为风力发电机在海洋风场环境中的发电功率；ω0为拟合函数常数项；ω1为拟合函数一次项系数。

将风能捕获系统装载在NSV上，随风速增大，NSV 将捕获更多能量，但同时也将NSV 面临更大的风阻，通过CFD 技术计算NSV 在不同风速下的纵向受力，得

式中：Rwind为NSV 纵向受到的风作用力；θ∈(0,π)，为视风速度和船首的夹角。

NSV 为了保持巡航航速，推进器需提高一定推力来克服风阻的干扰，推进器在不同推力下的功率可通过推力试验获得，并进行多项式拟合得

式中：x为推力；fFP(x)为推进器功率。

Pthruster_w为NSV 在风中保持巡航速度的输出功率。考虑风阻增大对NSV推进功率的影响，有

式中：Rship为NSV在无风环境中保持巡航速度的静水阻力。

因此，风能捕获的能量输入功率为

式中：Psum(wind_input)为风能捕获系统针对整个NSV系统的能量总输入功率；Pthruster为在无风环境中保持巡航速度的输出功率；τ为电能存储转化系数。

1.4 考虑风能捕获的Wind_A＊寻优函数设计

A*算法由HART 等[29]提出，该算法兼顾了Dijkstra 算法和广度优先算法的优点，既能保证搜索到最优路径，又能通过启发式的搜索，降低搜索空间，缩短计算时间，广泛应用于机器人在栅格化的地图中的路径规划。

典型的A*算法一般在路径规划过程中设计2个集合，其中，一个为Open 集合，用于存放已经求取估值但仍未被扩展的节点，另一个为Closed集合，存放已被扩展的无须关注的点。A*算法通过估价函数f(n)来确定搜索的方向和下一个节点的位置，一般情况下根据机器人类型或任务需求，机器人的搜索方向分为N，S，W 和E 共4 个方向或N，NE，E，SE，S，SW，W 和NW 共8 个方向，当前节点n到下个节点n'的路径需要根据估价函数f(n)分别计算节点x周围节点代价的最小值来确定。A*算法从起点开始搜索，直到目标点落入Closed 集，然后将Closed 集合中所有的节点连线，该连线即为机器人任务的规划路径。A*算法的估价函数为

式中：g(n)为机器人从起始点到当前节点的实际代价；h(n)为当前节点距离目标节点的估计代价，也称为启发代价。本文根据NSV 的航行特点和风能捕获需求，基于A*算法，提出Wind_A*算法，该算法通过计算NSV 从起始点到当前节点间风能捕获系统输入和推进系统、电控系统输出的差值能量作为NSV 系统的总消耗能量，通过当前节点和目标点的启发能量来控制路径的搜索方向，从而得到考虑风能捕获的NSV长航时路径。

1.4.1 考虑风能捕获的能源消耗函数

本文着重关注风能捕获，没有考虑其他海洋环境(光、波浪、流等)的影响，NSV在海洋风场环境中能源的输出为保证各传感器、控制系统和推进器正常工作的能量消耗；能源的输入为风能捕获系统产生的电能，因此，NSV 在海洋风场中的能量消耗函数gw(n)为

式中：ge_cost(n)为NSV各传感器和控制系统等电子元器件消耗的能量；gt_cost(n)为推进器消耗的能量；gwind(n)为NSV风能捕获系统的能量输入。

NSV 的巡航速度是固定的，NSV 在每个栅格的可航行方向为8 个方向，假设NSV 在栅格内朝N，S，W 和E 方向的航行时间为dt；朝NE，SE，SW 和NW 方向的航行时间为则NSV 在每个栅格内消耗的能量为(Pthruster+Pe)⋅dt(其中Pe为电子元器件的消耗功率)。NSV 在每个栅格内的能量输入为[τPWind_Turbines-(Pthruster_w-Pthruster)]⋅dt。综上所述，NSV在风场环境下的能源消耗函数为

式中：Ethruster为NSV在每个栅格内的推进器能量消耗；Ewind_input为NSV在每个栅格内的风场能量输入。

1.4.2 Wind_A*的能耗启发函数

h(n)是估价函数中的启发项，这是A*算法相较于Dijkstra 算法的优势所在，启发函数在路径搜索过程中能有效地抑制无用空间的搜索，达到减小搜索空间，使算法快速收敛。本文采用曼哈顿距离的思想构建启发函数，它计算的是能量扩展空间中NSV 当前位置到目标位置之间南北方向和东西方向潜在能量之和，这个能量是模糊的，旨在提高算法的搜索速度，即

式中：n(x)和n(y)为当前节点的坐标；G(x)和G(y)为目标节点的坐标；D为启发系数，将启发距离转化成启发能量，用来配合消耗函数更好地对搜索节点进行估价。Wind_A*算法的流程图[30]如图6所示，其中c(ni,ni+1)表示相邻节点间NSV的推进器等设备的能量消耗减去风能捕获设备捕获到的能量，即栅格间的能量总消耗。

图6 Wind_A*算法流程图Fig.6 Flow chart of Wind_A*algorithm

2 算法仿真试验研究

仿真试验中软件平台为Windows，硬件平台的处理器为Inter Core i7-4710HQ(主频2.5 GHz)、运行内存16 GB。根据1.3节的分析，可知当NSV 的巡航速度为1.5 m/s 时，巡航功率为600 W，分别针对简单变化风场、螺旋变化风场和真实风场进行仿真试验验证。

2.1 简单变化风场环境的仿真对比

简单变化风场仿真试验建立在网格分辨率为100×100 的栅格地图上，NSV 的起始点位置为(5，50) m，目标点位置为(95，50) m，网格的单位间距为1 852 m。为了测试Wind_A*算法的有效性，将栅格地图上的表面风场设置为左半部分南风，右半部分北风，风速均为12 m/s，其中，图7和图8所示分别为传统A*算法和Wind_A*算法的路径规划图，表1所示为仿真能耗。图7和图8中，红色区域为探索区域，绿色箭头表示风的方向和速度，黑色线为路径。

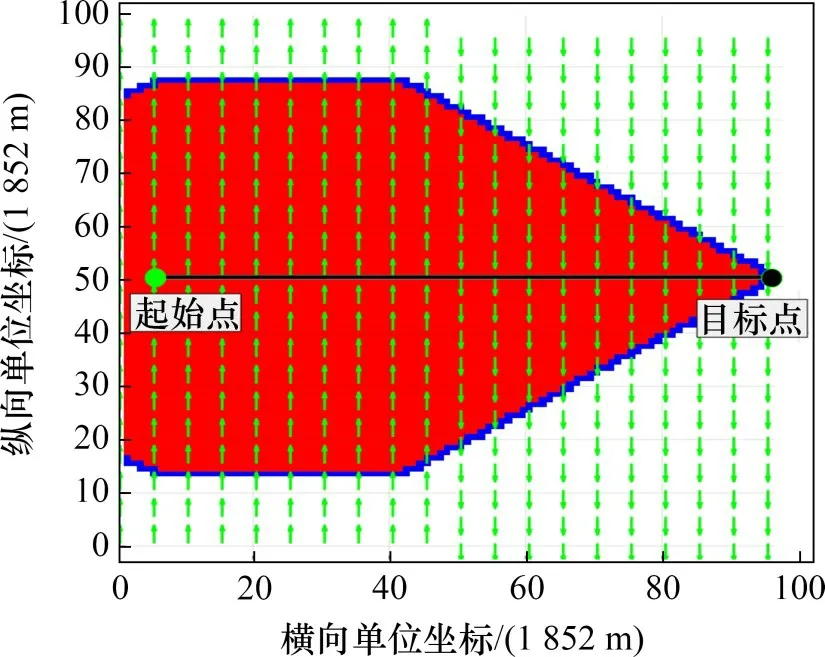
图7 简单变化风场中传统A*算法规划路径Fig.7 Planning path of traditional A*algorithm in simple change wind field

图8 简单变化风场中Wind_A*算法规划路径Fig.8 Planning path of wind_A*algorithm in simple change wind field

从图8可以看出：面对南向来风，NSV为了捕获更多的风能选择向右偏转，当风向转为北风时，NSV又向左偏转，向着目标点驶去。从表1可以看出：与传统A*算法相比，Wind_A*算法需要探索更多的空间，这是由于栅格地图中存在更高能量的潜在路径需要探索，即存在更低能耗的路径。虽然，Wind_A*算法规划出的路径更长，但在此恒定风场环境中可减少能耗9.93%。

表1 简单变化风场中算法仿真对比结果Table 1 Comparison results of algorithm simulation in simple change wind field

2.2 螺旋变化风场环境的仿真对比

螺旋变化风场仿真试验建立在网格分辨率为100×100 的栅格地图上，NSV 的起始点位置为(5，50) m，目标点位置为(95，50) m，网格的单位间距为1 852 m，栅格地图上的表面风场设置为逆时针旋转的风场，风眼位置在(50，50)m附近，最大风速可达14 m/s，其中，图9和图10所示分别为传统A*算法和Wind_A*算法的路径规划图，表2所示为仿真能耗，图9和图10中，红色区域为探索区域，黄色箭头表示风的方向和速度，箭头越长，表示风速越大。

表2 螺旋变化风场中算法仿真对比结果Table 2 Comparison results of algorithm simulation in spiral wind field

由图9可知：风眼位置风速最高，以风眼为中心周围风速随距风眼的距离增加，风速逐渐减小。图9和图7所示路径一样，由于采用传统A*算法，环境风场的变化并没有影响规划的路径。图10中NSV的路径可根据风眼的位置分为3个阶段。

图10 螺旋变化风场中Wind_A*算法规划路径Fig.10 Planning path of wind_A*algorithm in spiral wind field

第一阶段：靠近风眼，由于起始点距离风眼较远，风速较小，NSV的Wind_A*规划路径与图9的初期路径相同。

第二阶段：驶进风眼，由于风眼附近的高风速，导致NSV 为了捕获更多的风能，在权衡路程消耗的基础上围绕风眼航行1周才驶离风眼区域。

第三阶段：远离风眼，随风速降低，附近其他方向的捕获能量减少，NSV 的Wind_A*规划路径与图9的末期路径相同。

图9 螺旋变化风场中传统A*算法规划路径Fig.9 Planning path of traditional A*algorithm in spiral wind field

在螺旋变化的风场环境中，Wind_A*算法规划出的路径比传统A*算法规划出的路径减少能耗9.27%。假设NSV 结构设计具备台风中航行能力，通过螺旋变化风场仿真试验可知，NSV 在有效捕获风能的情况下，还能环绕风眼中心航行，为台风、热带低压气旋中心的气象数据观测任务提供了一种技术手段。

2.3 真实风场环境的仿真对比

真实风场环境仿真试验建立在0°纬线至北纬30°、东经90°至东经135°的栅格地理图中，这片区域的环境具有典型性，包括岛屿、海峡等复杂地形元素和气旋、季风等多种气象要素。NSV 的起始点位置为27.5°N/122.4°E，目标点位置为8.8°N/94.1°E，网格的单位间距为11 112 m。

为了验证Wind_A*算法在真实风场环境中的有效性，通过提取NOAA 的GODAS 数据，假设NSV 所到之处的风场环境都是已知的，且仅考虑风场的空间变化，忽略其时变性，构建了如图11(b)所示风场模型。图11和图12所示分别为传统A*算法和Wind_A*算法的路径规划图，图11(b)和图12(b)中采用气象图中的风矢表示风的大小和方向。风矢由风向杆和风羽2部分组成，风向杆指出风的来向，风羽分别用长划线、短划线、与风三角组合的方式表示风速。表3所示为真实风场中不同算法的能耗对比。

表3 真实风场中算法仿真对比结果Table 3 Comparison results of algorithm simulation in real wind field

从图11和图12可以看出：在真实的风场环境中，由于大尺度中的季风环流方向和NSV 的计划航向有契合的部分，考虑风的Wind_A*算法比传统A*算法的探索空间更少。在北纬12°以北区域，由于风速较小，传统A*算法和Wind_A*算法规划出的路径几乎一致，在北纬12°以南区域，风速开始增大，Wind_A*算法规划出的路径使NSV 向东南方向偏转，以获得更多的风能；进入马六甲海峡后，受地形的限制，2 种方法规划出的路径一致。在真实的风场环境中，Wind_A*算法规划出的路径比传统A*算法规划出的路径减少能量8.54%。

Wind_A*算法搜空间通常较传统A*算法更加广阔，如图7～10 所示。但由图11和图12可知，Wind_A*算法探索空间明显减小，其根本原因是传统A*计算消耗函数时，考虑的仅为欧式距离，该项是标量项；Wind_A*算法包含了风能捕获系统的输入能量，该系统项的主要影响因素是视风速度，视风速度是由真风速度和船风速度共同决定的矢量，当视风速度方向指向目标点时，风能捕获系统的输入能量在消耗函数中能起到加速搜索的效果。

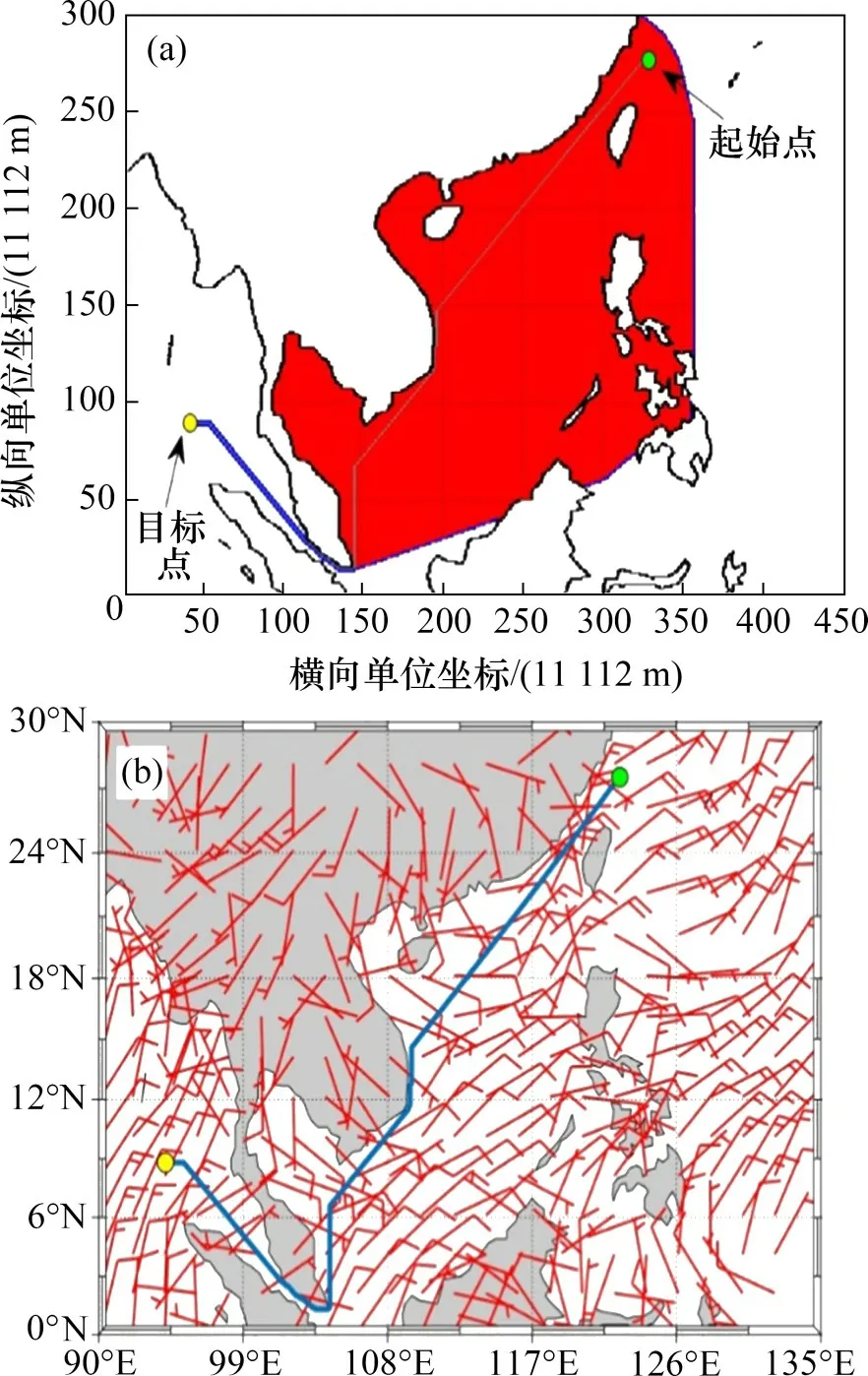
图11 真实风场中传统A*算法规划路径Fig.11 Traditional A*algorithm planning path in real wind field

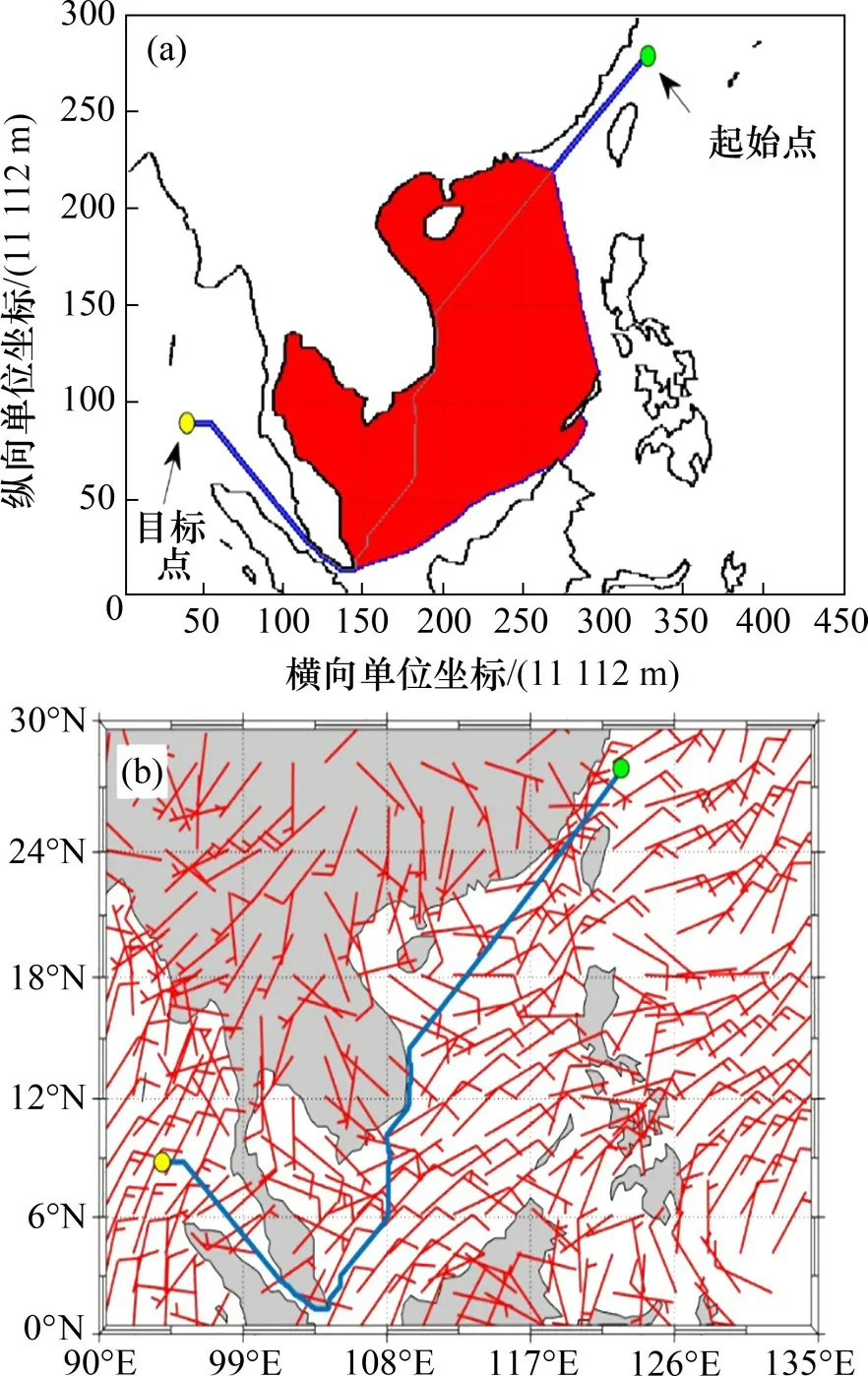
图12 真实风场中Wind_A*算法规划路径Fig.12 Wind_A*algorithm planning path in real wind field

综合上述仿真对比试验可知，Wind_A*算法可在真实的海洋风场环境中规划出无碰撞的安全路径，并且在充分考虑风能捕获和自身航行能量消耗的基础上对航线进行有效修正。与传统A*算法相比，Wind_A*算法虽然在某些工况中探索区域较大，但该算法总能规划出比传统A*算法能耗更小的路径，所提算法能充分应用风能捕获设备，进而有效提升NSV的续航力。

3 结论

1)无论是简单变化风场、螺旋风场还是真实的海洋风场环境，Wind_A*算法都能规划出比传统A*算法更节能的航线，3种风场环境能耗分别减少9.93%，9.27%和8.54%。所提算法规划出的路径能有效增加NSV 对风能的捕获量，从而提高NSV的续航力。

2)Wind_A*算法的评价函数需要通过设置合适的启发系数才能完成路径搜索，该启发函数仍需完善；此外，NSV 可搭载多种能源捕获设备，考虑多设备综合捕获能源对航线规划的耦合影响也需进一步研究。