基于随机遗传算法优化BP神经网络的工业机器人整机性能评估模型
叶伯生,谢鹏,张文彬
(华中科技大学机械科学与工程学院国家数控系统工程技术研究中心,湖北武汉,430074)
随着工业机器人应用领域越来越广泛[1],国家对于工业机器人产业布局与加强竞争力的重视程度越来越高[2]。学者们重点研究零部件和工况条件对整机性能的影响规律[3−4],一方面,可以准确评估工业机器人的整机性能,另一方面,可以科学生产不同性能的工业机器人,高效、高精、可靠地应用至各种场合。
整机性能评估方面,目前通常基于激光跟踪仪[5−7]等测量设备,使用性能评价系统软件[8−9]来完成。然而,测量设备与评价系统被国外垄断,价格昂贵,且不能对未完成装配的工业机器人进行性能预测评估。在整机性能影响规律的研究方面,目前通常基于常规的实验研究法即进行大量测试实验[10],获取一定数量的测试数据来进行绘图分析,从而得到特定参数对特定性能指标的影响规律。但是,工业机器人是一个非线性、多变量的控制对象[11],是由伺服驱动器、减速器、控制器和传感器等众多核心零部件组成的复杂系统[12−15],同时,其整机性能又受到了负载和速度等工况条件的耦合影响,诸多影响条件极大地限制了实验研究法的可执行性及准确性。
本文针对工业机器人整机性能评估指标及影响因子多、影响关系耦合性强和工况条件多变等实际问题,通过对核心零部件性能指标、工况参数与整机性能评估参数的数据进行训练学习,提出一种基于遗传算法优化BP神经网络的工业机器人整机性能评估模型,以期实现对整机性能的评估预测。
1 整机性能评估模型分析及建立
1.1 模型输入/输出参数
为了提高工业机器人整机性能评估模型的准确度与可靠性,必须在模型构建之前确定合理的参数。工业机器人主要由减速器、伺服电机和控制器等核心零部件组成,并且在工作过程中整机性能通常受到工况条件的影响,因此,模型的输入,输出参数主要考虑表1中指标。

表1 模型输入/输出参数Table 1 Model input/output parameters
整机性能指标方面,工业机器人的运动性能是表征其整机性能最重要的指标之一,在GB/T 12642—2013“工业机器人性能规范及其试验方法”[16]中,有14 项工业机器人整机性能指标被确立为国家标准,然而,目前大部分工业机器人厂家及用户并不关注国家标准中规定的所有性能指标。受到重点关注的整机性能指标[17]主要是位置准确度、位置重复性、轨迹准确度和轨迹重复性等。
1.2 基于BP神经网络的整机性能评估模型
1.2.1 BPNN结构设计
减速器、伺服电机、控制器与工况条件等众多因素共同对工业机器人整机性能产生强耦合性影响,BP 神经网络在解决这种复杂非线性模型的问题时有很好的效果[18],为了避免遗漏潜在的性能影响链,充分挖掘性能影响关系,先在输入层之后设置一层隐含层进行初步计算,在此之后再设置一层隐含层以完善处理,形成双隐含层结构,并将其中所有神经元设置为全连接,如图1所示。

图1 BPNN结构设计示意图Fig.1 Schematic diagram of BPNN structure design
1)输入层。整机性能评估模型的输入参数为扭转刚度、空程、传动效率、传动误差、启动扭矩、背隙、正反转速差率、转矩波动系数、转速波动系数、系统效率、温升、电气时间常数、轨迹平滑、准确到位、标定与误差补偿、系统最快响应时间、循环扫描时间、I/O模块响应时间、工作速度和工作负载,共计20 个。因此,BPNN 中为输入层设置20 个神经元,分别用于接收上述参数样本值。
2)输出层。整机性能评估模型的输出参数为位置准确度、位置重复性、轨迹准确度和轨迹重复性,共计4 个。因此,BPNN 中为输出层设置4个神经元,分别用于输出上述参数的预测评估值。
3)隐含层。为了维持影响因子在传递链中的层级递进关系,双隐含层神经元个数保持一致,具体数值结合式(1)与参数调整机制来确定。

式中:q,n和m分别为隐含层、输入层和输出层的神经元个数;a为常数,取值范围为[1,10]。
由式(1)可得q取值范围为[6,15],接着以隐含层神经元数量为横坐标、模型得分为纵坐标绘图,如图2所示。由图2可知:当隐含层神经元个数初始增加时,模型得分大幅度提高;而前者增加至5左右时,后者虽仍呈递增趋势,但速度开始变得缓慢。结合调参过程图与经验式计算结果,隐含层神经元个数设置为10。

图2 BPNN关于隐含层神经元数量的调参过程Fig.2 BPNN parameter adjustment process about number of hidden layer neurons
4)权重与阈值。减速器、伺服电机、控制器与工况条件中各参数对整机性能的影响重要性程度尚且未知,因此,BPNN中所有神经元初始权重与阈值暂且设置为(0,1)之间的随机数。
5)激励函数。工业机器人是由众多部件组成的复杂系统,其整机性能的内部影响机制绝非简单的线性关系,性能评估模型也势必伴随大量计算及时间开销。因此,为了使得BPNN具备非线性映射能力,降低计算量,提高收敛速度,将其神经元激励函数设置为ReLu函数[19],如式(2)所示。

6)损失函数。位置准确度、位置重复性、轨迹准确度和轨迹重复性等性能评估指标都是连续值,由此可见,工业机器人整机性能评估属于预测回归问题。因此,BPNN中损失函数设置为均方误差[20]。

式中:EMSE为均方误差;yi为真实数据;y′i为预测数据;N为样本个数。
7)权重优化器。本文工业机器人整机性能及其影响因子数据集样本量较少,考虑到模型训练效果与收敛速度,BPNN中权重优化器选择使用LBFGS(large Broyden Fletcher Goldfarb Shanno)。
双隐含层全连接神经网络结构具有较强的非线性映射能力,但还需要代入工业机器人性能数据集,使用误差逆传播算法完成训练学习,从而实现工业机器人整机性能预测评估。
1.2.2 遗传算法优化
由于模型输入参数对整机性能的影响重要性程度未知,BPNN 的初始权重与阈值为(0,1)范围内的随机数,可能导致均方误差损失函数陷入局部最小,降低其对于整机性能指标的预测评估准确度。因此,考虑到遗传算法在多参数寻优过程中具备优良的启发式搜索能力[21−22],本文进一步使用遗传算法对BPNN 权重与阈值的初始化进行优化,使其尽可能逼近全局最小[23−24],算法流程图如图3所示。

图3 基于遗传算法优化的BP神经网络流程图Fig.3 Flow chart of optimized BP neural network based on genetic algorithm
1)运行参数初始化。对遗传算法的运行参数进行初始化,参数包括:种群中个体总数N,交叉概率Pc,变异概率Pm,遗传进化总代数G,初代种群Pop(0)和当前种群代数i。
2)种群初始化及个体编码。对初代种群进行初始化,在(0,1)范围内随机生成N组神经网络权重与阈值,将其作为初代种群中的个体;接着对所有个体进行实数编码,编码长度为
式中:L为神经网络中权重与阈值的总个数。
编码格式如图4所示。

图4 遗传算法个体编码格式Fig.4 Genetic algorithm individual coding format
3)种群适应度评价。将适应度评价函数设置如式(5)所示,

式中:f为个体的适应度。
通过式(5)计算种群中所有个体的适应度,适应度可反映个体的利用率,其值坐落于(0,1)范围内,适应度越大,说明个体越优,越值得使用。
4)选择操作。使用轮盘赌法[25]进行选择操作,从种群中挑选出2个个体,概率为

式中:P为每个个体被选中的概率。
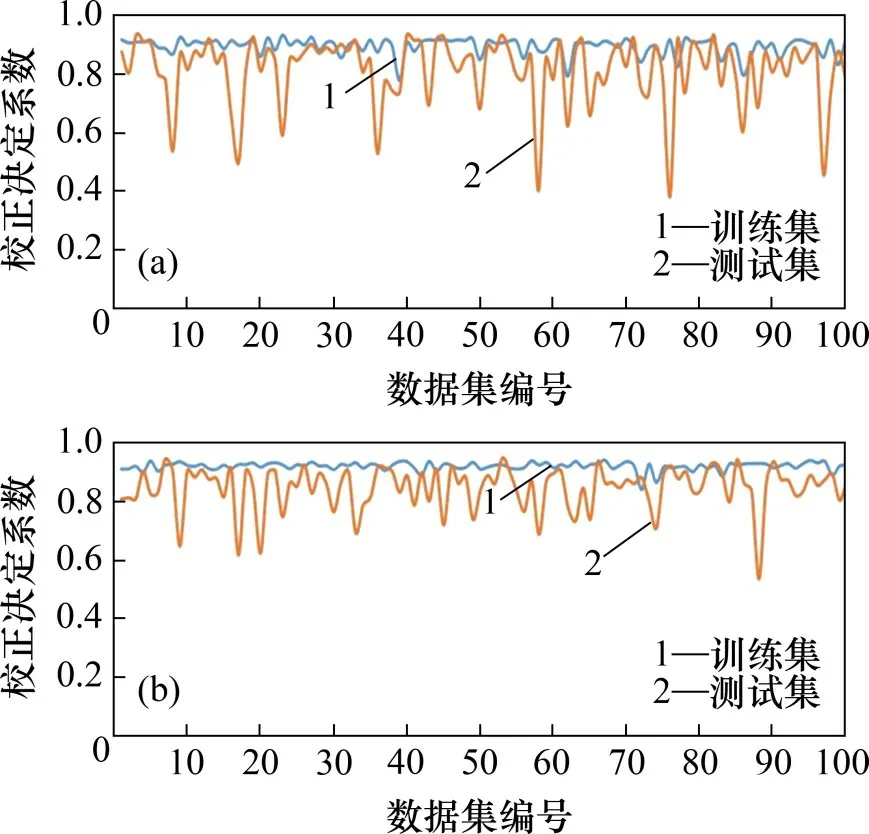
5)交叉操作。使用随机交叉法进行交叉操作,示意图如图5(a)所示,由5(a)可见:先在(0,1)范围内随机生成交叉判断因子P′c,当P′c 6)变异操作。使用随机变异法进行变异操作,如图5(b)所示,由图5(b)可见:先在(0,1)范围内随机生成变异判断因子P′m,当P′m 图5 遗传算法基因操作示意图Fig.5 Schematic diagram of genetic algorithm genetic manipulation 7)子代种群。无论被选中的2个个体是否执行交叉或变异操作,都将其二者加入至下一代种群,若下一代种群个体数目还不及N,则继续执行变异操作;若下一代种群个体数目达到指定要求,则返回第3步对其进行种群适应度评价。 当最高适应度的权重与阈值达到预期效果或迭代次数达到遗传进化总代数时,停止循环迭代,将当前最优个体输出给BP神经网络,进而在遗传算法优化后的权重与阈值基础上完成神经网络训练学习。 将校正决定系数作为指标对模型进行拟合效果分析, 式中:为校正决定系数;p为属性特征数量;R2为决定系数。校正决定系数取值范围为(0,1),值越大说明模型拟合效果越好。 通过10 次10 折交叉验证获取不同的100 份训练集与测试集,用于模型训练与测试,记录校正决定系数并绘图如图6所示。从图6可见:BPNN整机性能评估模型明显存在多次校正决定系数得分低于60%的情况,而经过遗传算法优化后几乎未出现极低分;后者在训练集上的表现虽稍有一定波动,但比前者更稳定;后者在测试集上的拟合效果相对于前者更好,但在不同数据集上的表现差异仍然较大,且大部分得分都只算中等偏上水平。总体而言,遗传算法优化能够明显防止BPNN整机性能评估模型陷入局部最小,其模型泛化能力也较强。 图6 遗传算法优化前后BPNN整机性能评估模型拟合效果Fig.6 BPNN machine performance evaluation model fitting effect before and after genetic algorithm optimization 搭建工业机器人性能测试实验平台及核心零部件性能测试实验平台。实验平台包括六轴工业机器人、机器人控制柜、Leica 激光跟踪仪、伺服电机及减速器安装架和传感器等。通过实验平台对工业机器人整机及其核心零部件进行性能测试,共计获取36 份样本,将其作为验证集代入整机性能评估模型中,得到相应的整机性能预测评估值。本文以整机性能中位置准确度为例对实验的验证过程进行说明。 图7所示为模型预测效果与预测误差分布。由图7(a)可见:模型对于样本的预测值大多数都在样本真实值处上下浮动,并且预测数据基本能够拟合真实数据曲线,这表明模型对未知新样本具有良好的预测评估能力。为了更可靠地验证模型的泛化能力,计算并汇总其对于36 个样本的预测误差,如图7(b)所示。由图7(b)可见:模型对于新样本的预测误差总体分布正常,几乎未出现极端异常值,这说明模型对于样本的预测数据可靠性较高。模型的预测误差相对集中,位置准确度绝对误差大部分坐落于[0.085,0.125],最大误差为0.131 mm。因此,模型总体而言在实际应用中是有效的,能够较准确地对整机性能实现预测评估。 图7 模型预测效果与预测误差分布Fig.7 Prediction effect and prediction error distribution of the model 1)BPNN整机性能评估模型在测试集中存在多次校正决定系数得分低于60%的情况,而经过遗传算法优化后的BPNN整机性能评估模型几乎未出现极低分;后者在训练集和测试集上的表现较前者更优异。遗传算法优化能够明显防止BPNN整机性能评估模型陷入局部最小,导致模型泛化能力更强。 2)以工业机器人位置准确度为例,建立的整机性能评估模型的预测值在样本真实值处上下浮动,位置准确度绝对误差大部分坐落于[0.085,0.125],最大误差为0.131 mm,未出现极端异常值,表明建立的模型在实际应用中是有效的,能够较准确地对整机性能实现预测评估。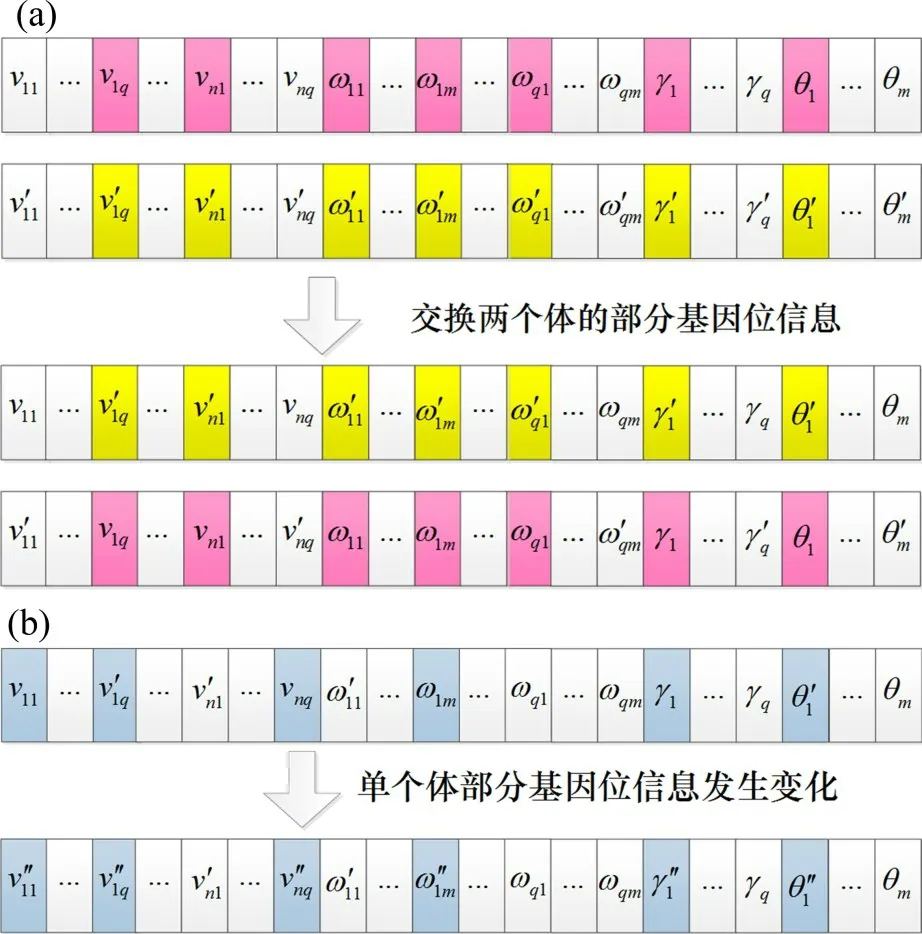
2 实验分析及验证
2.1 拟合效果分析

2.2 预测评估及误差分析

3 结论

