多等级电动出租车充电站选址

吴康利 王立晓

（新疆大学建筑工程学院，新疆 乌鲁木齐 830000）

1 概述

截止2021 年3 月全国汽车保有量达2.8 亿辆，机动车保有量更是高达3.78 亿辆，机动车保有量的增长带来的后果是石油资源、天然气资源的加剧消耗，温室气体的巨量排放，环境气候的不断恶化。在交通运输行业调整能源结构迫在眉睫，发展新能源汽车成为国家解决资源消耗、环境恶化问题的清洁可持续方案。本研究以乌鲁木齐市为案例，探寻电动出租车充电站的最优布局。

近年来，国内外的研究者对充电站选址布局问题进行了大量的研究，其中，由于浮动车轨迹数据（FCD）反映真实世界的出行活动，能提供更为准确的时间空间信息，吸引众多研究者进行深入研究。Cai 等认为出租车在停车时是潜在的充电需求发生点，引入三个标准选择布置充电站[1]。Asamer 等以最大覆盖模型建模，在选址结果基础上利用等时线进一步确定充电站的建站位置[2]。Dong 等通过使用汽车估计数据模拟司机的出行以及充电活动，在此基础上建立预算约束下最小错行次数的优化选址模型[3]。Tu 等利用时空路径工具对出租车需求、电动车出租车与充电站之间的循环交互作用进行了建模，建立电动出租车服务水平和充电站充电服务水平最大化的选址模型[4]。Zhang 等使用成都的出租车GPS 数据建立基于动态分布聚类和重心法的两阶段电动出租车充电站的布局模型[5]。胡培婷等使用广州出租车浮动车数据，建立了基于快速充电的时空需求最大覆盖模型，以覆盖需求最大的充电需求为目标[6]。杨珍珍等提出一种数据驱动的电动汽车充电站选址布局方法[7]。虽然上述研究都利用海量的数据进行充电站选址，拓宽了充电站选址的视野，但是，上述研究鲜有考虑电动汽车司机的偏好因素。

鉴于此，本文基于海量浮动车数据，考虑电动出租车司机的距离偏好，建立最大化满足充电需求与充电站建设成本最小化的多等级充电站充电选址模型。选址模型能给电动出租车充电站选址布局提供参考。

2 模型建立

考虑到现实情况复杂，为了简化模型，作出如下假设：

（1）从浮动车数据中提取出的停车事件作为潜在的充电需求发生点。

（2）按照停车事件发生的时间节点先后顺序安排电动出租车充电。

（3）充电站具有容量限制，且所有充电站内的充电桩总数也存在限制。

（4）出租车司机对前往的充电站的距离存在偏好，仅考虑在容忍访问充电站最大范围内的充电站内进行充电服务。

2.1 参数说明

i 为需求点；

j 为候选站点；

fi为0-1 变量，若需求点i 没有被满足，值为1，否则为0；

Fm为等级为m 的充电站的建设成本；

Xjm为0-1 变量，在候选站点j 建立等级为m 的充电站，值为1，否则为0

Zij为0-1 变量，需求点i 到候选站点j 处进行充电，值为1，否则为0；

Cm等级为m 的充电站内充电桩数；

K 最多可设置充电桩数目。

2.2 数学模型

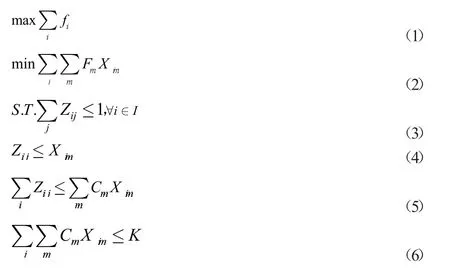
目标函数（1）表示最小化未满足需求点。目标函数（2）表示充电站建设总成本最小化。约束条件（3）充电需求只能在一个充电站进行充电。约束条件（4）建立充电站才能满足充电需求。约束条件（5）充电站具有容量限制。约束条件（6）所有充电站内充电桩数量小于某一值。

3 算例分析

本文以乌鲁木齐市为例，研究范围在东经87.33°-87.77°，北纬43.6°- 44.01°之内。

3.1 研究数据

采用的浮动车数据来源于乌鲁木齐市2017 年6 月5 日0:00 到2017 年6 月6 日23:59 该时段的8011 辆燃气出租车。利用python 对原始数据进行处理，根据车牌ID 提取出租车的出行链，在每条出行链中提取出停车时间在30 分钟到2 小时之间的停车事件。按24 小时分区对停车事件统计，选取停车事件最多的时区作为最终的充电需求。经统计，30 分钟到2 小时之间的停车事件总数为10766 个，其中13 点到14 点时间段停车事件数量最多为885 个。将885 个停车事件赋值容忍访问充电站最大距离，充电站容忍最大距离设定在2 公里到5 公里之间，参考以往研究中对充电站服务半径的设定，概率分布源于马云峰的研究中用户到充电站距离的线性满意度的假定[8]。

充电站等级划分、建设费用以及充电站内充电桩数量如表1 所示。充电桩数量按照国家要求，省会等主要城市公共充电桩与电动汽车比例不低于1:12 的标准设置，本文中充电桩总量为688 台。

表1 充电站的等级划分

使用现有的加油加气站作为候选充电站，不仅能节约社会公共资源，而且司机熟悉度高。选取乌鲁木齐市142 个加油加气站作为候选充电站。

3.2 算例结果及分析

采用NSGA-Ⅱ算法进行模型求解，运用MATLAB 软件编译运行，种群设置为800，迭代次数为400 次，交叉概率0.8，变异概率0.2。迭代曲线如图1 所示，建站费用与未满足需求数两磨边函数在50 次迭代之内就已经收敛。

图1 迭代曲线图

在求解出的多种布局方案中，满足需求数最多布局方案如表2 所示。

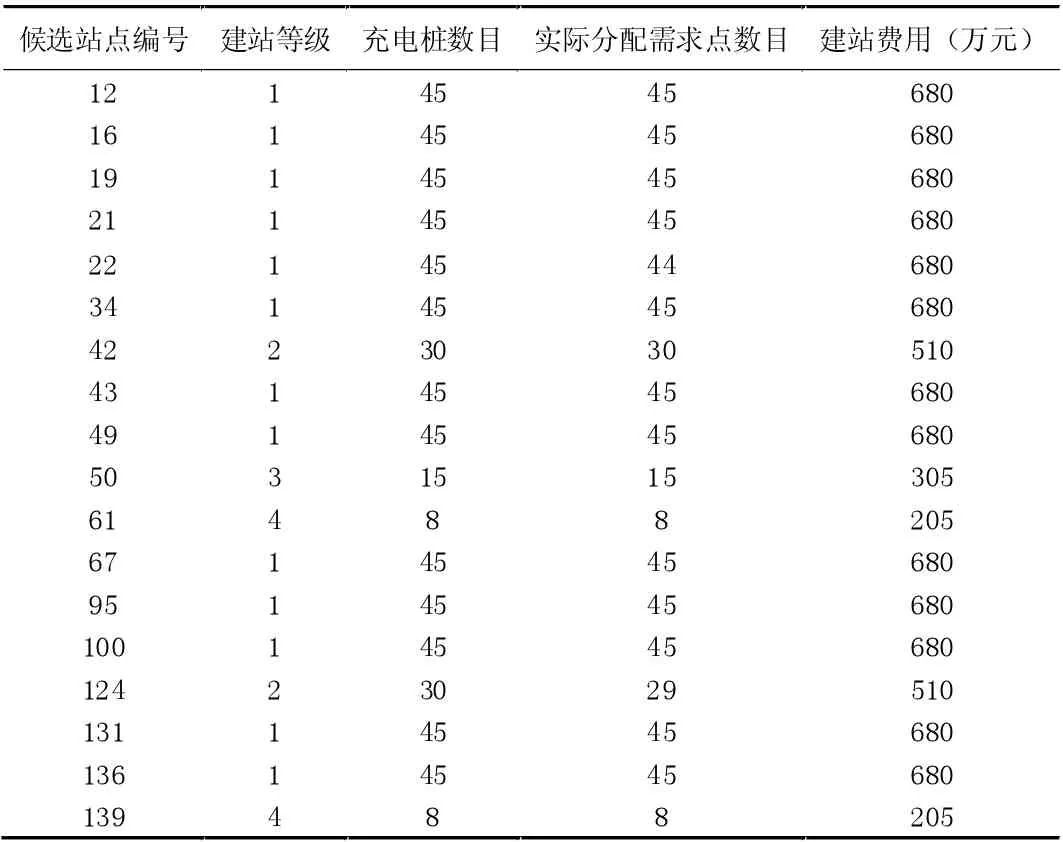
表2 满足需求数最多的布局方案

满足充电需求最多的布局方案中，需建设18 座充电站，其中13 座一级充电站，2 座二级充电站，1 座三级充电站，1 座四级充电站。从各个充电站的需求分配上来看，仅有两台充电桩闲置，利用效率较高。

满足充电需求最多的方案，建设总成本最高，建设总成本最小的方案，满足的充电需求最少。模型求解出其余布局方案，两目标函数处于前两种方案目标函数之间，建设方可依据需求偏好选择布局方案。

4 结论

在考虑用户的距离偏好因素以及出租车的运行特性基础上，建立最大化满足充电需求与充电站建设成本最小化的多等级充电站充电选址模型，考虑到两目标函数不可公度性，采用NSGA-Ⅱ算法求解，多种布局方案可供根据不同偏好选择。