考虑商品组合效应的多任务需求预测模型

黄至言

（华南理工大学电子商务系，广州510006）

0 引言

准确的短期需求预测可以为短生命周期的产品促销、定价、补货和库存计划等决策提供重要的帮助。以服装企业和我国生鲜农产品为例，多数服装品牌商的平均产销率仅为50%~65%[1]，而生鲜农产品2019年损耗率也高达25%~30%1数据来源：https://www.sohu.com/a/342685335_757817。这意味着由于缺乏准确的短期需求预测，市场中大量的缺货和积压并存。另外，库存周转速度的加快，也让企业的补货间隔不断缩短。以京东商城为例，2020年第三季度京东的库存周转天数已低至34天2数据来源：https://www.163.com/dy/article/FRKKM3KD0512AE4K.html。以年月为单位的需求预测已不能完全满足企业的需求。可以看出，准确的短期需求预测能为企业快速响应市场变化提供重要信息参考，是企业管理的重要任务之一[2]，也是企业打造敏捷供应链的关键。因此，提高短期需求预测的准确度具有极强的现实意义。

现有文献一般称对未来较短时间内（本文以未来一天为例）商品被购买量的预测为短期需求预测[3]。具体的，假定系统中商品集为R，共有N条销售记录，1≤n≤N。本文使用集合Dn={rn1,rn2,…,rnzn}⊂R代表第n条记录（zn代表第n条销售记录中的商品序号），Dn同时表示一位顾客在一次消费中分别购买了rn1,rn2,…,rnzn等商品（这里为了简化问题，我们假设每件商品各购买一件）。我们希望基于D1~DN预测商品i第L+1天的日需求量{X̂i,L+1}，其中L为已知销售数据的最后日序号。为进行短期需求预测，目前主流的策略是通过多个样本进行模型拟合。常见的模型包括指数回归模型[4-7]，整合移动平均自回归模型（auto regressive integrated moving average model，ARIMA）[8-10]和支持向量回归模型（support vector regression，SVR）[11-12]等。这些模型通过品项以往的历史数据对自身的参数进行训练，并选择在历史数据中表现最好的参数作为预测模型的参数。然而，近年随着线上交易技术和制造技术的发展，短期需求逐渐呈现不确定性大，可供训练的数据不足等难点。这是因为商品的影响因素从线下拓展到了线上，以及商品的迭代的不断加快。以两个著名的公开销售数据集（E-Com⁃merce3数据来源：https://www.kaggle.com/carrie1/ecommerce-data和SuperStore4数据来源：https://www.kaggle.com/jr2ngb/SuperStore-data，具体介绍见下文第2.1小节，下文简称EC数据和SS数据）为例，我们可以发现日需求曲线极不平滑（如图1所示），仅靠商品自身的历史销售数据难以得到一个有效的预测模型。

图1 E-Commerce数据和SuperStore数据所有商品的日需求

为了解决自身训练样本不足以有效训练模型的问题，近年学者们提出了多任务学习（Multi-Task Learning，MTL）[13]模型。MTL中的“任务”一般指通过训练样本拟合模型参数。而本文主要关注的是回归模型参数的拟合。MTL主要动机是把其他相似任务的训练样本纳入自身模型的拟合，从而解决自身训练样本不足的问题。现有的做法包括使用L1正则化和L2正则化的Group LASSO模型[14]和使用Wasserstein距离作为正则化的MTW模型[15]。Ma Shaohui在面对大品项背景的需求预测任务时，使用带有L1正则化的回归模型很好地利用了品牌促销政策的相互作用提高预测准确度[16]。Gong Pinghua等把任务间的权重系数分解成两个矩阵并分别用L1和L2正则化进行约束[17]。以上工作通过不同任务的相似性约束鼓励不同模型选择相似的少部分样本特征而忽略样本的其他特征。然而，通过正则化项为多个任务选择相似的重要特征并不适合商品的短期需求预测问题。在本文问题背景中，一个商品的预测模型的训练被视为一个学习任务，每个学习任务的预测都需要通过历史销售数据进行拟合。

我们注意到虽然短期内需求量的变化具有很大不确定性，但商品的组合关系却比较稳定。直观上，若商品A和商品B共现频率高且商品A或商品B的出现意味另一商品很可能出现，那么商品A和商品B很可能具有相似的需求趋势。为方便描述，本文称这种现象为商品组合效应。简单来说，如果两个商品在各个订单中出现的概率相似，则商品A和商品B存在商品组合效应。以EC数据为例，本文分别通过季节性因素和商品功能特点人工找到的两组商品组合，它们是（a）季节性明显的冬季商品和（b）功能特点比较明显的派对商品，如图2所示。我们发现与冬季商品组合中在冬季有着明显的上升趋势而在夏季有明显下降趋势。而派对商品在英国重要的节日也均有上升趋势而在非节庆日有下降趋势。

图2组合商品的需求趋势相似性

基于上述发现，本文希望通过为每个商品选择与其有相似趋势的商品，并在多任务学习框架中共享训练样本，进而提高短期需求预测的准确度。为解决上述问题，本文构建了一个考虑商品组合效应的需求预测模型（Multi-Task Linear Regression，MT-LR）。本文首先使用非参数贝叶斯模型把商品组合信息嵌入到商品特征表示中，令在该特征空间中接近的商品更可能在订单中共现。然后本文对线性回归模型进行改进得到一个新的多任务需求预测模型。在模型求解上，本文首先参考了隐狄利克雷模型（Latent Dirichlet Allocation，LDA）的求解方法，对商品特征进行了学习，然后使用梯度下降的方法优化回归模型参数。本文将提出的模型应用于英国某线上礼品店和某全球连锁超市的商品需求预测中，结果显示，与主流模型相比，本文所提的MT-LR具有更低的误差。

1 多任务学习线性回归模型（MT-LR）构建

本节将介绍通过LDA把商品的组合关系嵌入到商品特征表示中的做法，以及根据该商品特征表示提出的考虑商品组合效应的多任务学习模型MT-LR。

1.1 基于LDA的特征嵌入模型

LDA[18]是当前最有影响的文本主题挖掘模型之一。LDA已被很多工作证明了其在隐藏信息挖掘方面的能力[19-20]。应用LDA作为商品关系的特征嵌入模型主要是因为客户往往由一些隐藏的动机（LDA中的主题）推动其购买决策。每一个购买动机又由客户偏好的商品组成。例如客户需要购买食物，食物又由“猪肉”、“牛肉”和“面条”等商品组成。根据LDA的假设，同一购买动机的代表性商品更容易在同一订单中共现。因此，本节我们提出基于LDA的商品特征表示方法。该方法把LDA的变分分布参数转化为商品的特征表示，并采用JS散度衡量商品间的相似性，成功把商品组合信息嵌入到商品特征空间中。

LDA可以生成若干（主题数由用户指定，记为K）的“主题”，其中每一主题都由若干词汇共同刻画。且LDA为了描述不同文档的混合主题分布，使用N个概率向量θi,i=1,…,N描述，其中θi共有K维，N为文档数。在本文情景中，我们使用与LDA完全相同的方式表示销售记录：即把卖场的每个商品品类视为一个词汇，记作r,r=1,…,R，每个交易对应的商品明细视为一篇文档，记作Di，且把购买的动机视为文档中的主题。根据LDA的表示，隐藏的动机可视作为商品的分布，记作概率向量φk,k=1,2,…,K，当给定购买动机k时，购买商品r的可能性就为φk,r。记ΦK×|R|为把K个向量放在一起所组成的矩阵，|R|为商品集规模。φk服从以参数为βk的狄利克雷（Dirichlet）分布，符号表示为：φk~Dirichlet(βk)。另外，根据LDA的生成过程，一个订单中可能由多个隐藏的动机构成，如“食物”和“饮料”。记订单i的一个商品是由动机k驱动的可能性为θi,k，符号表示为θi~Dirichlet(α)。其中α是一个描述客户普遍动机分布的K维的向量。可以看出，当我们记Zi,n∈{1 ,…,K} 为订单i中第n个商品yi,n的实际购买动机时，那么订单i包含商品m的概率为：

因为具有商品组合效应的两个商品在所有订单中的出现概率应尽量接近，所以如果商品r和商品r'具有商品组合效应，他们应该满足下式：

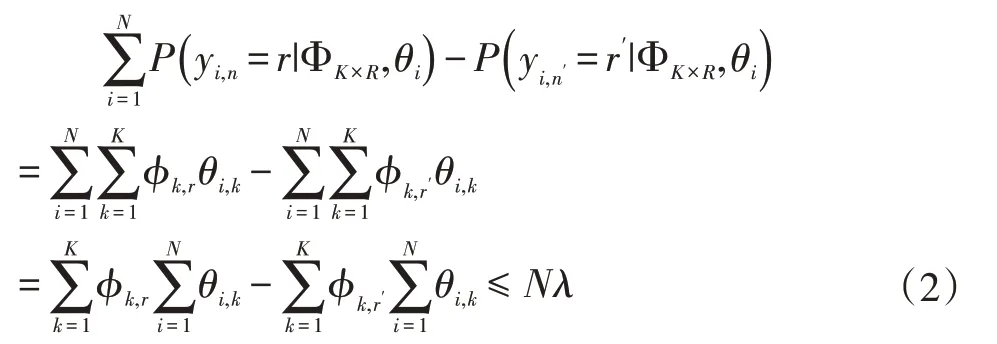
其中λ为商品组合效应阈值，值越小意味着组合效应越强。高于阈值时，我们把商品r和商品r'视作无商品组合效应。根据LDA的文本生成过程，订单i由动机k驱动的期望为：

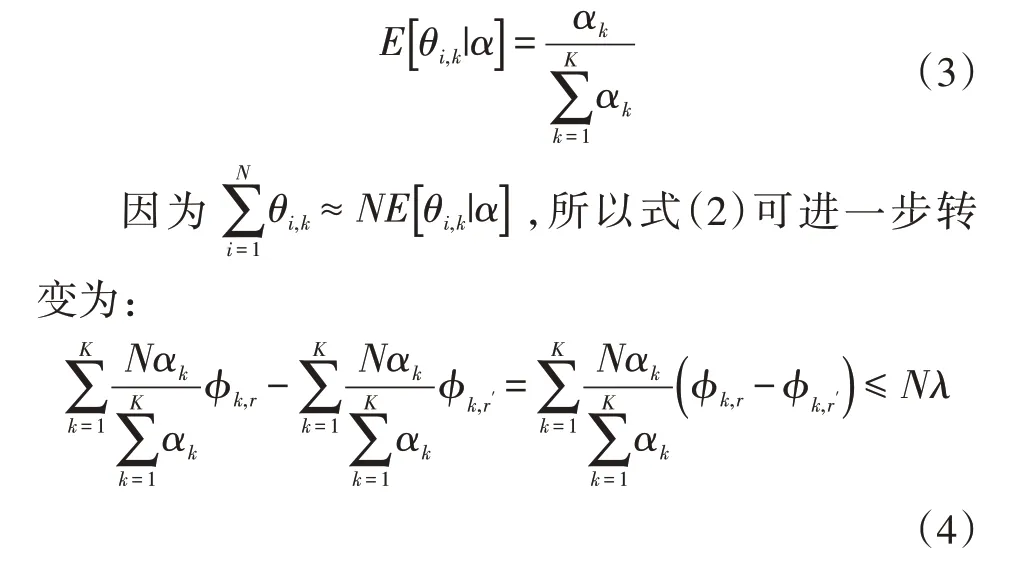
这意味着如果商品r和商品r'具有商品组合效应，那么它们应该满足：

Blei等提出了一种变分推断模型用于LDA问题的求解[18]，由于本文的数据产生模型与文献[18]中文档生成模型完全一致，所以我们可以把文献[18]中的求解模型应用于本文，从而获得分布参数β1,…,βK，进而获得商品r的向量化表示

下面我们考虑如何根据商品r的向量化表示度量商品的组合关系。我们已知如果商品r和商品r'具有商品组合效应，他们应满足式（5），且商品的向量化表示本质上是商品在各动机下的分布。因此，为了度量商品之间的关系，我们使用JS散度度量商品之间的相关性。JS散度衡量的是两个概率分布之间的距离，如果商品r和商品r'在各个主题下出现概率接近则JS散度小，反之则大。记商品相关性矩阵为ρR×R，商品r和商品r'的向量化表示分别为p和q，它们的相关性为ρr,r'，那么：

ρr,r'越小表示商品r和商品r'商品组合效应越强，需求趋势越可能相似。

1.2 需求预测模型构建与求解

直观上，相关性高的商品拥有着相似的需求趋势，这意味着在短期需求预测问题中我们可以利用该信息更稳定地进行预测。具体来说，商品组合效应高于相关性阈值的两个商品短期内有着稳定的需求量比例，即基于自身训练样本求得的预测值能以一定比例转化成其他品项的同期需求量。

本文考虑给定多个品项的长度为L的时序销售数据{Xr,1,X r,2,…,X r,L},r=1,…,R，以及根据这些数据生成的相关性矩阵ρR×R（R为全部商品集合），预测商品i第L+1天的日需求量。本节提出多任务学习线性回归模型MT-LR以及优化目标函数式。MT-LR模型为：

根据商品组合效应，各商品的预测（每个商品的预测视为单独一个任务）应往相似性较大的商品按比例偏移。因此，目标函数F设计为：

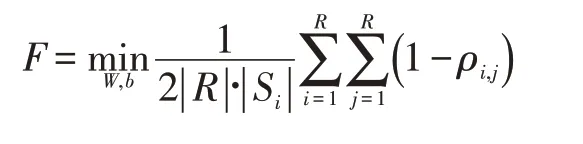
2 实验

本文把所提算法应用于两个真实的销售数据集上并与基准算法进行比较。

2.1 实验数据介绍

我们把所提出的模型应用于Kaggle上的EC数据集和SS数据集。EC数据集包含了一家在英国注册的线上零售商从2009年12月1日到2011年12月9日内的41393张销售订单数据，涉及4802个不同的品类（SKU）。该零售商主营的商品包括有烘烤（糕点）工具、家居派对饰品、手工制作工具和礼物包装工具等。其中有超过90%的销售订单包含了两个以上的商品，蕴含了丰富的商品组合信息。而SS数据集是一家全球线下连锁工业超市的销售数据，包含2011年1月13日到2014年9月9日的共21559张订单，涉及9751个品项，主要包括办公用品和工业生产用品，如粘合剂、信封、纸、印刷机和电话。Super⁃Store数据只有42%的销售订单包含两个及两个以上的商品。因为线上和线下两种销售方式将表现出较多不同数据特质，且组合行为发生的频率也要差别，所以基于这两个数据进行实验可以有效说明模型在不同业务背景下的性能。

2.2 评价指标

下文实验使用两个评价指标定量地评估模型性能，分别是均方根误差（Root Mean Square Error，RMSE）及平均绝对误差（Mean Absolute Error，MAE）。其中RMSE对偏差较大的样本较为敏感，容易受部分偏离程度较大的样本影响；而MAE衡量预测值与实际值之间的绝对误差，不容易受预测值与实际值误差较大的样本影响。RMSE和MAE的具体计算公式如下：

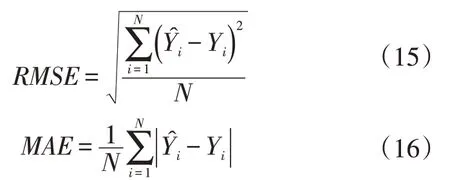
其中N是样本规模，̂是第i个样本的预测值，Yi是第i个样本的真实值。

2.3 预测性能比较

提高短期需求预测准确度是本文的主要任务。本节将以单任务框架下的线性回归模型（LR）、支持向量回归模型（SVR）[12]、简单指数平滑模型（SES）[4]、holt-winter指数回归模型（HW）[7]、整合移动平均自回归模型（ARIMA）[8]以及基于L1正则化的Group LAS⁃SO模型[16]作为对比算法，对比它们与本文所提的MT-LR在EC数据集和SS数据集中的RMSE和MAE对比来观察MT-LR的预测性能。

在基准算法中，LR、SVR、SES、HW和ARIMA属于单任务学习模型，Group LASSO属于多任务学习模型，其中LR作为MT-LR的基础主要观察考虑商品组合效应后的多任务学习的比原模型的提升幅度，而SVR因其鲁棒性较强，适合短期需求预测问题，也可作为基准算法。在SVR核函数选择中，本文选用了常用的高斯核。SES和HW同属指数回归模型，SES是HW的基础，HW是专门针对带有短周期趋势的问题所提出的指数回归变体。ARIMA是经典的时间序列预测模型，而Group LASSO是经典的MTL实现方法，是很好的对比算法。

本文通过分别在EC数据集和SS数据集中随机挑选连续两个月3000个商品的历史销售记录（EC数据在2010年2月2日~2011年12月9日随机选择连续的两个月，SS数据在2011年4月14日~2014年9月9日间随机挑选连续的两个月），以1:1的方式划分成训练集和测试集，然后观察各模型经过训练集训练后在测试集中的测试误差RMSE和MAE。以上过程独立重复30次得到实验结果。实验中，我们设学习率η=0.01，收敛精度tol=0.01，商品组合效应阈值设为λ=0.1，最大迭代次数为500。具体实验结果如图3—图6所示。为展示多次短期需求预测实验的效果，以下实验均使用箱型图。在箱型图中，框体以外的黑色小点为异常值，框体及上下突起的横线从上到下分别是最大值、上四分位数、中位数、下四分位数和最小值。其中各模型在EC和SS数据集中的平均RMSE和平均MAE如表1所示。

表1平均RMSE和平均MAE汇总

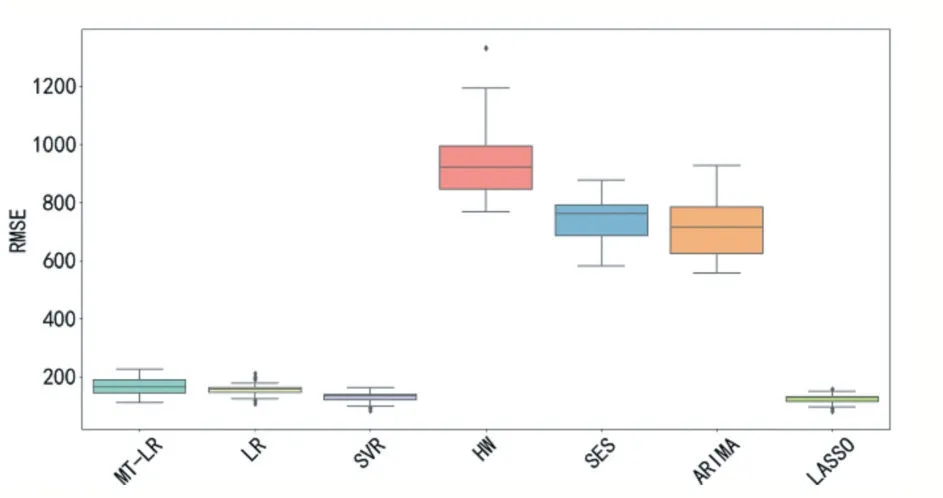
图3 EC数据中各模型RMSE比较

图4 EC数据中各模型MAE比较

图5 SS数据中各模型RMSE比较

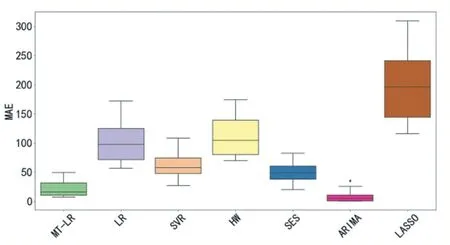
图6 SS数据中各模型MAE比较

图3—图6及表1中，RMSE或MAE的值越小，代表预测精度越高。MT-LR位于4幅图中的最左一列。表1加粗字体代表表现较好的模型。可以看出，在预测误差方面，本文所提的MT-LR模型在两个数据集中均接近或低于其他6个基准方法，特别是在SS数据中明显好于除ARIMA外的其他5中基准方法。并且对比其他基准算法可以发现，其他算法在RMSE和MAE的对比上差异较大，这说明MT-LR比起其他模型预测的稳定性较高，不容易出现预测误差较大的样本。这体现了MT-LR在短期需求预测问题中明显的优越性。

MT-LR共享训练样本的关键在于相关性矩阵。我们需要确定模型中的相关性矩阵对于预测误差减少的作用。我们设计如下实验：

本文通过随机生成相关性矩阵与基于LDA进行特征嵌入后的JS散度度量的相关性矩阵进行比较，每次在EC数据集和SS数据中随机挑选连续的两个月并按1:1的比例划分训练集和测试集，独立重复30次上述实验，观察随机生成的相关性矩阵能否达到与我们相同的结果。我们设学习率η=0.01，收敛精度tol=0.01，最大迭代次数为500，实验结果如图7所示。

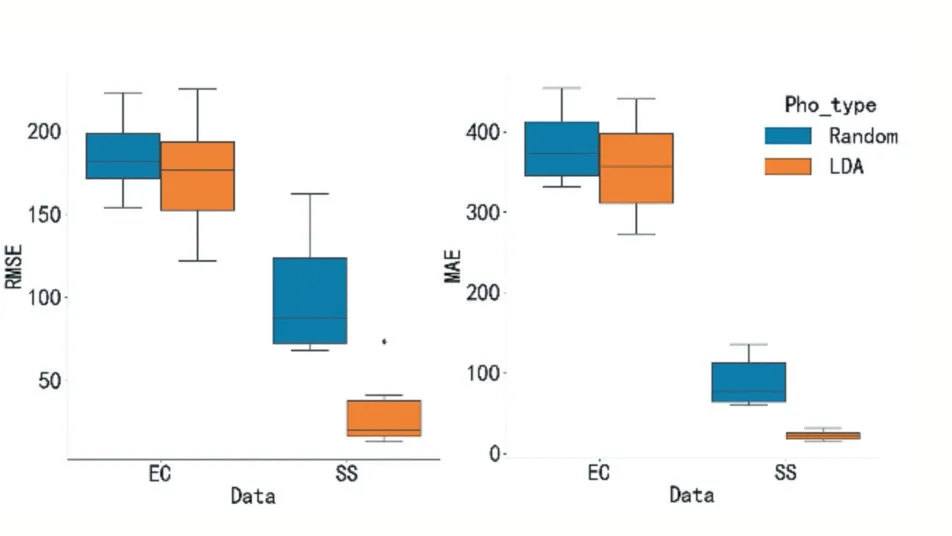
图7随机生成相关性矩阵与基于商品组合效应的相关性矩阵性能比较

图7中，蓝色代表随机生成的相关性矩阵在EC和SS数据集中的RMSE或MAE误差，橙色代表由LDA特征嵌入后并使用JS散度度量相关性的相关性矩阵在EC和SS数据集中的RMSE或MAE误差。从图中可以看出随机生成的相关性矩阵的RMSE和MAE比基于LDA进行特征嵌入后并使用JS散度度量相关性的相关性矩阵高，也就是说当我们在MTLR和MT-ESVR的原有基础上把相关性矩阵替换为随机生成时，增大了模型误差。因此，从预测误差的指标来看，使用LDA进行特征嵌入并使用JS散度度量相关性可以提高模型的预测性能，有效降低商品预测误差。

3 结语

本文针对短期需求预测问题展开研究，考虑了商品组合效应，建立了一个基于线性回归的多任务学习需求预测模型。本文所提的MT-LR模型使用LDA把商品的组合信息嵌入到每个商品的向量化表示中，然后通过JS散度度量商品的相关性，最后基于所得到的相关性矩阵共享各个品项的销售数据。基于真实数据的实验表明，MT-LR有效提高短期需求预测的准确度和稳定性，克服了训练样本不足，数据不确定性大等难点，为企业快速响应市场需求提供了重要的信息参考。

多任务学习需求预测模型中，比较关键的是相关性矩阵的计算以及商品组合信息的应用，如何更高效地确定及利用商品组合关系是下一阶段研究的重点。同时，把商品组合信息结合到非线性等其他拟合能力更强的模型（如支持向量回归模型）也是提高需求预测模型性能的一个可行研究方向。