基于BP网络的字符识别算法

王汝心，马维华

（南京航空航天大学计算机科学与技术学院，南京210016）

0 引言

字符识别应用于多个领域。常用的字符识别方法包括基于模板匹配[1-2]、基于特征分析匹配[3]和基于机器学习[4-6]。字符特征有网格像素统计、正交投影法、骨架特征等方法，但这些特征提取方法各有侧重，具有局限性，当字符相似时识别效果较差。随着机器学习算法的研究进展，机器学习算法被越来越多的应用到字符识别领域。孙国栋、江亚杰等使用训练好的BP（Back Propagation，反向传播）网络对图像全局阈值进行预测并二值化，达到分离重影的目的，并采用改进LeNet-5网络完成字符识别[4]。呙润华、苏婷婷等通过总体密度、分块密度等特征表达不同字符的差别，以减少后续工作的计算量，将模板匹配方法嵌入到收敛的BP神经网络中，在提高系统的计算效率、缩短运行时间的同时提高了字符识别效率[6]。

本文将骨架提取与BP网络相结合，在细化图片、保留原字符特征的同时引入字符图片中更多的特征，优化BP网络，以提高对尺寸偏小的图片的识别准确度和精确度。

1 特征提取

1.1 骨架提取

骨架提取（image skeletonization）是实现二值图像细化（image thinning）的运算方法之一。当图像本身尺寸偏小、或者当字符图案在图片整体中所占区域过小时，进行字符分割后获得的字符图片往往像素点偏少，导致提取特征时能够提取的特征向量个数也会随之减少，因而会对字符识别结果造成影响。对图片中的字符笔画进行细化，提取字符的骨架，从而在不改变字符的轮廓特征的同时，突出字符与字符之间的细微区别

对一个二值图像而言，骨架可以理解为图像的中轴，它是一种细化结构，描述了目标的拓扑结构。细化过程就是将图像中的像素点剥离，图像有规律地缩小，在保持原图案形状的基础上，逐步删除原图像中的部分像素点，直到获得图像的骨架。

保证图案形状不变，应保证图像的连通性质不变，减少线条相交处的畸变，在细化过程中，应判断一个点p1是否能去掉时，应参考该点的相邻8个点的情况。在这9个点中，只有当p1不是内部点、且不是端点、且不是固定点、且是边界点、且去掉p1后，如果连通分量不增加时才可删除p1点。

如图1所示，当p1周围的8个点满足图1（b）、（c）、（d）中任意一种情况时，p1点都不能删除。

根据以上条件可以推导出，对于图像中的任意像素点p1，只有同时满足以下4个条件时才能将p1点删除：

（1）f(p)=p2+p3+p4+p5+p6+p7+p8+p9，则f(p)应满足2≤f(p)≤6。

结合图1可知，当p1为孤立点时，f(p)的值为0；当p1为端点时，f(p)的值为1；当p1为内部点时，f(p)的值为7或8。由此得出，当2≤f(p)≤6时，排除了p1点是端点、孤立点或内部点的可能性。

（2）在序列{p2,p3,p3,p4,p4,p5,p5,p6,p6,p7,p7,p8,p8,p9,p9,p2}中，0,1的数量为1，以保证图片的连通性不发生改变。

（3）p2*p4*p8=0或者A(p2)≠0，其中A(p2)表示p2周围8邻域的0,1的数量，以保证2个像素宽的垂直区域不完全被腐蚀掉。

（4）为了保证2个像素宽的水平区域不完全被腐蚀掉，应满足条件p2*p4*p6=0或者A(p4)≠0，其中A(p4)表示p4周围8邻域的0,1的数量。

图1细化条件

1.2 HOG提取

为了减少计算复杂度、时间消耗和空间消耗，对分割好的字符图片进行分析，从大量数据中提取中关键信息转换为若干特征。本文通过提取字符的HOG特征，在描述目标特征的同时获取分布向量。

提取HOG特征共分5步：

（1）分割图像为2×2像素的连通区域；

（2）采集连通区域内的像素点，通过垂直梯度算子[- 1,0,1]T，水平梯度算子[- 1,0,1]提取像素点的水平和垂直梯度。

（3）计算水平和垂直方向的合梯度，包括幅值和方向。

（4）以2×2个连通区域为一个block，将block中的HOG向量拼接并归一化。

（5）滑动步长设定为1个像素，计算图像整体的HOG特征向量。

2 BP分类器

2.1 BP网络构建

BP神经网络分为两个过程：将输入信息正向传递，完成一次训练过程；将实际结果和预测结果的误差反向传播，修正各层的权重。Robert Hecht-Nielsen曾提出万能逼近定理，证明了包含一个隐藏层的BP网络可以用于拟合任意闭区间内的连续函数。换言之，假设单个样本具有m个样本特征、n个输出向量，一个包含输入层（I）、隐含层（H）、输出层（O）的三层的BP网络就可以完成任意的维到维的映射。当m=3、n=3时，BP网络如图2所示。

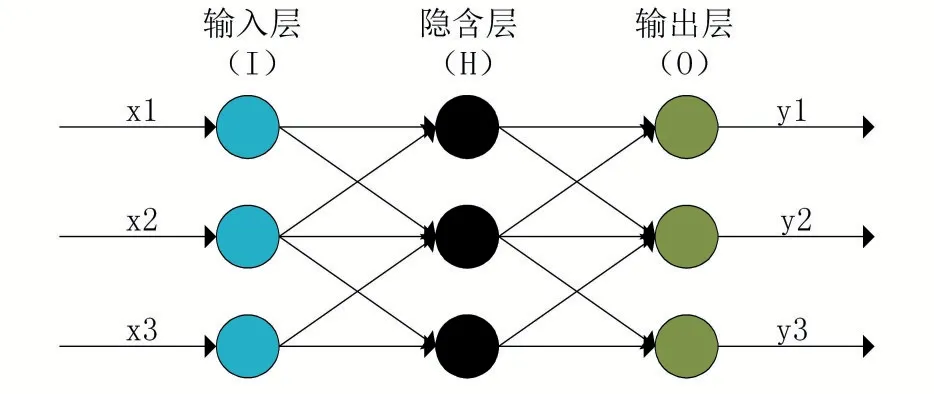
图2 BP网络

假设有a个训练样本，那么对于第p个输入，输入向量为Ip=(ip1,…,ipm)T，目标输出向量Tp=(tp1,…,tpm)T，最终输出向量表示为Op=(op1,…,opm)T。以wij表示输入向量第j（j=1,2,…,m）个分量到输出向量的第i（i=1,2,…,n）个分量的权重。则第p个输入下输出方差为：

其中，p=1,2,…,a。则网络总误差如公式（2）所表示：

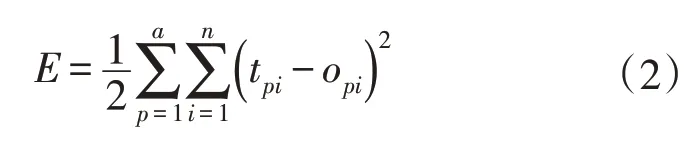
根据梯度下降法和Widrow-Hoff规则，连续调整网络的权值和阈值，wij应沿着相对误差平方和方向，权值矢量的修正值和当前位置上的E的梯度成正比，则对于第j个输出节点，有：

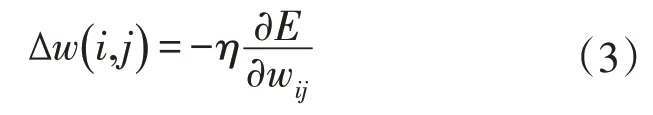
重复上述过程，以修正各层神经元之间的连接权重，使得期望输出值在误差阈值的允许范围内。

2.2 BP网络优化

由于BP网络中的极小值较多，易于陷入局部极小值，而无法获得全局最优值。所以通过以下方法优化BP网络。

（1）多次随机训练，选择使训练后效果最好的初始值。在依据误差函数进行BP网络训练以得到最小误差的过程中，需要以初始值为基础和起点，所以初始值决定了BP网络的收敛方向。并采用退火思想允许E按照一定概率上升，从而减少BP网络陷入局部最小值的可能性。

（2）增加动量项∝。通过增加动量项，增大搜索步长，从而加速算法收敛，同时可以降低BP网络对误差曲面局部区域的敏感性。根据BP网络的思想，第n-1次的迭代结果影响力第n次迭代中，神经元之间的权值更新，所以在迭代过程中采用公式（4），其中动量因子∝一般选择0.1~0.8。

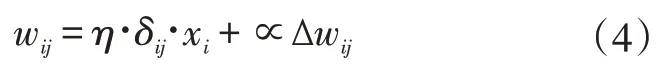
（3）自适应调节学习率。学习率的大小影响了BP网络的收敛快慢和训练成果。当学习率取值较小时，训练更容易稳定收敛，但取值过小会导致BP网络训练时间变成、运行速度降低等问题；当学习率取值较大时，可以加速收敛，训练结果可能震荡发散。因此，为了选择合适的学习率，应采用自适应方法调节取值大小。

（4）通过优化隐含层数和隐含节点数目完成网络结构优化。若隐含节点过少，可能导致精度降低；若隐含节点过多，虽然能提高精度，但由于网络结构过大导致BP网络性能下降。艳霞、李禹生等曾就隐藏节点数目与BP网络性能之间的关系进行实验，结果表明，当隐藏节点数目为取20~40时BP网络性能更好[7]。

3 性能评估

隐藏层选择Sigmoid型函数作为变换函数，隐藏层节点设置为30个，采用自适应学习算法，目标误差设置为0.001，或执行30次迭代训练。将样本数据集进行骨架提取，所得结果图片作为BP网络的训练数据集。获得迭代次数和识别正确率的数据后，将隐藏层节点设置为40个和50个。在图3中，展示了迭代次数、识别正确率、节点个数三者之间的关系。

从图3可以看出，第一次学习迭代的识别正确率普遍较低，在第10次迭代之前，正确率的波动较大。在第10次迭代之后，正确率趋于稳定。在多次迭代、正确率稳定后，当隐藏层节点设置为30个时，平均正确率为93.88%，最大正确率为94.36%；隐藏层节点设置为40个时，平均正确率为94.23%，最大正确率为95.06%；隐藏层节点设置为50个时，平均正确率为95.20%，最大正确率为95.60%。

综合考虑迭代次数的多少、隐藏层节点数目和网络结构复杂度等因素对训练结果、训练时间的长短的影响，设置隐藏层的神经元个数为50个，令BP网络迭代训练30次。

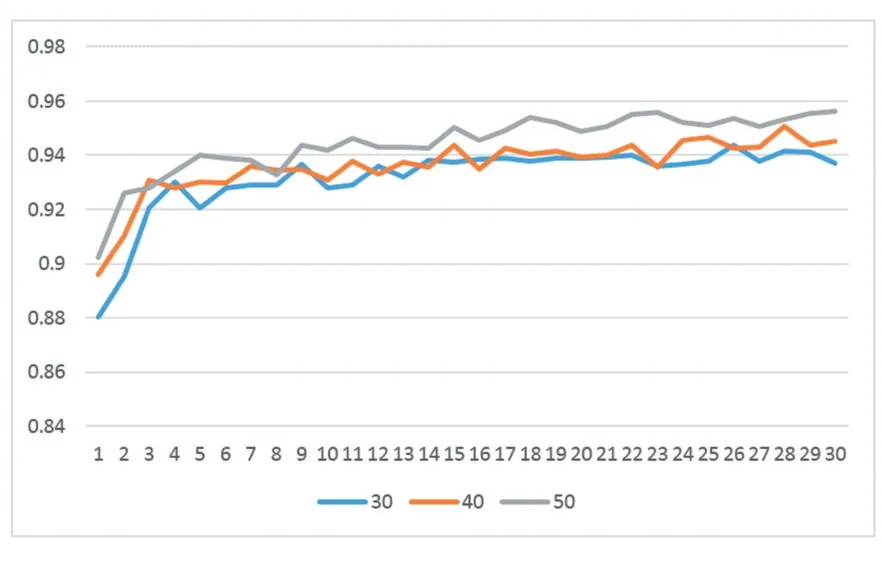
图3迭代次数与正确率之间的关系

将测试样本数据集进行骨架提取，将所得结果图片作为BP网络的输入，得到字符识别结果，并对识别结果进行统计，以测验BP网络对低像素图片的识别效果，得到BP神经网络对骨架提取后的字符图片进行识别，正确率为95.55%。将识别错误的图片经过图像细化、HOG特征提取后，通过BP网络进行识别，正确率为95.65%。

4 结语

本文通过分析低像素图片的特征，将二值图片的骨架提取与BP神经网络相结合。通过骨架提取细化图片中的字符图案，判断像素点是否应删除的依据，并进行HOG特征提取。构建BP网络，并对BP网络进行优化，完成对低像素图片识别算法。对BP网络进行训练，对隐藏层节点个数、迭代次数和识别正确率进行统计和分析，迭代次数为30次，隐藏层节点个数为50个。将测试样本数据进行图片细化，通过BP网络进行识别，正确率为95.55%。