从内部逻辑中找准“生长点”构建课堂的思考

徐小青

[摘 要]数学教学，如何寻找“逻辑关联点”，是教师智慧的体现.可以从生活经验入手，赋予数学实际背景，也可以不走“寻常路”，回归数学本质，从数学内部逻辑关系中找准“生长点”构建课堂，让课堂绽放光彩.

[关键词]数学;逻辑;生长点;构建课堂

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2021）29-0008-02

建构主义学习观认为，学生的学习本质上是一种“认知建构”的过程.新知识只有在其成为个体认知建构的一个组成部分时，才算是意义建构的真正完成.笔者认为，教师应该从知识结构中厘清先后关系，然后在学生当前的认知结构中寻找“逻辑关联点”（“生长点”）作为新知建构起点.因为关联点往往不止一个，各个关联点与新知之间的可类比程度、抽象程度也不相同，所以建构起点的选择成为教师智慧的主要体现.下面笔者就以几个教学片段为例，谈几点思考.

一、回归根本，建立生长点

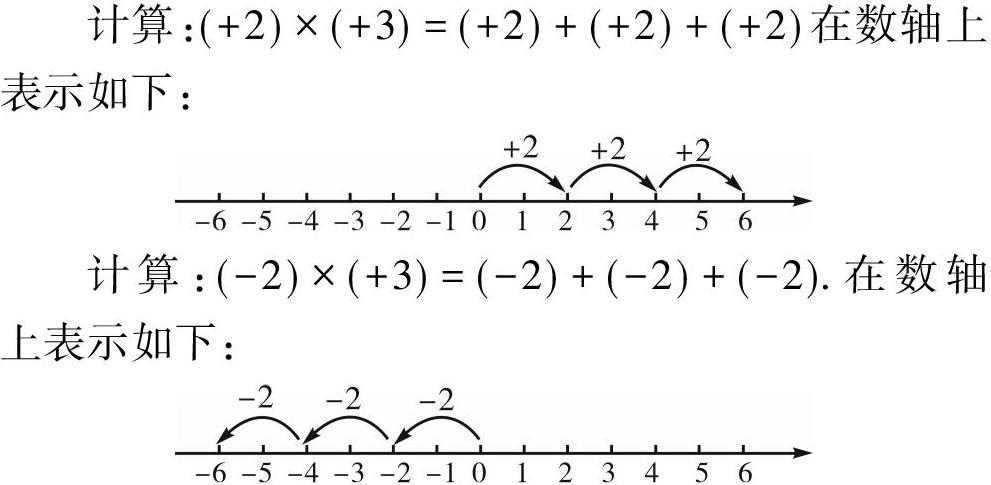
运算教学中，“法则由来”是教学的核心，它能够帮助学生理解算理，掌握算法.基于初中生的学习要求，有理数的乘法法则是根据现实问题和规律探索归纳得到的，有理数的除法是作为乘法的逆运算得到的.学生在小学时已学习了非负数的乘法，也在初中学习了数轴可以表示有理数加法计算，还有一定的生活经验运用到了乘法（主要是非负数之间的乘法），这三部分都与乘法法则的推导有一定的逻辑关联.如何选取才能让学生体会到含负数乘法的合理性.

教学片段1：

问题提出：类比有理数加法的运算，你认为有理数的乘法运算有哪些类型？运算结果又怎样？

学生新接触的运算教学，情境的引入也可以是多种角度的.如何选取恰当的情境，帮助学生更好地理解算理，掌握算法，需要我们找到合适的生长点.开方运算是一种新型运算，学生对其没有经验可言.那么平方根的生长点又在哪里呢？笔者从运算之间进行了寻找.

教学片段2：

活动一：

问题1：已知一个正方形的边长8 cm，这个正方形的面积是多少？

这个问题实际上是求82=（）.

问题2：已知一个正方形的面积为81 cm2，这个正方形的边长是多少？

这个问题实际上是求（）2=81.

比较上述两个问题中的运算的区别和联系.

出示平方根的定义.

赏析：教材中采用的是在方格纸中已知直角三角形两直角边求斜边有多长的问题引入.学生可以从中体会研究平方根的必要性.但也有弊端，这一运算和学生已有认知中的哪类运算关系最紧密，体现不明显.此教学片段中，从两个问题的计算引入.问题1中的运算实际上是乘方运算中的平方运算，已知底数求幂的过程.问题2中的运算是谁的平方等于81的问题，已知幂求底数的问题.比较中不难发现两者之间实际是一个互逆的过程，也就是平方运算和开平方运算是一种互逆运算，平方根的定义就呼之欲出.

二、从学生经验找准“生长点”

在苏科版教材中，《有理数的乘方》这节课是新接触的概念课.学生在此之前学习过有理数的乘法，也有生活中折纸后纸的层数、拉面根数的生活经验，还有数青蛙的儿歌.这三方面内容都与乘方有一定的逻辑关联，都可以作为本节课的引入，但哪一些更接近学生当前主观认知结构，就是教师需要寻找的一个节点.

教学片段3：

活动一：

问题1：边长为3 cm的正方形的面积怎么表示？

问题2：棱长为5 cm的正方体的体积怎么表示？

问题3：将一张报纸对折再对折……对折两次，报纸的层数怎么表示？对折三次呢？对折四次呢？

问题4：你还能举出类似的实例吗？

一个细胞30分钟后分裂成2个，经过5个小时，一个这种细胞能分裂成多少个？（如图1）

赏析：教学过程中，教师放弃了生活情境，选择从学生经验入手.先是用小学时已十分熟悉的计算正方形的面积、体积引入，这是学生最初接触的乘方，也深知算式的特点.报纸问题也是生活中常见的实例，学生对对折后它的层数研究并不多，直接列式会让一部分学生无从下手.有了上一问的铺垫，学生对生活中折报纸后层数问题有了一个类比的对象，不难列出算式.解决了一个生活中的问题，也进一步了解这类运算的特点.接着问“你还能举出类似的实例吗？”既要求学生收集生活中的数学中的例子，丰富对这类运算的认识，也有助于学生内化这一运算的特点.教师并没有就此引出定义，而是又给了一个学生较陌生的细胞分裂问题，让学生对相同因数的个数有一个主动思考的过程，再次剖析了这类运算的特点.整个过程经历了由“熟悉—半生半熟—陌生的”三个部分内容，建立了不同的台阶，多层次体会相同的因数，因数的个数以及它们之间的关系，乘方的定义呼之欲出，此时再下定义就水到渠成了.

三、搭建桥梁，连接生长点

《科学记数法》是学了乘方运算后的一节衍生课，学生已经有了乘方的经验，会表示整百整千数的幂的形式，为科学记数法奠定了一个必要的知识基础.而后立刻引入科学记数法的表示，将已经掌握的幂的知识迁移到科学记数法中.看似水到渠成，在实际课堂中学生却状况频发，不知方向.该如何在学生“已经掌握的知识”和“需要掌握的知识”之间架起一座桥梁？教师在探究完整十整百数的幂的形式后，对教学过程做了如下调整.

教学片段4：

把下列數表示成一个数与10的乘方的积的形式.

（1）300 000 000

=3×100 000 000

=3×108

（2）25 000 000 000 000

=25×1 000 000 000 000

=25×1012

（3）265 900

=2 659×100

=2 659×102

思考：观察上述几道算式的运算过程，你有什么体会？是不是都将较大数简单地表示出来了？

赏析：联系已学知识，将[300 000 000]写成一个数与整十整百数乘积，这就是该数的科学计数法表示.对于[25 000 000 000 000]，更多地会将它写成[=25×1 000 000 000 000]，这样写也有一定的简便作用，但这并不符合科学记数法的要求.怎样才能让学生体会到[a×10n]中字母[1≤a<10]的范圍要求的必要性，就出现了第3题.[265 900]可以表示成[2 659×102]，虽然已经写成一个数与10的乘方的积的形式，但是没有将这一大数简洁地表示出来.如何才能简洁表示，还能统一标准吗？a的范围的讨论势在必行.“把下列数表示成一个数与10的乘方的积的形式”这一环节的设计就像在乘方和科学记数法之间搭建了一座桥梁，紧紧地连接了“乘方”这一生长点.

“任何真正的认识都是以主体已有的知识和经验为基础的主动建构.”这一观点已经得到教师的广泛认同.在帮助学生“主动建构”的过程中，我们不仅要关注学生已有的外部经验，也要多关注数学内部经验的运用.学生经验的调用从“教”与“学”的角度看都体现学生思维从低到高的发展过程，搭建知识桥梁，建构数学知识体系.

不同教师对初中数学的知识储备并无显著的差异，关键在于能否想得到、用得好.“想得到”“用得好”的关键在于教师能否对学生的认知困惑处和关键点有准确的评估与判断.只有找准学生的认知困惑点、疑难处，才会有意识、有针对性地寻找“生长点”.

不走寻常路，找准“生长点”，才能让知识建构过程更自然、高效，让课堂绽放光彩.

[   参   考   文   献   ]

[1]  陈春燕.基于问题设计 落实核心素养[J].中学数学教学参考，2018（17）：5-7.

[2]  潘小梅.关于运算教学的若干思考[J].中学数学教学参考，2016（29）：6-9.

（责任编辑 黄桂坚）