基于表面增强拉曼光谱技术和GWO-SVR算法快速实现水中总氮总磷含量检测

张燕君， 康成龙， 柳雅倩， 付兴虎， 张金霄， 王明学， 杨刘震

燕山大学信息科学与工程学院， 河北省特种光纤与光纤传感重点实验室， 河北 秦皇岛 066004

引 言

随着科技不断地发展， 人类活动范围不断地扩大， 生活污水、 工业和农业废水的排放量激增， 从而对环境的影响也越来越严重， 其中水质污染尤其严重。 水中总氮(total nitrogen， TN)、 总磷(total phosphorus， TP)是评价水体受到污染严重程度的关键性指标[1]之一。 当水域中TN、 TP含量过高时， 会造成水体富营养化严重， 致使藻类和浮游生物过度繁殖， 水体透明度下降， 水质甚至会恶化至有害的程度， 最终对人类的生活产生危害， 因此快速准确测定水体中TN、 TP的含量十分必要。

目前对于TN、 TP测定的常规方法有很多， 比如国家标准法即碱性过硫酸钾氧化-紫外分光光度法[2]和钼酸铵分光光度法。 但是这些方法适用范围较小， 操作繁琐， 对实验环境要求高且检测时间长。 近年来光谱技术在水质检测领域得到广泛的应用， 在检测重金属离子浓度[3]和COD含量[4]方面较为成熟， 但在水中氮磷含量检测[5]方面少有报道。 而SERS技术[6-7]能够实现快速检测， 操作简单， 相较于普通拉曼光谱技术， SERS技术通过制备金属纳米粒子(如Au， Ag和Cu等)作为增强基底来吸附待测溶液中某些分子， 实现拉曼信号增强， 增强效果甚至可以达到104～106倍， 并且SERS频道窄， 水溶液对光谱信号干扰弱， 可检测到的光谱信息丰富， 非常适用于水质的在线快速检测[8]。 为了满足水中氮磷含量检测的高精度、 高效率等要求， 本文提出应用SERS 技术结合灰狼优化支持向量回归(grey wolf optimizer-support vector regression， GWO-SVR)算法建立水中氮磷浓度预测模型。 SVR在处理非线性回归问题上是一种比较高效优越的算法， 将其与其他智能算法相结合会使得预测模型更加准确高效。 GWO通过优化SVR的惩罚因子C和核参数g建立训练模型， 避免了陷入过拟合和局部最优等问题， 提高了模型的预测精度。

1 算法原理

1.1 支持向量回归算法

支持向量回归(SVR)是在支持向量机(support vector machine， SVM)基础上扩展出来的一种监督性机器学习算法， 用于处理数据回归预测方面的问题[9]。 对于给定的样本数据{(xi,yi),i=1, 2, …,n}xi∈Rn,yi∈Rn这里xi∈Rn是第i个样本的输入值，yi∈Rn是第i个样本的输出值，n为训练样本的数目， 假定回归函数为

f(x)=ωφ(x)+b

(1)

式(1)中，φ(x)为非线性映射函数，ω和b为要求解的参数。

(2)

式(2)中， ‖ω‖2为惩罚函数；C为惩罚因子， 训练误差受C影响；g则影响着回归函数的精度。 因此C和g是评价函数的重要指标， 也是GWO算法要进行寻优的两个参数。

(3)

(4)

(5)

1.2 灰狼优化算法

灰狼优化算法(GWO)是一种群体智能优化算法， 该算法模拟了自然界中灰狼的狩猎机制和领导等级[11]。 在建立灰狼等级模型时， 将具有最优适应度值的狼群个体依次标记为α，β，δ， 剩下的标记为ω。 在寻优过程中， 首先由三只头狼α，β，δ搜寻猎物位置， 逐渐接近猎物， 然后带领ω包围目标。

D=|CXp(t)-X(t)|

(6)

X(t+1)=XP(t)-AD

(7)

式(6)和式(7)中，t为当前迭代次数，A和C为协同系数向量；Xp是猎物位置；X表示当前灰狼位置。 当狼群开始包围猎物时， 随着目标猎物位置发生变化，α，β，δ的位置也在不断的迭代变化， 为获取最优值更新公式为

(8)

(9)

(10)

式(8)—式(10)中，Xα(t)，Xβ(t)和Xδ(t)分别是当前种群迭代t次后α，β，δ位置向量；Dα,Dβ,Dδ分别表示迭代t次后当前候选灰狼与最优三条狼的之间距离；X(t+1)为迭代t+1次后灰狼的位置。 灰狼群通过迭代过程不断地更新位置， 逐步的逼近猎物， 直到算法迭代完成， 成功捕获猎物获取最优解。

1.3 GWO-SVR模型的建立

GWO-SVR算法[12]的核心思想是利用GWO的快速搜索能力， 实现对SVR参数的自动优化， 以提升模型的预测效果[13]。 首先根据所建模型需求确定输入数据和输出数据并对数据集进行预处理。 然后对GWO算法设置初始化参数， 初始化狼群数量M=20， 迭代次数T=10。 根据要优化的模型和数据集的需求设置对应SVR模型的可调节参数数目和参数的取值范围， 本文SVR所要优化的参数为C和g， 取值范围为0.01～100。

适应度函数是评价参数性能的重要指标， 选取SVR算法训练集样本的均方误差(MSE)作为适应度函数， MSE的数值越小则认为目标参数值越优， 适应度函数式为

(11)

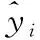
图1 GWO-SVR算法流程图

2 实验部分

2.1 仪器和样本

实验使用的仪器是必达泰克公司生产的BWS465-785S便携式拉曼光谱仪， 选取激发波长785 nm作为激发光源， 激发功率设置为300 mW， 在光谱范围为175～3 200 cm-1范围内对待测样本进行测量， 积分时间设置为10 000 ms, 每个样本检测3次取平均值。 配合光谱仪自带软件BWRam4TM进行光谱预处理， 然后采集光谱数据获取光谱特征值建立模型， 测试其预测功能并分析。

实验采用的TN和TP标准液为环境保护部标准样品， 用18兆欧超纯水将TN和TP样本溶液分别稀释配制成不同浓度梯度的待测溶液。 TN和TP浓度范围分为1.5～15和2～15 μg·mL-1， 样本数为26和23。 对每个配制样本充分混合均匀， 放在10 mL离心管中密封避光保存。

2.2 纳米银溶胶的制备

硝酸银(AgNO3)和柠檬酸钠(C7H5Na3O7)购置于国药集团化学试剂有限公司。 取1 mL浓度为1%的硝酸银溶液于锥形瓶中并用超纯水定容至200 mL， 进行加热并不断搅拌， 使硝酸银充分溶解。 当水沸腾后迅速加入3 mL浓度为1%的柠檬酸钠溶液， 继续加热搅拌60 min， 直到变化为乳白色即银溶胶制备完成。 将制备好的银溶胶放置高硼硅试剂瓶中冷却至室温后， 4 ℃冷藏保存。

2.3 方法

用一次性滴管吸取配制好的样本溶液2 mL滴入试管中， 然后吸取配制好的银溶胶1 mL缓慢滴入试管中， 轻晃摇匀， 避光静置30 min， 使其充分混合后进行检测。 实验时， 打开激光拉曼光谱仪预热15 min， 然后将配制好的加入了银溶胶的待测溶液用一次性滴管取3 mL放入比色皿中， 盖上遮光罩制造黑暗环境进行检测。 为使SERS基底增强效果理想化， 现通过对比实验探究基底与待测溶液的最佳体积混合比。 将TN和TP分别与银溶胶进行1∶1， 1∶2， 1∶3， 2∶1， 3∶1的体积比混合， 静置30 min后观察其拉曼图谱。 图2(a)和(b)分别为不同比例TN和TP的SERS光谱图。 由图可知在相同条件下， TN和TP溶液均与银溶胶以2∶1混合时增强效果最好。

图2 表面增强拉曼光谱图

TN和TP的主要拉曼特征峰的相关信息见表1和表2。 在检测浓度范围内光谱中特征峰的峰值强度会随着分子式基团浓度的改变而改变， 峰值强度越高表示此处物质含量越高。 通过配制不同浓度梯度溶液加入银溶胶进行检测， 得到TN和TP溶液能检测到特征峰的最低浓度分别为1.5和2 μg·mL-1， 当继续降低待测溶液浓度时并不能检测到明显的特征峰。 实验检测选取稳定性较好的TN溶液948.90 cm-1处特征峰和TP溶液930.44 cm-1处特征峰的峰值强度作为训练模型的输入值， 以其对应的浓度值作为模型的输出值。

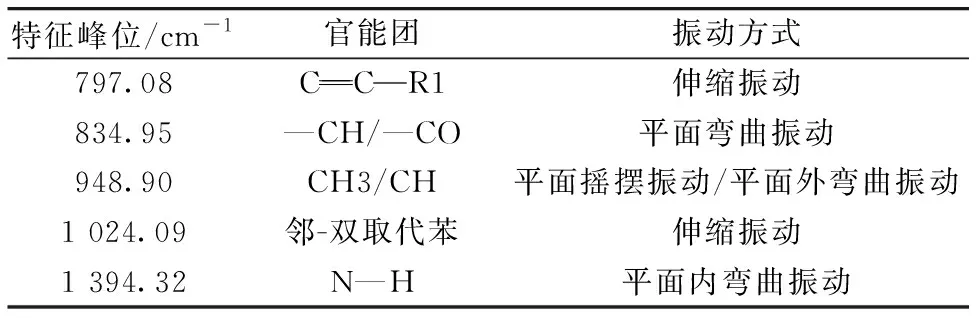
表1 TN的拉曼光谱特征峰

表2 TP的拉曼光谱特征峰

2.4 光谱预处理

在实验过程中， 由于受到样本的荧光背景和仪器的系统噪声影响， 光谱图出现基线漂移和峰值淹没导致光谱信噪比降低， 所以需对光谱进行预处理。 本文采用暗电流扣除、 光谱背景扣除(基线校正)和光谱平滑对原始光谱进行预处理， 各光谱在测量之前用BWRam4TM软件去除暗电流。 图3(a)为原始光谱和进行光谱背景扣除(基线校正)后的光谱。 图3(b)为光谱平滑处理， 选用Savitzky-Golay Filters平滑法进行光谱平滑处理， 窗口尺寸大小选择5作为光谱平滑的数据点。

图3 光谱预处理

3 结果与讨论

分别从配制好的TN和TP样本溶液中选取8组和7组作为测试集， 剩余溶液作为训练集。 将处理过的训练集峰值强度作为模型的输入， TN和TP溶液浓度为输出建立GWO-SVR浓度预测模型。

GWO-SVR定量分析模型对TN和TP测试集预测结果模型评价如表3所示。 基于模型的实际值和预测值之间的相关度结果分析如图4所示。

表3 GWO-SVR模型评价结果

图4 预测值和真实值相关性比较

由表3可以看出， GWO-SVR定量模型得到的TN和TP溶液的相关度均高于0.998， MSE均低于0.04， 具有较好的精确度。 从图4可以看出， 模型的相关度极高， 预测值浓度和真实值浓度基本都落在同一点上， 而且建模时间均在2 s内， 具有良好的实时性。

将同组数据通过人工蜂群算法优化支持向量回归(ABC-SVR)和粒子群算法优化神经网络(PSO-BP)分别建模进行预测， 其中ABC-SVR模型初始蜂群规模M=20， 迭代次数T=10， 个体最大更新次数G=100， 蜜源数量为M/2； PSO-BP模型初始参数设置为粒子群规模M=200， 学习因子C1和C2均为1， 隐藏层节点数为13， 最大训练次数为40 000。 模型评价结果见表4和表5。 不同建模程序的相关度曲线见图5。

表4 不同模型预测结果对比(TN)

表5 不同模型预测结果对比(TP)

从表4和表5评价结果可知， ABC-SVR模型运行时间虽控制在2 s左右， 但其相关系数和均方误差评价结果均低于GWO-SVR模型和PSO-BP模型； 同样PSO-BP模型相关度均高于0.996， MSE均低于0.05， 评价结果略低于GWO-SVR模型， 但运行时间和GWO-SVR模型相差数倍。 结合图5分析来看， GWO-SVR定量分析模型对TN和TP溶度的预测有着更好的相关性。 综上来说， GWO-SVR模型既能保证较好的预测精度又能将运行时间控制在2 s内， 具有良好实时性。 而且相较于另外两种模型来说， 该模型有着更少的参数输入， 只需设置种群数量M和迭代次数T两个参数。 GWO对SVR进行优化， 可以在短时间内寻找到最优的全局最优参数组合(C，g)， 缩短了模型的运行时间， 提高了预测精度， 进而提升了模型的工作效率。 由此可见GWO-SVR建立的定量分析模型结合拉曼光谱可以很好地实现对不同浓度梯度的TN和TP溶液含量的预测， 为以后水质监测提供了新方法。

图5 不同模型相关性曲线

4 结 论

提出了一种以纳米银溶胶作为基底的SERS技术结合GWO-SVR混合优化算法实现对不同浓度TN和TP溶液的快速定量检测方法。 通过以测得溶液光谱强度作为输入值，溶液浓度作为输出建立模型。 经过暗电流扣除、 基线校正和光谱平滑三个步骤对原始数据进行预处理， 选取GWO优化算法对SVR算法的参数C和g进行寻优， 避免了局部最优和过拟合问题， 提升了收敛速度。 为做对比将同组数据代入ABC-SVR和PSO-BP模型中， 以相关系数、 均方误差和运行时间作为指标进行对比。 预测结果表明， GWO-SVR定量分析模型相关系数、 均方误差以及建模时间均优于其他两种模型， 相关系数高达0.998 5， 均方误差也控制在0.04以内， 说明该模型能较好的完成快速定量分析， 具备良好的实时性和更高的检测精度。 因此， 此方法可以适用于水中TN和TP含量的快速定量检测， 为今后水质检测提供了理论依据。