基于Blending 多卷积神经网络模型融合的滚动轴承声学故障诊断方法

余龙靖，王 冉 ，刘丰恺

（上海海事大学 物流工程学院，上海 201306）

0 引言

滚动轴承是工业设备中最重要的部件之一，其故障会立即危及机械设备的特性[1]，因此对滚动轴承的故障诊断具有关键的意义。传统方法使用单独传感器的精确测量信号进行诊断；但是，由于单个传感器给出的故障信息比较有限，不能完全反映被测目标的故障情况，因此必须采用多个传感器对滚动轴承的故障信息进行采集和融合[2]。

随着深度学习(Deep learning)技术的发展，利用深度学习实现特征提取自动化和端对端的故障诊断方法，将预处理、特征提取、特征分类整合到一起，可以很好地进行故障诊断[3-5]。Guo 等[6]使用深度自编码器模型(DAE)提取轴承振动信号的时域与频域特征故障进行诊断；Lu 等[7]利用卷积神经网络(DCNN)进行滚动轴承的故障诊断，并验证了该方法在噪声存在时的有效性和适应性。Zhang 等[8]使用深度卷积和实体模型对故障滚动轴承进行诊断，立即求解振动信号，并通过融合域响应方法进行域转移，提高了实体模型诊断的实际效果。

目前，基于振动信号的测量分析方法由于其信息丰富、物理意义明确、易于识别和决策，已成为最常用和有效的方法之一。然而，在很多实际情况下，一方面由于设备或工作环境的限制，振动传感器的安装不方便；另一方面，在高温、高湿、高腐蚀和有毒的环境中，振动信号不易测量，这限制了振动诊断方法。

基于声学的诊断(ABD)技术可以绕过这一限制。在这种情况下，可以采集设备的声信号并应用于故障诊断[8]。声学故障诊断技术具有仪器测量简单、非接触测量、不影响设备正常运行等特点，因此在故障诊断中得到了应用。然而，在缺乏先验知识的情况下，传统的声学诊断方法难以确定合适的测量位置。根据多通道分析，由于被测位置的不确定性，ABD 方法仅使用了部分声学信息，在诊断上存在一定的不足[9]。精确阵列测量的ABD 技术，根据多通道声学信号的同步精确测量和分析，可以获得详细的声场布局信息，解决多通道精确测量带来的信号不稳定和局部诊断的缺点。众所周知，多信号的融合大多停留在数据信息级权重计算融合环节，权重值明确，整个过程复杂，实用性较差[10]。融合后，仍需利用信号分析技术进一步获取故障特征，区分管理决策。整个诊断过程复杂，需要高信号分辨率技术和工程项目社会经验。此外，由于声信号是非接触测量，测得的信号在背景噪声的影响下往往信噪比较低，所以使用单一模型进行故障诊断的效果往往较差。

针对上述问题，本研究提出基于多卷积神经网络模型融合的滚动轴承声学故障诊断方法，以达到提高诊断精度的目的。模型融合是将多个弱模型，通过一定的组合方式，组合成一个强模型的方法[11]，其主要的方法有从决策结果融合、Stacking 和Blending 等，由于Blending 的方法在第二阶段使用了与第一阶段不同的训练数据，有效地避开了信息泄露的问题。由于不需要进行kfold 交叉验证，Blending 在实现起来比较简单。因此，本研究利用3 个深度卷积网络对3 通道传声器信号进行处理，利用Blending 模型融合方法对CNN 进行集成，最终实现滚动轴承的非接触式故障诊断。

1 基于Blending 的多CNN 模型融合

1.1 Blending 模型融合

为了解决单一模型进行故障诊断结果的不确定性，通过使用Blending 模型融合的方法对多个深度神经网络进行融合以提升整体性能。Blending是集成学习(Ensemble learning)的一种模型融合方式，直接将不相交的数据集用于不同层的训练，可有效地避免信息泄露的问题。

平均Blending 是最简单的一种方法。其定义为：已知多个弱学习器(g1,g2,g3,···,gt,···,gn)，每个gt的权重相同。对于分类问题：

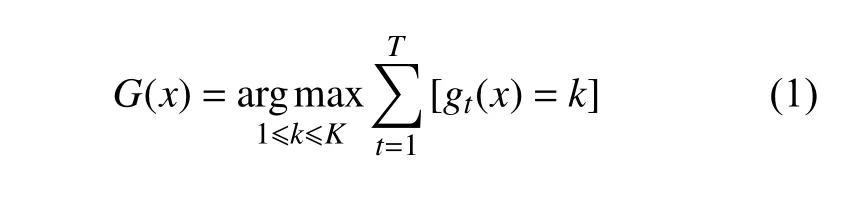
其中，G(x)代表融合后的模型，K为Label 类别值。本研究采用的是一个二层的Blending 模型，其原理结构如图1 所示。

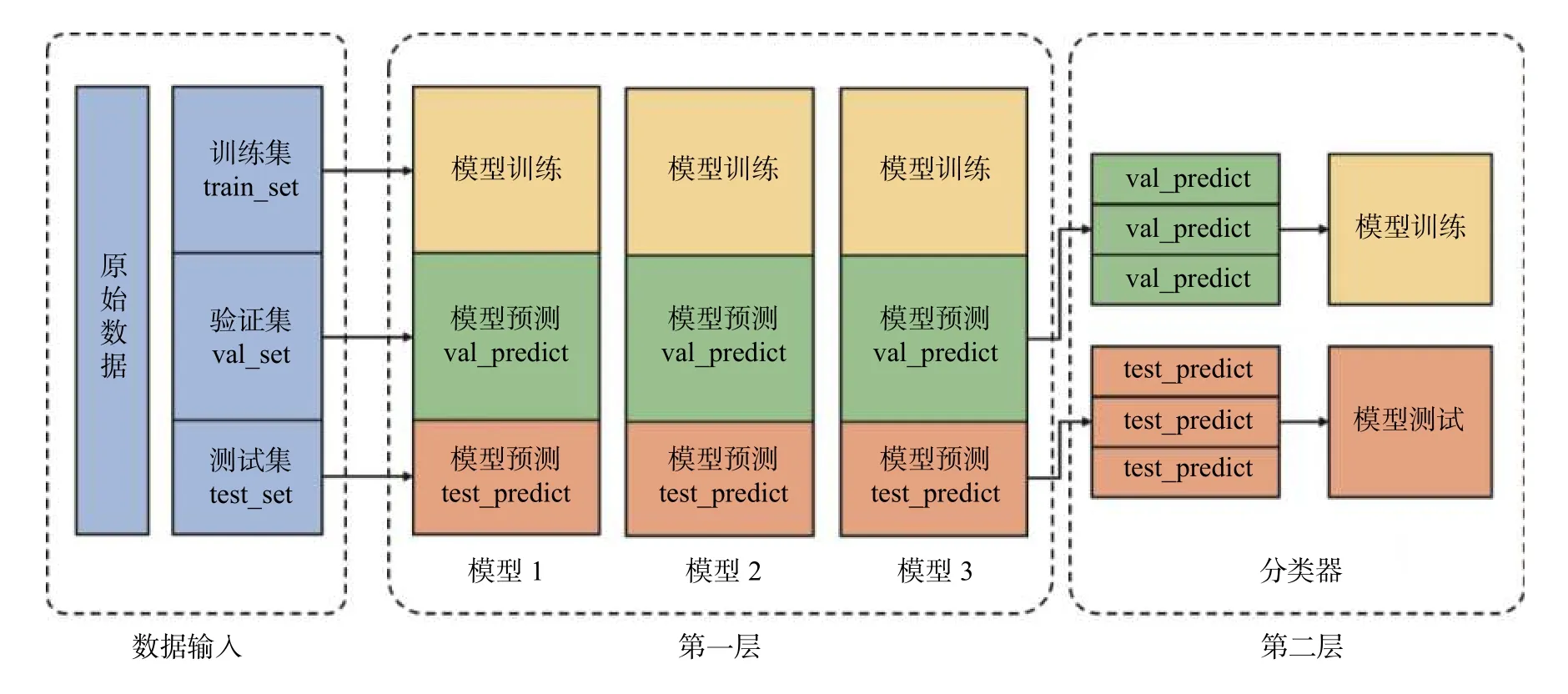
图1 Blending 原理结构图Fig.1 Structural diagram of Blending principle

Blending 的具体实现步骤为：

1）将数据分为训练集和测试集(test_set)，其中训练集需要再次分为训练集(train_set)和验证集(val_set)。

2）创建第一层的多个模型，可以是同构的，也可以是异构的。

3）在步骤2 中使用train_set 训练几个模型，然后使用训练好的模型预测val_set 和test_set，得到val_predict 和test _ predict。

4）创建第二层模型，并使用val_predict 作为训练集来训练第二层模型。

5）用第二层训练的模型预测第二层测试集test_predict，结果就是整个测试集的结果。

1.2 卷积神经网络（CNN）

在本研究中，双层Blending 模型的第一层的多个模型采用了多个卷积神经网络。作为深度神经网络中的关键实体模型之一，卷积神经网络（CNN）在语音识别技术、图像处理和故障检测等行业得到了极大的提升[12]。

卷积神经元网络实体模型包括3 个实体层，分别是卷积层、池化层和全连接层。在卷积层中，利用几个卷积核和一个偏置激活函数对输入进行卷积，可以得到一系列的特征图。整个卷积过程的公式为：

式中：x表示卷积层的输出。池化层通常在卷积层之后连接，以降低特征的维数的同时特征极限在一定水平上保持不变。常见的池化方法有最大池化、平均池化和随机池化等。池化层一般只进行降维，没有主要参数，不需要升级权重值。在pooling 层上，卷积层输出的feature map 被pooling到每个不重叠的区域，并选择每个区域的最大值或平均值，最终使输出的图像在2 个维度上减少。

输入数据信息按照几个卷积层和池化层进行传播后，根据全连接层的特点进行分类。在全连接层，通过特征图计算所有一维矩阵的特征值和激活函数的权重：

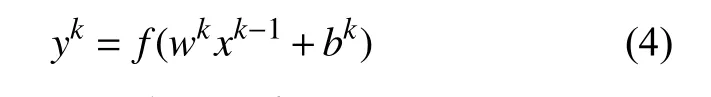
式中：k为网络层的序号；yk为全连接层的输出；xk-1是展开的一维特征向量；wk为权重系数；bk为偏置项。激活函数f(·)常使用是Softmax，是一种适用于分类任务的激活函数。

在进行过网络的前向传播后，需要进行反向参数更新过程更新权重系数wk与偏置项bk。对于一个CNN 网络，其训练目标为最小化网络的损失函数值，故损失函数作为反向参数更新过程的目标函数，其选择十分重要。常见的损失函数包括均方误差、交叉熵、负对数似然函数等。为了更好地获得更强的实际效果，采用交叉熵作为损失函数进行反向传播，其关系如下

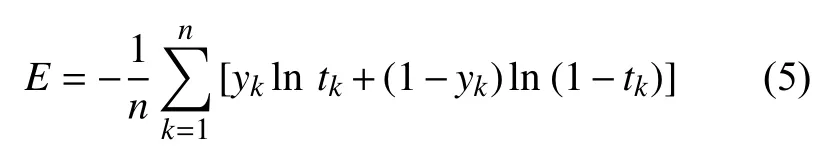
其中：n为此类故障的样本量；t为估计值；y为真实值。在整个训练过程中，最小化损失函数的方式是梯度下降法。根据式（5），可以得到一阶偏导数，逐步迭代卷积和神经元网络的主要参数（：wk、bk）。

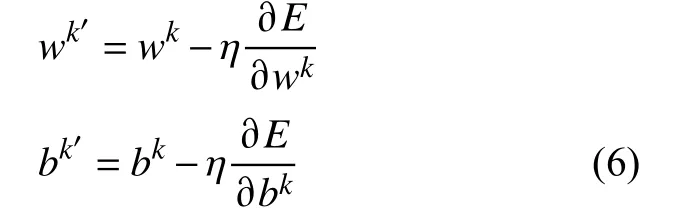
本研究采用3 个不同网络结构和参数的CNN模型，其模型结构参数如表1 所示。3 个CNN 模型中模型层数与参数都不相同，其中CNN1 采用的这样可以在对同一预测目标进行预测时得到不一样的效果，进而可经过Blending 将3 个模型融合得到具有更好预测效果的模型。

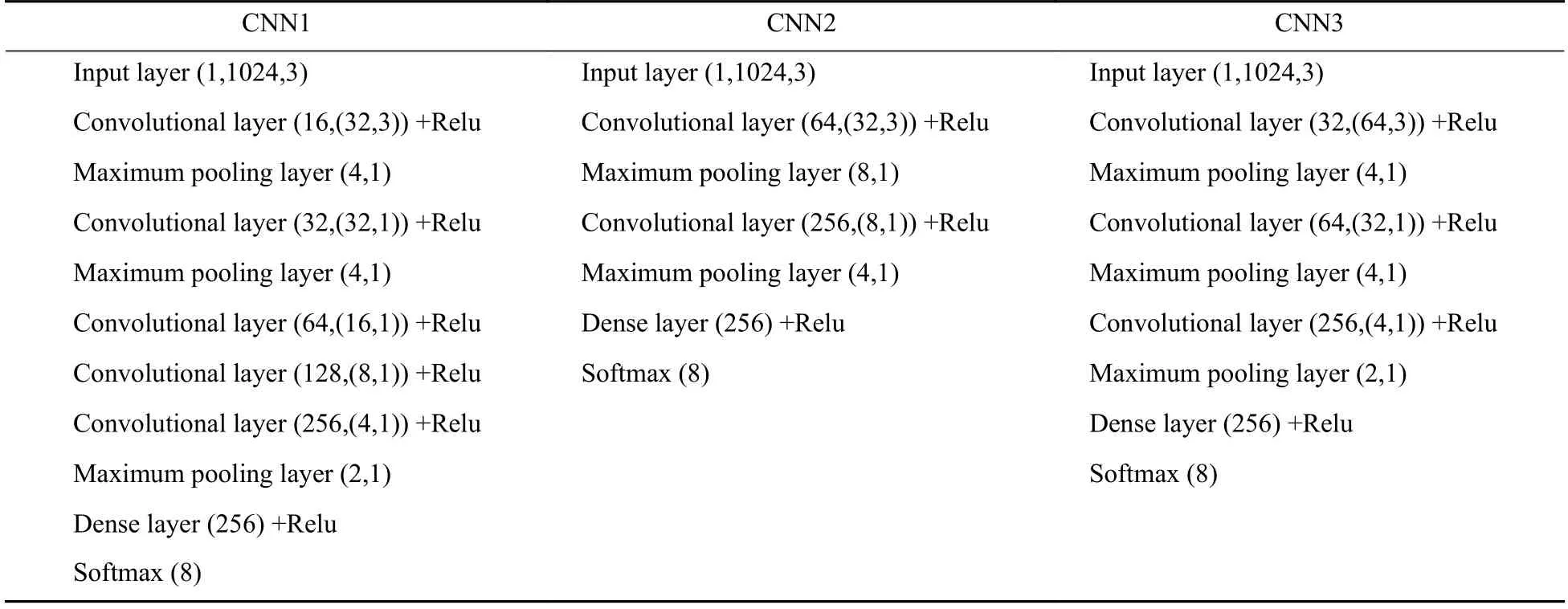
表1 CNN 结构参数Table 1 CNN structures and parameters

1.3 多CNN 的Blending 融合模型

融合模型流程图如图2 所示。针对滚动轴承故障诊断中单一传感器信息的不全面性，采用不同位置的3 个传感器的原始信号。原始数据的37.5%设置为训练集，用于模型第一层的多CNN模型进行训练，利用CNN 的结构将3 个传感器的信号堆叠为3 通道信号输入训练以实现多通道信息融合，以保证信息的全面性。

图2 CNN 的Blending 融合模型Fig.2 Blending fusion model of CNN

之后将原始数据的37.5%作为验证集，25%作为测试集分别输入训练好的CNN 模型中，将3 个CNN 的预测结果val_predict 作为第二层模型的训练集，并将预测结果test_predict 作为第二层模型的测试集验证整个模型的诊断效果。

2 实验验证

2.1 实验设置

为了证实模型的有效性，采用如图3 所示的滚动轴承实验台的3 个传声器采集的声信号数据对提出的模型进行验证。轴承实验台的尺寸为68 cm×58 cm×80 cm，主要包含基座、油路系统、电机、轴承、轴承固定部件及加载装置。在电机的驱动下，联轴器带动转子旋转从而能带动轴承内圈随着转子转动，转频约为12 Hz。轴承的外圈通过夹具固定，并且通过加载装置施以适中的载荷。

图3 滚动轴承实验台Fig.3 Rolling bearing test rig

采用电火花加工方式分别在轴承试件的外圈、内圈、滚动体上加工点蚀故障。沿轴承实验台的轴向布置了3 个参考传声器，从而保留每扫描一步的相位信息。3 个参考传声器按照从右向左的顺序进行编号，分别为1、2、3 号，其中最右边的1 号传声器距离测试轴承最近。传声器的采样频率为4096 Hz。

2.2 数据预处理

为了能更好地反映出故障冲击，选用7 级载荷的3 个原始传声器数据进行验证。为了更好地反映模型的抗噪性，对原始的传声器信号叠加了信噪比为-10 dB 的高斯白噪声，用以模拟真实强干扰情况下的诊断。表2 为采集到的信号的故障类型。故障类型共有8 种，分别为正常、滚动体故障、内圈轻微故障、内圈中等故障、内圈严重故障、外圈轻微故障、外圈中等故障、外圈严重故障。

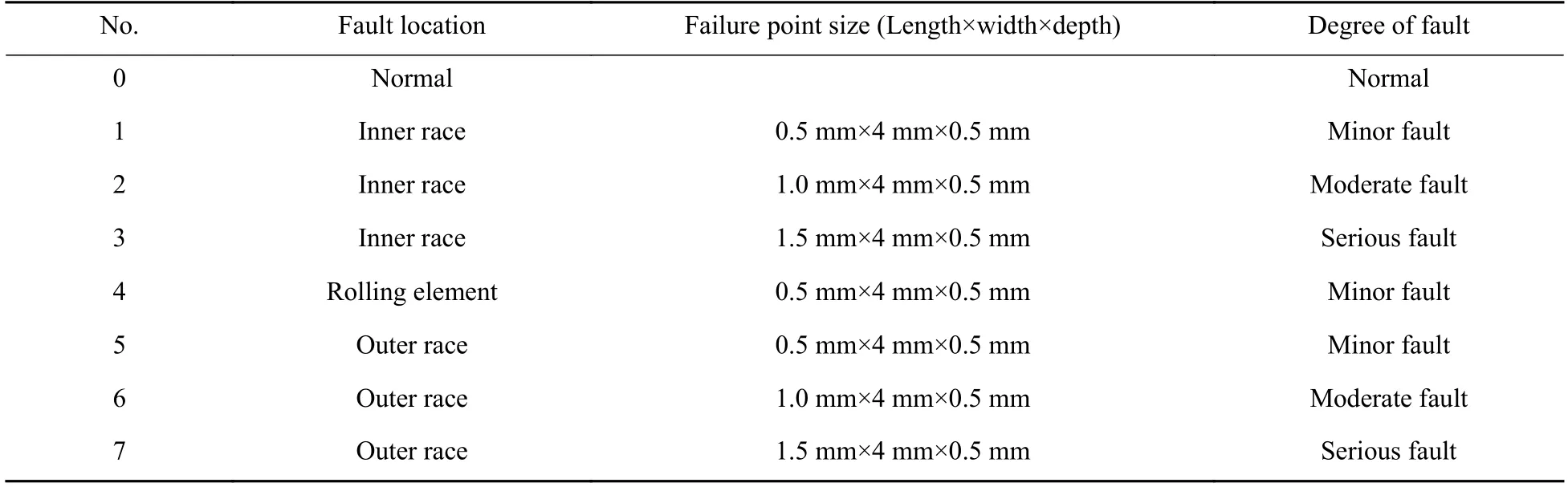
表2 试验轴承故障类型Table 2 Failure types of test bearing

对于每一种故障类型，采集到的10 个时间长度为26 s 的声信号文件，以样本长度为0.25 s（即1024 个数据点）采样，共可得到每类故障各1000 个样本，每个样本的时域波形如图4 所示。对于每类故障类型的样本，利用One-hot 的形式将其标记标签。例如，对于滚动体故障样本，利用One-hot 将其标记为00001000。

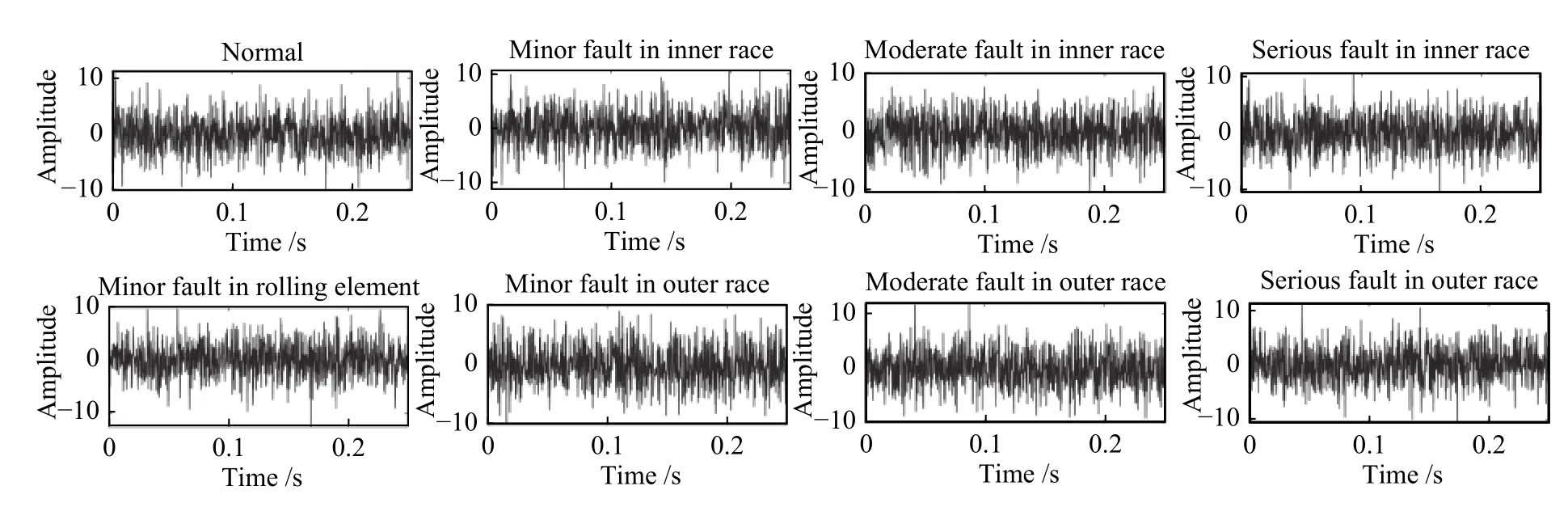
图4 样本波形示意图Fig.4 Schametic map of sample waveform

在获得的8000 个样本中，37.5%的样本（即3000 个样本）划分为训练集，37.5%的样本（即3000 个样本）划分为验证集，25%的样本（即2000 个样本）划分为测试集。获得不同故障的训练、验证和测试样本后进行归一化处理，归一化公式为：

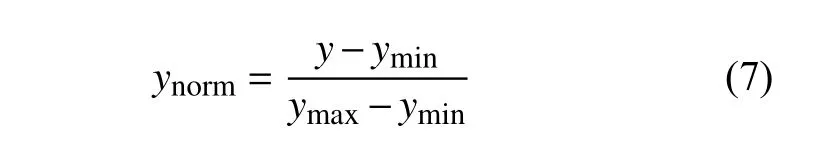
式中：y表示原始数据，ynorm表 示归一化后的数据，ymax、ymin分别表示原始数据的最大值和最小值。对3 个传声器采得的数据都使用上述方式进行数据预处理。

2.3 结果分析

将处理好的样本数据放入搭建好的融合模型中进行两层Blending 的训练。首先，利用训练集数据分别训练3 个CNN 模型，对数据进行自适应特征提取。如图5 所示，为了更好地展示CNN 实体模型自适应特征提取的实际效果，采用T-SNE对自适应提取的特征和原始输入数据信息进行分析。

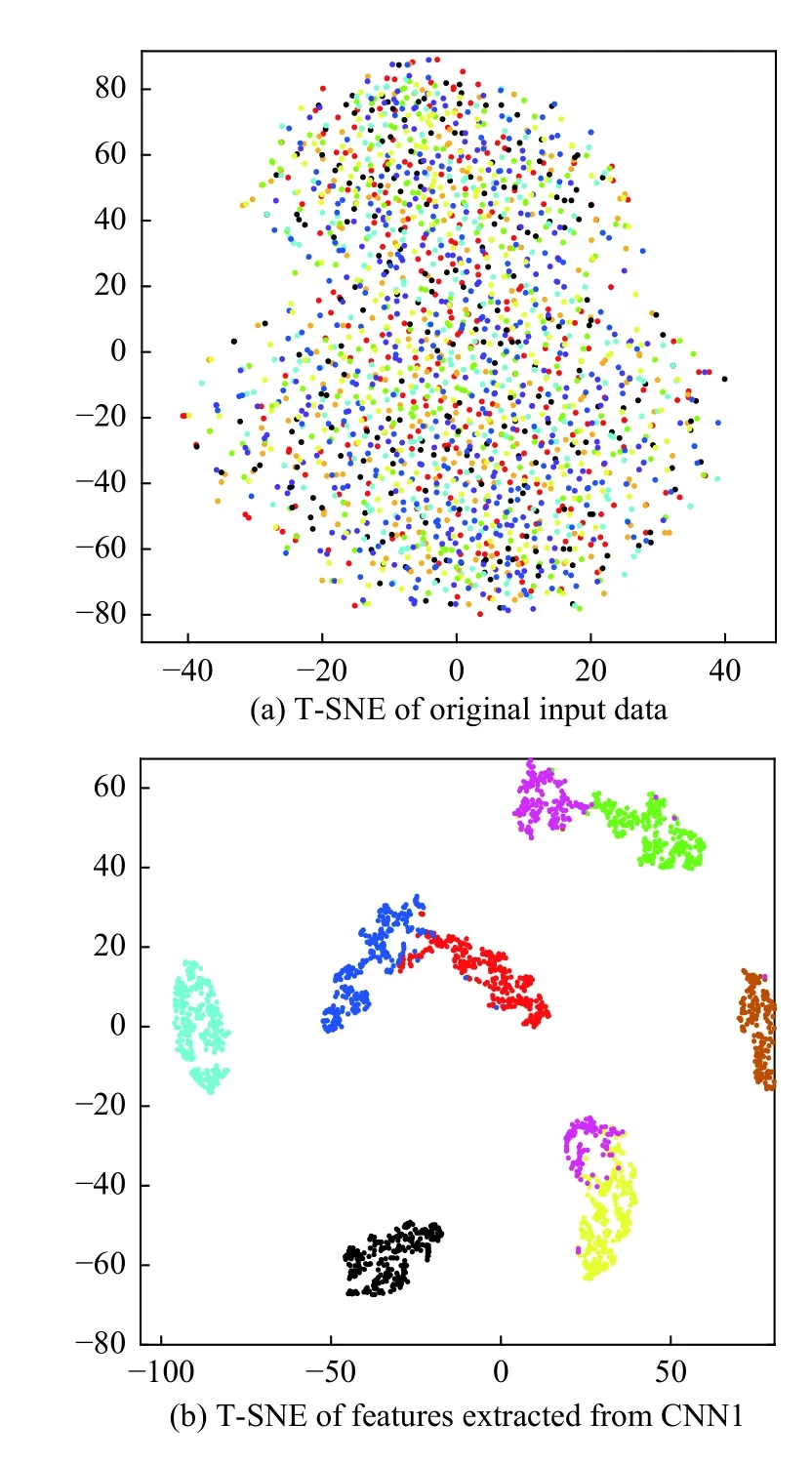
图5 CNN 特征提取T-SNE 可视化Fig.5 T-SNE visualization of CNN feature extraction

图5 分别为原始输入数据和第1 个CNN 自适应提取的特征。根据T-SNE 结果可知，CNN 模型能够自适应地从原始时域声信号中学习到具有可分性的特征，从而为滚动轴承的故障诊断提供基础。但是，由图5b 中还可以看出，尽管当输入传声器信号的信噪比较高时，单个CNN 训练下得到的特征整体上具有一定的可分性，然而由于单个故障形式存在多种故障程度，所以在某些故障类型仍然存在一定的误分情况。因此，使用单个CNN 进行故障诊断存在一定的不确定性，且实际中不易选择合适的传声器测点。

然后，将融合模型第1 层输出的验证集预测结果和测试集的验证结果输入第2 层进行训练验证，其训练曲线如图6 所示。可见，融合模型的训练曲线非常光滑，收敛速度快。从图7 中的混淆矩阵可以看出，融合模型对各种故障类型均有较高的诊断精度，平均诊断精度达到97.46%。

图6 融合模型训练曲线Fig.6 Training curves of Fusion model

图7 融合模型混淆矩阵Fig.7 Confusion matrix of fusion model

2.4 诊断结果对比

为了证明所提出的方法对于声学故障诊断的效果优于其他方法，利用不同方法对声信号样本进行故障诊断并对比其结果。

首先，为了证明卷积神经网络对比其他机器学习算法在噪声干扰下声学故障诊断的优越性，采用支持向量机(SVM)[13]、随机森林法(RF)[14]、多层感知机(MLP)[15]对数据进行训练诊断。采用2.2 节同样的样本构造方法构造500 个长度为0.25 s的样本并对其标记标签。将处理好的样本分别输入SVM、RF、MLP 网络进行训练，得到的预测精度分别为80.86%、85.45%、89.60%。而利用单个CNN 进行诊断的效果均高于90%。由此可证明CNN 的优越性。

表3 是融合模型与单个CNN 模型以及其他常用浅层机器学习模型诊断结果的对比。可见：3个单独的CNN 在自适应提取特征后，经过 Softmax初步分类的平均诊断精度为93.43%；利用Blending融合后，诊断精度达到97.46%，相比于未融合前CNN1 诊断精度92.55%提高了4.91%。CNN2 诊断精度94.65%提高了2.81%，CNN3 诊断精度93.10%提高了4.36%。

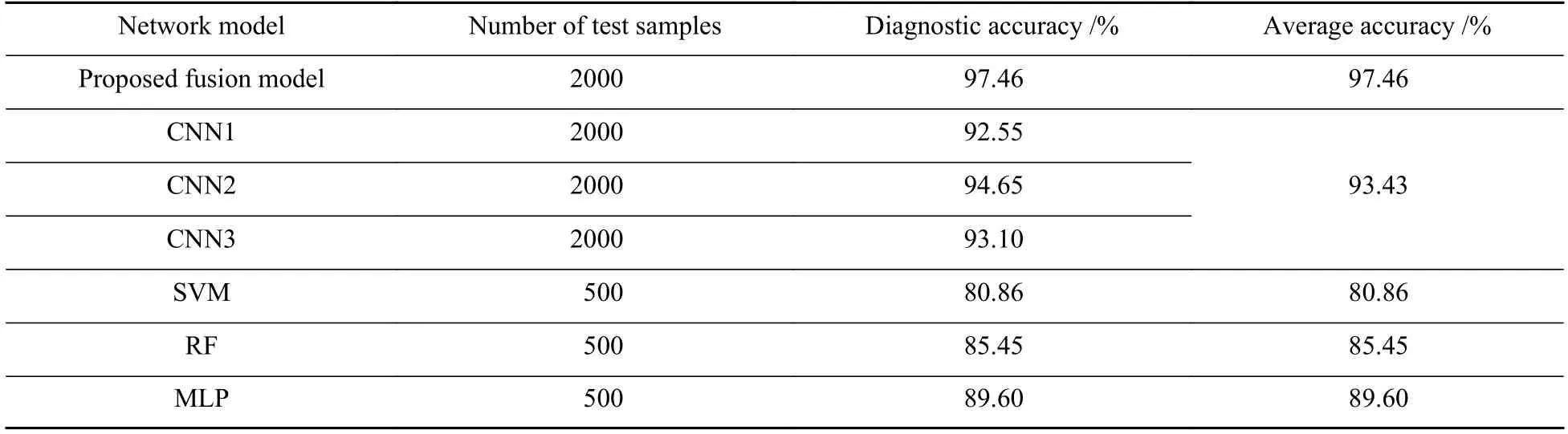
表3 融合结果对比Table 3 Comparison of fusion results

图8 是对于各模型的诊断结果的总结。对比CNN 与SVM、RF、MLP 的结果可以看出，CNN 的诊断结果均高于90%，而其他机器学习方法的诊断精度均低于90%，可知利用卷积神经网络对于强干扰下的声信号进行故障诊断的效果明显好于其他传统机器学习方法。再者，对比融合模型与单个CNN 模型的诊断精度，由于融合模型结合了第一层多个卷积神经网络的诊断结果用于第二层的学习，故可以有效避免单个网络模型在诊断上的不确定性，增加了网络的容错率，从而提高诊断精度，正如结果可见，融合模型的诊断精度提升了近4%，这对于声信号的故障诊断的效果有较大的提升。

图8 诊断结果对比Fig.8 Comparison of diagnostic results

综上所述，本研究提出的多深度学习模型Blending 融合的声学故障诊断方法具有较好的优越性和噪声下的鲁棒性。

3 结论

1）提出了一种基于Blending 多卷积神经网络模型融合的滚动轴承声学故障诊断方法，并且由于振动诊断方法在特殊情况下的局限性，采用了基于非接触测量模式的故障诊断方法。且利用多传声器融合在一定程度上可以克服声学诊断中不易选择传声器测点位置的问题。

2）利用融合多卷积神经网络对比其他机器学习模型在噪声干扰下对滚动轴承的声信号故障诊断具有更好的效果。半消声室滚动轴承故障诊断数据集验证结果显示，利用Blending 融合模型诊断的准确率高达97.46%，高于单一卷积神经网络的精度，证明了该方法的优越性。