铝合金盒形零件充液拉深工艺参数优化研究*

门向南，吕秀文，徐 勇，夏亮亮，李晓军，周 雄，陈 铭，张士宏

（1.航空工业成都飞机工业（集团）有限责任公司， 成都 610092；2.中国科学院金属研究所， 沈阳 110016；3.中国科学技术大学， 合肥 230022）

钣金零件在航空制造业中占有十分重要的地位。据统计，钣金零件约占飞机零件总数量的50%、飞机制造工作量的20%、飞机工艺装备数量的65%[1]，而多数钣金零件具有尺寸不一、形状复杂、品种多且数量少的特点。近年来随着我国航空工业的快速发展，钣金零件具有轻量化和整体化的发展趋势，由此对高强铝合金的需求不断增大。由于铝合金具有良好的抗腐蚀性能、机械性能和轻量化等优点，因此其广泛应用于航空钣金零件[2]。钣金零件采用传统落压成形工艺，会带来材料利用率低、废品多、零件精度差、模具寿命低等问题，并且铝、钛等航空航天常用金属材料的室温成形能力较差，导致在加工此类构件时，常出现起皱、开裂等缺陷，对传统成形工艺提出了巨大的挑战[1，3]。

充液拉深成形技术作为制造复杂形状薄壁板件的精密成形技术，能够大幅提高此类零件的成形极限，已经在航空航天装备制造工业中得到越来越广泛的应用[4-6]。板材充液拉深成形的基本原理是采用液体代替刚性凹模或凸模，作为传力介质传递载荷，使板材在液体压力作用下贴靠模具从而实现金属零件的成形[7-9]。通过合理加载流体压力，能够促进板材贴靠模具，既节省工序又发挥了材料的最大效能，具有制模简单、周期短、成本低、产品质量好、形状和尺寸精度高等特点[10]。

异形薄壁钣金构件多数是非轴对称结构形式，在航空领域中有广泛的应用，盒形零件就是其中典型的代表[11]。盒形零件在其成形过程中，侧边直角和底部圆角的变形是不均匀的，成形难度较大。盒形零件直角边的成形特点类似于弯曲成形，圆角处的成形类似筒形件拉深成形。由于直角和圆角变形区域之间存在联系，因此变形过程十分复杂[12-13]。为了获得较好成形质量的目标零件，国内外很多学者也对拉深成形过程进行了研究分析[14-17]。但是在实际的成形过程中，盒形零件的成形质量往往涉及多个参数间的交互作用，通过经验或者试错法来调整工艺参数的方法已无法满足盒形零件的高质量生产。通过使用一些先进的优化方法可以从大量数据中挖掘出有用的规律，这对于指导生产具有非常大的应用价值。

本文将以某航空铝合金薄壁盒形零件作为研究目标，通过使用有限元模型结合优化方法——响应面法（Response surface method，RSM）对该盒形零件的高效精确成形进行研究。通过Dynaform 5.9.3 有限元软件模拟目标零件的成形过程，并选取坯料圆角半径、压边力和液压力3 个工艺参数进行优化，以铝合金盒形零件的最大减薄率作为优化评价指标，选择中心复合设计法设计试验方案并通过有限元模拟获得不同工艺参数下模拟结果；基于响应面法对试验数据进行了分析，建立了关于盒形零件的最大减薄率与工艺参数之间二阶响应模型，并通过此模型获得了最佳工艺参数组合。最后通过实际充液拉深成形试验验证所建立的响应模型和优化后的工艺参数组合的可靠性。

零件特征及有限元模型

1 试验材料

本文采用的材料是热处理状态为O 态的2A16 铝合金板材，板材的厚度为1.2mm，所使用材料的化学成分如表1 所示。

表1 2A16 铝合金的化学成分（质量分数）Table 1 Chemical composition of 2A16 aluminum alloy (mass fraction) %

基于沿着与轧制方向呈0°、45°和90°方向的单向拉伸试验所获得的拉伸数据，并采用Swift 硬化模型对真应力-真应变曲线进行拟合，得到的2A16 铝合金力学性能参数如表2 所示。其中，材料泊松比为0.38，杨氏模量为69GPa，密度为2.7×10-9g/mm3。由强化系数k和加工硬化指数n的分析发现，2A16 铝合金的硬化行为近乎各向同性。因此，在模拟过程中，可采用0°方向上的硬化曲线作为输入。

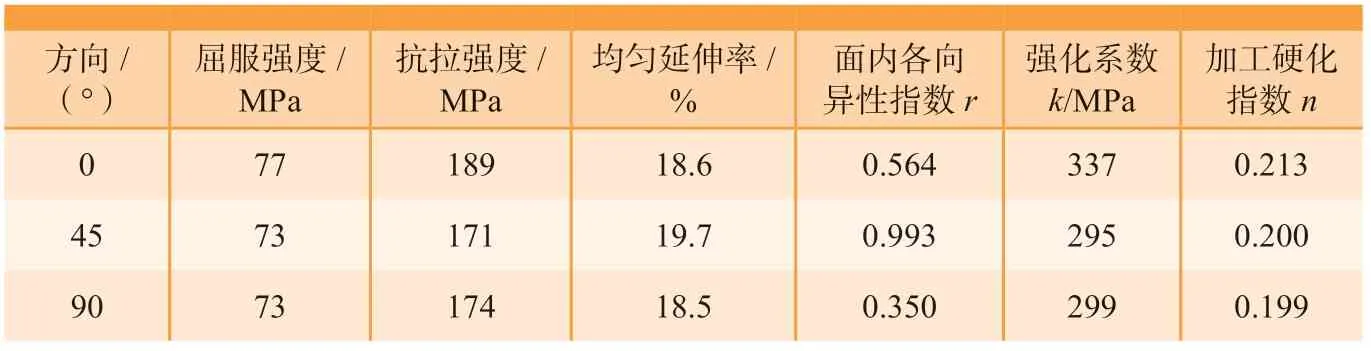
表2 2A16 铝合金的力学性能Table 2 Mechanical properties of 2A16 aluminum alloy

2 目标零件结构特征

盒形零件结构特征如图1 所示。其中，零件长度L=322.4mm，宽度B= 222.4mm，高度H0=68mm，底部圆角半径rp=21.2mm，侧壁圆角半径r=13.2mm。在实际成形中，为了保证液体的密封性及创造良好的拉深条件，设计法兰边作为工艺补充面，定法兰圆角半径rf=10mm，并考虑切除余量，所设计的最终成形目标零件的几何模型如图2 所示，最终拉深高度H=80mm，法兰边缘宽度D=24mm。

图1 盒形零件的结构尺寸（mm）Fig.1 Structure of box-shaped part (mm)

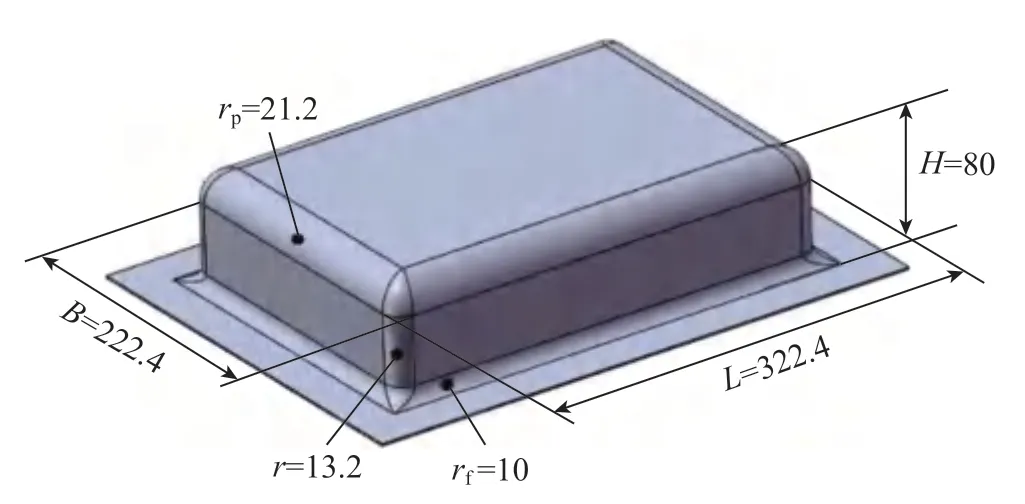
图2 成形目标零件的几何模型（mm）Fig.2 Geometric model of forming target part (mm)

3 有限元模型的建立

本文将采用被动式充液成形工艺对所述盒形件进行成形，即液体将以恒定压力（本文中简称为“液压力”）的方式作用于坯料底部，并在拉深过程中为板料提供一定的背应力，如图3 所示。

图3 成形工艺原理及有限元模型Fig.3 Forming process principle and finite element model

在盒形件的拉深过程中，坯料的形状设计对材料的流动以及最终的成形效果将产生极大的影响。对于盒形件而言，在已知零件几何模型尺寸的前提下，其初始坯料设计往往依托最终零件尺寸，并根据成形前后面积相等的假设，对最终盒形件进行展开。四周直边部分，一般按照弯曲变形处理，而圆角部分一般按照1/4 圆筒拉深变形进行处理[12]。此外，考虑到材料在成形过程中的流动性，坯料一般不采用直角矩形形状，而是采用带圆角的矩形坯料形状。本研究基于盒形件展开原则并结合现场预试验结果，将优化前的坯料形状设计如图4 所示。其中，长度a=488mm，宽度b=388mm，坯料圆角半径R1=71mm。坯料圆角半径R1对成形过程中的材料流动性影响最大，因此，后续将对该坯料圆角半径进行进一步的优化设计。

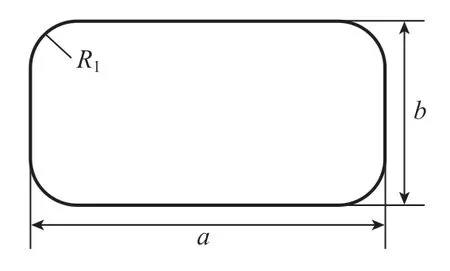
图4 坯料几何形状设计Fig.4 Design of blank geometry

使用有限元模拟软件Dynaform 5.9.3 对铝合金薄壁盒形零件的充液拉深过程进行模拟，盒形件拉深的有限元模型如图3（b）所示。模型中包括板料、凸模、凹模和压边圈4 个部分。在成形过程中，由于凸模、凹模和压边圈变形几乎为0，设置为刚体。模型有限元网格划分中网格类型选用四面体，板料单元设置为Belytschko-Tasy 壳单元，模具划分为刚性单元。网格大小设置为4mm×4mm，经过网格划分后板料共有11450 个单元，凸模共有8526个单元，凹模共有20274 个单元，压边圈共有8810 个单元。在所有模拟过程中，压边间隙均采用1.1 倍料厚，即1.32mm[4]。由于铝合金存在一定程度的各向异性，在模拟过程中，选取36 号材料模型（Barlat’s-3 Parameter Plasticity Model）对2A16铝合金的本构关系进行描述。其中材料的硬化行为采用Swift 硬化模型进行描述。其未知参数k和n通过拟合真应力-真应变曲线获得，具体值见表2。而屈服模型采用Barlat89屈服函数，其函数表达式如下：

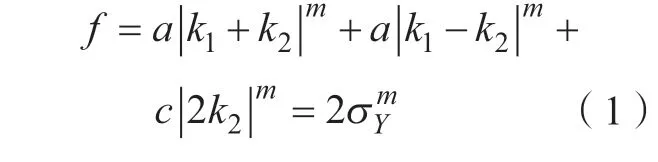
式中，σY为单轴屈服应力；k1=m为其幂指数，是与材料的晶体结构相关的数值；σ11为第一主应力；σ22为第二主应力；σ12为剪切应力；a、c、h和p为未知参数，并可通过0°、45°和90°方向上的厚向异性系数r0、r45、r90的值计算获得。具体计算方法如下：

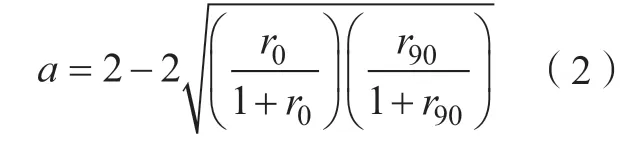
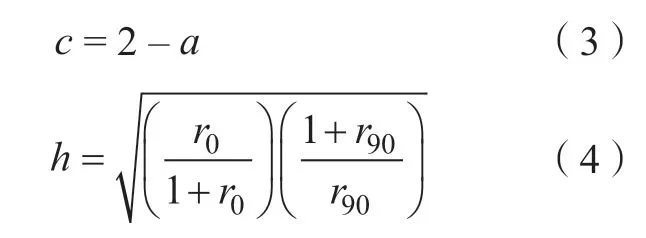
此外，参数p需通过显示迭代的方法获得。由Barlat 屈服函数可获得任意方向上的厚向异性系数rφ值的表达式为：

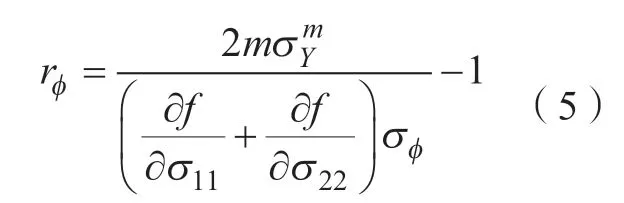
式中，σφ为任意φ角度下的单轴应力。当φ=45°时，可获得参数p关于r45表达式，并通过迭代获得p值。

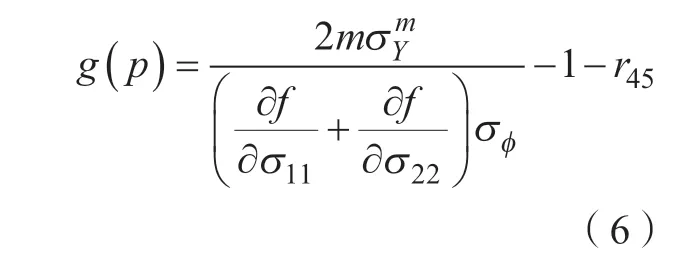
式中，m值的选取与材料的晶体结构类型有关，对于铝合金来说，其具有面心立方结构，m=8。此外，在进行材料模型的定义时，仅需输入密度、杨氏模量、泊松比、k值、n值、r0、r45和r90，即可建立硬化模型与屈服模型。

影响盒形零件成形的关键工艺参数

1 摩擦系数的确定

在实际成形过程中，模具与零件之间的摩擦系数对材料的流动具有显著影响。因此，在优化之前，需对摩擦系数进行选取。实际生产时，一般会使用润滑剂，Hu 等[18]研究了不同润滑剂 （包括PhoS、MoS2、PTFE、拉深油等）下摩擦系数所能达到的大概范围。依据其研究结果。在有限元模拟中，分别设置摩擦系数为0.025、0.050、0.075、0.100、0.125、0.150，旨在基于模拟所得结果指导实际成形过程中的润滑剂选择，其他参数包括坯料圆角半径、压边力和液压力等保持相同，得到不同摩擦系数下铝合金薄壁盒形零件的减薄率，结果如图5 所示，提取最大减薄率，得到如图6 所示的不同摩擦系数下该盒形零件的最大减薄率的变化趋势图，其中压边力P为4MPa，液压力F为7MPa。

从图6 中可以看出，当摩擦系数小于0.1 时，随着摩擦系数增大，该盒形零件减薄率不断减小，但减小幅度很小，可以认为影响很小；当摩擦系数大于0.1 时，该盒形零件的最大减薄率明显增加，当选取的摩擦系数为0.2 时，该盒形零件的最大减薄率为42.1%，此时该盒形零件已经发生了破裂。这是因为摩擦系数会影响板料的流动状态，摩擦系数大时，板料流动的阻力更大，在模具和压边圈之间对底部的补料不足，因此其最大减薄率急剧增加。考虑到摩擦系数较小时对润滑剂要求较高，因此，在后续的模拟中均设置摩擦系数为0.1。

2 单因素分析方案确定

由于成形过程中盒形零件容易出现起皱、破裂等缺陷，因此需要对一些工艺参数进行优化从而成形出质量较好的目标零件。已有研究表明，在盒形件的充液拉深过程中，最大减薄率总是出现在直壁圆角r和底部圆角rp交汇处，即底部4 个顶点圆角位置，并可能由于减薄过大而造成材料失效破裂[6，12，14-15]。其产生失效主要有两个原因：一是该区域材料流动困难，很难得到周边的补料，只能依靠自身的减薄来维持后续变形；二是在成形过程中，除去液压力提供的背应力，该区域还承受双拉应力，使得其接近平面应变状态，而在成形极限图（FLD）中，平面应变处于FLD 的最低点，往往是最先发生失效的位置。因此，在盒形件的拉深成形过程中，工艺参数的改变对失效位置的影响不大，即底部4 个顶点圆角处始终是失效危险区。然而，不同的工艺参数组合对失效危险区的最大减薄率有很大的影响，可通过调整工艺参数值以降低最大减薄率，从而避免失效缺陷的发生。

为了探明工艺参数对成形目标零件失效危险区最大减薄率的影响，将坯料圆角半径、压边力及液压力3个参数进行组合，结合Dynaform5.9.3进行大量有限元模拟，确定了如表3 所示单因素分析方案，为后续在响应面法中优化变量范围的确定提供依据。

2.1 坯料圆角半径对成形性能的影响

在研究坯料圆角半径对目标零件成形的影响时，保证材料参数以及其余的工艺参数一定（压边力为4MPa、液压力为7MPa），分别取坯料圆角半径为13mm、42mm、71mm、100mm、129mm、158mm 和187mm进行分析。图7 为不同坯料圆角半径下模拟所得目标零件的最大减薄率，其中压边力P为4MPa，液压力F为7MPa。当其他条件固定不变时，最大减薄率受圆角半径的影响有波动的变化规律。当圆角半径在100mm 和187mm 时，目标零件的最大减薄率比较小，但当圆角半径为187mm 时，零件完全拉深，没有法兰边，这在实际生产工艺中，存在漏液的风险，因此不考虑该圆角半径的坯料；圆角半径较小时，坯料在拉深时，由于4 个角材料的牵制作用，使得法兰圆角区材料变形很难，材料在此堆积，在拉深成形过程中，该处的材料得到周边材料的补充流动较少，只有靠自身的减薄来维持后续变形，导致最大减薄率增加；当圆角半径太大时，会引起压边力不足而在成形初期法兰外缘容易起皱，从而使得坯料在成形后期极易产生壁裂。

2.2 压边力对成形性能的影响

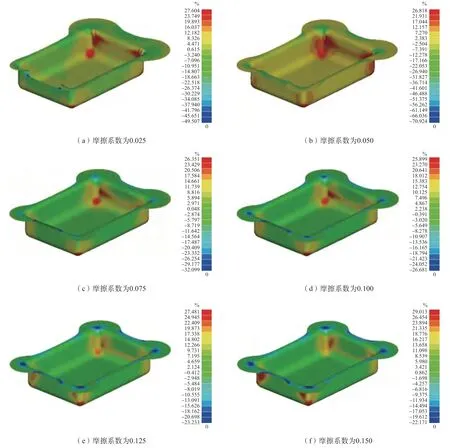
图5 不同摩擦系数下减薄率模拟结果Fig.5 Simulation results of thinning rate of part under different friction coefficients

为了研究压边力对目标零件成形的影响，同样保证材料参数以及其余的工艺参数一定（液压力为7MPa、坯料圆角半径为100mm），分别取压边力为1～15MPa 进行分析。图8 为不同压边力下模拟结果中目标零件的最大减薄率（底部4 个顶点圆角处），其中液压力F为7MPa，圆角半径R为100mm，可以看出，当其他条件固定不变时，仅仅改变压边力，目标零件的最大减薄率基本不随压边力改变而改变。这主要是因为在成形过程中，由于压边圈与模具之间的压边间隙设置为1.32mm，而坯料厚度为1.2mm。因此，在成形过程中，压边圈并未与坯料直接接触，二者之间存在0.12mm 的间隙。此时，压边力的作用主要是为了防止成形过程中坯料法兰边翘起和法兰边过度起皱，而对材料在成形过程中的流动影响较小[4，15]。故改变压边力的大小，对减薄率的影响并不显著。

2.3 液压力对成形性能的影响

为了研究液压力对目标零件成形的影响，在保证材料参数以及其余工艺参数不变的条件下（压边力为4MPa、坯料圆角半径为100mm），分别取液压力为3MPa、5MPa、7MPa、9MPa 和11MPa 进行分析。图9 为不同液压力下模拟所得目标零件的最大减薄率。可以看出，当液压力小于8MPa 时，失效危险区的最大减薄率变化不明显，而当液压力大于8MPa 后，随着液压力的增大，最大减薄率急剧增大。这主要是因为当液压力过大时，材料的应力状态发生了一定程度的改变。过大的液压力不只起到提供背应力的作用，更为重要的是，在较大的液压力作用下，材料将在厚度方向上受到压应力作用而发生一定程度的塑性变形，从而进一步加剧了材料厚度减薄。另一方面，在坯料未完全贴模之前，侧壁直段处于一定程度的悬空区，此时液压力在悬空区有一定的反胀效果。而过大的液压力将导致侧壁直段的径向拉应力增大，使得顶点圆角处的壁厚发生减薄[4]，这也致使顶点圆角处的最大减薄率急剧上升。

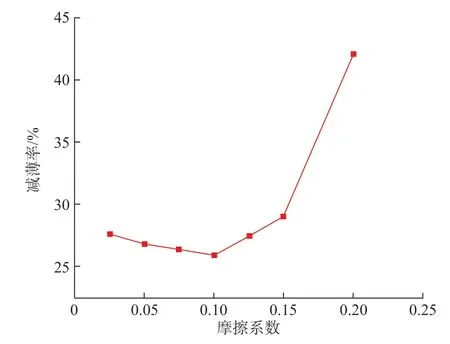
图6 不同摩擦系数下零件最大减薄率的变化趋势Fig.6 Variation trend of maximum thinning rate under different friction coefficients

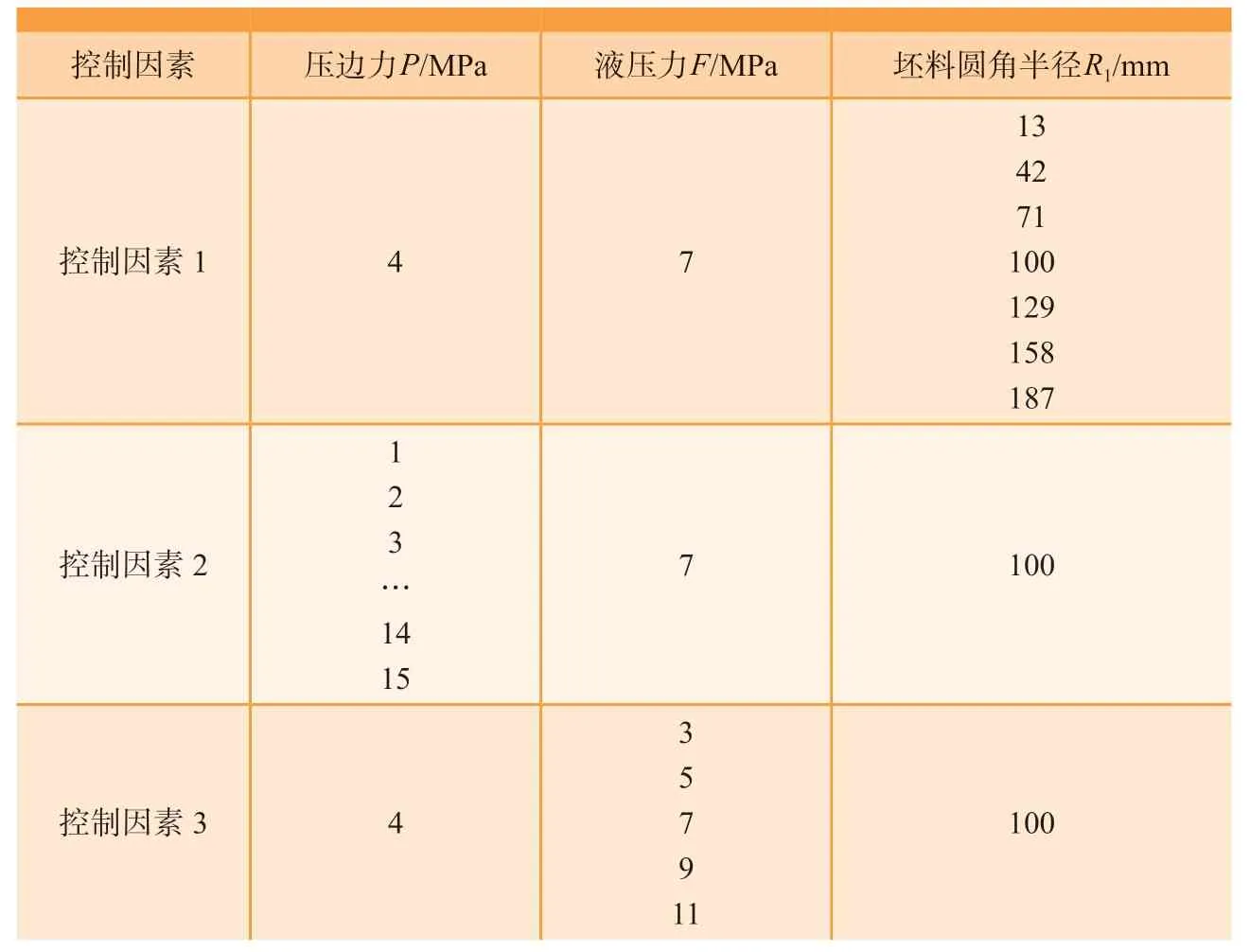
表3 单因素分析方案Table 3 Single factor analysis scheme

基于响应面法的关键工艺参数优化

由上述分析结果可知，目标零件的最大减薄率受圆角半径和液压力的影响比较大，而压边力的影响并不显著。但是工件的成形质量往往涉及多个参数间的交互作用影响，可以通过响应面法对工艺参数进行优化，获得可成形目标零件最优成形质量的工艺参数，充分发挥该工艺的潜能。

响应面法是一种通过利用回归分析对收集到的合理数据建立各响应量与工艺参数之间函数关系的统计与数学方法。常见的试验设计方法包括3k 全因子设计、中心复合设计（Central composite design, CCD）和Box-Behnken 设计，其中CCD 是最常用的一种方法，较其他设计方法具有试验次数少、模拟精度高、拟合曲面好等优点[19-21]。

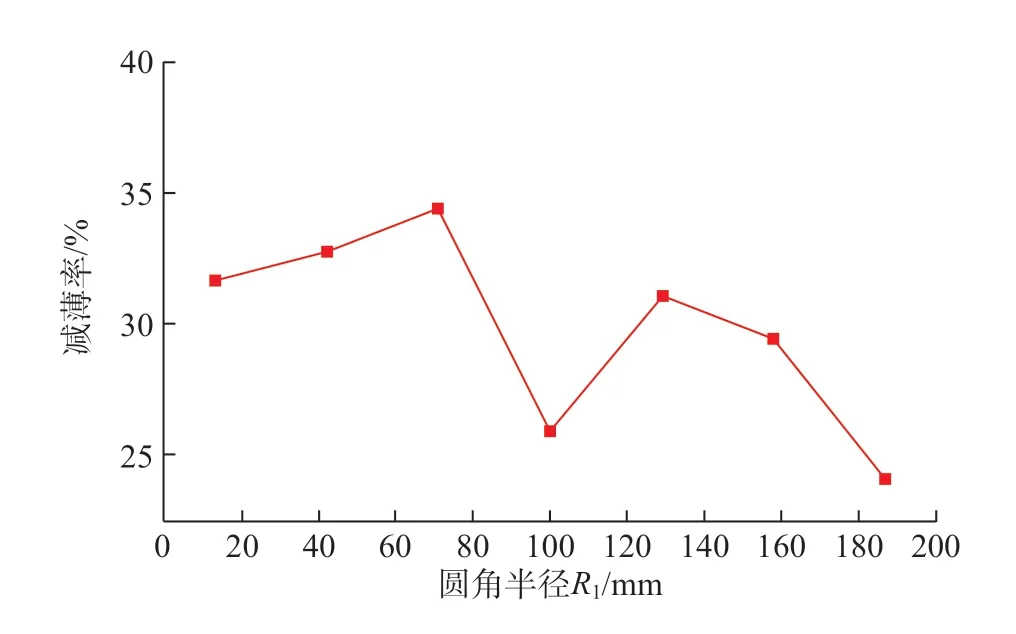
图7 不同圆角半径下最大减薄率的变化趋势Fig.7 Variation trend of maximum thinning rate under different fillet radius

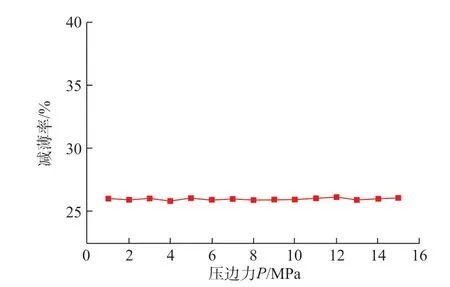
图8 不同压边力下最大减薄率的变化趋势Fig.8 Variation trend of maximum thinning rate under different blank holder forces

1 响应面模型的试验设计

根据目标零件的几何特征，以最大减薄率低于30%为目标，对坯料圆角半径、压边力和液压力3 个参数进行优化。通过响应面法可以获得响应量和优化变量之间的经验函数关系，通常使用一阶或者二阶模型能很好地描述两者之间的关系。一阶模型表达式为：

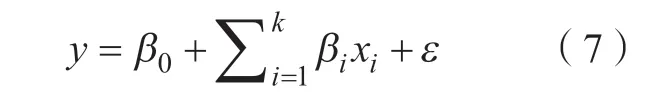
二阶模型表达式为：

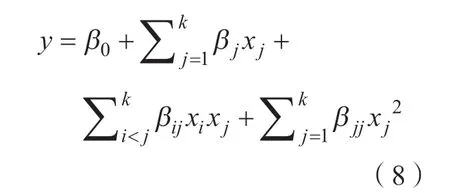
式中，y为响应量；β0为未知系数；βi、βj、βjj分别是一阶项和二阶项的系数；xi、xj为各个工艺参数；k为工艺参数的个数；ε为试验随机误差；xi xj为参数i与参数j间的交互作用；xj2为参数j的二次作用；βij为参数i与参数j之间的交互作用系数。上述一阶和二阶模型中的各系数以及常数项均可用最小二乘法进行拟合获得，获得未知参数后即得到了经验函数的表达式。通过对目标零件成形有限元模拟结果分析，确定各个参数水平值如表4 所示。由Design Expert 12 软件的中心复合设计法设计出如表5 所示的试验方案。

2 响应面模型设计及方差分析

通常使用建立模型的方差分析来表征模型的准确性和分析不同工艺参数对优化量影响的大小。多元相关系数R2表示工艺参数引起的变动占总变动的百分比，因此多元相关系数在0 到1 之间，同时多元相关系数越接近1，则模拟数据点在回归直线附近越密集，拟合效果越好[22]。多元相关系数R2的计算公式为：

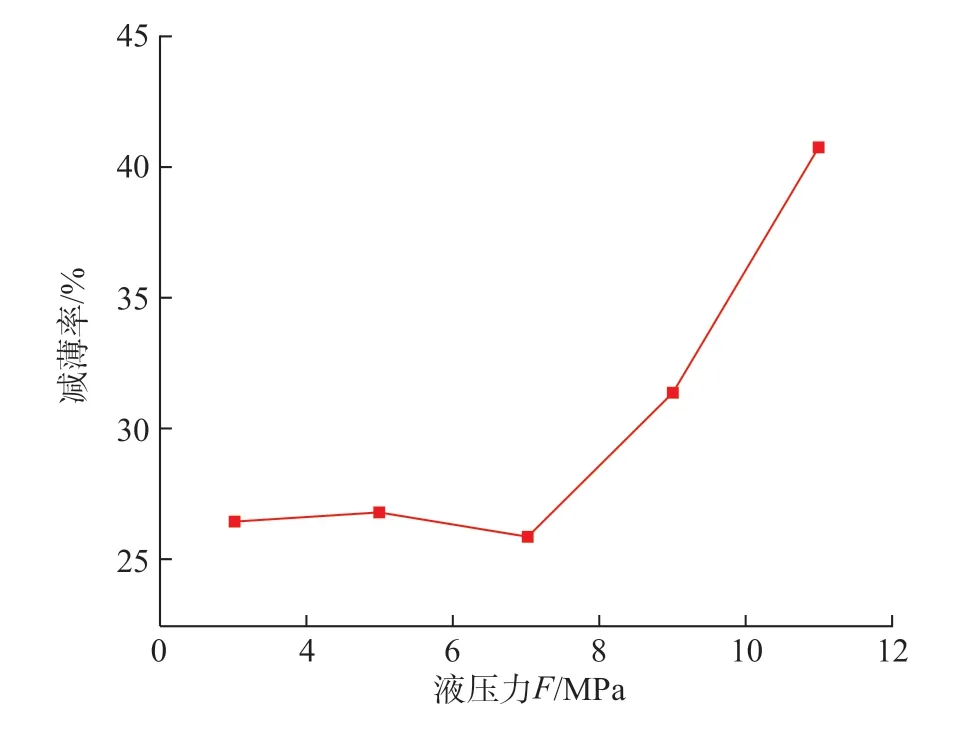
图9 不同液压力下最大减薄率的变化趋势Fig.9 Variation trend of maximum thinning rate under different hydraulic pressure

表4 工艺参数及其水平值Table 4 Process parameters and level values

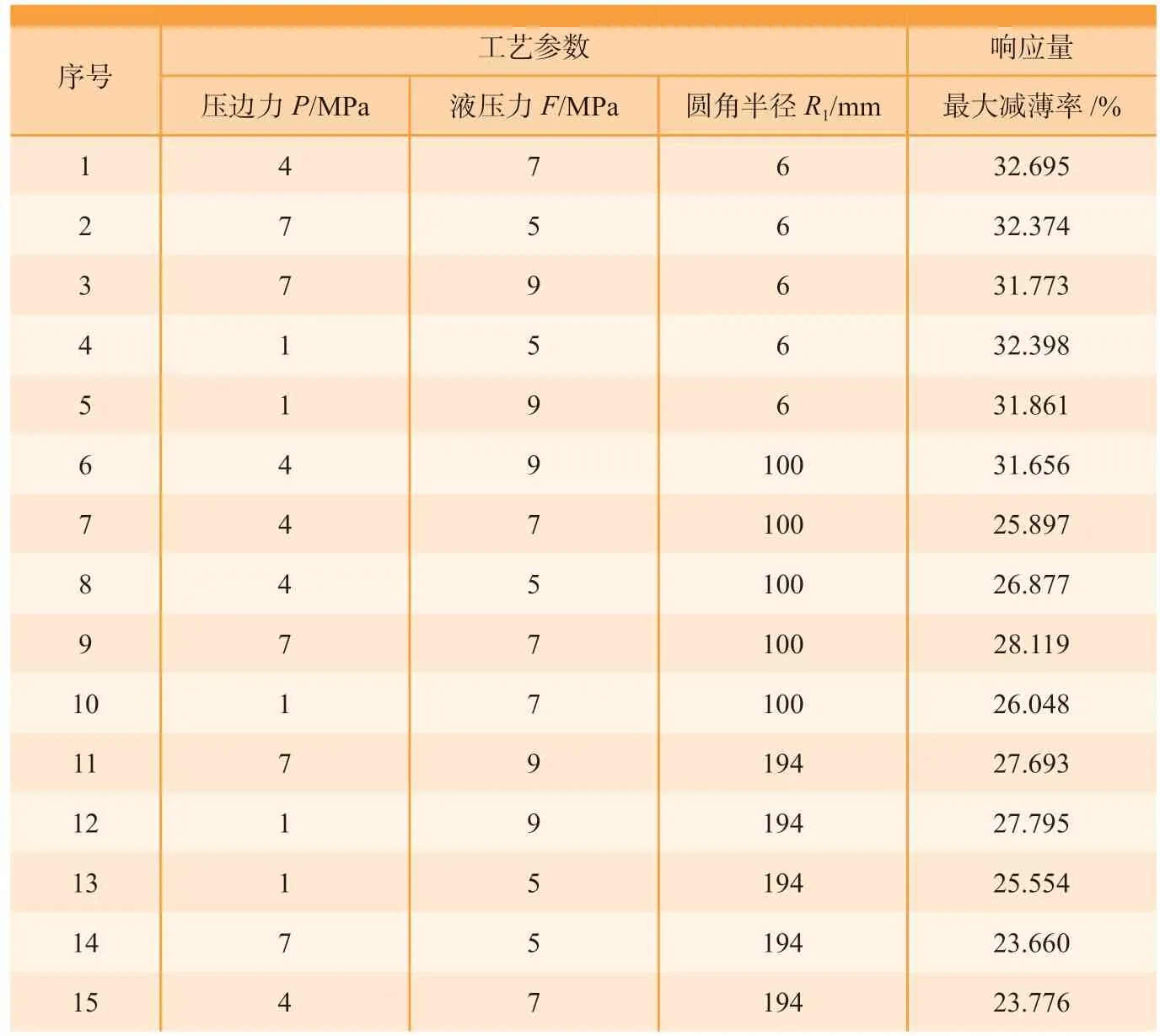
表5 响应面试验设计及有限元模拟结果Table 5 Response surface experimental design and finite element simulation results

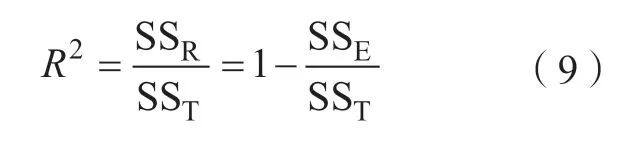
式中，SSR表示回归平方和；SSE表示残差平方和；SST表示总平方和，即SSR与SSE之和。

当变量增加时，必然会带来R2值增加，但并不是每一个因子项对响应量的影响都显著，如果只用R2值来判断模型，可靠度明显是不够的。因此使用修正的多元相关系数，其计算公式为：

式中，m′为对响应量的影响不显著的因子项数目，n为试验总组数。由此可见，如果m ′＞1，即有对响应量影响不显著的因子项存在时，R2adj＜R2。

此外需要使用F′值来衡量模型的有效性和各变量的显著性，F′值的计算公式为：

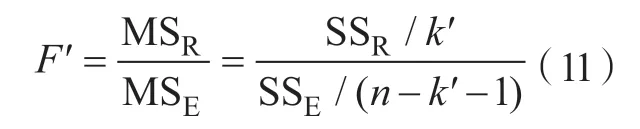
式中，MSE为残差均方；MSR为回归均方；k′为响应模型中因子项的个数。F′值越大，说明模型更加有效。一般设置某一临界值F′0，当F′＞F′0时认为该模型是有效的。在目前的各种统计软件中，常将F′＜F′0的概率用P′值代表，一般设置P′＜0.05 时表示模型或因子项是有效的[23]。

通过Design Expert 12 软件使用最小二乘法对表5 试验数据进行拟合。最大减薄率响应模型方差拟合结果如表6 所示。可以看出，模型的P′值小于0.05，表明所建立的模型是显著，但是也可以看出，与压边力x1相关的x1、x1x2、x1x3、x12模型项的P′值均大于0.05，对最大减薄率的影响并不显著，这和上文得出的结论相同。因此本研究不考虑压边力的影响，对试验数据重新进行拟合，拟合结果如表7 所示。

表7 为不考虑压边力影响的最大减薄率响应模型方差分析结果，可知模型的P′值为0.0003，小于0.05，说明模型的建立比较合理。同时多元相关系数R2的值为0.8987，修正多元相关系数的值为0.8424，均接近1，说明模型的精确度较高。在模型的其他变量中，x2、x3对响应量的影响都是显著的。表6 和表7的结果验证了上文的结果，即目标零件的最大减薄率受圆角半径和液压力的影响比较大，而压边力的影响不显著。

因此，建立的最大减薄率与工艺参数之间函数关系，仅仅考虑了液压力x2和圆角半径x3的影响，没有考虑压边力x1的影响。得到经验函数如下：

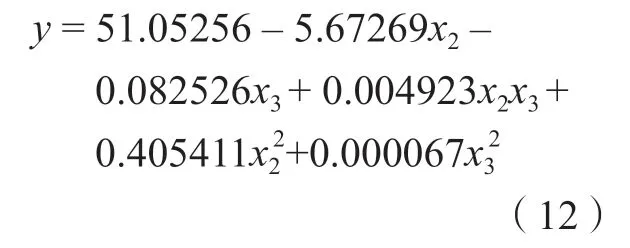
残差是指实际测量值与模型拟合预测值之间的差值。残差分析检验通过得到的差值信息，判断模型的可靠性。残差概率分布越接近同一条直线，说明实际值与预测值的差值越小，则模型的可靠性越好。图10为残差的正态概率分布图，可以看出各个残差序列点在一条直线的附近大致呈正态分布，说明模型拟合较好，试验设计具有可靠性。图11 为残差与预测值分布图，可看出响应面模型的残差序列点分布的比较分散，随机性较好。残差序列点的正态性、分散性及随机性分布表明所构建的响应面模型拟合效果好，可靠性强[24]。

表6 最大减薄率方差Table 6 Variance of maximum thinning rate

表7 不考虑压边力的最大减薄率方差Table 7 Variance of maximum thinning rate without considering BHF

图12 为最大减薄率的预测值与实际值关系图，可以看出预测值与实际值的各点大致分布在同一条直线上，说明响应模型的预测值与实际值较为接近，其误差基本可忽略不计，建立的最大减薄率二阶响应模型可以较为准确地预测成形过程中的实际值。

3 响应面分析

通过对各响应模型的三维函数图进行绘制，可直观地分析各工艺参数对响应量的交互影响规律。由单因素分析以及响应面模型分析可知，压边力对目标零件的最大减薄率影响不显著，因此绘制出液压力与圆角半径对最大减薄率交互影响的响应面图，如图13 所示。因此在保证零件完全成形的前提下，通过获得的响应面进行寻优以获得最低的最大减薄率。为了保证盒形零件的产品要求，以最大减薄率低于30%为优化目标。通过盒形零件的最大减薄率与工艺参数之间二阶响应模型使用Design Expert 12 获得了最佳工艺参数组合如下：压边力为2.819MPa，液压力为5.268MPa，圆角半径为100.24.8mm。考虑到实际成形过程中的可操作性，修正最佳工艺组合为：压边力为2.8MPa，液压力为5.3MPa，圆角半径为100mm，以修正后的最佳工艺参数进行有限元模拟，模拟结果如图14 所示。成形零件最大减薄位置也在底部圆角部位，该处的曲率半径变化比较大，和模具之间产生的接触摩擦也比较严重，材料流动性不如其他部位，导致了在拉深成形过程中，该处的材料得到周边材料的补充流动较少，只有靠自身的减薄来维持后续变形。使用响应面法优化得到的最大减薄率为25.594%，使用有限元法得到的最大减薄率为26.18%，相对误差为2.29%，验证了响应面模型的准确性。

4 响应面优化工艺的试验验证

根据修正后的最佳工艺参数进行了一道次充液拉深成形试验，得到的实际目标零件如图15 所示。为了验证模拟结果的准确性，采用超声波测厚仪，针对所成形零件的不同位置进行了壁厚测量，如图15（b）所示。考虑零件的对称性，仅测量图15（b）中1～18 号点的位置。从测量结果可以看出，最大减薄位置出现1 号、5 号、11 号等位置，这与模拟所得规律相吻合。但是减薄率在数值上存在一定偏差，模拟所得最大减薄率为26.18%，而实测最大减薄率为27.31%，二者的相对误差为4.3%（图16）。这可能与试验过程中的润滑有关系。在模拟过程中，对摩擦系数进行了理想化假设，即认为成形时摩擦系数在摩擦处均相等。而在实际成形时，往往由于模具表面的粗糙度不同、润滑剂的均匀性以及厚度不同等原因，造成摩擦系数在各处存在差异。特别是在1 号、5 号、11 号等变形较大的位置，随着变形的进行，摩擦系数会有一定程度的增大，进而造成了实际减薄率大于模拟减薄率的现象。另一方面，通过实测壁厚和模拟结果的对比可以看出，二者之间的误差较小，这也验证所建立有限元模型的准确性。同时，也证明了采用响应面法得到的回归模型有很高的可靠性。

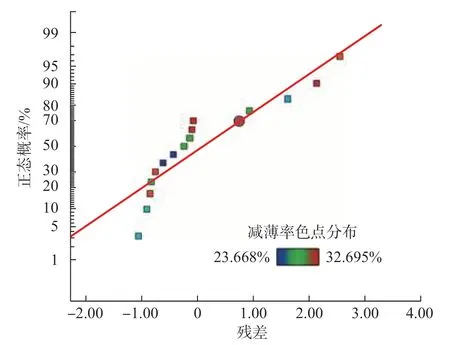
图10 模型残差的正态概率Fig.10 Normal probability distribution of model residuals

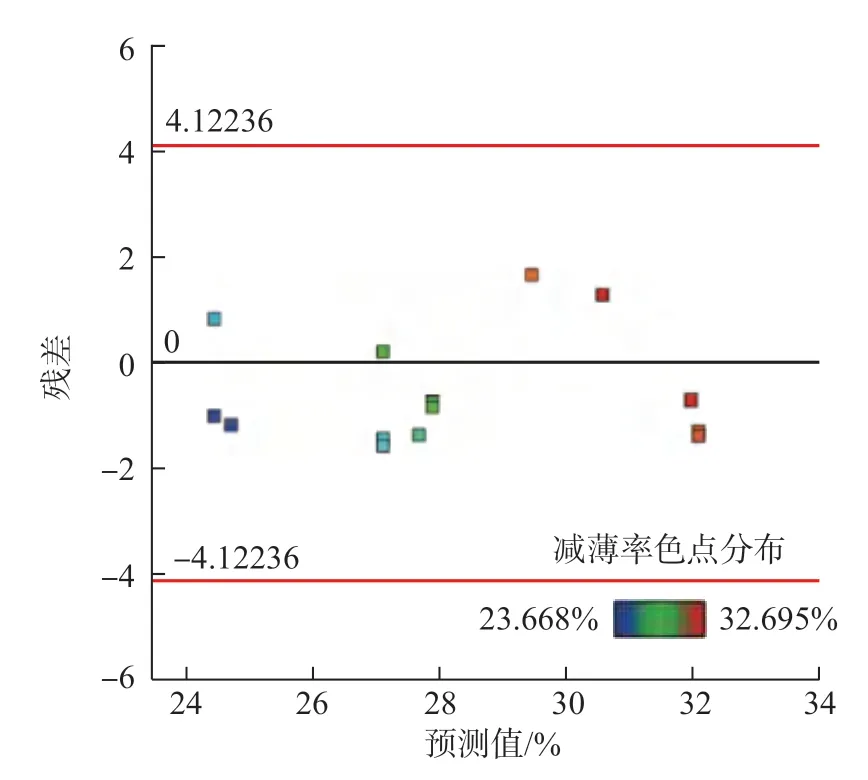
图11 残差与预测值分布Fig.11 Distribution of residuals and predicted values

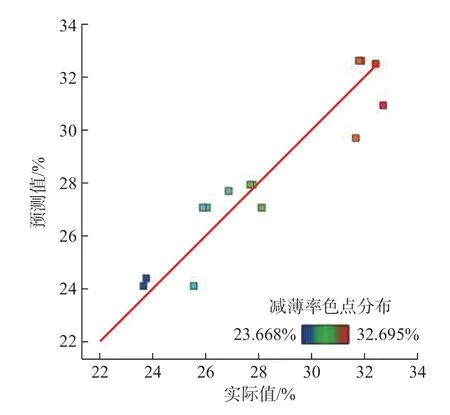
图12 最大减薄率模型的预测值与实际值Fig.12 Predicted values and actual value of maximum thinning rate model

结论

本文采用有限元模拟结合响应面法，以目标零件的最大减薄率为优化指标，对盒形零件充液拉深成形中的工艺参数进行了优化，得到的主要结论如下：

（1）目标零件的最大减薄率受液压力和坯料圆角半径的影响比较大，而压边力的影响不显著。随着液压力增大，目标零件的最大减薄率也随之增大；坯料圆角半径对最大减薄率的影响无明显的变化规律，当圆角半径在100mm 和187mm 时，目标零件的最大减薄率比较小。

（2）建立了盒形零件的最大减薄率与工艺参数之间二阶响应模型，以最大减薄率小于30%为目标优化条件，通过该二阶响应模型获得了最佳工艺参数组合为：压边力为2.8MPa，液压力为5.3MPa，圆角半径为100mm。

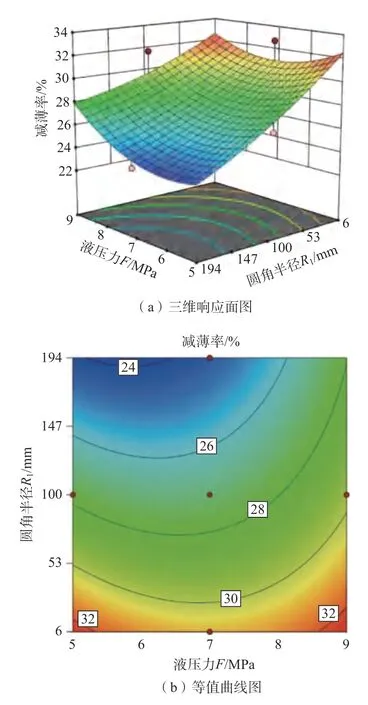
图13 液压力与圆角半径对最大减薄率交互影响的响应面图Fig.13 Response surface diagrams of interaction between hydralic pressure and fillet radius on maximum thinning rate

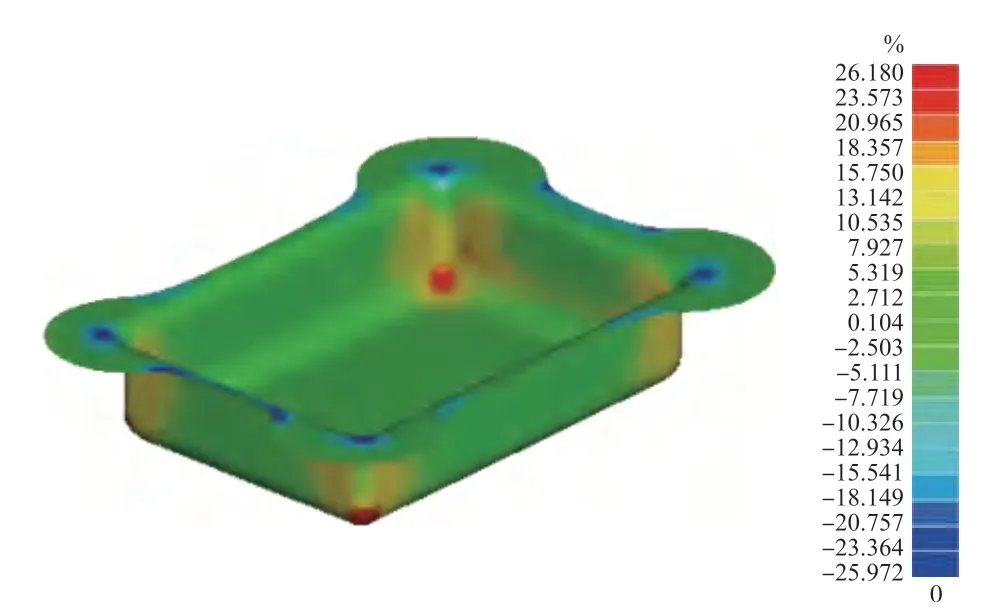
图14 工艺参数修正后有限元模拟结果Fig.14 Finite element simulation results after correction of process parameters

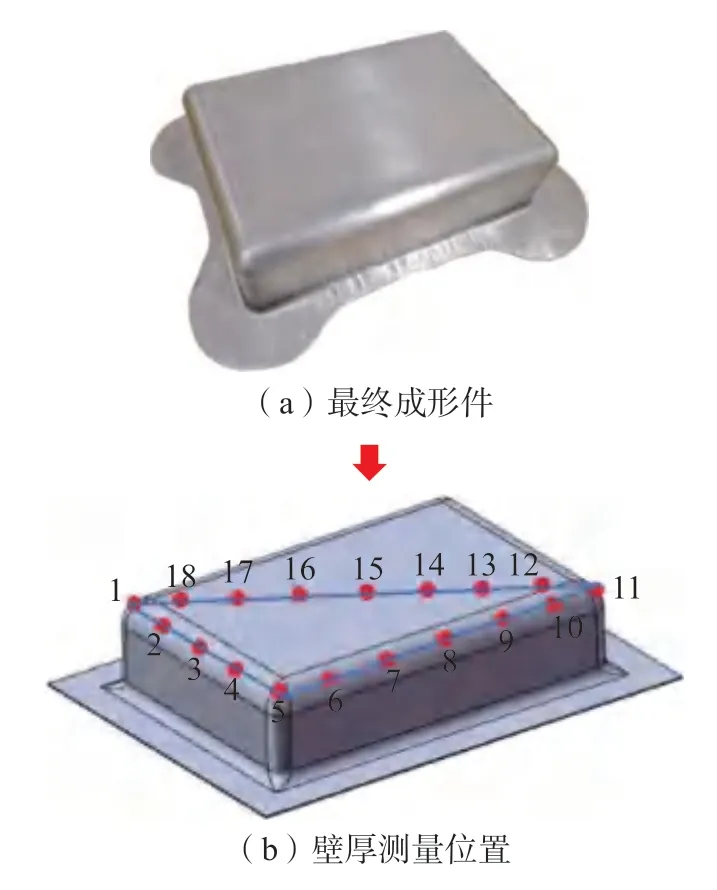
图15 目标零件Fig.15 Target part

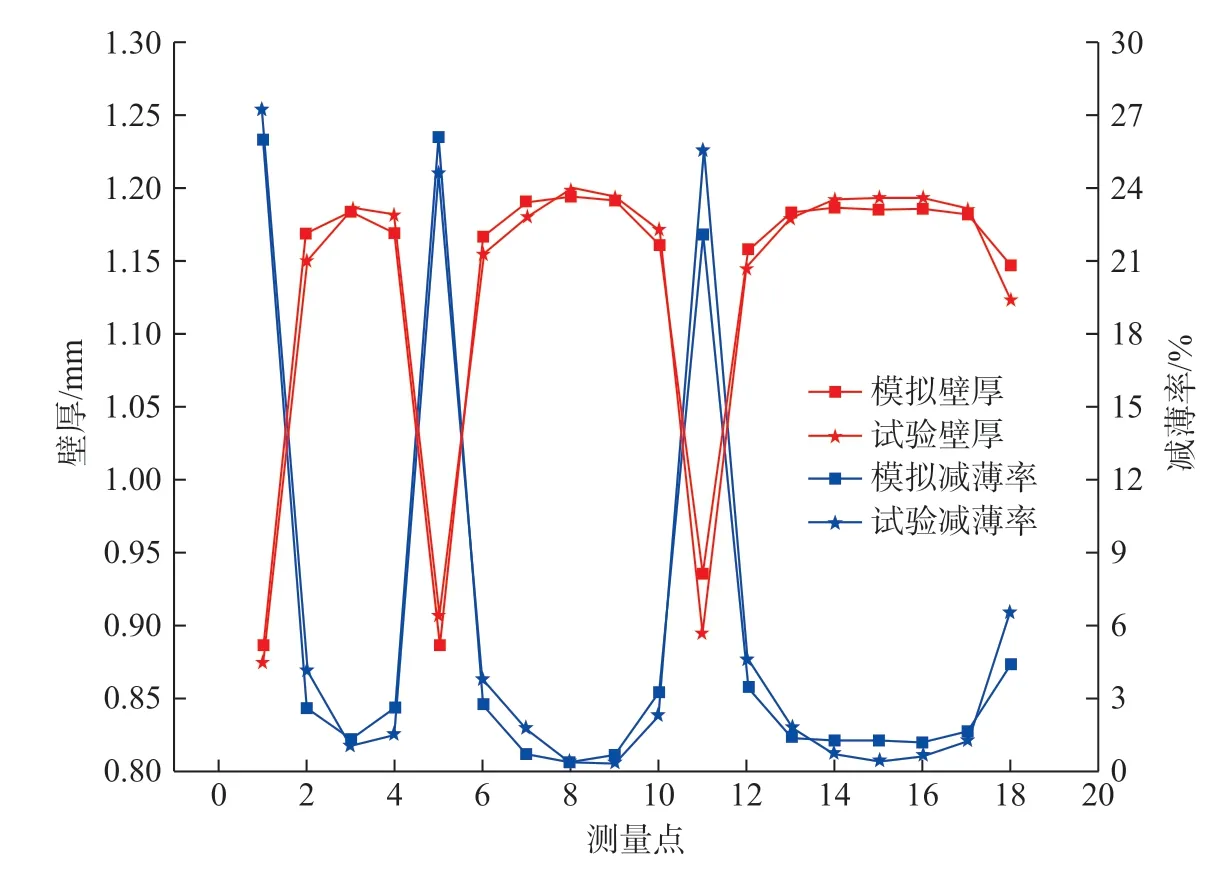
图16 壁厚与减薄率的模拟和试验结果对比Fig.16 Comparison of simulated and experimental results of wall thickness and thinning rate

（3）利用修正后的工艺参数对盒形零件进行有限元模拟，模拟结果与试验值对比，相对误差不超过5%。同时利用该最佳工艺参数组合开展一道次充液拉深成形试验，可获得满足成形质量要求的盒形零件。