混沌粒子群优化扩展卡尔曼滤波北斗伪距定位

曹学瑶， 胡黄水， 韩 博

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

北斗卫星导航系统是我国自行研制、独立运行的全球卫星导航系统。和美国的GPS、俄罗斯的“格洛纳斯”(GLO-NASS)以及欧洲的“伽利略”系统并列为全球四大卫星定位系统[1]。目前,北斗卫星导航系统已具备亚太区域导航服务能力。

伪距定位具有易于实现、速度快、不存在整周模糊度等优点，具有很大的应用价值。目前,伪距定位算法普遍采用最小二乘算法、卡尔曼滤波算法(Kalman filtering)等。在伪距定位算法中，最小二乘算法是一种相对简单且广泛的算法。但最小二乘算法在定位中无法处理数据中的粗差且计算量大，所以,利用最小二乘定位算法使得定位精度下降[2]。卡尔曼滤波算法通过预测方程和更新方程对目标进行最优状态估计[3-4]，由于观测数据中的量测噪声和系统噪声对解算存在干扰，所以卡尔曼滤波解算过程也是滤波过程。卡尔曼滤波算法在导航及高精度卫星定位领域也得到广泛应用。文献[5]提出基于卡尔曼滤波方法的BDS伪距单点定位算法，相较于最小二乘算法，卡尔曼滤波算法的定位精度有明显提高。针对卡尔曼滤波算法在状态转移、观测等非线性条件下无法保持正态性问题，文献[6-7]提出扩展卡尔曼滤波定位算法。扩展卡尔曼滤波算法使用雅克比矩阵代替卡尔曼滤波中的线性矩阵，使扩展卡尔曼滤波在非线性条件下可以保持正态性，进而提高定位精度，文献[8-9]提出粒子群优化扩展卡尔曼滤波算法，首先采用具有最小均方误差估计效果的 EKF 滤波算法，其次加入粒子群算法来优化EKF 噪声矩阵,进而提高定位精度。

但粒算子群算法(Particle Swarm Optimization, PSO)在粒子寻优过程中具有随机性，导致粒子无法收敛到全局的最佳位置且易于陷入局部极值。该缺陷使算法不能实现最优化并影响算法精度，不能满足高精度的定位要求。因此,提出混沌粒子群优化扩展卡尔曼滤波算法，在传统粒子群的基础上添加混沌扰动，扩大粒子群的应用范围，摆脱局部最优，进而提高收敛速度和定位精度。

1 伪距定位算法

伪距定位原理是通过北斗导航系统中导航卫星的三维位置坐标信息,以及卫星到接收端的距离得到用户端的三维位置坐标信息的过程。其中导航卫星的三维位置坐标信息可以通过导航电文中的星历数据获得，由于卫星发射的信号会受到各种误差的干扰,导致用户端接收到的观测距离并不准确。将带有误差的观测距离称为伪距[10]。公式如下：

ρi=ri+δρ1+δρ2+c(δtu-δt1),

(1)

(2)

式中:ri----第i颗卫星与用户端的真实距离：

ρi----卫星与用户设备之间的真实距离；

δtu----电流层的时延距离；

δρ1----对流层的时延距离；

δt1----用户设备的钟差；

δρ2----卫星的钟差；

c----信号的传播速度，c=2.997 924 58 m/s;

(xi,yi,zi)----第i颗卫星的位置坐标；

(x,y,z)----接收机的位置坐标。

忽略可修正项，伪距定位公式

ρi=ri+c(δtu-δt1)=

i=1,2,…,n,

(3)

式中：δt----接收机的钟差。

2 EKF 滤波算法

北斗导航系统的观测模型和状态模型为：

状态方程

xk=Ak,k-1xk-1+ωk-1。

(4)

观测方程

yk=Bkxk+vk,

(5)

式中：xk----历元k的系统状态向量;

xk-1----历元k-1的系统状态向量；

Ak,k-1----历元k-1 到历元k的状态转移矩阵；

yk----历元k的观测量；

Bk----状态量和观测量之间的关系矩阵；

ωk-1,vk----高斯白噪声，均值为零，且相互独立。

EKF滤波过程公式如下：

预测方程

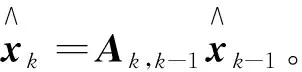
(6)

先验估计值的协方差

(7)

滤波增益矩阵

(8)

状态更新方程

(9)

协方差阵更新方程

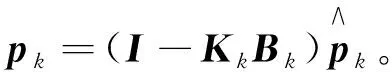
(10)

3 混沌粒子群算法

3.1 粒子群算法

粒子群算法是1995年由Eberhart和Kennedy开发的一种进化优化算法，其灵感来自对鸟群觅食行为的研究[11]。粒子群算法用一个随机的个体群体进行初始化，其中每个个体被称为具有位置和速度的粒子。当已知粒子群的初始位置和速度值时，种群中粒子的速度和位置通过式(1)和式(2)不断地迭代更改,进而找到最优解。

Vij(t+1)=ωvij(t)+c1*r1j*(Pbest(t)-

Xij(t))+c2*r2j*(Pgbest(t+1)-

Xij(t)),

Xij(t+1)=Xij(t)+Vij(t),

(11)

式中:Vij(t)----第i个粒子第j维上的速度向量；

Xij(t)----第i个粒子在第j维上的位置向量；

Pbest(t)----第i个粒子当前搜索到的最佳位置向量；

Pgbest(t)----种群中迄今为止搜索到的最佳位置向量；

t----当前时间；

c1,c2----粒子的加速度系数；

r1j,r2j----两个独立均匀分布的随机变量，目的是给迭代计算加入随机性，范围为[0，1]；

ω----进行自适应变化的惯性权重，表示粒子上一时刻速度对下一时刻运动的影响。

(12)

式中：ωmin----初始权重;

ωmax----最终权重;

Tmax----最大迭代数;

t----当前迭代数。

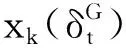
(13)

N----迭代次数；

PSO算法的运算过程如图1所示。

图1 PSO算法流程图

3.2 混沌粒子群

针对传统粒子群算法在迭代过程中易过早陷入局部极值点收敛的缺点，提出混沌粒子群算法[13-14]，目的是增加粒子变异，扩大算法的迭代范围，能够保证粒子可以收敛到全局的最佳位置，减少局部最优解的存在[15]。混沌理论是科学家在1975年提出的[16]，在电路系统、保密通信及工程研究领域都得到了广泛应用。在混沌粒子群中，粒子具有随机性和遍历性，不会重复经历空间内全部状态。混沌粒子群算法克服了粒子陷入局部极值的弱点，提高了优化算法效率，得到了最佳优化结果。

混沌点列的生成过程：

1)假设粒子m维位置向量

xi=(xi1,xi2,…,xim)。

映射向量

yi=(yi1,yi2,…,yim),

其中

式中：ak----xik的上界；

bk----xik的下界。

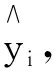
混沌粒子群算法的执行过程如下：

1)设置卡尔曼滤波算法的状态变量和噪声协方差的初始值；

2)初始化种群中粒子的位置和速度；

3)通过式(13)得到粒子适应度，确定每个粒子的极值和全局极值；

4)通过式(11)的迭代计算更新粒子的当前位置和速度进行寻优；

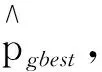
7)更新粒子最优值和全局最优值，满足终止条件，则输出混沌粒子群算法的最优解,即最优解R、Q。

3.3 混沌粒子群优化 EKF 结构

基于混沌粒子群优化EKF 结构如图 2 所示。

图2 混沌粒子群优化的 EKF 结构

图中:R----系统协方差阵；

Q----系统测量噪声协方差阵；

xk----输入值;

zk----测量值。

通过各时刻的目标函数值和滤波参数值,以及混沌粒子群算法对系统噪声R和测量噪声Q寻找最优解，将优化后的系统噪声和测量噪声代入扩展卡尔曼滤波后的运算过程，再通过式(6)～式(10)可以算出k时刻的最优估计滤波值xk。

4 仿 真

文中定位解算中使用的是CGCS2000坐标系，对 RINEX文件数据进行解算。分别采用粒子群优化EKF算法和混沌粒子群优化EKF算法对X、Y、Z三个方向进行定位解算，然后再将定位结果进行对比分析。

误差对比如图3所示。

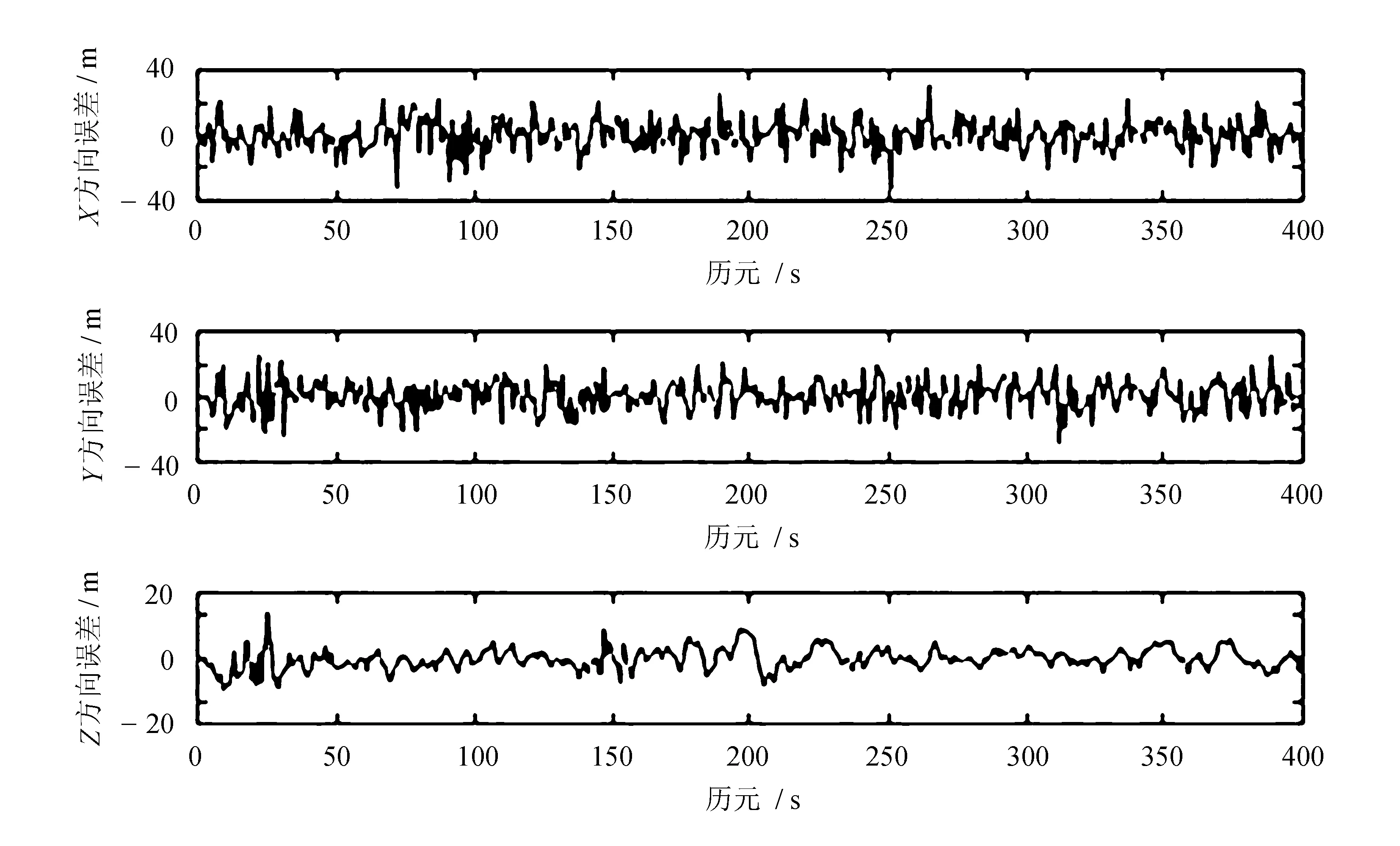
(a) 粒子群优化扩展卡尔曼滤波算法

(b) 混沌粒子群优化扩展卡尔曼滤波算法图3 X、Y、Z三个方向的误差结果对比

图3明显可以看出,混沌粒子群优化扩展卡尔曼滤波算法的定位误差更小，滤波结果也更加平滑。混沌粒子群优化扩展卡尔曼滤波算法的定位解算结果相较于传统粒子群优化扩展卡尔曼滤波的定位精度有明显提高，相较于图3(a)的收敛过程也明显缩短，实现了更加精确的定位。

粒子群优化EKF和混沌粒子群优化EKF三个方向的误差对比结果见表1。

表1 误差对比 m

表1可以看出，混沌粒子群优化EKF算法的定位精度较传统粒子群优化EKF算法提高约70%，滤波结果也更加平滑。故混沌粒子群优化EKF算法极好地改进了定位误差。

5 结 语

提出混沌粒子群优化扩展卡尔曼滤波定位解算算法，利用混沌粒子群优化扩展卡尔曼滤波算法的系统噪声和测量噪声来抑制滤波发散情况,进而提高定位精度。在混沌特性的作用下，粒子算法搜索的遍历性得到完善。不再局限于几个局部的最优值，而是产生更多的局部最优邻域点，由此对粒子去除局部极值起到关键作用，进而提高精度,保证效率和时效性。

通过 Matlab处理数据的实验结果表明,混沌粒子群优化EKF算法的收敛速度与定位精度均明显提高。