基于自适应Lasso的缺失数据图模型选择

郑倩贞， 徐平峰

(长春工业大学 数学与统计学院， 吉林 长春 130012)

0 引 言

在高斯图模型中，协方差逆阵可解释随机变量间的条件独立性。矩阵中的零元素表示对应两个随机变量间条件独立，因此,协方差逆阵中零元素的估计问题是图模型选择中的关键问题。惩罚似然方法可同时实现模型选择和参数估计，其中Lasso惩罚是常用的求解稀疏估计的惩罚项，例如：Yuan M等[1]、Banerjee O等[2]、Friedman J等[3]、Stidler N等[4]、徐平峰等[5]都采用l1惩罚对数似然方法估计协方差逆阵,从而得到稀疏的图结构。文献[5]基于gCoda方法将成分数据的图模型选择问题转换为高斯图模型的协方差逆阵估计问题；文献[4]研究的是数据存在随机缺失时的高斯图模型选择问题；而其余三者关注的均是数据完全观测下的高斯图模型选择问题，但三者采用的优化算法不同。

研究表明，Lasso惩罚可得到稀疏估计，但其估计结果会产生偏差[6]。Fan J等[6]提出的SCAD惩罚和Zou H[7]提出的自适应Lasso惩罚都能够降低估计的偏差。Fan J等[8]将这两种惩罚应用于完全数据的图模型选择问题以减弱协方差逆阵估计的偏差。但在实际高维复杂数据中，往往存在数据部分缺失的情况。针对数据完全随机缺失情形，文中将采用自适应Lasso惩罚对数似然方法对高斯图模型选择进行研究，并与Stidler N等[1]的l1惩罚对数似然方法(MissGLasso)进行比较。

1 自适应MissGLasso

设x=(xobs,xmis)为来自多元高斯分布Np(μ,Ω-1)的n个独立同分布样本。令样本中的观测数据xobs=(xobs,1,…,xobs,n)，缺失数据xmis=(xmis,1,…,xmis,n)，其中xobs,i和xmis,i分别表示第i个样本的观测数据和缺失数据的集合，i=1,2,…,n。与文献[4]相同，文中假设数据的缺失机制为可忽略的。基于观测数据xobs，可给出观测对数似然函数

l(μ,Ω;xobs)=

((Ω-1)obs,i)-1×(xobs,i-μobs,i))，

(1)

式中：μobs,i----第i个样本中观测变量的均值;

(Ω-1)obs,i----第i个样本中观测变量的协方差阵。

在惩罚似然的框架下，下述优化问题的解可作为均值μ和协方差逆阵Ω的估计，

(2)

式中：λ----正则化参数;

ωjk----Ω中的(j,k)元素;

p(·)----定义在各元素ωjk上的惩罚函数，j,k=1,2,…,p。

若令惩罚函数p(|ωjk|)=|ωjk|，则可得到Lasso惩罚，那么由上式求得的解即为MissGLasso估计[4]。

(3)

我们称该估计为自适应MissGLasso(AdaMissGLasso)。针对上述优化问题，可结合EM算法[9]和GLasso算法[3]进行优化求解。

2 EM算法

EM算法常用于处理缺失数据下的参数估计问题，该算法通过迭代交替进行E(期望)步和M(最大化)步，直至算法收敛。E步是在给定观测数据和当前参数的情况下，计算完全数据的对数似然函数的条件期望；M步是关于待估参数极大化E步中的完全似然条件期望。令第t次迭代的估计值(μ(t),Ω(t))作为当前参数，其中(μ(0),Ω(0))代表EM算法的初始值，设为均值插补后的GLasso估计。第(t+1)次迭代如下:

1)E步。

给定观测数据xobs和当前参数(μ(t),Ω(t))，计算完全数据惩罚对数似然函数的条件期望，记为Q函数。为简单起见，记E(·|xobs,μ(t),Ω(t))为Et(·)。于是，Q函数可表示为

Q(μ,Ω|μ(t),Ω(t))=

(4)

其中

与Fan J等[8]相同，文中取γ=0.5。

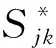
(5)

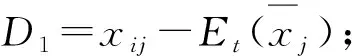
因此，E步只需计算Et(xij)和Et(xijxik)。

对第i个样本xi=(xobs,i,xmis,i)，μ和Ω可分块表示为:

给定观测数据xobs,i和当前参数(μ(t),Ω(t))，xmis,i的条件分布为N(ci,σi)，其中

于是，可推得[4,10-11]

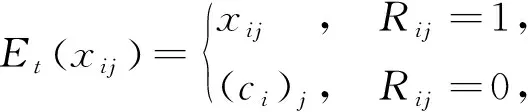
(6)

以及

式中：Rij=1----xij为观测数据；

Rij=0----xij缺失，i=1,2,…,n，j,k=1,2,…,p。

2)M步。

M步通过最小化Q(μ,Ω|μ(t),Ω(t))来更新参数估计(μ(t+1),Ω(t+1))，

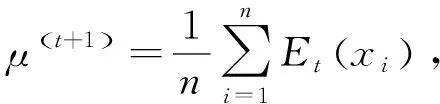
(8)

式(8)中Ω(t+1)的优化问题可直接由GLasso算法求解。将(μ(t+1),Ω(t+1))作为下一次迭代的当前参数，重复E步和M步直至算法收敛。

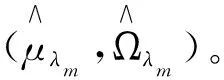
m=1,2,…,k，

(9)

其中

3 模拟研究

在完全随机缺失的机制下，文中对自适应MissGLasso方法和MissGLasso方法在高斯图模型上的参数估计和模型选择进行了模拟比较。现考虑以下两个模型：

1)AR(1)，(Ω-1)jk=0.7|j-k|。

2)Ω=B+δI，其中B的对角线元素为0，非对角线元素之间相互独立，取值为 0.5或0，且P(Bjk=0.5)=0.1。选择恰当的δ，使得Ω的条件数为p。

对于以上两个模型，设定随机变量个数p=100,200,300，对两个模型与随机变量个数p的6种组合，均产生样本量n=200的50个独立的数据集，且在每个数据集上完全随机删除10%、20%、30%的数据。因此，每个完全观测的数据集对应3个具有不同缺失比例的缺失数据集。为评价算法性能，文中比较以下指标。

Kullback-Leibler损失(kl)、真阳率(tpr)、阳性预测率(ppv)以及马修斯相关系数(mcc)。

式中:Ω----真实的协方差逆阵;

tp----真阳类的个数;

tn----真阴类的个数;

fp----假阳类的个数;

fn----假阴类的个数。

基于模型1和模型2的不同参数设定各评价指标的均值和标准差分别见表1和表2。

表1 不同参数设定下模型1各评价指标的均值和(标准差)

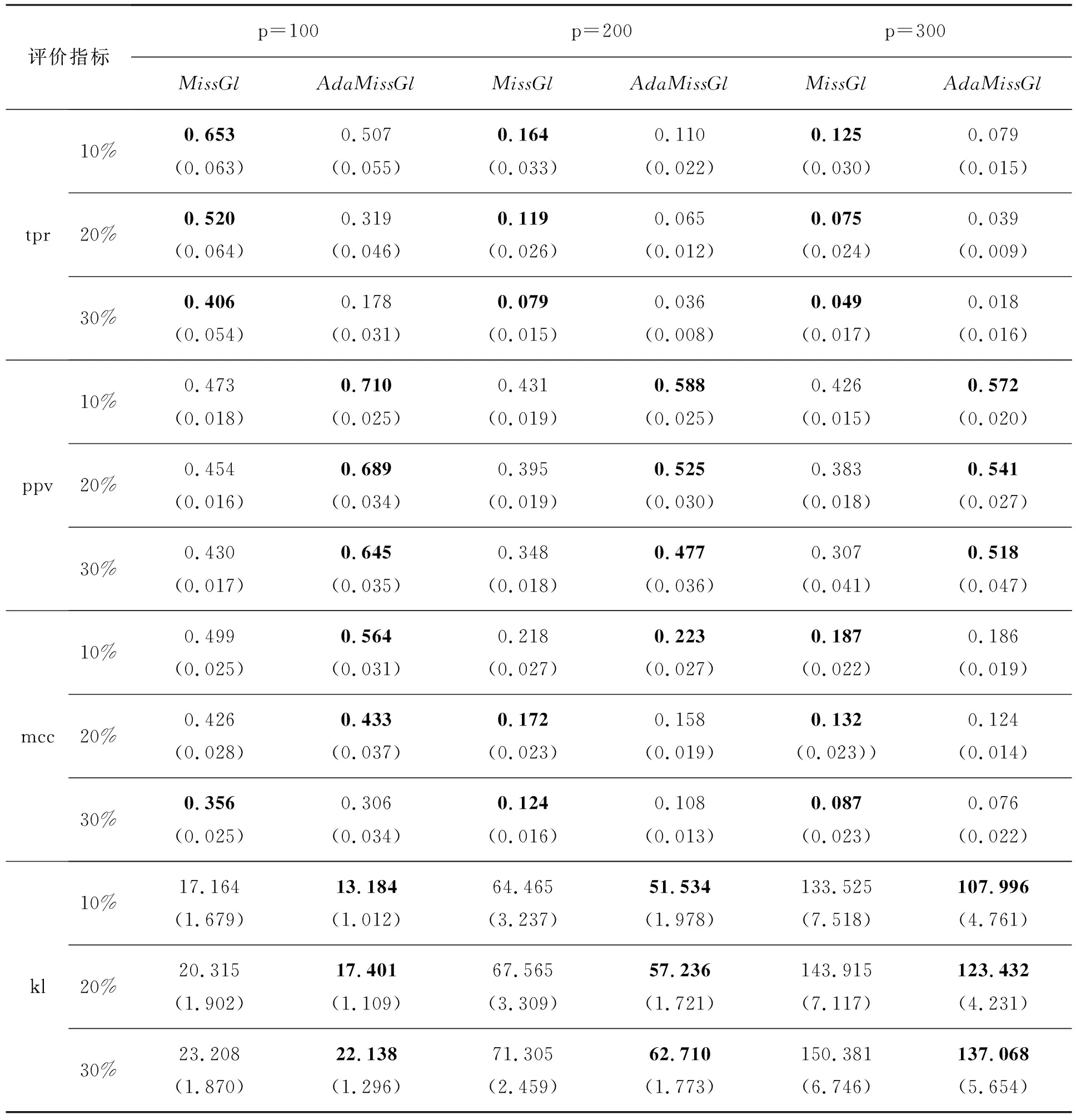
表2 不同参数设定下模型2各评价指标的均值和(标准差)

由表中可以看出，对于模型1和模型2的所有设定，除了tpr以外，自适应MissGLasso方法均优于MissGLasso，并且模型1的tpr仅在缺失比例为30%时略低。对于模型2，自适应MissGLasso方法的mcc略低，但是两者相差不大。kl为评价协方差逆阵估计效果的指标，不论模型1还是模型2，自适应MissGLasso的估计性能都更佳。综上所述，自适应的方法更优。

4 实例分析

基于自适应MissGLasso方法，文中对枯草芽孢杆菌生产核黄素(维生素B2)的数据集进行了图模型分析。该数据集由DSM(瑞士)提供，可在文献[12]的补充材料中下载。数据为完全观测，包含71个样本，4 088个协变量以及1个响应变量。协变量为4 088个基因表达水平的对数；响应变量为核黄素生产率的对数。为简单展现自适应MissGLasso方法的图模型选择效果，文中仅对经验方差最大的100个基因，以及测量核黄素生产率的响应变量作图模型推断，即数据集riboflavinv100.csv[12]。该数据集样本量n=71，随机变量个数p=101。

不同缺失程度下重叠边数的箱线图如图1所示。

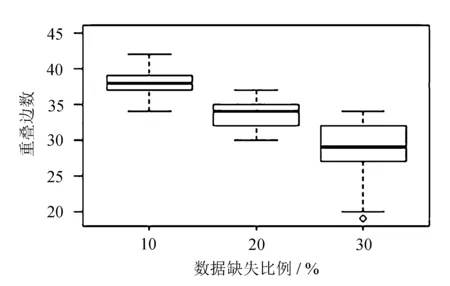
图1 不同缺失比例下的重叠边数

从图1中可以看出，数据缺失的比例越高，重叠的边数越少。即使数据集中缺失30%的数据，自适应MissGLasso方法仍能识别出约30条重叠的边。

不同缺失比例下的平均稀疏矩阵如图2所示。

由图2可以看出，该矩阵的(j,k)元素为50次模拟中协方差逆阵估计值(j,k)元素的非零频率。

图2说明缺失比例越高,选出的边越少，图模型越稀疏。

图2 不同缺失比例下的平均稀疏矩阵

5 结 语

基于惩罚似然框架提出自适应MissGLasso方法以处理缺失数据情形下协方差逆阵的估计问题，采用EM算法和GLasso算法进行优化求解。该方法可用于数据完全随机缺失的情况。通过不同模型下的模拟实验结果显示，自适应MissGLasso方法的图模型选择性能及协方差估计结果较MissGLasso方法更优。此外，对核黄素生产数据集的图模型结构学习实验同样验证了自适应MissGLasso方法具有良好的模型选择性能。