基于离线标定的快速图像拼接算法

于国栋， 王春阳， 兰孝野， 徐鹏宇， 张 月， 刘晓辰， 李忠琦

(中国人民解放军63869部队，吉林 白城 137001)

1 引 言

对于一些大视场、大场景，特别是近些年比较热门的360°全视场监控等应用，由于单个摄像机的视场和功能限制，通常难以够覆盖完整的角度。一般对大视场范围的图像采集或者全景视频监控有两种解决方式，一种是使用广角摄像头；另一种是使用多台固定的摄像机覆盖完整的监控范围，然后再经过图像拼接获取完整的监控区域[1]。但是由于受相机功能和价格的限制，广角摄像机往往难以被采用。为此，需要寻找一种在大视角拍摄情况下，能快速获取高质量画质的图像采集技术。

图像拼接是将在同一时间和地点拍摄的几张具有一定重合区域的照片拼接成一张全景图像的技术，是计算机视觉和图形学领域的研究课题之一。全景图像拼接技术广泛应用于安防监控、战场态势感知、虚拟现实技术和医学图像等多种领域[1-2]。传统图像拼接过程一般包含图像预处理、图像配准、图像映射和图像融合等几个步骤[3]。

传统的图像拼接算法是基于输入的每一帧图像进行特征提取和计算配准的拼接方法。具体步骤是先提取特征点，然后再进行特征匹配与融合等步骤。但是对于实时的图像拼接场景，传统方法需要消耗大量的空间和时间，因此若是对每一帧图像都进行特征提取和匹配，无法满足实时拼接的要求，容易出现鬼影等问题。泊松图像融合算法，虽然融合效果较好，但计算量较大。此外还有基于最佳缝合线和相关的改进算法，但是都无法满足实时拼接的要求。传统的图像融合算法中，基于多分率的图像融合算法是在RGB三个通道上做拉普拉斯金字塔并实现融合，计算量大。

本文提出了一种基于YUV色彩空间的拉普拉斯金字塔的快速图像融合算法，解决适用于多摄像头合成全景视频拼接难题。系统由多台安放在固定位置的相机组成，具有固定的重合面积，并且使用相同的外部触发，对实时采集到的图像进行拼接。考虑到实际应用场景中相机的角度、位置和重叠的区域固定，所以采用离线标定，在离线标定阶段就计算出相机的映射关系，然后保存到本地。在每次拼接时加载映射矩阵，无需再重复进行特征提取和匹配，可以省去拼接过程中大量的前期工作，直接进入图像拼接、融合步骤。

2 离线标定

2.1 SIFT特征匹配

离线标定的第一阶段是对待拼接的图像进行特征提取和配准。常用的特征提取算法中,基于尺度不变的有SIFT算法[4]和SURF等算法[5-6]，这些算法各有优缺点。由于在实际应用中使用离线标定方法，所以无需关注在离线标定阶段中特征提取和全局配准所消耗的时间，因此选用效果最好的SIFT算法[7]。

假设Ri和Sk是一对配准点的SFIT描述符，SIFT特征向量为128维，即包含128个数据[8]，其中Ri=(ri1,ri2,…,ri128)，Sk=(sk1,sk2,…,sk128)，则Ri和Sk的欧氏距离计算公式如下：

(1)

2.2 单应性矩阵计算

在摄像机数学模型中，一个三维空间中的点P=[X,Y,Z,1]T映射到摄像机二维平面上的点p=[x,y,1]T满足以下关系：

p=MP，

(2)

假设两个摄像机的相机映射矩阵分别为M1和M2，T通过这两个相机拍摄的图像中有相同点P，而点P在两幅图像中的齐次坐标分别为p1和p2，则有下列公式成立：

(3)

(4)

这样，摄像机中相应点的变换就可以用一个3×3的单应性矩阵H表示。两幅图像之间的单应性矩阵H可以表示成如下形式：

(5)

H为非奇异矩阵，因此对于点p1、p2用非齐次坐标代替齐次坐标，设p1和p2的非齐次坐标为p1=[x1,y1,1]T和p2=[x2,y2,1]T，则二维投影变换的关系可表示为：

(6)

(7)

由于一对匹配点只能确定2个线性方程，因此理论上需要至少4对匹配点才可以求出投影变换矩阵H。对于实际工程中有n个点对(n>4)时，最终可利用最小二乘法计算出投影变换矩阵M。

3 快速图像融合算法

3.1 传统的的拉普拉斯金字塔图像融合算法

图像融合是将图像配准之后的待拼接图像在空间上进行叠加。图像融合直接影响拼接后图像的质量。传统的图像融合算法，例如加权平均融合计算量小，可用于快速图像拼接，但融合效果较差，容易出现鬼影等问题[8-12]。泊松图像融合算法虽然融合效果较好，但计算量较大。此外还有基于最佳缝合线和相关的改进算法，但是都无法满足实时拼接的要求。传统的图像融合算法中，基于多分率的图像融合算法是在RGB三个通道上做拉普拉斯金字塔并实现融合，计算量大。

本文采用一种改进的多分率图像融合方法，提出在YUV色彩空间中进行拉普拉斯金字塔图像融合。该方法可以减少大量的计算，并且图像融合效果较佳。

(1)首先构造高斯金字塔，将原始图像作为金字塔的最底层图像G0，使用高斯卷积核对图像进行卷积，然后再下采样得到上一层图像G1。重复进行卷积核下采样操作i次即可获取第i层图像Gi，迭代多次，即可形成图像高斯金字塔。

Gi+1=DOWN(Gi+1⊗g3×3)，

(8)

其中g3×3是高斯卷积核。DOWN表示下采样计算。

(2)构造拉普拉斯金字塔，在构建高斯金字塔的过程中，持续的卷积核下采样会造成图像高频信息的丢失，所以使用拉普拉斯金字塔来保存图像的高频信息。将上一层的高斯金字塔图像进行上采样后再进行卷积操作，使用该层的高斯金字塔图像减去卷积后的图像即可得到当前层的拉普拉斯金字塔图像。

拉普拉斯金字塔中第i层图像：

Li=Gi-UP(Gi+1)⊗g3×3，

(9)

其中:Li是拉普拉斯金字塔中第i层的图像，Gi是高斯金字塔中第i层的图像，UP表示上采样计算。

(3)融合后恢复图像，处理的过程需要对每一层金字塔融合。处理的过程从上到下，最终获得原始图像。

完成每一层的图像融合之后，要根据融合后的拉普拉斯金字塔重构高斯金字塔，并最终得到实际融合后的图像，计算公式如下：

Gi=Li+DOWN(Gi+1)⊗g3×3.

(10)

3.2 改进的拉普拉斯金字塔图像融合算法

(1)色彩空间转换

RGB和YUV色彩空间的互相转换公式如下：

(11)

(12)

(2)处理Y通道

在YUV色彩空间中，Y通道表示像素点的亮度信息并反映图像中灰度值的动态范围。YUV色彩空间将亮度和颜色分开，Y部分指标是融合后图像的亮度信息，UV通道表示颜色信息。在图像融合中，高对比度的区域应给更高的权重，所以拉普拉斯金字塔可以很好地保留高对比度的区域。

拉普拉斯图像融合，其实就是权重融合，本文从两个方面考虑权重、对比度因子和颜色深度因子。

对比度因子公式如下：

C(i,j)k=|Yk(i+1,j)+Yk(i-1,j)+Yk(i,j+1)+Yk(i,j-1)-4Y(i,j)|，

(13)

其中：Yk(i,j)是第k层中坐标为(i,j)的Y通道值。

颜色深度因子Ek(i,j)公式如下：

Ek(i,j)=|Uk(i,j)×Vk(i,j)+ε|，

(14)

其中：Uk(i,j)和Vk(i,j)分别表示第i层输入图像在坐标(i,j)(i,j)处的U通道和V通道的值，ε是一个很小的值，避免权重为0。

最终的实际权重为：

Wk(i,j)=Ck(i,j)×Ek(i,j)，

(15)

使用这个权重来完成图像融合，最终可得到融合后的Y通道图像。

(3)处理UV通道

(16)

(17)

根据上述公式获取融合后UV通道的值，即相同像素点位置，选择两个中较大值的U和V。最后将融合后的YUV色彩空间图像转换为RGB色彩空间的图像即可。

4 实验验证

为验证文章方法的有效性，在场区生活区选取一个宽阔场地验证实际拼图效果。本文选用的图像获取设备为华为Mate20，该手机内置镜头为徕卡三摄镜头，采用“广角+超广角+5倍长焦距”的组合。其中，广角镜头1 200万像素(f/1.8光圈，等效焦距27 mm)，超广角1 600万像素(f/2.2光圈，等效焦距17 mm)，长焦镜头800万像素(f/2.4光圈，等效焦距52 mm)。程序运行环境Visual Studio，算法实现工具OpenCV4.1.0,操作系统是Windows10,CPU配置为Corei7-8750,2.20GHz。

在拍摄场景前，随机选取两个拍摄位置，相距大约5 m，拍摄图像并保存。

图像处理分两个阶段：离线标定阶段和实时拼接阶段。这两个阶段的主要任务和工作如下：

(1)离线标定阶段

离线标定阶段主要包括特征提取、特征匹配和单应性矩阵的计算。

离线标定阶段的任务是提取特征点和进行特征匹配，最终根据匹配的结果计算出单应性矩阵。该矩阵在实时拼图时加载，直接用于图像映射，可节省大量的特征提取和配准时间。

(2)实时拼接阶段

实时拼接阶段包括加载单应性矩阵计算和图像融合。

图1 待拼接图像Fig.1 Diagram of images to be spliced

图1为待拼接的两张图像，分别取全景图像的左右两部分，经特征匹配和校准后，得到配准的特征点。如图2所示，绿色圆圈表示SIFT特征提取和配准后得到的特征点。使用这些配准的特征点计算得到透视变换矩阵为：

(18)

图2 SIFT算法特征配准结果Fig.2 Result of SIFT algorithm feature registration

新建两张空图L和R，高度与原图相等，宽度是原图的两倍，将待拼接的左图拷贝到图L中 待拼接的右图经单应性矩阵计算后投影到图R中，得到对齐后的图像，如图3所示。图4为加权平均融合算法得到的结果，从拼接效果可以看出，使用SIFT特征提取和配准之后的特征点计算得到的单应性矩阵可以使图像获得较好的对齐效果。

图3 图像对齐Fig.3 Diagram of image alignment

图4 加权平均融合算法Fig.4 Diagram of weighted average fusion algorithm

虽然使用该单应性矩阵有较好的图像对齐效果，但是也存在一定的缺点，经过矩阵运算对齐后的图像，其右侧相对于原图缺少了一部分。产生这种情况的主要原因为：右侧的点经过单应性矩阵计算后其坐标超出目标图像矩阵的范围，导致超出范围的这部分被抛弃了。在实际应用中，如果图像侧边不重要，可以忽略。但如果侧边图像有必要保留，可通过修改单应性矩阵的方式保留该部分图像信息。

单应性矩阵公式如下：

(19)

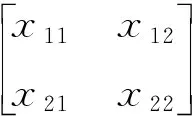
图像对齐后，分别采用加权平均算法、改进的渐入渐出算法、传统拉普拉斯金字塔融合算法和本文算法，对图像进行融合处理，其效果如图4～7所示。相对于使用加权平均融合算法，无论是传统的拉普拉斯图像融合还是本文算法都有更好的融合效果。加权平均融合算法和改进的渐入渐出算法在一些细微之处无法将两幅图像中的同一个物体融为一体，而是当作两个物体同时保留在图像上，融合效果较差，而拉普拉斯算法却可以识别并做了很好的融合。

使用3个不同大小的融合区域(320×1 440，430×1 440，730×1 440)进行多次融合取处理时长的平均值，比较3种算法的融合速度。如表1所示，加权平均融合算法虽然有较快的处理速度，但是融合效果不佳。改进的渐入渐出图像融合方法相对于加权平均融合算法图像拼接效果更好，但是也会带来更复杂的计算。传统拉普拉斯算法和本文算法处理效果几乎一致，但是处理效率差别较大，本文算法的处理时间明显快于传统拉普拉斯金字塔融合算法，处理时间提高了近3倍。

图5 改进渐入渐出图像融合算法Fig.5 Diagram of improved gradual in gradual out image

图6 RGB色彩空间拉普拉斯融合Fig.6 Diagram of Laplace fusion in RGB color space

图7 YUV色彩空间拉普拉斯融合Fig.7 Diagram of Laplacian fusion in YUV color space

可见，相比于传统拉普拉斯金字塔融合算法，本文方法在不降低处理质量的前提下，处理速度更快，效率更高，处理海量高清图像时，更能体现本文算法的优越性。

表1 本文算法与传统拉普拉斯金字塔融合算法处理速度对比结果Tab.1 Results of speed comparison between the two algorithms (s)

5 结 论

快速图像拼接中采用离线标定的方法可节省大量计算时间。在传统拉普拉斯金字塔图像融合基础上，提出基于YUV色彩空间的拉普拉斯金字塔图像融合，将图像亮度和颜色分离，只对Y通道做拉普拉斯金字塔图像融合，相对传统拉普拉斯图像融合速度提升了近3倍，简化了实现过程，也同样可以获取较好的图像融合效果。