多元随机过程的剩余寿命预测

冯媛媛，杨玉桃，朱向洪

(南昌大学理学院，江西 南昌 330031)

现代工业产品和设备可靠性分析及剩余寿命预测工作已经贯穿系统设计、生产、使用和维护各个阶段，对于系统正常使用和健康管理具有重要意义。如今工程系统可靠性通常较高，应用传统基于故障数据的方法存在一定的困难；而在系统使用过程中，通常会伴随着一个或者多个性能指标的退化，退化数据的获取相对简单且成本较低，因此基于退化数据的方法研究越来越多。

现有的研究工作大多数考虑一维退化数据。目前常用的方法包括基于退化轨迹、随机过程和非参数模型。王美男等[1]利用粒子滤波方法对设备退化模型的参数进行更新,通过建立与传统方法不同的粒子滤波量测方程,使依赖于更新后的退化模型参数的预测曲线符合已知退化趋势,得到更加准确的寿命预测结果。除了退化轨迹模型外，有学者尝试用非参数模型的方法来预测系统剩余寿命。康守强等[2]提出一种基于无监督深度模型迁移的滚动轴承剩余使用寿命预测方法。该方法首先对滚动轴承数据提取均方根特征，引入时间序列分割算法对振动信号进行状态信息标记，并在神经网络训练得到状态识别模型的基础上，利用状态概率估计法结合状态识别模型建立滚动轴承寿命预测模型。与退化轨迹模型和非参数模型相比，基于随机过程的剩余寿命受到了很多学者的青睐。一个重要的原因就是随机过程模型能够很好地描述退化过程随时间的不确定性。而在这个方面，目前的研究也大部分只考虑了一维退化情况。李月锌等[3]对电池容量退化服从非线性维纳过程建立状态空间模型,并认为参数是服从共轭分布的随机变量,增加了模型不确定性使之更加符合锂离子电池容量的退化过程。利用自助法和粒子滤波对每一时刻的参数及退化状态进行估计和更新,进而预测电池的剩余寿命。黄亮等[4]考虑了发动机性能退化非线性的特点,并采用多阶段Wiener过程建立发动机的性能退化模型。根据发动机的历史性能监测数据,利用极大似然估计和贝叶斯方法对参数进行评估更新，进而得到个体发动机剩余寿命的实时预测值。

以上研究虽从各个方面考虑复杂系统的实际剩余寿命情况，但其仅仅只关注一维性能指标对于系统退化过程的影响，而这种潜在假设在某些情况下不现实。如为了不同的目的(即照明和颜色)，一个发光二极管系统可能会经历不止一个降解过程[5]；在铷电灯工作时，其性能退化指标应综合考虑铷的消耗和灯的强度降低[6]。在上述情况下，若仅关注一元性能指标对系统的影响，将对进一步的系统剩余寿命预测造成巨大的偏差。从而为了更加全面地反映系统的退化状态并准确地预测其剩余寿命，往往需要同时利用多个性能指标。经以上现象启发，本文将构造一种新权重融合方法，综合考虑多个非平稳伽马过程，并采用马尔科夫蒙特卡洛方法在线更新模型参数，得出系统剩余寿命概率密度函数。另外通过裂纹实验验证所提模型的有效性并得出部分结论。

1 模型假设

基于系统性能退化数据，构建合理的退化过程模型是进行系统剩余寿命预测的基础。在描述性能指标退化过程中，由于随机过程描述变量在时间轴上不确定性的优点和Gamma过程连续非减的良好性质，所以本文选用非平稳伽马过程描述性能指标退化过程。

现假定存在m个系统且收集了每个系统中l个性能指标在正常工作时间ni内的退化数据，其中Xik(tj) 表示第i系统第k个性能指标在tj时刻的退化量。

假设1第i个系统在退化过程中，第k个性能指标Xik服从非平稳伽马过程，既而其性能指标随着时间的变化，其增量可表示为：

Xik(tj+c)-Xik(tj)～Ga(ηk(tj+c;θk),βk)

其中，ηk(t;θk)是关于时间的非减函数的形状参数，且Δηk(tj+c;θk)=ηk(tj+c;θk)-ηk(tj;θk)；βk是服从伽马过程Ga(δk,γk)的尺度参数，用来描述系统中指标间的差异。

假设2若第i个系统中，任意一个性能指标Xik超过了其对应的失效阈值Dik，则认定该系统失效。

假设3规定第i个系统的失效阈值Di由其各个性能指标所对应的失效阈值Dik综合表示，即Di=wi1Di1+…+wilDil。其中Dik、wik(k=1,2,…,l)分别表示第i个系统中第k个性能指标对应的失效阈值和权重。

假设4在采集系统的各个性能指标时，同个系统的数据采集时间必须相同，而对于不同系统而言，数据采集时间则不限定。

2 一元性能指标剩余寿命

在工程数据中,通过多个性能指标退化数据共同描述一个复杂系统的实际退化过程,并利用首达的概念对系统进行剩余寿命预测。因此，有必要在进行系统剩余寿命预测之前对一元性能指标的剩余寿命进行研究。

假设th+c表示Xk(th+c)退化过程首次达到失效阈值Dk的时间，另在本节中规定

xk=Xk(th+c)-Xk(th)～Ga(Δηk(th+c;θk),βk),从而第k个性能指标的剩余寿命可重新定义为

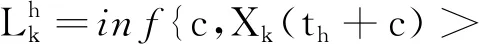
根据伽马过程的性质可知，产品退化过程中其各个性能指标到达失效阈值的首达时间th+c的概率分布函数：

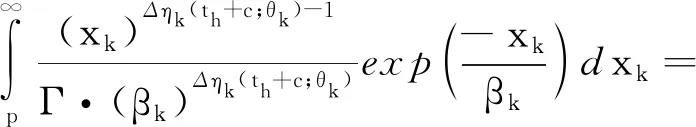
(1)

为了数值求解方便，Padget等[7]提出了利用疲劳损伤分布(BS)近似th+c的CDF。现定义Zk(t)=ηk(t,θk)且Yk(Zk)=Xk(t)，从而Yk(Zk)服平稳伽马过程且其失效时间分布可近似为：

(2)

(3)

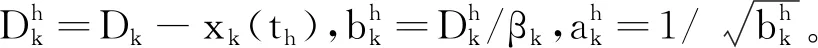
在给定X1:h的情况下，概率密度函数中尺度参数βk的更新过程是f(βk|X1:h)。利用全概率公式可得：

3 权重

系统的实际退化情况是综合考虑了各个性能指标的结果，所以各个性能指标间的关系研究就显得十分必要。而不同性能指标在描述系统实际退化情况中的占比不同，就需要权重来衡量每个性能指标对系统的重要程度。本文在两两一致性指标概念基础上提出了一种新权重计算方法(即第i个系统的第p个性能指标的权重wip)，其构造过程如下。

1) 隶属度函数。

(4)

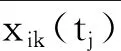
2) 构造权重wip。

本小节将在两两一致性指标的基础上构建权重wip。首先利用隶属度函数计算得出每个性能指标对应退化量，并利用文献[8]中计算方法求出第i个系统中第p维性能指标分别与其他维度的性能指标间的一致性指标。其次分别将一致性指标除以其对应维度性能指标退化数据的平均值，可得第p维性能指标和其他维性能指标的一致性程度。最后用1减去第p维的累加一致性程度,即两两不一致性指标作为权重wip。其构造方程如下：

其中，l表示性能指标的总维数，Sμ(μip,μiq)=sup min{μip(xip(tj)),μiq(xiq(tj))}是第i个系统中第p个和第q个性能变量的一致性指标[8]。之后对rik进行归一化处理:

(5)

4 产品剩余寿命

在假设3的基础上，利用权重计算方法融合多维性能指标可得出目标产品退化过程到达失效阈值D的首达时间th+ζ分布函数：

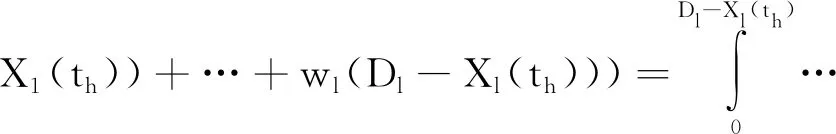
(6)

从式(6)卷积计算可以看出，融合多个性能指标作为系统总体退化指标再计算产品剩余寿命，由于公式的复杂性，计算的难度和复杂程度将非常大。进而本文将简化产品剩余寿命计算：综合式(3)所得的各个性能指标剩余寿命密度函数作为系统的剩余寿命密度函数，即：

(7)

在给定X1:h的情况下，概率密度函数中的尺度参数βk的更新过程是f(βk|X1:h)。利用全概率公式可得：

5 参数评估

由于已有的性能指标数据能对参数产生影响,所以在确定产品剩余寿命之前需利用已有数据更新参数。现假设目标系统th时仍可正常工作且可测得在th前的所有性能指标,令Xk,1:h=(xk(t1)…xk(th))'。表示目标系统的第k个性能指标在th之前的退化量。在给定目标系统X1:h=(x1,1:h,x2,1:h,…,xl,1:h)'的情况下，根据贝叶斯理论可得在th时的参数后分布。

(8)

其中ΔXk(tj)=Xk(tj)-Xk(tj-1)，同样地，在测得目标系统在th+1时的性能退化数据后，由式(8)可以实现实时的更新尺度参数(β1,…,βl)。

本节将采用两阶段方式对参数进行估计，步骤如下：

第1阶段估计参数Θ1=(θ1,…,θl),Θ2=(β11,…,βm1),Θ3=(β12,…,βm2),…,Θl+1=(β1l,…,βml)。

对于第i个系统，(θ1,βi1,…,θl,βil)完全似然函数可表示为：

(9)

其中ψ(.)表示双伽马函数，为Γ(.)算法的导函数。

6 实例验证

以裂纹增长数据为例，对上述模型和方法进行有效性验证。假设系统存在两个裂纹增长点，为了便于分析，将裂纹长度作为系统性能指标(P1和P2)。退化数据来源于文献[9]，其中包括21个裂纹增长实验数据序列，测量间隔为0.01百万转，测量终止时间为0.09百万转。

为便于验证分析，选取20个数据序列作为实验系统退化数据，并将其平均分为两组，分别作为两个性能指标的退化数据。此外，两个性能指标的初始退化量为2.286 cm，相应的故障阈值设为(P1=4.064,P2=3.302)。其具体的退化情况如图1所示。

时间/百分次

表1 参数估计

为了验证模型的有效性，模拟了基于以上的参数估计的目标系统的一元预测和二元预测，从而得出所提多元预测方法优于一元预测的结论。现已知目标系统的性能指标退化情况如图2。

在得到目标系统的退化数据后，根据上文所提出的权重计算方法分别算出P1和P2得出表2。

表2 权重及调节参数

从图2中可知当P1超过对应的失效阈值1.6时，对应的时间为0.097 1百万转(时间间隔为0.01百万转)，在本文中用t1:9={0.01,0.02,…,0.09}来验证模型的正确性。

本文利用最大误差Δ=(|xreal-xpre|)评判标准，用以比较两种预测方式的优劣性(见图3)。由目标系统数据计算可得一元预测的最大误差分别为P1=0.140 1、P2=0.262 6。二元综合预测的最大误差为0.061 5。从而可以得出本文所提出的综合多元性能指标的方法更具优势。

时间/百分次

(a) β1在0.08百万转时的采样情况

应用多元变量模型建立其目标系统的剩余寿命方程，并得出了系统在9个时间点的RL估计值，如图5所示，其中虚线表示实际系统剩余寿命，实线表示模型评估的剩余寿命。

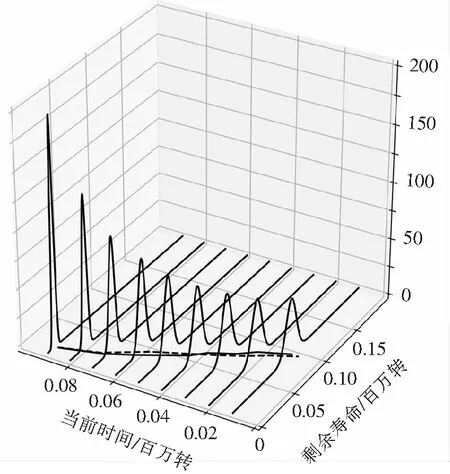
图5 剩余寿命的概率密度函数

从图(6)可知随着时间的推移，剩余寿命的相对误差越小(即使用的退化数据越多，相对误差就越小)。因此为了获得准确的估计，有必要在获得新的退化数据后重新估计结果。

7 结论

1) 相较于一元退化变量进行剩余寿命预测，多变量预测方法能够更为有效地估计系统剩余寿命；

2) 能够准确地在线预测系统的剩余寿命，并且随着退化数据累积，系统剩余寿命估计更为精确，降低维修成本提高维修效率。