基于压缩感知和位平面多重置乱的图像加密算法

刘杨曦，张烨

(南昌大学电子信息工程系，江西 南昌 330031)

图像加密是指将原始图像的信息有效地加密和隐藏，且能够在几乎无失真的情况下从加密图像中将原始图像信息还原出来。在某些特殊领域，例如商业、军事、医疗等领域，图像数据必须采用加密技术处理后，再进行传输或者存储。因此，安全可靠的图像加密算法一直是该领域的研究热点。

目前，图像加密算法通常包含置乱和扩散两个阶段。置乱主要是将明文图像中像素点的位置随机置乱，改变相邻像素值之间的相关性。文献[1]利用多重哈希函数、2D-Logistic映射和循环移位函数对明文图像像素点的位置随机置乱实现图像加密。文献[2]采用3个不同的混沌映射生成不同的拉丁方阵将彩色图像中不同分量中的像素点位置的行和列重新排列。文献[3]采用四维混沌映射生成的随机序列对图像像素点的位置重新排列，实现图像的加密。文献[4]指出数字图像在不同层次的位平面所包含的信息量不同，采用像素值与位平面值位置置乱的算法实现图像加密。文献[5]对图像所有位平面中像素点的位置做行列变换置乱，实现图像像素点位置的扰乱。文献[6]先将图像的位平面矩阵分块，利用Logistic和Chebyshev组合映射生成的随机序列对分块后的位平面矩阵重新排列，可以快速地改变图像像素点的位置，实现图像的加密。文献[7]利用六维混沌映射生成的随机序列来控制明文图像的位平面矩阵在每轮旋转过程中子矩阵的大小、方向和角度，利用明文图像的位平面矩阵的旋转，实现图像信息的加密。

扩散主要是改变明文图像中像素值的大小来实现图像的加密。文献[8]利用四维忆阻混沌系统生成的随机矩阵与明文图像分别做前向和反向两轮异或运算，将单个像素值的变化扩展到整幅图像中，实现对明文图像的加密。文献[9]采用改进的Henon映射生成随机矩阵，利用该随机矩阵对分块后的图像做异或运算，改变图像的像素值的大小来实现图像的加密。文献[10]考虑到图像中高四位的位平面含有较大的信息量，利用Logistic映射生成随机矩阵，将随机矩阵与图像中高四位的位平面值做位异或运算，简单快速地修改图像的像素值，实现图像的加密。

近年来，压缩感知技术在图像加密中也得到了广泛的应用。文献[11]将Logistic映射生成的随机序列转换成测量矩阵，再对图像的稀疏变换做压缩采样来实现图像的加密。文献[12]是在文献[11]的基础上对多图像做压缩采样，并将多个压缩后的测量值矩阵组合成一幅加密的图像。文献[13]将Logistic映射生成的随机序列作为构造测量矩阵的种子序列，生成循环测量矩阵后对明文图像做分块压缩采样。文献[14]采用由Logistic映射、Cosine映射和Tent映射组成的复合分阶混沌映射生成Bernoulli测量矩阵，利用该测量矩阵对图像做压缩采样。文献[15]将Logistic映射、Cosine映射和Tent映射组合成一种新的一维混沌映射，采用该混沌映射生成的随机序列作为种子序列生成非相干旋转混沌测量矩阵，利用该测量矩阵对明文图像做压缩采样。上述的图像压缩采样加密算法都是利用混沌系统直接生成随机测量矩阵，通常，所得到的测量矩阵的行之间具有一定的相关性，不利于解密图像的重构。

本文采用二维Logistic-Sine映射和Logistic-Sine映射生成随机矩阵，将随机矩阵经过Sigmoid非线性函数生成测量矩阵，来降低测量矩阵的行之间的相关性。再利用该测量矩阵对图像的DCT变换做压缩采样，得到测量值矩阵，也称为压缩加密图像。将压缩加密图像采用不同的切割重组方式得到比特矩阵，再对比特矩阵多重置乱，得到置乱图像。再对置乱图像做扩散运算，实现图像的加密。实验分析表明采用本文算法得到的测量矩阵在解密图像的重构过程中可以减少图像失真，具有较好的峰值信噪比和结构相似度，本文的加密算法也具有较好的加密性能。

1 相关知识

1.1 混沌系统理论

在本文提出的加密算法中，主要采用了以下3种混沌映射。

1.1.1 Logistic-Sine映射

一维Logistic-Sine映射(LSM)的数学表达式如下[16]：

xi+1=(μxi(1-xi)+(4-μ)(sin(πxi)/4))mod1

(1)

式中：μ为系数参数，μ∈(0,4)；xi为初始值，xi∈(0,1)。

1.1.2 二维Logistic-Sine映射

二维Logistic-Sine映射(2D-LASM)的数学表达式为[17]：

(2)

式中:μ、β为系统参数，μ∈(0,4),β=3，(xi,yi)为初始值；(xi,yi)∈(0,1)。

1.1.3 二维Logistic-ICMIC映射

二维Logistic-ICMIC映射(2D-LICM)的数学表达式为[18]：

(3)

式中:a、θ为系统参数，a∈(0.5,1.969),θ∈(0.721,1.4)；(xi,yi)为初始值，(xi,yi)∈(-1,1)。

1.2 位平面分解和重组

通常一幅大小为N×N、灰度级在0～255之间的灰度图像P，其像素值可以用1组8位二进制数来表示，共有8个位平面，即：Pz，z=1,2,…,8[19]。为实现位平面置乱，本文采用两种不同的位平面切割重组方式。

方式1将位平面图Pz的奇、偶数位平面重组得到两个大小为N×4N的比特矩阵，即：S1,1=[P1,P3,P5,P7]，S1,2=[P2,P4,P6,P8]。

1.3 压缩感知理论

压缩感知是指利用信号的稀疏特性，对信号压缩采样，即：

y=Φx

(4)

式中:x∈RN×1为源信号向量，Φ∈RM×N为测量矩阵，其中，M≪N；y∈RM×1为测量值向量。如x不具备稀疏特性，可以利用正交基Ψ=[Ψ1,Ψ2,…,ΨN]∈RN×N，对信号x做稀疏表示，即：

(5)

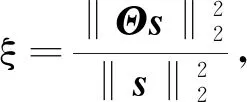
式中:s=[s1,s2,…,sN]T∈RN×1为信号x的系数向量，通常要求向量s中最多有K个非零元素，且K≪N，则s为信号x的稀疏表示，则式(4)可写为：

y=Φx=ΦΨs=Θs

(6)

式中:Θ=ΦΨ为传感矩阵。为了从y中重构信号s，矩阵Θ应满足有限等距性质(restricted isometry property,RIP)，即：

(7)

若0≤δ<1，则传感矩阵Θ满足RIP性质。

2 加密算法

本文的加密算法主要分成4个部分：混沌系统的初始值及其随机序列的生成、压缩采样加密、位平面置乱加密和扩散加密。图1为本文的图像加密算法流程图，具体加密过程如下。

图1 提出的加密算法流程图

2.1 混沌系统的初始值及其随机序列的生成

利用原始图像P，采用SHA-256哈希函数得到长度为256的二进制哈希值H，将哈希值H分成32组，每组由8个二进制数组成，即：

(8)

(9)

式中:xw为混沌系统的初始值，w=0,1,…,5。

将(x0,x1)作为2D-LASM系统的初始值，迭代N0+N/2次后舍弃前N0个值，得到两个长度为N/2的随机序列c1和c2，其中，N0为随机常数。再将(x4,x5)作为2D-LICM系统的初始值，迭代N0+MN次后舍弃前N0个值，得到两个长度为MN的随机序列d1和d2。通常，M=r×N，r<1为压缩比。

2.2 压缩采样加密

(10)

再将矩阵O中的每一个元素经过非线性函数后得到随机矩阵L对应的每一个元素，即：

(11)

式中:u=1,2,…,M/2，v=1,2,…,N/2。再对矩阵L列规范化，得到测量矩阵Φ，即：

(12)

式中:M′=M/2。

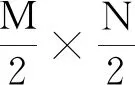
Yl=ΦP2,l

(13)

将测量值矩阵Yl按照图像P的行和列切割的逆过程，组合得到大小为M×N的矩阵Y。对Y规则化，使其取值范围在[0,255]内，即：

(14)

式中:Ymin为矩阵Y中的最小值；Ymax为矩阵Y中的最大值；P3为压缩加密的图像。

2.3 位平面置乱加密

采用1.2.2节中的方式1，将P3重组得到两个大小为M×4N的比特矩阵S4,1和S4,2。将x2作为LSM混沌系统的初始值，再对矩阵S4,1和S4,2做多重置乱运算。多重置乱算法如下。

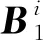
(15)

式中:i=1,2,…,MN/4。

(16)

综上所述，对于高血压合并动脉粥样硬化的患者，在治疗过程中辅以康复护理，可促进患者养成良好的生活习惯，并将血压水平稳定在正常范围内，预防疾病的进一步发展。

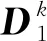
2.4 扩散加密

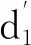
(17)

(18)

将矩阵P4与矩阵F1和F2做异或运算，得到大小为M×N的加密图像C。

C(g,h)=F1(g,h)⊕P4(g,h)⊕F2(g,h)

(19)

式中:g=1,2,…,M，h=1,2,…,N。

3 解密算法

(20)

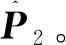
4 实验结果

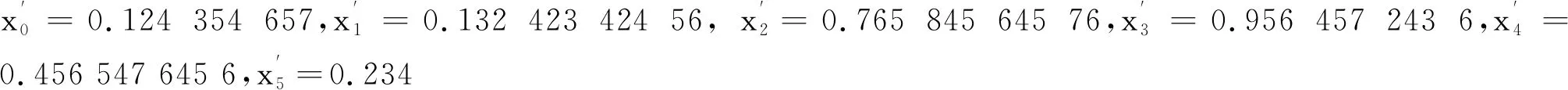
由文献[22]可将式(7)写成：

(21)

采用大小为256×256的Lena、Pepper和Cameraman测试图像，如图2(a)～(c)所示。利用本文加密算法，得到对应的加密图像，如图2(d)～(f)所示，其中，r=0.75。采用本文的解密算法，得到对应的解密图像，如图2(g)～(i)所示，解密图像的峰值信噪比(peak signal to noise ratio,PSNR)分别为：图2(g)为34.171 9 dB，图2(h)为29.568 4 dB，图2(i)为29.473 2 dB。实验结果表明，加密图像中无法看出任何原始图像的特征和规律性，解密图像和原始图像没有显著的差异。

(a) Lena原始图像 (b) Peppers原始图像 (c) Cameraman原始图像

采用不同的压缩比，分别利用本文构造的测量矩阵和文献[11]中生成的随机测量矩阵，采用本文的加密算法，分别对Lena图像加密，得到对应的加密图像和解密图像，计算解密图像的峰值信噪比和平均结构相似性(structural similarity,SSIM)，结果如表1。可以看出，采用不同的压缩比例，利用本文构造的测量矩阵的解密算法得到解密图像的峰值信噪比和结构相似性优于文献[11]。实验结果表明本文构造的测量矩阵具有更好的重构性能。

5 算法性能分析

5.1 密钥空间

5.2 直方图

明文图像的直方图会表现出较明显的特征分布，加密图像的直方图则是平滑均匀分布[20]。Lena、Peppers和Cameraman原始图像的直方图如图3(a)、(c)、(e)所示。采用本文加密算法，得到相应加密图像的直方图如图3(b)、(d)、(f)所示。实验结果表明，原始图像的灰度级分布具有明显的特征，加密图像中的灰度级分布比较均匀，表明本文的加密算法能够有效地抵御统计攻击。

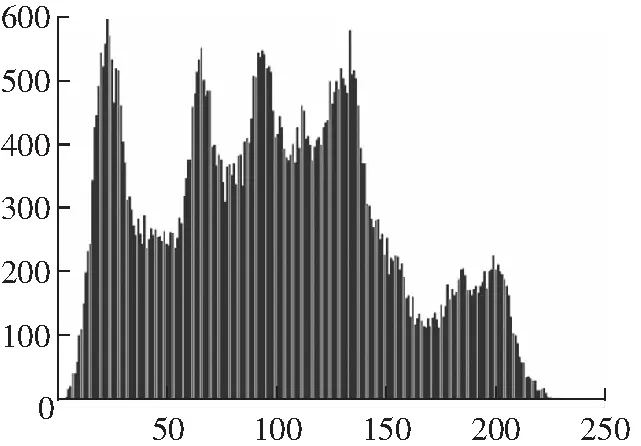
(a) Lena原始图像

5.3 相关性分析

图像的相关性表示图像中相邻像素之间的关联程度[20]。为了衡量相邻像素之间的相关性，计算图像中相邻像素的相关系数，即：

(22)

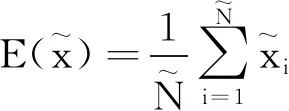
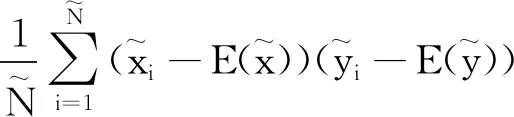
Lena原始图像在水平、垂直和对角线3个不同方向上相邻像素的相关性分布如图4(a)、(c)、(e)所示。采用本文加密算法，得到Lena加密图像在水平、垂直和对角线3个不同方向上相邻像素的相关性分布如图4(b)、(d)、(f)所示，实验结果表明采用本文的加密算法降低了图像像素之间的相关性。

(a) Lena原始图像的水平方向

为了验证本文算法的性能，本文采用文献[15]和文献[21]作为对比基准算法。文献[15]将Logistic映射、Tent映射和Sine映射组合成一种新的一维混沌映射，并利用该混沌映射生成的随机序列作为种子序列生成非相干旋转混沌测量矩阵，利用该测量矩阵对图像的离散小波变换压缩采样，得到测量值矩阵。最后，将测量值矩阵利用一维混沌映射生成的随机序列重新排序实现图像的加密。文献[21]对明文图像做离散小波变换，得到该图像的稀疏表示。然后采用Chebyshev映射构成服从高斯分布的测量矩阵，对明文图像的稀疏表示压缩采样，得到测量值矩阵。最后，将测量值矩阵与四维混沌映射生成的随机矩阵做异或运算实现图像的加密。

分别计算Lena、Peppers和Cameraman原始图像、经过本文加密算法以及文献[15]和文献[21]的加密算法得到相应的加密图像在水平、垂直和对角线3个不同方向上相邻像素的相关性系数，结果如表(2) 所示。可以看出，原始图像中相邻像素的相关系数接近于1，而利用本文加密算法得到相应的加密图像中相邻像素的相关系数接近于0。并与文献[15]和文献[21]对比，利用本文的加密算法得到的加密图像的相关系数在一定程度上更接近于0，实验结果表明本文的加密算法可以更好地降低图像相邻像素的相关性。

5.4 信息熵分析

信息熵是用于计算信息中不确定度，在灰度级为255的数字图像中，完全理想的随机图像中信息熵为8。计算图像信息熵的方式如下：

(23)

表2 原始图像和加密图像中相邻像素的相关系数

5.5 密钥敏感性分析

密钥敏感性分析用于检测当解密密钥发生微小变化时，对比正确与变化后的解密密钥所得到的不同解密图像之间的差异程度。本文使用House加密图像作为测试图像，将前4组解密密钥分别减去或加上10-14微小变化后得到5组改变后的解密密钥。并利用这5组改变的密钥依次采用本文得解密算法得到相应的House解密图像，结果如图(5)所示。实验结果表明，只有使用正确地解密密钥才可以解密出原始图像，即使密钥有微小的变化，也不能从加密图像中正确的解密出原始图像，表明本文提出的加密算法对密钥有很高的敏感性。

表3 原始图像和加密图像的信息熵

5.6 抗噪声攻击

本文在Lena加密图像中添加不同强度的椒盐噪声，利用本文的解密算法，得到相应的解密图像，其结果如图(6) 所示。并计算相应的解密图像的峰值信噪比，分别为图6(a)PSNR为33.682 9 dB；图6(b)PSNR为15.576 0 dB；图6(c)PSNR为9.930 3 dB。实验结果表明，随着噪声强度的增加，椒盐噪声对解密图像的质量影响也在增强，但在一定条件下，从解密图像中可以看出原始图像的信息，说明本文提出的加密算法对椒盐噪声具有一定的抗噪能力。

(a) 正确密钥

(a) 强度0.000 01 (b) 强度0.000 1 (c) 强度0.000 5

6 结论

本文提出了一种基于压缩感知和位平面多重置乱的图像加密算法。该算法利用混沌系统和非线性函数生成测量矩阵，利用生成的测量矩阵对图像的DCT变换压缩采样，得到压缩加密图像。采用不同的切割重组方式将压缩加密图像重组，得到比特矩阵。再对比特矩阵多重置乱，得到置乱图像。再对置乱图像做扩散运算，实现图像的加密。实验结果表明本文的加密算法具有较大密钥空间、较低的相邻像素相关系数、较高的密钥敏感性、较高的信息熵和抗噪声攻击等性能。