卖空限制和分红约束下DC养老金计划的最优投资

余 鑫，王传玉，何学强

(安徽工程大学 数理与金融学院，安徽 芜湖 241000)

养老金计划主要分为两类：固定收益(DB)计划和固定缴款(DC)计划。在DB计划中，退休金是预先确定的，退休金计划参与的供款也要确定，然后进行调整以使资金保持平衡。与DB计划相关的财务风险由计划发起人而不是计划成员承担。在DC计划中，仅定义了供款(通常是工资的固定百分比)，而雇员的退休福利则由退休时积累的金额决定。与DC计划相关的财务风险已从发起人转移到了缴款者。近年来，DC计划在养老金市场中变得越来越受欢迎。DC养老金计划的退休福利主要受退休前投资组合的表现所影响。定缴款计划的退休福利主要受退休前基金组合的表现所影响。资产配置决策是养老金积累阶段风险管理的重要内容。具有不同目标的DC养老金计划的最优投资策略，以及预期效用最大化的运用，已在文献中进行了广泛讨论。由于DC养老金计划的投资时间通常很长，因此一些研究将通货膨胀风险纳入了模型。例如，Zhang等研究了具有DC养老金基金通胀风险的最优资产配置。Han等分别讨论了在CRRA效用最大化和均值-方差准则下具有通胀风险的最优DC计划管理的连续时间优化模型。

由于养老金计划的目的是为成员提供足够的退休收入，因此一些研究将投资组合保险(PI)约束纳入DC养老金的投资问题中，参见Boulier和Cairns。PI约束可以通过对保险合同施加最低保证来增强对保单持有人或养老金成员的保护。具体而言，绩效指标约束要求经理在退休时将投资组合价值保持在最低担保之上，这对成员的福利至关重要。最低保证的一种流行形式是其退休成员的最低年收入，参见Boulier、Guan等将平均预期寿命延长到具有确定性死亡率的随机时间。

王传玉等研究了通胀环境下带有红利和最低收益保障的确定缴费(DC)型养老金计划的最优投资问题。应用伊藤公式得到通胀折现后的真实财富过程，在DC型养老金计划终端财富内部保障约束下，即终端财富始终超过最低收益保障，考虑通胀环境下的退休时刻终端财富期望CRRA效用最大化问题。应用HJB方程推导得到了退休前任意时刻DC型养老金计划最优投资策略的显式解，分析了不同参数对最优投资策略的影响，为DC型养老金计划投资者提供更有效的策略。孔焕等研究了带有不确定收益的保险公司在离散时间点的最优分红问题。引入不确定收益项和风险系数，并在指数保费原则下构建了贴现收益，研究了有限时间和无限时间范围的最优分红策略，证明最优分红策略是一个波段策略。最后,给出一些数值研究，并讨论了不同风险系数对最优分红策略的影响。

S型效用函数是指效用函数在一定财富或收益水平下是凸函数,而在一定财富或收益之上则是凹函数，通过S型效用函数还可以说明财富减少给人们带来的效用降低程度比因财富增加带来的效用增量更大。李波研究了在Kahneman等提出的预期理论的框架下的最优投资策略选择问题，在连续时间情形下依据预期理论的原则，用S型效用函数去表示投资者对待收益和损失时不同的态度。Servvas推导了具有期望理论偏好的个体的最优动态消费和投资组合选择,证明了最优消费策略对经济冲击是相当不敏感的,证实了具有预期理论偏好的个人通常会实施(非常)保守的投资组合策略,并讨论了研究结果对投资相关年金产品设计的影响。

基于Dong提出的在卖空限制和投资组合保险下DC养老金计划的最优投资问题，进行了进一步的改进，设置了新的资产组合模型，运用对偶控制方法来解决问题，帮助管理者管理风险。研究是在卖空限制、分红约束两个条件下，利用S型效用函数对金融市场进行研究。所研究的资产组合，即无风险资产以及成员进行分红后的风险资产，并且描述了卖空限制和分红约束如何影响最优终端财富和最优策略。

1 模型假设与构建

从Dong的研究中，假设金融市场是一个非自融资的完备市场，在卖空限制和分红约束下，定义一个完备概率空间(

Ω

,

F

,{

Ft

}

t

∈[0,

T

],

P

)，其中{

Ft

|

t

∈

T

}包含市场中

t

时刻之前可得的信息。考虑连续有限时间

t

∈[0，

T

]的时间模型。假设所有的变量和随机过程在这个概率空间中。养老金从时间0开始，退休时间为

T

。

W

(

t

)为标准布朗运动，价格水平过程为

P

(

t

)，并假设

P

(

t

)服从随机微分方程：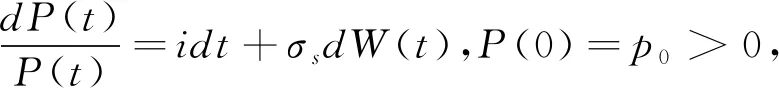

(1)

式中，

i

>0是预期的通货膨胀率，而

σ

>0是价格水平的波动性。假设金融市场由两种交易资产组成：无风险资产、成员进行分红后的风险资产。无风险资产

M

(

t

)服从随机微分方程：

(2)

式中，

r

是固定的无风险名义收益率。风险资产

N

(

t

)服从随机微分方程：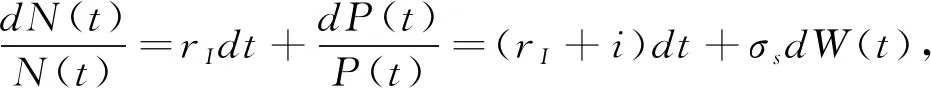

(3)

(4)

式中，ϑ和ϑ分别是无风险资产和风险资产的市场价格。

在DC计划中，养老金成员在退休时间

T

之前向养老金计划连续缴款，并且假定在时间

t

缴纳给养老基金的金额为

c

(

t

)>0，其中

c

(

t

)是时间

t

的指数函数。养老金帐户的初始财富

X

>0，令

π

(

t

)和

π

(

t

)分别是投资于风险资产和无风险资产的数量。考虑对风险资产进行分红，假设缴款单位是1，单位时间内每单位货币在风险资产上所得的分红记为

δ

，

t

时刻养老金账户资产为

X

(

t

)，投资到风险资产的比例为

π

(

t

)，投资到无风险资产的比例为

π

(

t

)，则养老金的财富过程满足以下微分方程：

(5)

假设养老金的最低收益保障为

L

，我们的目的是在风险资产和无风险资产中找到最佳分配，以使终端财富效用最大化，即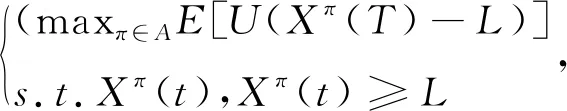

(6)

式中，

U

是[0,∞)上的连续递增函数，对于

U

(

x

)=-∞，

x

<0，

L

是一个正常数，表示成员退休时的一次总付。为了描述人们相对于一个最低收益保障参考点的不同的得失行为，即避险胜于收益，风险寻求胜于损失。研究采取

S

型效用函数，它在[0,∞)被定义为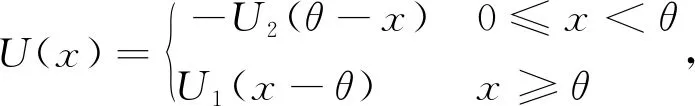

(7)

式中，

θ

是一个参数，且

θ

>0，

U

和

U

严格递增，连续可微并且在[0,∞)上满足

U

(

x

)<

U

(

x

)且

U

(0)=0。当

x

<

θ

时，

U

是凸的，当

x

>

θ

时，

U

是凹的，这表明人们在收益方面倾向于避险，对损失则倾向于寻求风险。

2 模型求解

利用对偶控制方法研究效用最大化问题。效用函数(7)和参数的限制由Kahneman的实验和统计数据支持，通常用于效用最大化问题。参照Guan等，当不允许卖空时，不能使用鞅方法。

设效用函数

U

(

x

)的对偶函数为

V

(

y

)=sup≥0{

U

(

x

)-

xy

},

y

>0，

(8)

设凹包络

U

为

V

(

y

)=sup≥0{

U

(

x

)-

xy

},

y

>0，

(9)

取

I

(

y

)为

U

的反函数，

I

(

u

(

x

))=

I

(

V

(

y

)+

y

)，得到

(10)

由Reichlin的引理2

.

9可得，对于

y

>0，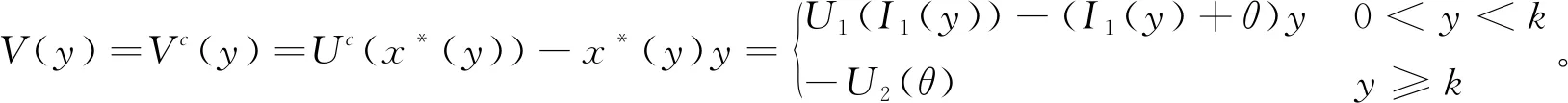

(11)

由于

c

(

T

)>0的财富过程不是自筹的，对于

c

(

T

)=0的财富过程，Boulier等的对偶控制方法无法直接应用，因此将优化问题转换为具有控制约束的经典投资组合优化问题。从

t

到

T

的总养老金缴款的时间

t

的贴现值为

(12)

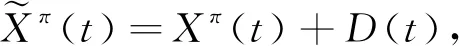
(13)

由财富过程式(5)得到

(14)

由Bian的引理3

.

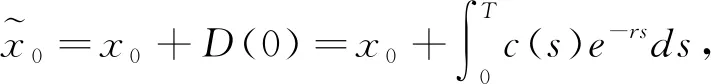
1，采用非负上鞅过程

Y

构造

Z

(

t

):=

X

(

t

)

Y

(

t

)，0≤

t

≤

T

，

(15)

给出对偶过程

dY

(

t

)=

Y

(

t

)(-

rdt

-(

σ

υ

(

t

)+

ξ

)

dW

(

t

))，

Y

(0)=

y

，

(16)

由于

Z

(

t

)是一个上鞅过程，且

V

是

U

的对偶函数，有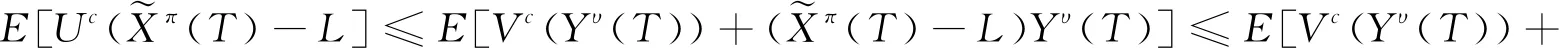

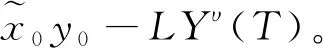
(17)

考虑对偶最小化问题

inf∈

E

[

V

(

Y

(

T

))-

LY

(

T

)]，

(18)

对于0≤

t

≤

T

且

y

>0,构造对偶值函数

υ

(

t

，

y

)=inf∈

E

[

V

(

Y

(

T

))-

LY

(

T

)，

Y

(

t

)=

y

]，

(19)

对偶HJB方程为

(20)

式中，

V

(

y

)=

V

(

y

)，

y

>0。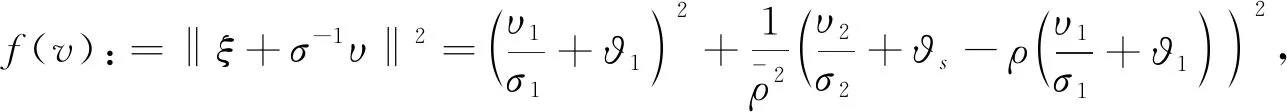

(21)

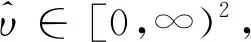
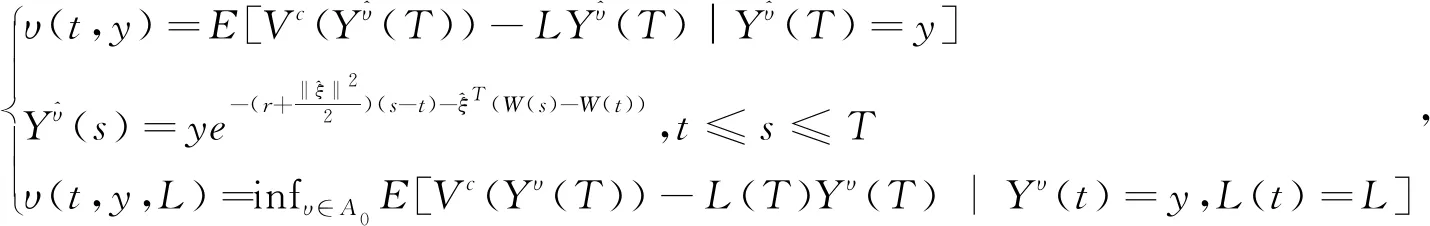
(22)

利用Bian定理3

.

8的最优对偶控制原理，得到最优策略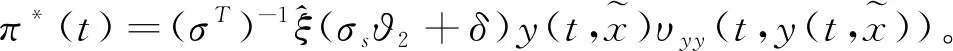

(23)

令

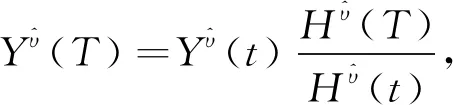
(24)

对于∀

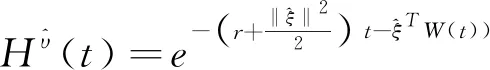
λ

∈

R

,

h

>0,

y

>0，有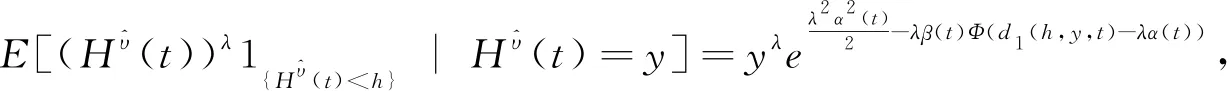

(25)

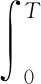
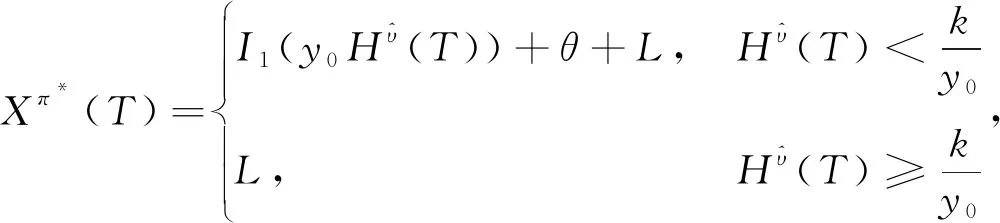
(26)

最优的财富过程为

(27)

其中,

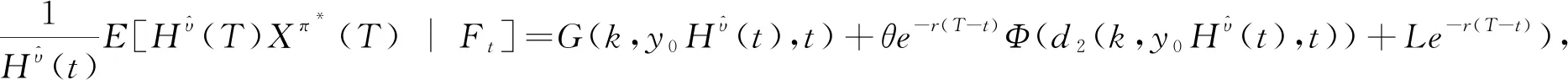
(28)

φ

是标准正态密度函数，0<

t

<

T

。

d

(

k

,

y

,

t

)=

d

(

k

,

y

,

t

)-

α

(

t

),

α

(

t

)、

β

(

t

)、

d

(

k

,

y

,

t

)均由式(27)定义。在假设式(27)和式(30)中，令

z

=0，

k

=∞，且

d

(

k

，

y

，

t

)=∞。最优终端财富为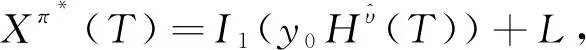

(29)

对于

θ

>0，有

P

(

X

(

T

)=

L

)=1-

Φ

(

d

(

k

，

y

，0))，

(30)

式中，

k

是由

k

=

U

(

z

-

θ

)所确定的。

定理

1

若

θ

=0，效用函数

U

(

x

)=

U

(

x

)，

x

≥0(取

U

是因为

x

≥

θ

的情况下

U

(

x

)才能取正，如式(7)所示)，则最优终端财富的简化表达式为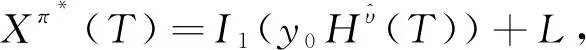

(31)

若

θ

>0，则最优终端财富达到最低收益保障

L

的概率为

P

(

X

(

T

)=

L

)=1-

Φ

(

d

(

k

，

y

，0))，

(32)

式中，

k

是由

k

=

U

(

z

-

θ

)所确定的。此处给出定理，令

P

(

X

(

T

))=

L

，在下一部分对结果进行数值分析。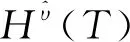

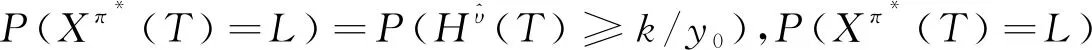
3 数值分析

在这一部分中，将进行一些数值计算，以研究在卖空限制和分红约束下，不同的参考点

θ

对最优终端财富的影响以及分红参数

δ

对最优策略的影响。为了说明参考点

θ

如何影响最优终端财富，令

T

=40，

r

=0

.

01,

r

=0

.

02,

i

=0

.

03,

μ

=0

.

05,

σ

=0

.

1,

σ

=0

.

2,

ρ

=0

.

75,

L

=0(模型中的参数值取自YingHui Dong)。最优终端财富

P

(

X

(

T

)=0)和

θ

之间的关系如图1所示。由图1可见，当参考点

θ

增大时，

X

(

T

)=0的概率增加。这是因为

P

(

X

(

T

)=0)衡量了经济状况较差的情况，并且

θ

值较大的时候会扩大损失的范围。当

θ

较小时，

X

(

T

)=0的概率较小，我们也可以看到

P

(

X

(

T

)=0)在卖空限制下大于允许卖空限制的情况，原因是投资者在卖空约束下对投资策略的选择较少。

E

(

X

(

T

))与

θ

之间的关系如图2所示。由图2可见，允许卖空限制期望大于禁止卖空限制期望。这是因为如果投资者把他最初的盈余和缴款都投入到无风险资产中，那么期望就会达到一个最低水平。当参考点相当低(低于最低收益保障)时，参考点的减少导致投资于每个风险资产的财富比例增加，因为投资于无风险资产时非常容易达到低参考点。当参考点大于这个最低收益保障时，投资者为了寻求更多的风险，将更多的钱投入到风险资产中，以帮助管理者有效地管理并降低风险。最优投资策略

π

(

t

)与

δ

之间的关系如图3所示。由图3可见，随着分红的出现及增长，最优投资策略也逐渐增加。出现这样的结果是由于在财富过程的风险资产上添加了分红约束，投资者为了寻求更高的收益而改变投资策略，将更多的资产投资于风险资产当中，导致最优投资策略发生了改变。

图1 最优终端财富P(Xπ*(T)=0)和θ之间的关系图2 E(Xπ*(T))与θ之间的关系

图3 最优投资策略π*(t)与δ之间的关系

4 贡献与展望

研究卖空限制和分红约束下DC养老金计划的最优投资问题，通过对偶控制方法，建立财富过程，应用HJB方程求解，最后通过给定参数，并进行数值模拟。在此前的研究中，并没有考虑到分红约束的因素对投资策略所产生的影响，而分红约束在现实中实际存在。所以研究也更符合实际情况并且适用于金融市场存在分红的情况中。研究结果表明卖空限制以及分红约束有效地改善了DC养老金计划的最优投资问题。

研究的主要贡献是在考虑卖空限制的情况下，增加了分红约束的因素来对金融市场中的DC养老金计划进行建模。我们所采用的S型效用可以更好地反映养老金计划的管理者对风险的态度，因为它包括了风险规避以及寻求损失的风险。为了更好地保障成员的利益免受管理者的影响，将投资组合保险加入到模型中，通过建立对偶控制过程，并应用HJB方程进行求解，得出了最优财富过程和最优投资策略的显式表达式。理论和数值结果表明，卖空限制以及分红约束的加入，使得最优终端财富和最优策略发生了变化，这样会导致收益的增加，同时也会增加管理者在投资过程中所承担的风险。此外，研究模型也可以进行一些其他的拓展，在未来的研究中，我们也可以考虑连续缴费和最低保障遵循某些随机过程。