基于二次滑模观测器的直线电机无传感器控制

陈俊宏

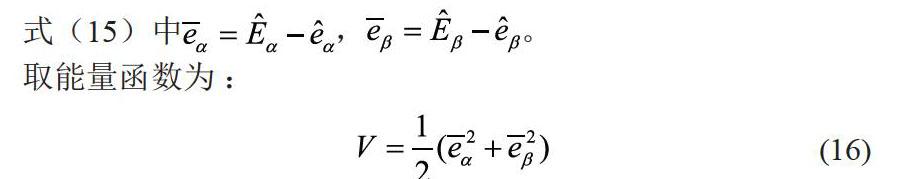
[中图分类号] TP273

[文献标志码]A

[文章编号]2095-6487 （2021） 02-0118-03

Sensorless Control of Linear Motor Based on Secondry Sliding Mode Observer

Chen Jun-hong

[ Abstract] As the”eye”of the PMLG system， whether the sensor can operate normally is of decisive significance to the system.. Mechanicalsensors， such as speed sensors， are greatly affected by the harsh environment， especially in the case of humid ocean，they are prone to failure. This papermainly srudies the speed sensorless control strategy based on secondry sliding mode observer， and carries out experimental simulation research throughMATLAB， Simulink simulation platform.

[ Keywords] Sensorless control;Sliding mode observer;PMLG

在永磁直线发电机的控制中，动子的速度及位置检测，通常是依赖于光电编码器等机械式传感器，不仅增加系统成本，而且在恶劣环境中长期运行，无法保证传感器的准确性及可靠性。为解决该问题，较多学者在无传感器的控制开展研究，基本原理是通过检测电机运行时的电压电流信号，从而估算转子（动子）的位置和转速[1]。估算的策略主要分为两种：一类是基于基波励磁和反电动势的估测万法，主要适用于电动机的中高速矢量控制[2-3];另一类是基于电动机凸极效应和信号注入的各种方法，土要用于低速和零速下的转子位置及转速估计[4]。

针对永磁直线电机，提出一种基于二次滑模观测器的无速度传感器控制策略，详细介绍了原理，并基于Matlab/Simulink仿真下台对该策略进行仿真。仿真证明该策略具有较好的性能，控制效果好。

1 滑模观测器原理

1.1 滑模控制基本理论

滑模观测器的基础来自于滑模变结构控制，通常情况下，系统的n阶状态空间中，存在这样的曲而s（x）一（x1，x2，x3，……，X），这曲线把状态空间分割成上下两部分：s>0和s<0，系统运动点从外部运动到曲面上，并最后趋近于某点，属于滑模状态。当曲面上某一区域内所有的点都是属于该类运动，就称为“滑模区”，系统在滑模区中的运动就称为“滑模运动”。滑模控制的最终目标就是找到能够使系统状态按照预设轨迹运动的控制函数。

1.2 滑模观测器原理

滑模观测器是参考滑模变结构的思想，将龙伯格状态观测器回路替换成滑模变结构的控制形式得到的。

存在系统，其状态方程如下：

式（1）中，A、B、D都是已知的参数矩阵，x为状态变量;y为输出变量;u为系统控制输入。觀测器输出与实际系统输出进行比较得出偏差，通过反馈回路与观测器给定值作差送入滑模控制器，得出重构等效控制。通过滑模器，对观测输出与实际自的差值进行强迫运动，跟踪零给定，最后使观测状态与实际状态保持一致，达到以重构状态代替观测状态的效果。

2 无传感器控制策略改进及仿真

2.1 改进滑模观测器的设计

式（2）是在两相静止坐标下的永磁直线电机数学模型。

可以通过式（3）直接推导出动子速度与加度的人小，其基本原理如式（4）所示：

选取Sigmoid函数日（x）作为切换函数。设计滑模观测器，可得定子电流估计值与实际的误差方程为：

式（5）中：ia.ib为定子电流估计值;K为控制率的增益;日（x）为开关函数。构造滑模而Sa=ia-ia、SB=iB-iB

根据李雅普诺夫稳定性条件验证式（5）构成的滑模观测器，可知满足李雅普诺夫稳定性条件，需要取滑模增益K>max 1ea1，1eBl}，此时反电动势的估计值为：

式（6）表示通过输入Ua、UB、ia、iB到滑模观测器里得出的反电动势估算值，是关于电流估计值与实际电流值误差的开关函数，通常记为：

对式（7）进行初步的低通滤波下滑，减少由于控制率切换等因素带来的反电动势估计值信号尖峰，避免对系统产生过人冲击，可得经过滤波后的反中.动势的估计值为：

式（8）中，m，是低通滤波器的截止频率。

由式（5）、式（8）可以推导得出，通过反电动势估计值推出的动子位置角为：

低通滤波器带有相位延迟环节，其延迟与截止频率和输入信号频率有关，可以根据该关系得出应该补偿的相位为：经过补偿后的位置加为：动子的速度为：

2.2 结合二次观测的滑模观测器设计

上文得出的反电动势估计值，经过低通滤波器后会相位偏移，常用办法是相位补偿，但无法精确补偿。利用反电动势的动态模型，设计观测器对低通滤波器的输出进行二次估计，能够得到较精准的动子位置角和动子速度。

对式（3）进行求导，忽略动子速度v在较小时间段内的微小变化，即dv/dt=O，可得：

构造反电动势的二次观测器，同时引入二次观测值到一次观测输入端，可得：

式中，L是正常数，Ea和EB是反电动势的二次观测值Ua和UB是一次观测器的实际输入。

结合式（13）与式（14），Wr=Wr-Wr，得：对能量函数V求导，结合式（15）可以看出：

3 仿真实验

仿真研究侧重在滑模观测器中动子位置如速度估计值的精确度，因此通过建立速度闭环来验证本章提出方法的有效性。

仿真永磁直线电机参数如下：电感系数Ld=Lq=8.3 mH，定子三相对称电阻Rs=6.48 Q，极距T的值为0.05m，极对数～为8，永磁体磁链f的值是0.147Wb;给定速度为1m/s，仿真时间为Is，K值取100，，值取5。

速度观测器为经典滑模观测器、结合二次观测环节的改进滑模观测器，仿真结果与分析如下。

经典滑模观测器采用sign （x）作为切换函数，仿真效果如图1所示。图1 （a）和图1（b）中，动子速度估计值在实际值上下范围内的抖振非常人，不符合系统对速度值的要求。图1 （c）、图1 （d）分别为转子位置角实际值仿真图、估计值仿真图。可以看出位置如的估计不仅有很大的抖振，与实际值的误差也很人。如图2所示，为结合二次观测和改进切换函数的滑模观测器（上接第119页）仿真结果。图2 （a）中为动子实际速度，图2（b）中为动子速度值。可以看出，虽然增加了二次观测环节，但是对改进滑模观测器的速度估计没有影响。图2 （c）、图2（d）是转子位置如實际值、估计值。从中可以看出，二次观测后的滑模观测器得出的转子位置角，不仅幅值及变化速率与实际值保持一致，而且相位上的延迟问题得到有效改善。

4 结束语

本文介绍了滑模观测器的原理及其应用。引入sigmoid函数代替开关函数Sign （x），作为切换函数，有效地抑制滑模运动中因切换函数不连续引起的抖振。为解决低通滤波器所带来的相位延迟，反电动势的动态模型，引入观测器作为二次观测环节，对其输出进行二次观测。试验结果表明该策略对相位延迟问题有良好的修正作用。

参考文献

[1]陈广辉，曾敏，魏良红，无位置传感器永磁同步电动机矢量控制系统综述[J]微特电机，2011，39 （12）：64-67

[2]付勋波，张雷，胡书举，等模型参考自适应无速度传感器技术在永磁直驱风力发电系统中应用[J]电力自动化设备，2009，29（9）：90-93