离心-振动复合校准技术研究
董雪明,王敏林
(航空工业北京长城计量测试技术研究所,北京 100095)
0 引言
随着航空、航天工业的飞速进步,对飞行器等运载工具的性能要求越来越高,由于飞行环境复杂和技术现状限制,现实需求与研究水平存在着很大的差距,例如火箭、导弹的发射会处在一种振动[1-2];线加速度、阵风、过载等同时作用的复杂动态环境[3]中,这会影响飞行器导航系统的性能,造成精度下降、性能失效,甚至会损坏。而过去受设备条件限制所进行的可靠性、功能性、精度性测试试验,严格地说是对某一项环境因素的单独模拟检验,如振动试验或过载试验等,很难综合反映运载工具飞行时的工作状况,因此有必要研究建立一套离心-振动复合加速度试验系统,尽可能模拟真实的飞行环境,为研究相关的“天地一致性”[4]问题提供保障。
在离心-振动复合加速度试验装置的研制方面,国外早已开始进行相关研究,并有用于环境试验的产品问世。例如,美国Sandia国家实验室研制的“8.84 m离心-振动设备”[5-6]、美国Wyle实验室研制的“安装单轴电磁振动台系统的离心机”[7]、法国Actidyn公司生产的离心-振动产品,能够实现正弦振动、随机振动、冲击、多正弦和暂态多种振动控制模式[8]。我国多参数复合校准技术研究刚刚开始起步,中国工程物理研究院已经研制出离心-振动复合环境试验装置[9],浙江大学从国外引进了离心-振动复合环境试验装置[10]。综上所述,国内外目前的研究成果大多数用于可靠性试验的离心-振动复合试验机,没有用于开展加速度计复合校准的装置。
为解决飞行器、火箭弹、水中兵器、无人机等领域惯性器件的“天地一致性”校准有关难题,我所在2015年成功研制了离心-振动复合校准装置。本文对此离心-振动复合校准装置进行详细介绍,建立离心-振动复合校准模型,并分析离心-振动复合下的动不平衡影响。
1 标定目的
目前,我国没有任何用于复合环境下开展惯性器件计量校准的装置,这严重制约了军工装备惯性器件的研制和生产水平及能力的提升,影响和限制了武器装备的打击精度和使用寿命。因此,本文建立基于离心-振动复合校准装置的校准方法,模拟真实的加速度计校准环境,以提高复合环境下加速度计的校准精度。
2 标定原理
2.1 离心-振动复合校准装置系统中的动不平衡问题研究
离心-振动复合校准装置是以精密离心机为基础平台,搭载电磁振动台构成的多部件复合型惯性测试设备。此类设备存在的一个典型问题就是各个组成部件之间的相互影响[13],在离心-振动复合校准装置系统中,由于被测单元及其工装随着振动台的活动部件进行周期性运动,会引起离心机的动不平衡问题。
动不平衡问题是旋转机械研究中的关键问题,主要是因为转子质量分布不均引起的。严重的动不平衡问题会导致转轴和轴承之间产生振动,直接影响旋转机械的工作效率和可靠性。
解决动不平衡问题的基本思路是对失衡转子进行配重,使配重产生的离心力抵消转子原有不平衡量产生的离心力;或者精确测出不平衡量的位置和大小,在相应位置去掉不平衡质量。一般情况下,以上两种方法都能解决动不平衡问题。但是,在离心-振动复合校准装置系统中,以上两种方法都不可行,因为上述两种方法针对的动不平衡量都是“静止”的,即动不平衡量的位置和数值不随着时间变化,而离心-振动复合校准装置系统中的动不平衡量是“运动”的,即随着振动台的运动,该动不平衡量将产生周期性的位置变化和数值变化。除非采用同步的动态配重方法,否则不可能得到解决。这是一个特殊的新问题,就目前的研究而言,还没有切实的解决措施。但是,我们可以通过分析,评估这种动不平衡的影响,通过机械结构的设计来削弱这种影响。
理论上,离心-振动复合校准装置的动不平衡问题在垂臂振动情况下不存在,而在顺臂振动情况下最为显著。下面针对离心-振动复合校准装置顺臂振动情况下的动不平衡问题进行分析,评估其对离心-振动复合校准装置输出加速度的影响。首先对顺臂振动时的受力情况进行分析,如图1所示。振动台动圈、夹具和被测单元(总称为“活动部件”)总质量为m,简化为质心M。质心静止时距离离心机转轴中心线距离为R。
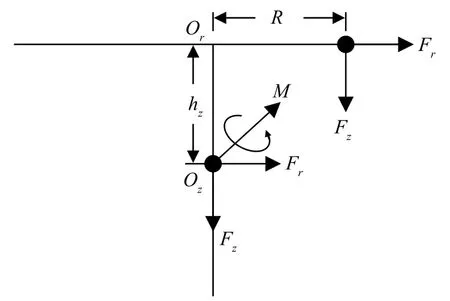
图1 顺臂振动受力示意图
设质心做线振动运动,且初相位为0,满足方程
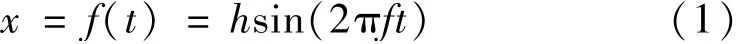
式中:x为系统状态;t为时间;h为振动台振幅;f为振动频率。则质心距离离心机旋转轴的距离为

质心位置变化会造成离心机不平衡,相当于离心机两端质量未配平的情况。为便于理解,这里定义一个位置固定在L,质量为me的“等效偏载质量”,满足

根据公式(2)和(3),得到等效偏载质量为

若设离心机转速为Ωrad/s,则me受到惯性力(方向为沿离心机旋转半径方向向外)大小为

且受到的重力大小为

为便于分析,将me产生的惯性力和重力平移到距离心机旋转主轴轴心Oz处。根据力的平移定理,作用在刚体上的力可平移到刚体任一点,但必须同时附加一个力偶,其力偶矩是原力矩对于新作用点之力矩。设离心机旋转主轴长度为2h,平移之后,me在Oz处除了受到大小相等、方向相同的惯性力与重力作用以外,还受到力矩的作用。将两个力对应的力矩合成,得到合力矩M

由动不平衡产生的惯性力和惯性力矩,将使离心机的工作半径变化。离心机受动不平衡问题的影响如图2所示。

图2 离心机动不平衡示意图
因惯性力的作用,离心机旋转轴线产生的径向偏移量

式中:Kr为气浮轴承的径向刚度,N/m。力矩M使得主轴产生的主轴倾斜角为

式中:Kθ为气浮轴承的角刚度,Nm/rad。重力作用于竖直方向,不对主轴径向姿态产生影响。
若在质心处安装线加速度计,线加速度计输入轴与离心机臂平行。在不平衡状态下工作的离心机,其工作半径变化量为

式中:ΔRr为由惯性力Fr作用引起的径向偏移量;ΔRM为由力矩M作用引起的离心机主轴几何轴线在加速度质心所在平面上的位移量
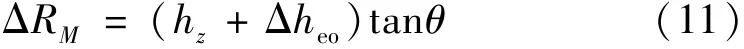
式中:Δheo为偏载质量质心所在平面与O点的垂直距离,在安装时确定。根据式(5)至式(10),可以得到动不平衡对加速度计工作半径的影响量为
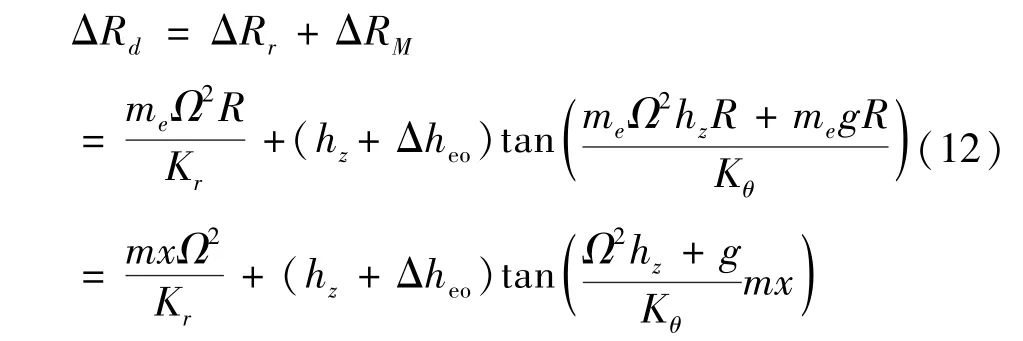
根据公式(5),(6),(7)和公式(9),动不平衡引起离心机主轴的俯仰失准角为
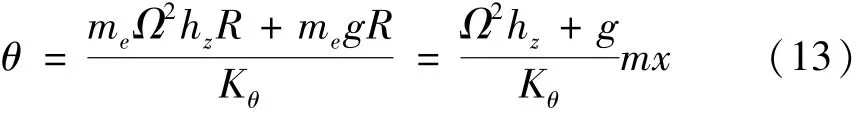
离心-振动复合校准装置的设计参数如表1所示。根据表1设计参数,计算得到俯仰失准角的最大值为

表1 离心-振动复合校准装置设计参数
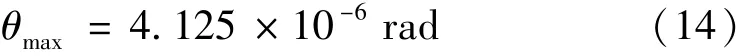
现有安装工艺能够保证圆盘与主轴轴线的不垂直误差小于10″,约4.848×10-5rad。因此,在现有的离心-振动复合校准装置配置下,动不平衡引起的离心机主轴失准角将被安装误差所掩盖。
同样根据表1设计参数,计算得到动不平衡对加速度计工作半径的最大影响量为
这一影响量的数量级与离心机动态半径变化数量级相当,需要做进一步分析。
理想情况下,离心机产生的加速度大小可以表示为

因为动不平衡的影响,离心机加速度的输出变为
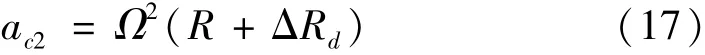
因此得到动不平衡引起的离心机加速度相对误差表达式为

根据公式(14)的估算,公式(13)表示的角度是小角度,因此,公式(12)中表示的ΔRd可以表示为
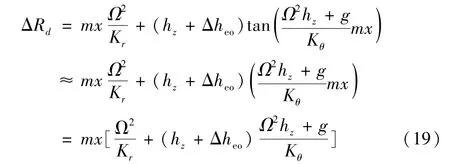
根据公式(1),(18)和公式(19)可知,动不平衡引起的离心机加速度相对误差表达式为

由公式(20)可知,当离心-振动复合校准装置机械参数固定时,动不平衡引起的离心机加速度相对误差是一个周期变量,其周期与振动台振动周期相同,其幅度与振动台的振幅h和离心机的转速Ω成正比。根据公式(15)的估计,离心机相对误差幅度为
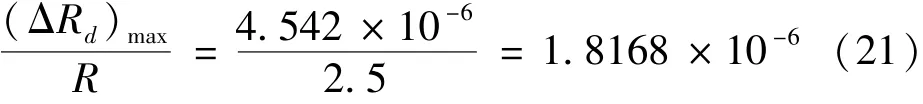
对于测量不确定度高于1×10-6量级的测试校准,这种影响限制了离心-振动复合校准装置的使用。在离心-振动复合校准装置机械结构固定的情况下,减小振动台振幅和离心机角速度,能够削弱这种影响。另外,根据加速度计整流误差模型的研究,由动不平衡引起的加速度误差是一个周期项,如果加速度计z轴方向与IA同方向,那么该误差项将导致额外的整流误差。即,经过整周期平均,加速度计的输出直流量平均值会比理想情况更大。
2.2 离心-振动复合模型
2.2.1 模型分析
本部分首先对离心-振动复合校准系统的输出加速度进行建模,以分析离心-振动复合校准系统的复合加速度复现能力。图3为离心-振动复合校准系统结构模型[14-15]。在离心机转臂(Centrifuge arm)上安装振动台(Vibrator),被测单元(Unit under test)安装在振动台台面上。振动台的振动方向与离心机转臂的旋转平面呈一定角度。这样的结构,通过离心机转轴(Rotation axis)的旋转输出恒加速度,通过振动台输出振动加速度。振动加速度与恒加速度以不同角度的组合,可以实现不同的多方向、恒加速度与振动复合的输入。
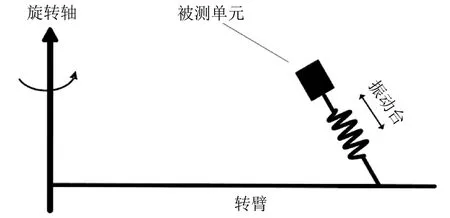
图3 离心-振动复合校准系统结构模型
为了明确离心-振动复合校准系统的输出,利用坐标的齐次变换推导其输出模型。坐标的齐次变换以变换矩阵的形式描述刚体间的相对空间关系,每个变换矩阵由旋转矩阵和平移向量组成,分别用于确定刚体的姿态和位移的相对变化。将刚体位移求对时间的二次导数,可以得到加速度。变换矩阵可以表示为

式中:A为旋转矩阵,描述坐标系之间顺时针的旋转变化引起的姿态改变,大小为3×3;D为平移向量,大小为3×1。在离心-振动复合校准系统中,除了振动台的弹性部件,都可认为是刚体。将加速度计安装在振动台台面上,建立坐标系如图4所示。通过以下步骤,完成从初始坐标系o-x0y0z0到加速度计坐标系o2-x2y2z2的变换:
1)建立离心机初始坐标系o-x0y0z0。初始坐标系是固定坐标系,表示离心机的理想初始状态。oz0竖直向上,ox0是离心机静止时摆臂的位置,通过右手定则确定oy0。
2)建立离心机坐标系o-x1y1z1。离心机坐标系是运动坐标系,表示离心机工作时的状态。设离心机的角速度大小为Ω,单位是rad/s,则从时刻0到t,离心机摆臂转过的角度为Ωt,则得到o-x1y1z1。
3)建立振动台台体坐标系o20-x20y20z20。振动台台体坐标系是固定坐标系,表示振动台的初始状态。由于离心机施加在加速度计上的加速度与振动台台体和离心机转轴的距离R无关,这里只考虑o-x1y1z1沿oy1方向的平移,使得oo20=R,就得到振动台台体坐标系。
4)建立过渡坐标系o20-x21y21z21和o20-x22y22z22。过渡坐标系是固定坐标系。通过振动台台体的两次坐标旋转来确定振动方向与离心机旋转平面的相对姿态。首先,振动台台体坐标系绕o20y20,旋转一定角度βrad,得到过渡坐标系o20-x21y21z21,然后过渡坐标系o20-x21y21z21绕着o20x21旋转角度αrad,得到过渡坐标系o20-x22y22z22。
5)建立加速度计坐标系o2-x2y2z2。加速度计坐标系是固定坐标系。设振动台的振动幅度是H(t),通过过渡坐标系o20-x22y22z22沿o20z22平移,使得o2o20=H(t),则得到加速度计坐标系o2-x2y2z2。
以上步骤对应的旋转矩阵和平移向量见表2。其中O3×1表示大小为3×1的O向量,I3×3表示大小为3×3的单位矩阵。上标“T”表示矩阵转置。
根据上述坐标变换步骤,可以得到成从初始坐标系o-x0y0z0到加速度计坐标系o2-x2y2z2的变换矩阵为
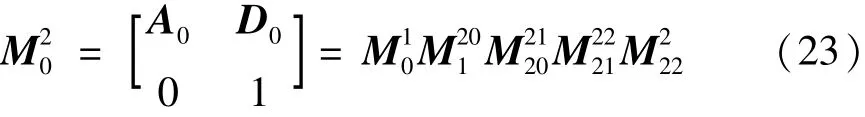
将表中的相应表达式代入公式(2),可以得到
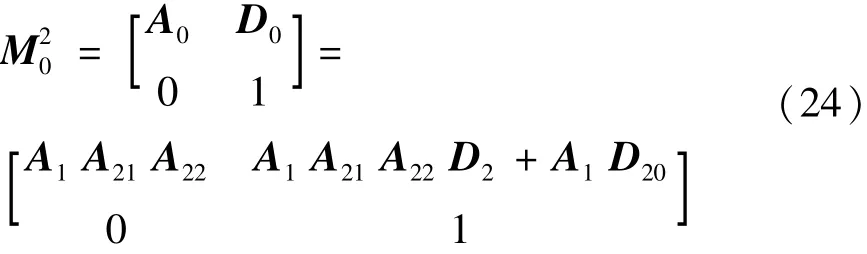
所以,
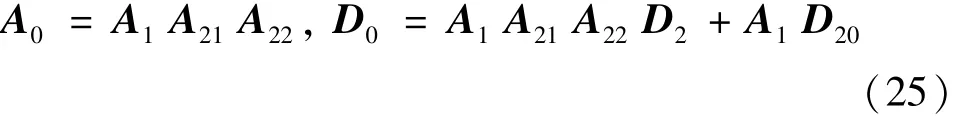
其中,D0是从初始坐标系观察到的位移,其二次导数为
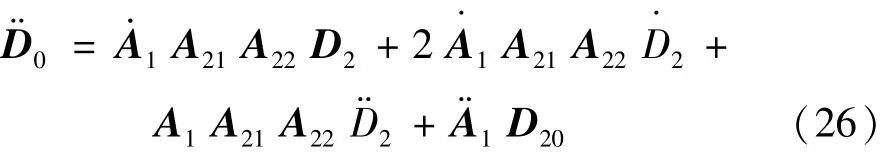
那么,加速度计感测到的加速度可以表示为

将公式(25)和(26)代入(27),可得
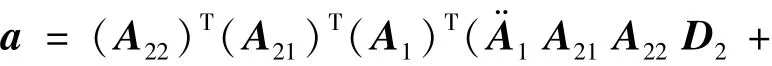
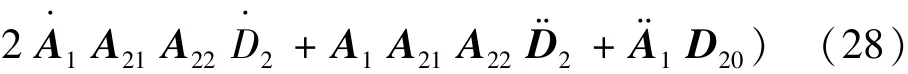
将表中的相应表达式代入到公式(28),可以求得离心-振动复合校准系统输出加速度的一般表达式为
令:
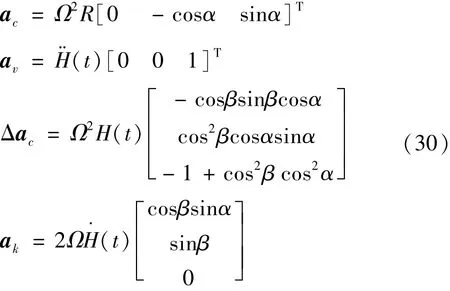
则公式(30)可写为

式中:a c为离心机输出的恒加速度,方向指向离心机转轴;a v为振动台产生的振动加速度,方向指向振动平衡位置;Δa c为因为加速度计随着振动台台面移动引起的位移变化而产生的“伪振动加速度”,方向与a c相同;a k为因为加速度计相对于离心机旋转平面运动而引起的科里奥利加速度,简称“科氏加速度”,方向与离心机转速方向和振动方向所在平面垂直,即沿着转动平面的切线方向。
2.2.2 顺臂安装和垂直安装分析
若令振动台位移的表达式为

则有
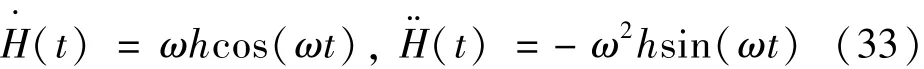
式中:(t)为振动加速度;ω为振动台的角频率;h为振动台的振幅。将公示(23)和(24)带入公式(30)得
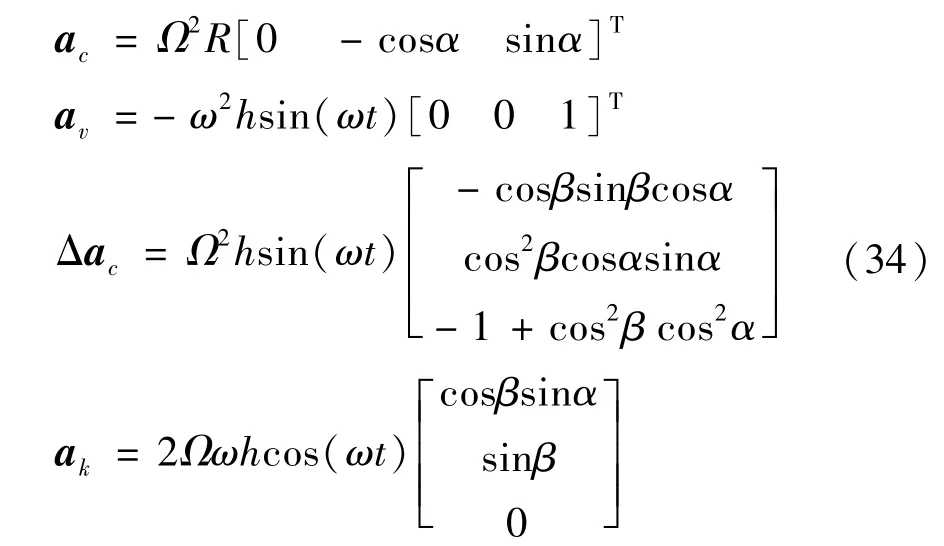
显然,除了ac以外,其他三个加速度都是与振动台相关的周期性的加速度,则公式(31)中周期性加速度施加在加速度计三个轴上的加速度分量形式,可以重写为
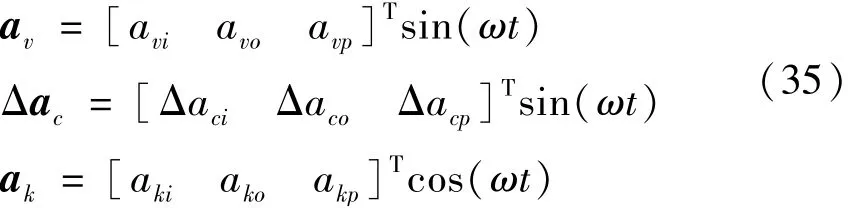
离心机产生的恒加速度与重力加速度也可以写为
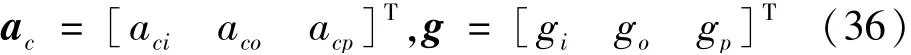
如公式(29)所示的离心-振动复合校准装置系统输出加速度的一般模型,在实际使用过程中,常用的有两种特殊模型。第一种是使得振动台振动方向与离心机旋转平面垂直,称为“垂臂振动”。令α=β=0,代入(34),得离心-振动复合校准装置产生的加速度分量为
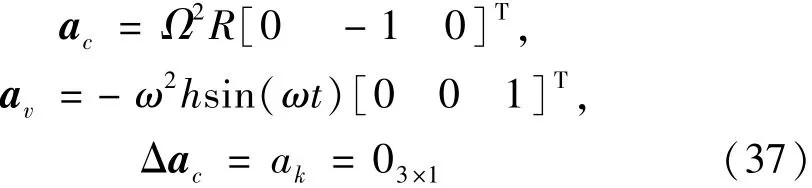
此时离心-振动复合校准装置输出的加速度可表示为
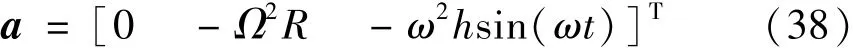
这种情况下,加速度计坐标系中,只有水平方向的恒加速度与竖直方向的振动加速度作用,不产生同一方向的复合。第二种是使得振动台振动方向与离心机旋转平面平行,称为“顺臂振动”。令α=-π/2,β=0,得到离心-振动复合校准装置产生的加速度分量为
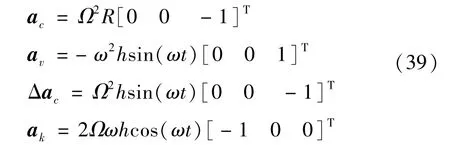
再考虑重力的影响,此时离心-振动复合校准装置输出的加速度可表示为
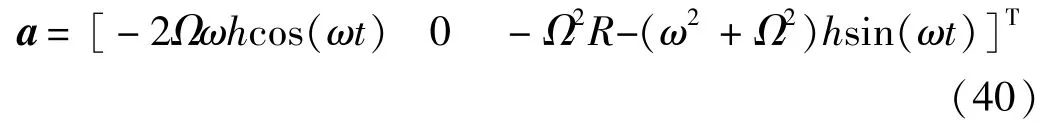
这种情况下,加速度计坐标系中,将有竖直方向的恒加速度与振动加速度组成的复合加速度,而且有明显的科氏加速度。科氏加速度垂直于离心机转速方向和振动方向组成的平面,在顺臂振动情况下,如果加速度计IA与离心力方向一致,那么科氏加速度属于横向加速度,加速度计的横向灵敏度是确定加速度计模型的重要参考。在给定横向灵敏度的前提下,横向加速度越大,显然对加速度计IA输出信号的干扰越大。
3 不确定度分析
以理想顺臂振动情况下的离心-振动系统输出加速度为例进行分析,首先给出理想的顺臂振动情况下离心-振动复合校准装置输出加速度的形式(不含重力加速度),即
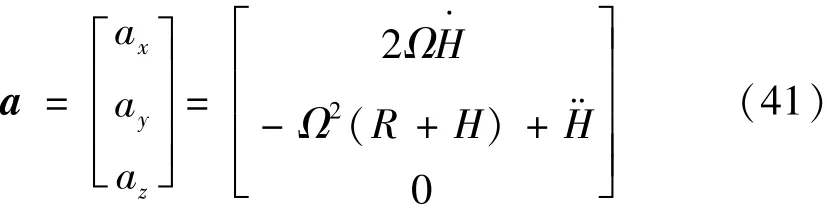
式中:Ω为离心机角速度,rad/s;R为离心机工作半径,即离心机转轴到振动台平衡位置的距离,m;H为振动台的位移,m。若令振动台位移的表达式为

式中:ω为振动台角频率,rad/s;t为时间,s。
则有
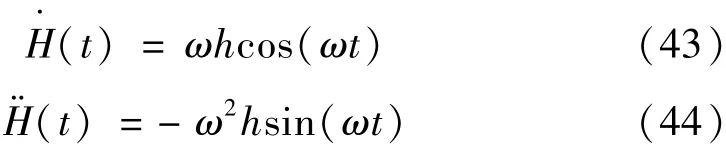
根据公式(41)和(43)
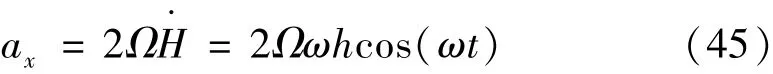
其幅度为

式中:Av=ω2h,为振动台的振动加速度幅度。则科氏加速度相对不确定度表达式可以写为
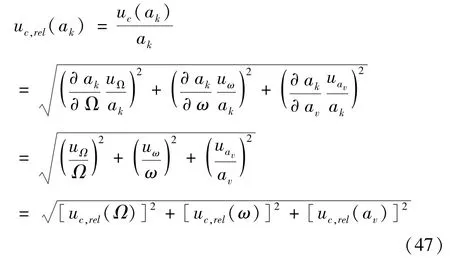
根据公式(41)和(44)

其幅度为

式中:af1=Ω2R为离心机输出的加速度;af2=ω2h为振动台输出的加速度;af3=Ω2h=Ω2av/ω是振动台在离心力场中运动运动引起的“伪振动加速度”。af的相对标准不确定度的平方等于af1、af2和af3的相对标准不确定度的平方和。离心机输出加速度的相对标准不确定度和振动台输出加速度的相对标准不确定度根据各自的校准结果给出。这里只需要分析af3的相对标准不确定度

现在,考虑以下因素对输出加速度幅度的影响:
1)标准加速度计输出电压测量引入的标准不确定度分量
使用Agilent的3458A真有效值电压表读取标准加速度计的电压输出。从检定证书得到,在测量范围10-2~10 V内,电压测量误差为0.02%,测量准确度优于读数的0.05%;估计由电压幅度测量误差引入的对测量不确定度评估的贡献值为0.05%,认为是均匀分布,有
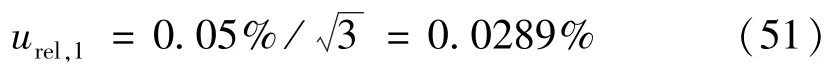
2)振动台波形失真对标准加速度计输出电压测量影响的标准不确定度
振动台产生的正弦运动中存在谐波失真,且混杂有交流噪声等其他干扰。这里将影响最大的三次谐波引入的灵敏度误差作为总谐波失真所引起的测量误差。根据GB/T 13823.3-92《振动与冲击传感器的标准方法》要求,振动台加速度波形失真da≤5%。实测160 Hz处,da=2.5%由其带给电压测量的最大相对误差为:Δda=d2a/2±da/9≈0.31%。认为是均匀分布,有:
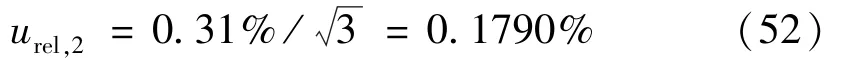
3)非理想振动对加速度计输出电压测量影响的标准不确定度
非理想振动包括横向、摇摆和弯曲振动等。离心-振动系统中,科氏加速度是主要的横向振动。这里认为横向振动影响为最大。根据横向灵敏度测试结果,可以得到加速度计最大横向灵敏度方向,使之与主振动方向平行。根据GB/T 13823.3-92要求,振动台台面中心横向加速度幅值应不大于主振方向加速度幅值的10%,标准加速度计最大横向灵敏度不大于2%。实际采用的标准加速度计的最大横向灵敏度为0.19%,实测160Hz点,台面横向振动比为5.63%。假设横向灵敏度ST和横向振动比a T未知,但是在给定范围内是矩形分布的,那么,由横向振动引入的电压测量误差最大为:Δv=STaT=1.07%,引起的相对误差为
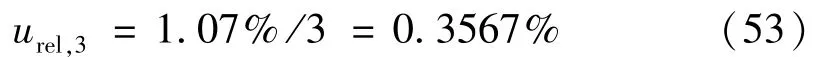
4)标准加速度计灵敏度幅值的稳定性引入的标准不确定度分量
根据统计数据,标准加速度计灵敏度的年稳定度要优于0.2%,视之为正态分布,则有
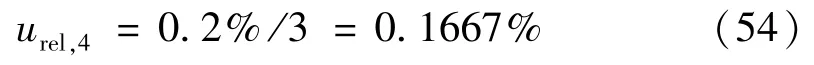
5)环境对标准加速度计灵敏度幅值的影响引入的标准不确定度分量
估计测试环境的温度、安装扭矩、工装和电缆固定等对标准加速度计灵敏度幅值的影响小于0.07%,认为是均匀分布,则有
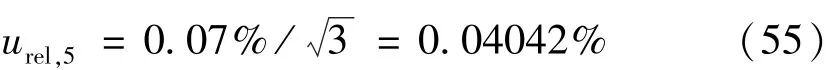
6)环境对适配放大器增益的影响引入的标准不确定度分量
测试环境对适配放大器增益的影响,一般估计不大于0.02%,看作均匀分布,则

7)振动频率测量引入的标准不确定度分量
一般采用频率计对振动信号的角频率ω进行测量。采用标准信号源HP33220A,频率准确度可达2×10-6。考虑时标准确度、触发误差、频率漂移以及测试环境的温度影响等因素,认为其对测量不确定度的影响为0.04%,且为均匀分布,因此
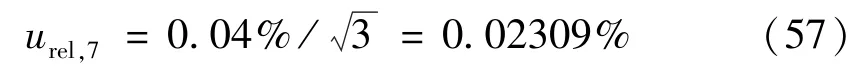
8)离心机角速度平均值测量引入的标准不确定度分量
角速度平均值误差主要是由角速度测量装置和方法决定的。这里采用定时测角法进行测量,即在给定时间内测量转过的角度。用公式表示为

则测量的相对误差可以表示为

式中:时间t的测量采用高精度晶振,时间精度可达10-7s,取Δt=1×10-7s;角度θ则通过德国海德汉公司的RON 786光栅角度编码器测量,角度误差Δθ=2″。设置定时t=0.1 s,测得转过的角度θ=36°。则角速度平均值的相对误差为
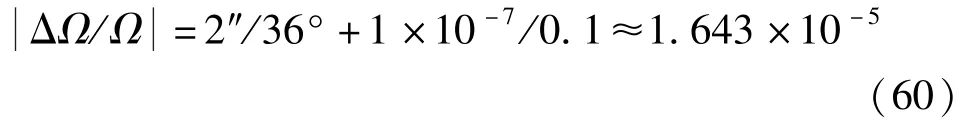
且为均匀分布,则
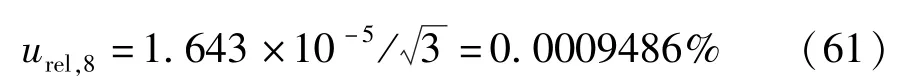
9)离心机输出加速度的标准不确定度
按照离心机的检定结果,离心机输出加速度的标准不确定度为3.431×10-5,认为是均匀分布,则

10)振动台输出加速度的标准不确定度
按照振动台的检定结果,振动台输出加速度的标准不确定度为0.78%,认为是均匀分布,则
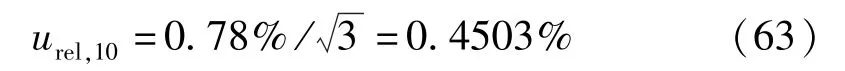
11)系统噪声的影响
所谓系统噪声,是指功率放大器不加信号时,振动台输出的电压波形。系统噪声是由电压测量系统噪声、离心机系统噪声以及其他背景噪声综合引起的。振动台输出加速度波形失真实际上包含了这类噪声的影响。因此不单独列出系统噪声引起的不确定度。
根据表3所示的不确定度分配表,计算科氏加速度幅度的相对标准不确定度为
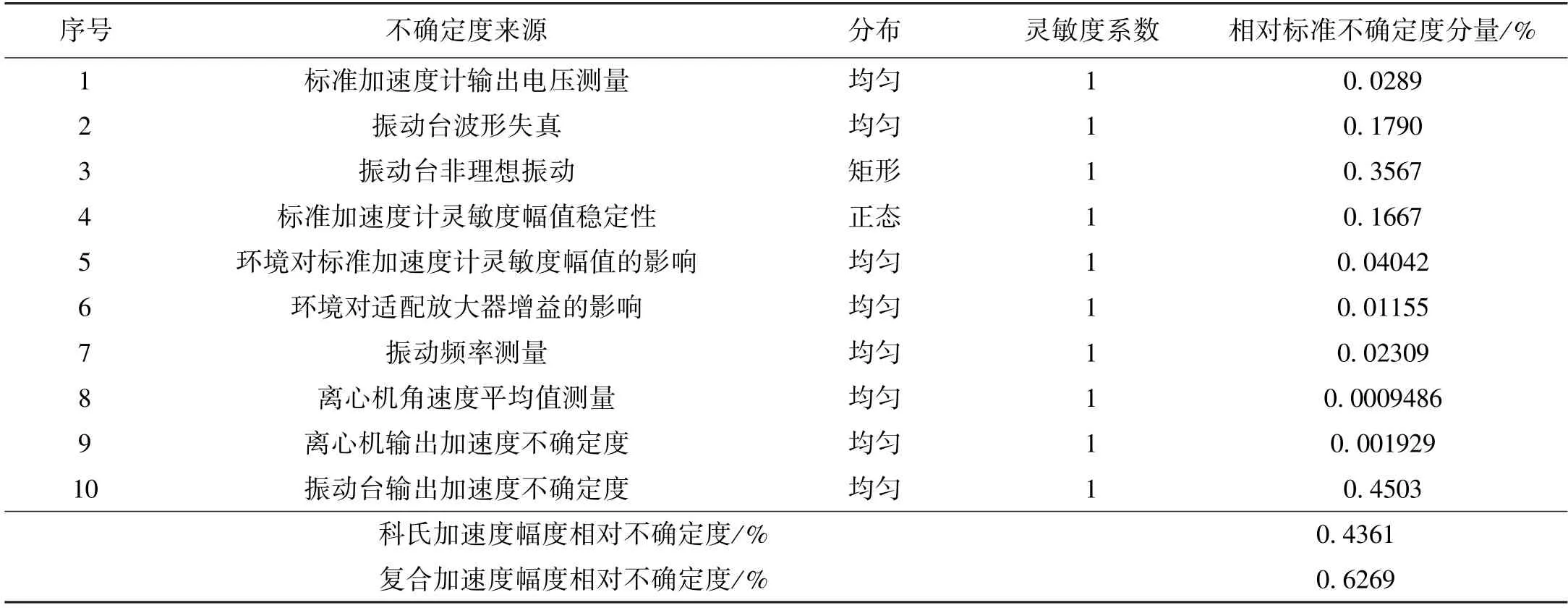
表3 不确定度分配表
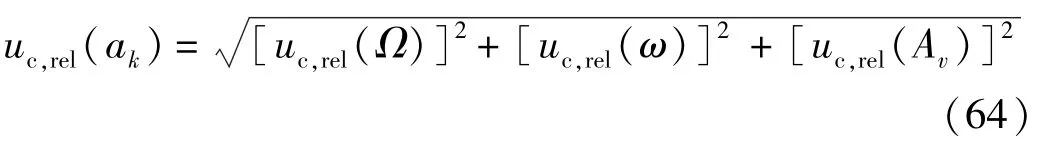
其中

而复合加速度的幅度的相对标准不确定度为

4 设备及组成
以离心机为主体,振动台安装在离心机臂(或台体)上,一般分为振动台顺臂安装和垂臂安装两种情况,即:离心加速度与振动加速度同向;离心加速度与振动加速度垂向[11-12]。
垂臂安装情况下,离心加速度与振动加速度理论上没有耦合,独立施加在加速度计上,即加速度计受到三个相互独立的加速度输入:来自离心机的离心加速度、来自振动台的振动加速度以及重力加速度。
顺臂安装情况下,由于振动台台面及台面上夹具、夹具及加速度计有相对于离心机旋转平面的运动,将产生额外的科里奥利加速度,简称“科氏加速度”。科氏加速度矢量与振动加速度矢量、离心机旋转角速度矢量相互垂直。科氏加速度与振动加速度密切联系,与离心机旋转角速度也密切联系。这种情况下,加速度计受到四个加速度输入:来自离心机的离心加速度、来自振动台的振动加速度、由于相对离心机旋转平面运动产生的科氏加速度以及重力加速度。
我所研制的“离心-振动复合校准装置”整体结构主要由离心转台、振动台、控制系统组成,如图5所示。

图5 离心-振动复合校准装置
5 实验结果
针对离心机产生的“伪振动”对校准结果的影响,本文采用独立控制的两组线圈,一组产生基础振动信号,称为“基础线圈”;另一组产生用于抵消“伪振动”的激振力,称为“补偿线圈”。如图6所示。两组线圈采用独立的激励电流接口(IN1,OUT1和IN2,OUT2),独立进行控制。在振动台台体内部设置了一只非接触式电涡流位移传感器,实时监测振动台活动部件(动圈)偏离理想平衡位置的位移,并根据该位移的变化,调整补偿线圈的激励电流,使其产生一个与实际“伪振动”相反的振动,达到补偿“伪振动”的目的。图7为本文采用的振动台及其控制系统的实物图。上位机与下位机通过无线方式通信。无线动态数据采集获得振动台动圈位置、动圈温度以及振动台台面上安装的传感器信号等数据,并发送到上位机控制中心。上位机通过实时监测振动台动圈的位置,来调节补偿线圈的电流大小和方向,实现对“伪振动”的抵消。

图6 双线圈独立控制补偿离心力示意图
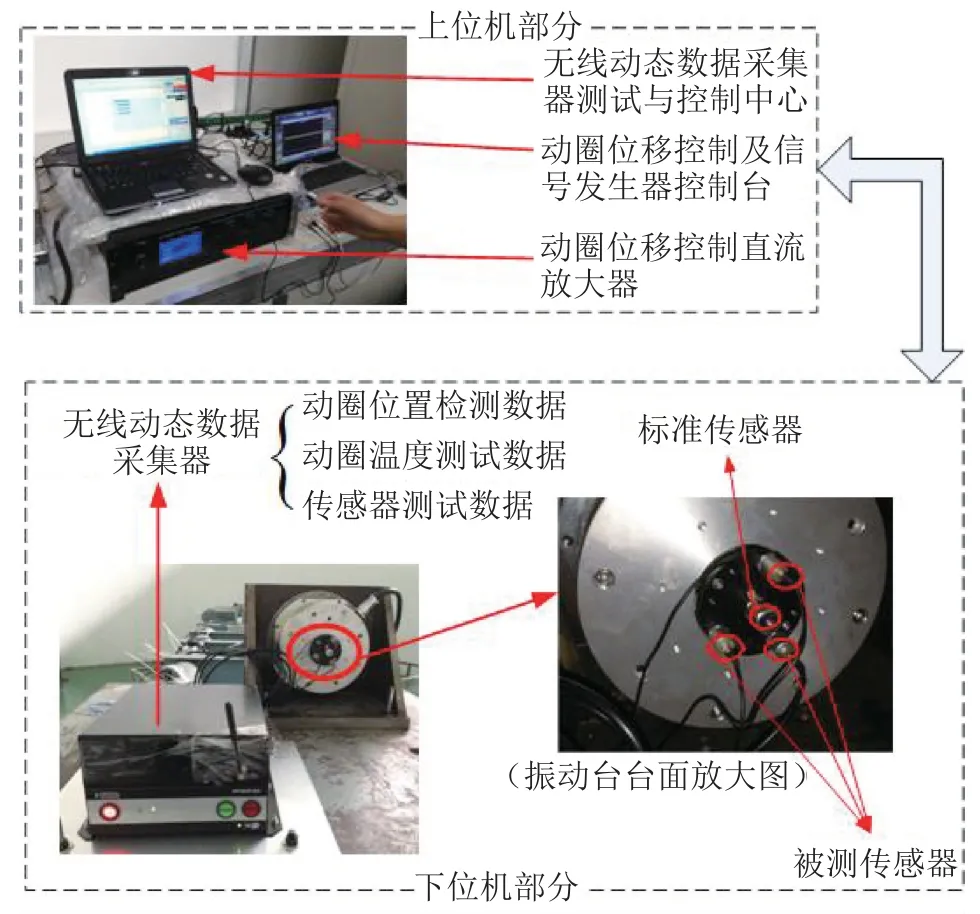
图7 电磁振动台控制系统
由于电磁控制简单实用,响应速度快,这套方案取得较为满意的实际效果。总体而言,在20~100 Hz的情况下,该方案能够很好的抵消“伪振动”影响;在100~2000 Hz情况下,这种影响还是比较明显的。图8是施加双线圈独立控制之后的振动台输出信号。图8(a)为在输入信号恒加速度20g,振动幅度20g,振动频率40 Hz下的振动台输出信号;图(b)为在输入信号恒加速度5g,振动幅度20g,振动频率40 Hz下的振动台输出信号;图8(c)为在输入信号恒加速度20g,振动幅度20g,振动频率160 Hz下的振动台输出信号。图8(a)和图8(b)的信号显示,振动台的输出信号是与设置一致的。图8(c)的信号显示,当振动频率较高时,“伪振动”影响没有得到很好的消除。相反地,补偿线圈提供了额外的激振力,施加在振动台动圈上,使得振动幅度变大。

图8 振动台输出信号
6 结论
本文对离心-振动校准装置进行了详细介绍,分别从动不平衡问题、复合方式、复合模型三个方面进行了研究。并采用数值方法对离心-振动模型误差进行计算,分析了复合环境下动不平衡的影响,讨论了在顺臂安装和垂直安装下受到的加速度大小,得出了在离心-振动复合校准装置机械结构固定的情况下,减小振动台振幅和离心机角速度,能够削弱动不平衡影响的结论。本文建立的校准装置和校准方法,能够模拟真实校准环境,具有重要的理论价值和实际意义。

