正弦波形同步采样条件的识别与判定

梁志国

(航空工业北京长城计量测试技术研究所 计量与校准技术重点实验室,北京 100095)

0 引言

同步采样一直有两种不同的含义:①针对多通道数据采集系统而言,同步采样意味着不同通道在同时采样时,其采样时刻点保持统一和一致的特征,称多通道同步采样[1-3],也称为多通道同时采样;②针对采集通道的采样间隔与被测周期信号的波形周期而言,当信号波形周期“恰好”等于采样间隔的整数倍,使得每个信号波形周期“恰好”包含整数个采样数据点,也被称为信号的同步采样[4-13]。本文后续内容,主要指信号的同步采样。

信号同步采样是对周期信号波形等间隔采样的一种特殊采样状态,通常指每一个信号波形周期“恰好”含有整数个采样点的情况。此时,采样频率是信号重复频率的整数倍。

广义的信号同步采样则是指采样序列中“恰好”含有整数个信号波形周期的情况。

同步采样是一种非常特殊且重要的测量条件,在同步采样条件下,人们很容易实现采样频率与信号重复频率之间的无误差互导。并且,信号波形及采样不完善所造成的影响趋于完整和稳定。相应地,其不确定度评定结果也趋于稳定和真实,不会由于采样不同步带来的影响而额外变化。另外,同步采样条件给周期波形采样序列带来的最大益处是其频谱分析结果没有由于采样不同步问题而带来额外的频谱泄漏,给其频谱分析、失真分析等带来极大的便利。

因而,人们千方百计地创建同步采样条件,以简化和避免后续信号分析中的问题和难度。特别是在交流电能与功率分析中,即使达不到完全的同步采样条件,也希望能获得近似同步的采样状态,以期获得更加稳定可靠的波形分析结果。否则,人们就要采取滤波、加窗等数据处理方式,以降低由于不同步造成的频谱泄漏的影响。

除了采用与被测周期信号自动同步与锁相技术的同步采样系统外,任何使用与被测周期信号不同时基的数据采集系统,若想达到完全的同步采样条件都是十分困难的。因而,人们发展了准同步采样理论方法[14-23],即采样序列包含近似整数个信号波形周期,即对于正弦波而言,包含2π·N±Δ的相位差,其中,N为正整数,而Δ为“很小”的相位差,在此条件下,通过对±Δ的补偿运算或迭代运算,可以对正弦波有效值、功率等使用累积运算获得估计值的参数,达到与同步采样条件下相接近的精度。但±Δ的精确测定也具有复杂性和难度,尤其是针对未知信号频率的情况下难度更大,故很多补偿修正类方法只能用于采样间隔和信号周期均精确已知的前提下。

尽管同步采样如此重要并被广泛研究,针对采样同步情况的定量评价方面的研究却一直较少,且多关注于同步不完善造成的误差方面[24-25],而不是同步问题本身。本文后续内容,即在正弦采样条件下以同步误差的形式,定量评价采样系统与被测信号之间的同步特性关系,以及准确估计准同步采样情况下的相位偏差±Δ。

1 测量原理及方法

1.1 基本思想

同步特性关系的实质是被测信号波形周期与均匀采样的时间间隔呈严格的整数比关系,因此,确定该比例是否为整数是同步特性分析与判定的关键,简单的周期计点法判断,无法避免±1个采样点的计数误差,因而不适用于解决该问题。

在正弦波形采样序列中,则有所不同。等间隔采样的正弦波拟合参数中,其直接拟合参数获得的数字角频率体现了采样间隔与正弦信号的比值关系,使用该参数进行同步特性分析判定,将避免周期计点法中的测量原理误差。

针对非正弦周期信号,通常更难识别其同步采样状态,此时,则可以使用滤波方式,将其谐波均滤除,只剩下基波分量,然后使用正弦拟合方式予以测量。

1.2 测量原理及数据处理方法

1.2.1 正弦波形的同步采样识别

设数据采集系统的通道采集速率为v,采样间隔Δt=1/v。通道采集数据个数为n,包含信号周期数为N个。信号周期为T,重复频率为f=1/T,信号峰值幅度为E。

给数据采集系统加载正弦波信号

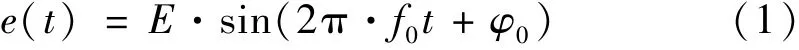
式中:e(t)为输入正弦信号的瞬时值;E为输入正弦信号的幅度;f0为输入正弦信号的频率;f0为输入正弦信号的初相位。

启动采集,得采集数据序列{xi}(i=0,…,n-1),按最小二乘法求出采集序列{xi}的拟合信号[26]

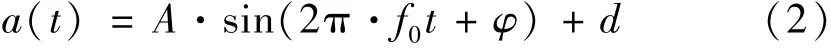
式中:a(t)为拟合信号的瞬时值;A为拟合正弦信号的幅度;f0为拟合正弦信号的频率;φ为拟合正弦信号的初相位;d为拟合信号的直流分量值。

由于采集数据序列是一些离散化的抽样值xi,其时间是离散化的ti,ti=i/v(i=0,…,n-1),式(2)可表示为

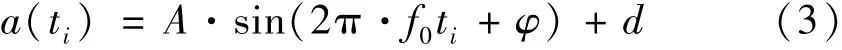
式中:ti为第i个测量点的时刻(i=0,…,n-1)。

简记为

数字角频率ω为0

则实际有效值误差ρ为

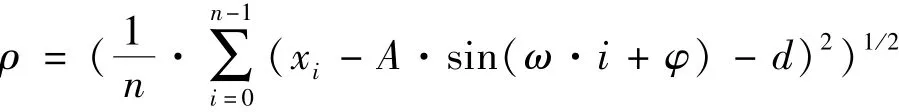
当实际有效值误差最小时,可获得式(1)的最小二乘意义下的拟合正弦波信号式(4),此时,可得数字角频率拟合结果。由此得到信号周期T与采样时间间隔Δt之比m为

令int[*]为对“*”的取整运算符,对m进行取整运算,得M为

式中:m为每个信号周期中包含的采样点数。n点采集序列中包含的信号周期数N为

1.2.2 非正弦周期波形的同步采样识别

对于非正弦类周期信号的同步采样识别,可以使用滤波器首先将其谐波尽数滤除,变成只包含基波分量的信号波形,滤波方式既可以使用一种滤波器,也可以使用多种不同滤波器进行组合滤波,带通、低通滤波均可。文献[29]所述的单频滤波器,拥有仅仅滤除谐波而对基波参数没有影响的特点,可供选择进行滤波操作。

在对非正弦类周期信号滤波完成以后,其基本上变成正弦波形,可使用1.2.1节所述方法进行同步采样特性识别,获得非正弦类周期信号的同步采样特征参数。

2 同步条件的评估

2.1 同步采样

当M=m时,每一个信号周期“恰好”包含m个采样点,此时,系统对信号处于同步采样状态,对于长度为m的倍数的采样序列而言,同步误差为0。

当N=n/m时,全序列n个采样点“恰好”包含N个信号周期,此时,系统对信号处于广义同步采样状态,对于长度为n以及其倍数长度的采样数据序列而言,同步误差为0。

2.2 非同步采样

当M≠m时,若m-M≤0.5,则定义每周期包含M个采样点,其同步误差γ为

当M≠m时,若m-M>0.5,则定义每周期包含M+1个采样点,其同步误差γ为

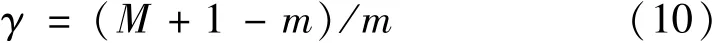
3 实验验证

3.1 正弦波形同步采样识别

用SCO232型数据采集系统,对5720A型多功能校准器进行采集,获得正弦信号波形如图1所示。A/D位数为12 bit,测量范围为-5～5 V,采集速率v=2 kSa/s,采样点数n=1800,信号峰值4.5 V,频率11 Hz。经四参数拟合得[26]:A=4459.1683 mV;ω=0.03459784 rad;φ=-138.431°;d=3.98505 mV;ρ=37.00925 mV;有效位数6.29 Bits。

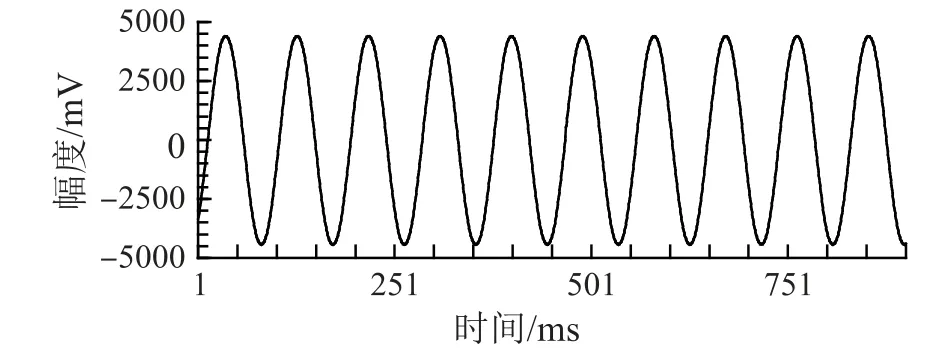
图1 实测正弦曲线波形

按式(6)计算得m=181.6063,由于m不是整数,可知此时数据采集系统对于信号的采样属于非同步采样状态。

每周期含有182个采样点,按照式(10)计算获得采样同步误差γ=0.2168%。

将采样序列进行整周期的准同步采样条件计算时,由于全序列包涵n/m=9.91155个波形周期,若以距离整数周波相差20%以内为准同步的周波数作为判据,则n/m≈10。按10个波形周期进行准同步计算时,其准同步误差为

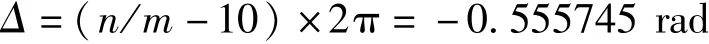
此为直接使用全部1800点进行准同步运算时的准同步误差,并未进行数据截取。

在进行数据截取后,可见序列包含9个完整波形周期,进行9周期的准同步截取后序列长度为1634点,其准同步误差为

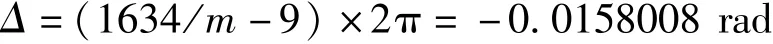
明显小了很多。

3.2 方波同步采样识别

图2为标准方波曲线波形,其幅度为4 V,频率为34 Hz,占空比为1∶1。以采样速率2048 Sa/s进行采样,采样序列长度为2000点。

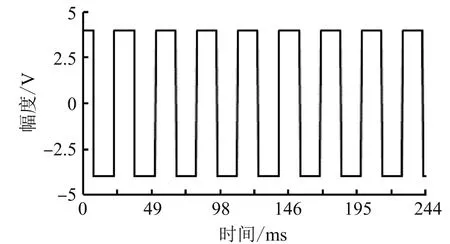
图2 标准方波曲线波形

图3为使用上述方法对图2所示波形进行滤波后获得的基波正弦曲线波形[29],使用最小二乘正弦波曲线拟合法获得其基波参数为:幅度5.1069 V,ω=0.104312872,频率为f0=34.00071 Hz,相位90.0309°,直流分量1.499317 mV,对应的总失真度TD=3.65%。

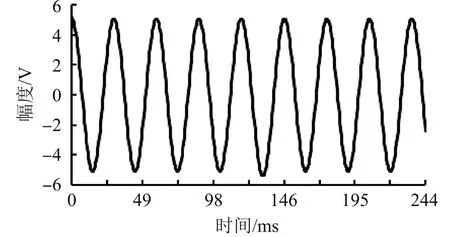
图3 标准方波滤波后基波曲线波形

按式(6)计算得m=60.2340,由于m不是整数,可知此时数据采集系统对于信号的采样属于非同步采样状态。

每周期含有60个采样点,按照式(9)计算获得采样同步误差γ=-0.39%。

3.3 锯齿波同步采样识别

图4为周期斜波曲线波形,其幅度为4 V,频率为34 Hz,上升沿与下降沿时间比为1∶4。按采样速率2048 Sa/s进行采样,采样序列长度2000点。

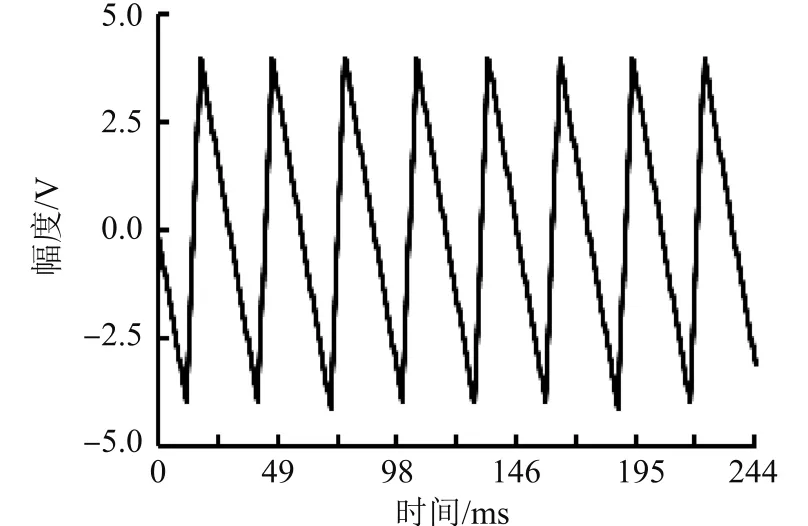
图4 周期斜波曲线波形

图5为使用上述方法对图4所示波形进行滤波后获得的基波正弦曲线波形[29],用最小二乘正弦波曲线拟合法获得其基波参数为:幅度2.98336 V,ω=0.104301152,频率为f0=33.99689 Hz,相位89.6505°,直流分量642.630 mV,对应的总失真度TD=6.19%。

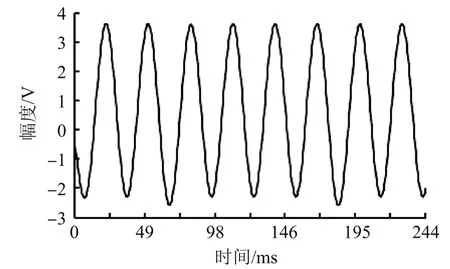
图5 周期斜波滤波后基波曲线波形

按式(6)计算得m=60.2408,由于m不是整数,可知此时数据采集系统对于信号的采样属于非同步采样状态。

每周期含有60个采样点,按照式(9)计算获得采样同步误差γ=-0.409%。

4 讨论

通过本文所述过程,可以判断采样系统对于所测周期信号是否处于同步采样状态。以正弦拟合方式获得的结果,基本上可以避免计点法±1的计点误差,获得较为确切理想的结论。通常,每个信号波形周期包含的采样点数都不是严格的整数。

若处于同步采样状态,则每个信号波形周期包含的采样点数恰好是严格的整数。此时可以计算出每一波形周期恰好包含的采样点数。从而进行采样序列长度的选定,进而使用一系列简捷有效的方法进行其它测量处理。

若处于非同步采样状态,可按照同步误差最小化原则定量判定每个波形周期近似包含的采样点数,并给出同步误差的定量评价结果。

特别是,对于准同步采样方法而言,其多周波准同步误差Δ可以定量给出,以利于有效利用补偿修正类准同步采样方法进行部分波形参数估计,为同步测量和准同步测量方法的应用创造了先期技术条件。

本文所述方法的不足之处是,它属于同步采样条件的估计,采样速率“恰好”是信号频率的整数倍的条件较难实现,由于测量误差和不确定度因素,对于真正的同步采样,也可能产生误判[27-28]。有关问题的解决,需要后续的深入研究。

5 结束语

本文针对正弦信号波形数据采集过程中常见的同步采集的辨识与判定,以及同步误差的定义和估算,本文进行了细致研究,获得了确切可用的方法和结论,本文所述方法可用于电能、电功率等电力行业的正弦基础参量的测量、计量和校准中,有广泛的应用空间。

针对非正弦类周期信号的同步采样问题,可借助于单频滤波技术予以实现,从而使本文所述方法拓展到更为广阔的应用领域,使其具有更大的意义和价值。