铜期货套期保值比率模型的评价
汤振宇
(江西财经大学 信息管理学院,江西 南昌 330013)
1 引言
铜作为日常生活中不可或缺的一种金属元素,广泛运用在电线电缆和电气、电子元件等生产过程中。铜的价格波动历来对相关企业经济业绩产生较大幅度的影响。2020年以来,受到全球新冠疫情的影响,很多国家铜矿产量急剧下降。受影响最大的为秘鲁,其铜矿产量比上一年度下降14.5%。全球铜供应量减少了25.7万t。铜现货价格也由2020年初的49033元/t,涨至年末的58303元/t,涨幅高达18.91%。伴随着我国持续深化供给侧改革,淘汰落后的铜冶炼产能,产业结构进一步优化,这将使得我国铜价愈发受到国内外市场需求端的影响。因此,如何规避铜价波动给相关行业或企业带来的不利冲击,已经成为学界和企业共同关注的焦点。
套期保值是指市场参与者通过交易期货合约来防范现货市场的价格风险,以期望在未来某一时刻,能够通过期货市场上的盈利,来抵补现货市场上铜的价格变动带来的损失。铜期货合约最早可以追溯到1877年伦敦金属交易所成立,是该交易所内最早挂牌的期货交易品种之一。我国首个铜期货也于1993年在上海推出。套期保值是期货市场的基本作用之一,货合约最早可以追溯到1877年伦敦金属交易所成立,是该交易所内最早挂牌的期货交易品种之一。我国首个铜期货也于1993年在上海推出。套期保值是期货市场的基本作用之一,也是期货市场产生和发展壮大的重要源泉。铜期货合约也成为铜冶炼、加工等相关企业规避价格变动风险的重要工具。历经近30年的发展,伴随着我国经济实力的不断提高,期货市场也取得了辉煌的成就,全球铜期货市场逐步形成了伦敦、纽约、上海三足鼎立的格局。仅2021年3月,上海期货交易所铜期货成交量就已经接近800万手,同比增长56.49%。但是,我国期货市场还存在一些不足,比如投资者结构不够完善。我国期货市场投资者一部分为“散户”投机套利活动,相关企业的套期保值意识仍然较弱[1-2]。部分期货公司业务能力不强,交易品种的风险对冲能力不足,导致部分企业即使采用了期货对冲风险,或多或少仍会受到价格波动的影响。2020年11月,习总书记在浦东开发开放30周年大会上的讲话中强调, 要完善金融市场体系,建设国际金融资产交易平台,提升重要大宗商品的价格影响力,更好服务和引领实体经济发展。因此,研究期货合约套期保值比率,具有非常重要的理论和现实价值。
2 文献综述
商品期货合约的套期保值一直是近几十年来的研究热点之一。上世纪60年代初期,沃金最先提出现代套期保值思想。该理论的实质是把套期保值看成同时在期货市场和现货市场中操作,即交易者在现货市场上买入或卖出商品的同时,在期货市场上卖出或买入对应数量的期货交易合约,以此来规避现货市场上价格波动给交易者带来的风险损失。与此同时面临的问题是,期货市场和现货市场并非是完全同步的,由此产生了基差风险。为了更好地说明潜在的基差风险,结合基差的定义,即基差=现货价格-期货价格,得出铜基差的时间序列。本文根据2020年日度交易数据计算了铜基差的时间序列并绘制走势图。
从图1明显看出,我国铜期货市场大多时候都存在一定的基差风险。即在现实的期货市场中,完美的套期保值通常是不存在的。更多的套期保值是不完美的,即无法完全消除价格风险。因此可能存在一个最优套期保值比率,使得风险最小化[3-4]。

图1 铜基差走势图
由于风险度量的方法和效用函数不尽相同,学界提出了很多种潜在模型进行研究。Ederington(1979)采用普通最小二乘法评估套期保值的效率,Marsh all etc.(1993)则认为传统的最小二乘法进行最优套期保值比率的计算会受到随机误差项的影响。为了更好地避免计算的误差,提出采用向量自回归模型(VAR)估计套期保值比率[5]。
上述模型将经典的统计学方法运用于研究金融时间序列,这种方法虽然是有效的,但是却损失了有价值的长期信息。20世纪80年代越来越多的学者参与期货市场的研究,研究者开始从多个角度研究最优套期保值比率的问题,并提出了相应的评价体系和对策建议。Granger(1986)最早提出了误差修正模型(ECM),Sowell(1992)和Cheung、Lai(1993)在此基础上进一步考虑了金融时间序列间的协整关系。Lien、Tse(1999)首次提出考虑到资产价格表现为波动的聚集性。Baillie和Myer(1986)提出了GARCH类模型计算最优套期保值比率,该模型被认为能够较好的识别期货和现货市场的价格序列中普遍存在的异方差性[6]。
目前,学术界针对期货合约套期保值率最优测算模型尚未达成一致的见解。不同商品和期货品种可能适合采用不同的套期保值模型进行测算。基于此,本文以铜为例,深入探究上海期货交易所铜期货合约套期保值率的最佳测算模型。研究内容具有一定的理论价值和现实意义,有助于铜相关企业利用衍生工具规避价格波动带来的风险,让金融市场更好地服务和引领实体经济发展。
3 研究方法
3.1 普通最小二乘法(OLS)
Ederington(1979)将20世纪60年代的套期保值理论和方法应用到金融期货市场,并提出了套期保值有效程度的计量指标[7]。利用期货收益率与现货收益率进行普通最小二乘法回归,具体模型见式1所示。

其中,RSt表示t时刻现货价格,RFt表示t时刻期货价格,β为最优套期保值比率,θt为随机误差项。采用普通最小二乘法回归(OLS)进行分析.普通最小二乘法回归要求所选择的回归模型应该使得所有的观测值的平方和达到最小.通常而言,采用残差平方和损失函数进行定义。
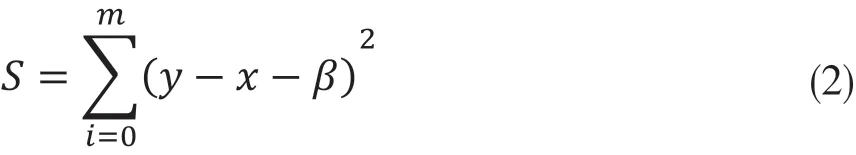
3.2 自向量回归(VAR)
套期保值效果的好坏很大程度上取决于所测算的套期保值比率是否精确,归根到底,在于其在套期保值时所使用的模型。传统OLS回归模型并没有考虑残差自相关的存在,有时可能无法准确定义和度量金融风险。为了解决这一突出问题,G30集团于1993年提出了VAR进行风险测度,其解释变量是被解释变量的滞后变量。后随着VAR方法不断的完善,已广泛运用于套期保值。VAR作为一种测算资产组合风险和收益的有效工具,目前已被广泛用于套期保值的研究[8]。
3.3 误差修正模型(ECM)
误差修正模型较以住模型不同的是,该模型考虑了两个时间序列具有的协整关系。协整关系的发现,对于时间序列的研究有了很大的飞跃。误差修正模型考虑了两个时间序列之间存在潜在的长期关系,即现货价格时间序列和期货价格时间序列的非平稳性、长期均衡、短期动态等因素,因此任何短期偏离都会被模型修正。因而计算得出的最佳套期比为一固定的常数,不随时间变化[9]。
3.4 广义自回归条件异方差(GARCH)
在离散的时间框架下,广义自回归条件异方差(GARCH)模型,被认为是目前弥补传统模型缺陷的最具竞争力的模型之一。GARCH模型假定了收益的方差服从一个可预测的过程,该模型考虑了历史和现在的数据[10]。本文选用GARCH(p,q)类模型来进行参数估计,并依照AIC和SC的信息准则要求,通过反复的比较,最终选择GARCH(1,1)模型,如式3~式5所示。
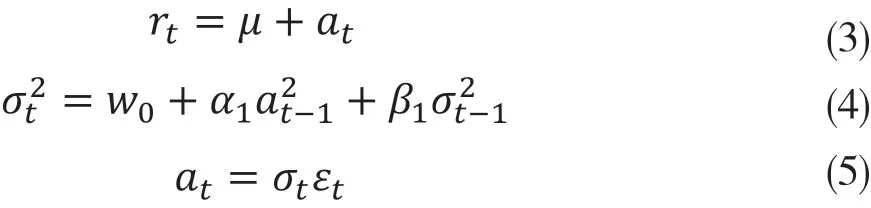
其中,εt为随机扰动项,其服从于均值为0,方差为1的正态分布。a2t-1称为ARCH项;σ2t-1为GARCH项;w0表示常数项;rt表示均值;μ、w0、α1和β1即为本文需要估计的参数。
4 数据描述及实证检验
4.1 数据描述
为了研究铜期货合约套期保值的最优策略,本文选取上海期货交易所铜期货合约(CUF)结算价格和长江有色金属市场的现货铜(CUS)结算价格的日度交易数据作为研究的对象。考虑到GARCH模型所使用的时间序列必须有一定的时间跨度,如果选取较短的套期保值时间,可能会产生较大的误差。因此,基于数据的可得性,本文选取2017年1月3日至2021年3月31日的1032个交易日的样本数据作为研究对象,并根据上文所述模型计算对应的套期保值比率。具体数据描述性统计间表1所示。所有数据均来源于Wind金融数据库。

表1 描述性统计
4.2 数据处理
在评估最优套期保值率时,首先应当计算该套期保值组合的收益率。目前,期货市场和现货市场的日收益率可以采用算术收益率和对数收益率表示。本文采用对数收益率衡量二者的收益率。因为本文需要考察单一投资品在T期内的表现,对数收益率因为其具备可加性,因此可以精准反映该投资品的真实收益率。本文采用的具体计算方法如式(6)和式(7)所示。
铜期货市场上t时刻的收益率:

铜现货市场上t时刻的收益率:

4.3 平稳性检验
由于本文所选取的时间序列样本超过1000个,为了确保时间序列的平稳性,避免潜在的伪回归导致得出错误的结论,本文首先对实验样本数据中的现货价格时间序列(St)、期货价格时间序列(Ft)、现货价格一阶差分(ΔSt)和期货价格的一阶差分(ΔFt)的时间序列进行DF和ADF单位根检验,检验结果如表2所示。
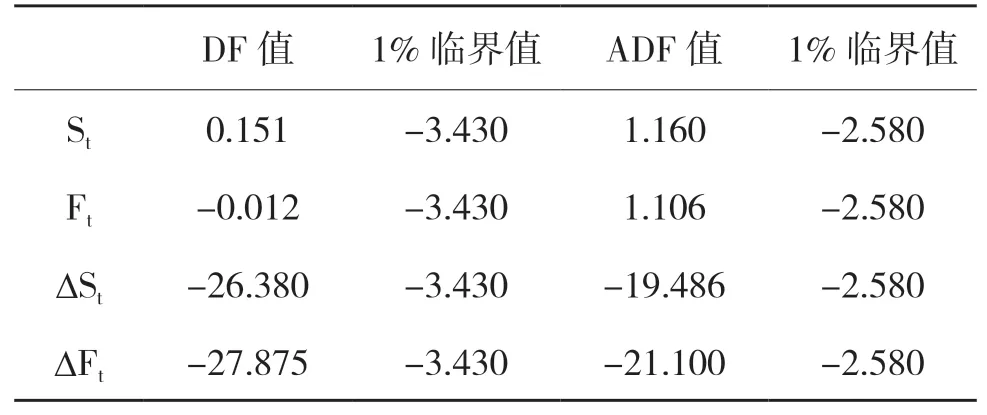
表2 时间序列平稳性检验
从表中可以看出,无论从DF检验来看,还是ADF检验来看,对应的统计量的绝对值都小于1%的临界值,即现货价格时间序列(St)和期货价格时间序列(Ft)都是非平稳时间序列。而对于现货价格一阶差分的时间序列(ΔSt)和期货价格的一阶差分的时间序列(ΔFt),从表中我们看出,对应的统计量的绝对值均显著大于1%的临界值,即二者是平稳的时间序列。
4.4 模型估计结果
根据上文所叙述的四种测算套期保值比率的方法,本文进行实证检验。在使用普通最小二乘法和误差修正模型测算最优套期保值比率的时候,将铜期货的对数收益率作为解释变量,铜现货的对数收益率作为被解释变量,以此来得到最优套期保值比率。其中,误差修正模型与普通最小二乘法不同的是,它增加了误差修正项(本文用θt-1表示)。由于现货价格一阶差分和期货价格一阶差分的时间序列研究通过了平稳性检验,因此可以使用VAR模型和GARCH模型计算最优套期保值比例。具体实证结果如表3所示。
从 表3可 以 看 出,OLS模 型、VAR模 型、ECM模型和GARCH模型的套期保值比率分别是0.818、0.799、0.851和0.850。进一步考虑调整的R平方,四个模型分别为0.779、0.965、0.951和0.801。由此可见,ECM模型和VAR模型在这方面的测算结果更加可靠,由此得到的套期保值比率可以更加有效地减少现货头寸暴露带来的风险,即通过误差修正模型和VAR模型,可以更好地测算最优套期保值比率,从而有效利用期货头寸来回避现货市场上价格波动的风险。综合来看,ECM模型在测算最优套期保值方面具有显著的优势,但是其内在的过程繁琐、不能完全规避风险等缺陷,也使得学术界不断提出新的模型来改进该模型。例如,学术界相继提出了ECM-GARCH模型等,这些模型目前仍在理论研究阶段,对于实际市场的作用仍然有待进一步考察。也正是考虑到ECM模型的缺陷,目前也有相关行业采用OLS模型进行最优套期保值比率的测算。该方法虽然没有ECM模型的结果精准,但是其便捷性、可操作性,使得实际生活中也备受偏爱。
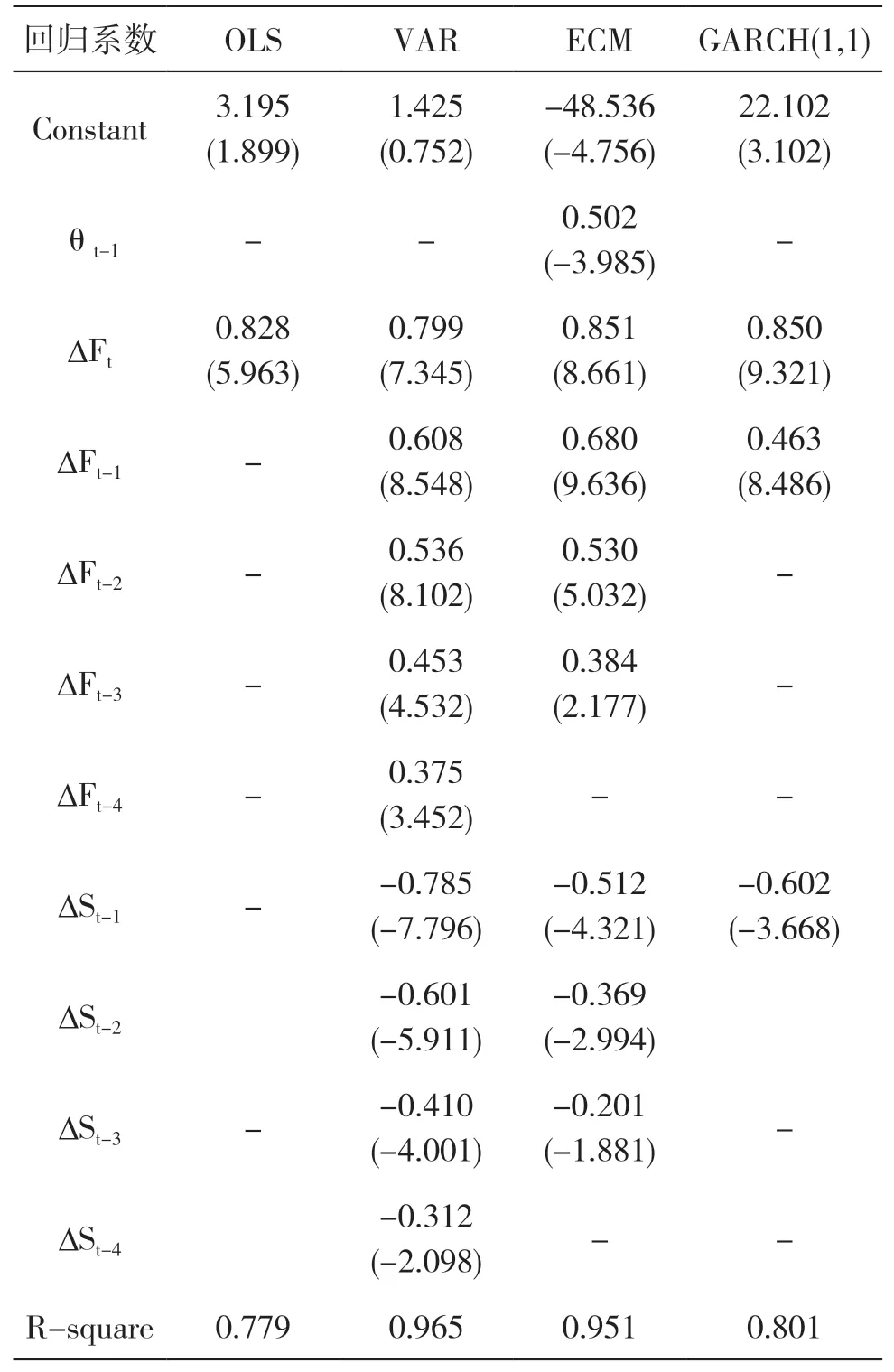
表3 模型估计结果
4.5 套期保值有效性检验
为了进一步研究铜期货交易的对冲,参考学术界做法,本文采用套期保值的有效性检验。即使用对冲后收益方差的减少程度比上不使用对冲的情况下的收益方差。由此得到套期保值有效性衡量指标H,具体见式8所示。
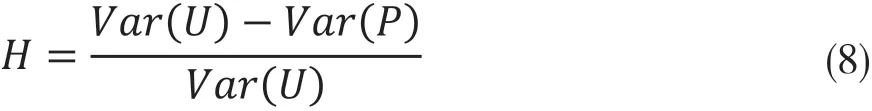
其中,Var(U)表示未参与套期保值时的收益方差,Var(P) 表示参与套期保值时的收益方差。为了便于进行对比分析,本文将上文中的1032个样本分成两份,其中包括516个样本1数据,以及516个样本2数据。计算结果如表4所示。

表4 套期保值有效性检验
从表4可以看出,ECM模型下套期保值有效率最高,而传统的不考虑时间序列间协整关系的OLS模型和VAR模型则套期保值有效率偏低。因此我们可以得出结论,如果忽略两个时间序列间的协整关系,则模型测算出的套期保值比率与实际会有一定差距。
5 结论
本文利用上海期货交易所内的铜期货合约价格与对应的铜现货价格的时间序列,研究了相应的套期保值比率测算模型。我们发现,相对于传统的OLS模型和VAR模型,考虑了两个时间序列间协整关系的ECM模型和VAR模型能够更好地测算最优套期保值。其中,ECM模型的最优套期保值比率,调整的R平方以及套期保值的有效性均在一定程度上优于其他模型。可见,ECM模型相对于其他模型有一定的优化改善。但是在实际运用中,传统的普通最小二乘法以期原理简单,操作性强而受到一部分人的青睐。而新兴模型,诸如ECMGARCH等也发展迅猛,为套期保值提供了更加科学的理论支撑。它在ECM模型的基础上,进一步将静态套期保值比率,优化为动态套期保值比率,但是在实际运用中仍不成熟。相信,随着套期保值研究的不断深入,未来将有更好的模型来解决套期保值问题,有利于相关企业减少经营风险,更好服务实体经济的发展。

