高速铁路大跨度混合梁斜拉桥-无砟轨道隔离层减振效果试验研究

罗天靖,郑纬奇,盛兴旺,李 辉

(1.中铁工程设计咨询集团有限公司,北京 100055； 2.中南大学土木工程学院,长沙 410075)

1 概述

高速铁路带来的振动问题日渐突出，由于速度快，引起的高频振动会产生大量的噪声污染，并通过桥梁结构传递至地基与附近建筑物，会显著影响周围医院、高校以及科研单位等精密仪器设备，干扰周围居民的正常生活、工作和学习，严重时甚至导致建筑物开裂[1]。

国内已有团队针对高速铁路无砟轨道在路基、箱梁、隧道上的振动特性[2-7]进行了研究，然而针对大跨度桥梁上，以及基于减振轨道结构的研究仍有不足。基于赣江桥的足尺节段模型，通过锤击试验研究了大跨度桥梁上，不同隔离层下轨道与桥面间的振动传递情况与时-频衰减特征。

新建铁路南昌至赣州客运专线赣江特大桥是昌吉赣客运专线跨越赣江的控制性工程。全桥长2155.440 m，分孔布置为：22×32 m简支梁+(35+40+60+300+60+40+35) m结合梁+4×32 m简支梁+2×24 m简支梁+11×32 m简支梁。赣江特大桥跨赣江主跨采用双塔斜拉桥、主梁为结合梁(图1)，位于直线、平坡地段，该桥是目前高速铁路上跨度最长的混合梁斜拉桥，并且首次在高速铁路斜拉桥上铺设无砟轨道，是世界上首座时速在350 km、300 m大跨度斜拉桥上铺设无砟轨道的混合梁斜拉桥[8-12]。

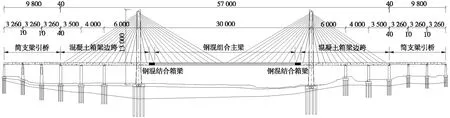
图1 赣江特大桥主桥立面布置(单位：cm)

2 振动锤击试验

为了研究大跨度斜拉桥与无砟轨道的适应性，对赣江桥进行足尺节段模型试验。考虑试验室条件等因素，节段模型简化为一跨连续带悬臂结构，使用刚性支点(支墩A)与弹性支点(支墩C)模拟斜拉索的弹性效应，等效跨中节段的大挠曲变形状态。跨度布置为6.0 m(悬臂段)+12.0 m+6.0 m(悬臂段)，共计24 m，试验梁高为1.5 m，断面与斜拉桥钢箱主梁大小相同(不考虑风嘴)，并在该模型上开展落锤振动等试验[13]。节段模型布置见图2，激振点示意见图3。

图2 节段模型布置(单位：m)

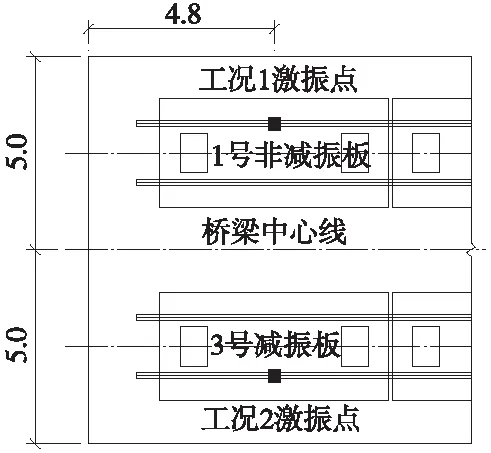
图3 激振点示意(单位：m)

通过力锤激振试验，通过加速度传感器获取钢轨、不同类型轨道板、底座板与桥面板的振动时程数据，研究节段模型中轨道系统与桥梁系统的振动加速度衰减与变化，进而研究节段模型系统振动传递规律与不同隔振垫层的减振效果。其中减振板采用新型橡胶隔离层[14]，非减振板采用土工布隔离层。为了达到宽频带高振幅的激振效果，选择铝制锤头进行试验，设置两种激振工况。

工况1：非减振板中央处对外侧钢轨激振；

工况2：减振板中央处对外侧钢轨激振；

两种工况分别用于研究振动通过不同隔离层轨道板从上往下的竖向传递情况，与振动沿钢轨在不同隔离层轨道板上的纵向传递情况，测点汇总如表1所示。

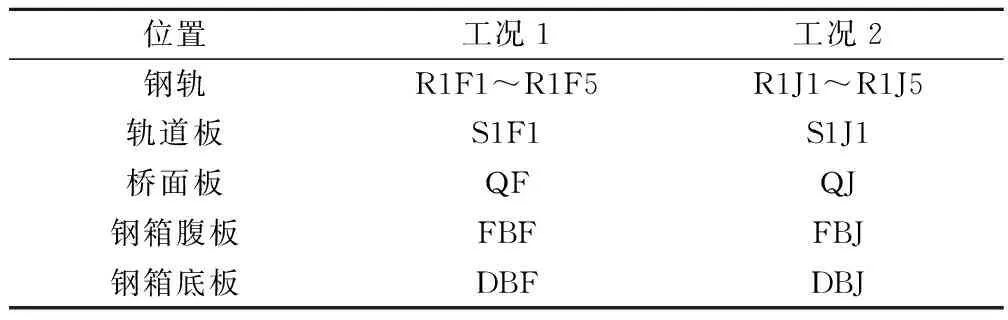
表1 测点汇总

测点布置原则：R1F(J)1至R1F(J)5距离激振点由近到远各间距1.5 m，沿纵向设置在钢轨上表面。S1F(J)1设置在紧挨R1F(J)1相同纵向位置处轨道板表面上，Q1F(J)设置在紧挨S1F(J)1相同纵向位置处桥面板表面上，FBF(J)设置在紧挨Q1F(J)相同纵向位置处钢箱梁腹板外侧中央，DBF(J)设置在紧挨FBF(J)相纵向位置处钢箱梁底板底侧。

3 不同隔离层振动的时-频分析

由于工况1、工况2的试验数据较多，且激振轨道的工况规律相似，限于篇幅本文仅选取各工况的典型测点进行分析，时程数据进行频域展开则能获得详细的频域变化情况，再对级差数据进行Savitzky-Golay滤波(最小二乘平滑滤波)拟合，可以在离散数据中得到统计上的衰减规律；而对时程数据叠加小波变换，可以得到时-频域三维变化情况，揭示振动的各频段组成、沿时间轴的变化情况[15-20]，研究振动在各板型的传递规律与减振效果。

3.1 钢轨纵向传递时-频分析

取工况1非减振板被激振钢轨测点R1F1、R1F3、R1F5，工况2减振板被激振钢轨测点R1J1、R1J3、R1J5时程数据进行FFT傅里叶变换得到频域图，并对R1F5、R1J5的时程数据叠加小波变换，得到三维时-频域图(Z轴为加速度)。因钢轨振动波形比较相似，仅展示该三测点的图形。如图4～图6所示。

图4 R1F(J)1测点频域图5 R1F(J)3测点频域图6 R1F(J)5测点频域

由图4～图6可知：(1)R1F1处钢轨在2.5～3 kHz频段幅值最大达到3 m/s2；R1J1处钢轨则集中在2～2.5 kHz频段，幅值达到5.5 m/s2。(2)振动传到R1F3后，激振频段保持在2.5～3 kHz，幅值减小至1.5 m/s2；R1J3处激振频段漂移至2.5 kHz，幅值大幅减小为0.5 m/s2，与其他频段幅值接近。(3)振动传递到R1F5后，发生轻微漂移至2.8 kHz，峰值继续下降至0.7 m/s2，下降趋势与距离呈正相关；R1J5处激振频段继续向高频漂移至3 kHz，峰值进一步下降为0.7 m/s2，与R1F5接近。

由图7、图8可知：R1F5测点在2.6～2.8 kHz频段的激振时间较长，达到0.05 s，在低频段500 Hz以下的激振时间更长，达到0.08 s；R1J5处测点在3 kHz频段的激振时间较长，达到0.05 s，同样在低频段500 Hz以下的激振时间达到0.08 s。

由图9的R1F(J)1->R1F(J)3振动级差对比可知，振动从的R1F(J)1传递至R1F(J)3：(1)在低频段(0～1.5 kHz)下，减振板与非减振板衰减趋势基本一致，可认为隔离层对低频振动的衰减无明显影响。(2)对于中频段2～3 kHz的振动，减振板衰减最大，最高处达到28 dB，非减振板只有11 dB，相差17 dB。(3)3 kHz以上高频段减振板与非减振板仅相差5 dB。

3.2 钢轨-轨道板-桥面-钢箱梁竖向传递时-频分析

取工况1、工况2测点S1F(J)1、Q1F(J)、FBF(J)、DBF(J)时程数据转化为频域、时-频域、级差分析，与上文处理方法相同。其中FBF(J)、DBF(J)结果相似，故只展示FBF(J)结果。

由图10～图12可知：(1)S1F1处，轨道板混凝土被宽幅激振，振动幅值最大不超过0.04 m/s2；S1J1处激振规律与S1F1相似，但在2 kHz处出现明显峰值，达到0.08 m/s2。(2)振动传递至Q1F处，在2 kHz处出现峰值，幅值下降至0.006 m/s2；Q1J处在500 Hz以下出现峰值，最高仅0.001 m/s2，且在2 kHz处无峰值，曲线衰减明显。(3)振动传递至FBF处，规律与Q1F处相似，但峰值放大至0.04 m/s2；FBJ处振动规律与FBF相似，2kHz处出现峰值，整体幅值呈放大趋势，但最高仅为0.005 m/s2。

由图13、图14可知：Q1F处振动集中在2 kHz处，峰值振动仅维持0.004 s，而Q1J处振动在整个频段上长时间持续，2 kHz以上频段在0.15s左右，低频段0～500 Hz达0.3 s以上。

由图15的S1F(J)1->Q1F(J)振动级差对比可知，振动从S1F(J)1传递至Q1F(J)：(1)在中低频段0～3 kHz范围内，非减振板级差为20～40 dB，减振板为40～60 dB，平均相差20 dB，最高点相差40 dB，减振效果明显。(2)在3～5 kHz处减振板级差为30～40 dB，非减振板为25～35 dB，平均相差5 dB。

图7 R1F5测点时-频域图8 R1J5测点时-频域图9 R1F(J)1->R1F(J)3级差对比图10 S1F(J)1测点频域图11 Q1F(J)测点频域图12 FBF(J)测点频域图13 Q1F测点时-频域图14 Q1J测点时-频域图15 S1F(J)1->Q1F(J)级差对比

4 结论

(1)从钢轨的纵向传递规律可知，钢轨的激振频率集中在2～3 kHz，振动在传递中会向高频段漂移，非减振板从2.7 kHz漂移至2.8 kHz，减振板从2.5 kHz漂移至3.0 kHz。减振板的漂移现象更为明显；减振板在2～3 kHz频段衰减明显，最大相差28 dB。

(2)从钢轨的纵向传递规律可知，在2～3 kHz频段处振动从峰值下降至最低值的过程中，非减振板钢轨振动衰减与距离呈正相关，而减振板在很近距离内衰减至最低量级。

(3)从钢轨-钢箱梁的竖向传递规律可知，两种板型轨道板处的激振频段均变为宽幅0～3 kHz，幅值接近，在2 kHz处出现峰值，传递到钢箱梁后振动均被放大。

(4)从钢轨-钢箱梁的竖向传递规律可知，两种板型桥面板处的振动衰减差异明显，非减振板振动集中在0～500 Hz、2 kHz频段处，减振板则集中在0～500 Hz频段处；减振板在0～3 kHz频段处的级差平均比非减振板高20 dB，衰减效果明显。