多参数n阶α次积分C半群的生成定理

毕 伟

(延安大学 学术期刊中心，陕西 延安 716000)

在算子半群理论[1]中，无穷小生成元及其性质是各类算子半群研究的重要内容。文献[2-3]给出了双参数C半群和双参数有界算子C群的生成元及性质；文献[4-6]讨论了双参数C半群和双参数n阶α次积分C半群的Yosida逼近等问题；文献[7-9]给出了两类多参数半群的定义及其性质。基于上述文献，本文给出多参数n阶α次积分C半群的无穷小生成元的定义，研究多参数n阶α次积分C半群无穷小生成元的一些基本性质，即生成定理，从而丰富了多参数半群的理论。

1 基本概念

设N为自然数集，X为无限维的复Banach空间，B(X)是X上有界线性算子全体所成的Banach代数，D(A)为线性算子A的定义域，规定所有n,m∈N，α≥0。

定义1[8]设n∈N，α≥0，{T(t1,t2,…,tm)}t1，t2，…，tm≥0⊂B(X)强连续，若存在线性算子A=(A1,A2,…,Am)使得(1)～(3)式成立：

(1)∀x∈X,t1，t2，…，tm≥0，

JnT(t1，t2，…，tm)x∈D(A)，

AJnT(t1，t2，…，tm)x；

(2)∀x∈D(A)，t1，t2，…，tm≥0，

JnT(t1，t2，…，tm)Ax；

(3)CT(t1，t2，…，tm)=

T(t1,0，…,0)T(0,t2,…,0)…T(0,0,…,tm)。

定义2 多参数n阶α次积分C半群{T(t1，t2，…，tm)}t1，t2，…，tm≥0的无穷小生成元记为线性算子A=(A1,A2,…,Am)，A=(A1,A2,…,Am)为C-1与T(t1，t2，…，tm)在(0，0，…，0)处的微分的积，其中{T(t1,0,…,0)}t1≥0，…，{T(0，0，…，tm)}tm≥0为多个单参数n阶α次积分C半群，而它们由线性算子A1,…,Am生成，即

x∈D(A)；

D(A)=

2 主要结果

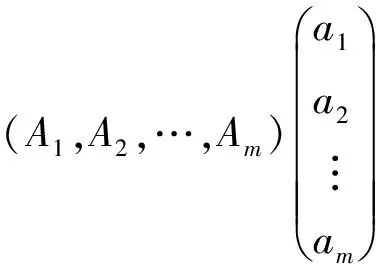
证明设{T(t1,t2,…,tm)}t1,t2,…,tm≥0是多参数n阶α次积分C半群，那么{T(t1,0,…,0)}t1≥0，{T(0,t2,…,0)}t2≥0，…，{T(0，0，…，tm)}tm≥0是m个单参数n阶α次积分C半群，且它们分别由线性算子A1,A2,…,Am生成，则A1,A2,…,Am在X上是闭的。令u=(a1,a2,…,am)∈Rm，则

其中S(h)=T(hu)，则{S(h)}h≥0是单参数n阶α次积分C半群。

定理2 在空间X上，线性算子A=(A1,A2,…,Am)定义为

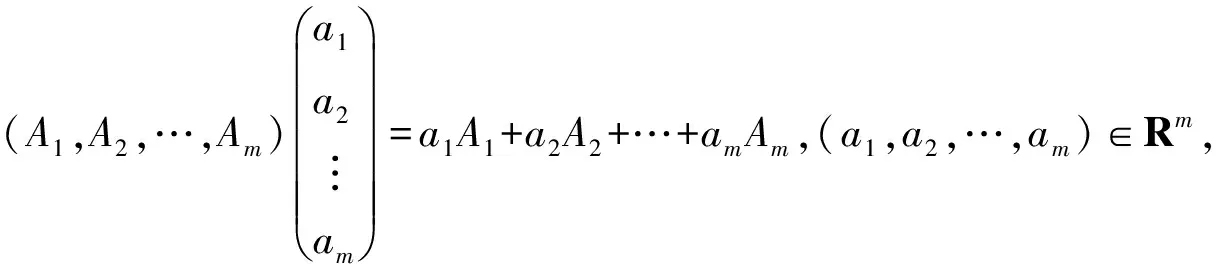
||T(t1,0,…,0)||≤M1eω1t1，

||T(0,t2,…,0)||≤M2eω2t2，…，

||T(0,0,…,tm)||≤Mmeωmtm，充要条件是：

∀(a1,a2,…,am)∈Rm；

(3)D(A1A2…Am)∩D(A1)=

D(A1A2…Am)∩D(A2)=…=

D(A1A2…Am)∩D(Am)=D≠{0}，

D(A1(λ0-A2-…-Am))⊆D(A1A2…Am)，

A1A2…Amx=AmAm-1…A1x,∀x∈D。

证明必要性：因为A=(A1,A2,…,Am)生成多参数n阶α次积分C半群{T(t1,t2,…,tm)}t1,t2,…,tm≥0，则A1,A2,…,Am分别生成单参数n阶α次积分C半群{T(t1,0,…,0)}t1≥0，{T(0,t2,…,0)}t2≥0，…，{T(0,0,…,tm)}tm≥0，并且满足

‖T(t1,0,…,0)‖≤M1eω1t1，

‖T(0,t2,…,0)‖≤M2eω2t2，…，

‖T(0,0,…,tm)‖≤Mmeωmtm，

由n阶α次积分C半群的性质[10]可得A1,A2,…,Am是闭稠定算子。

设u=(a1,a2,…,am)∈Rm，

S(h)=T(hu)=T(ha1,ha2,…,ham)，则

T(0,0,…,ham)x-T(ha1,0,…,0)x-T(0,ha2,…,0)x-…-T(0,0,…,ham)x+T(ha1,0,…,0)x+T(0,ha2,…,0)x+…+T(0,0,…,ham)x-Cx]·h-1=

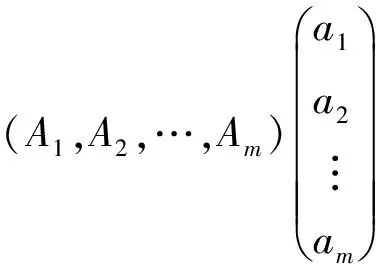
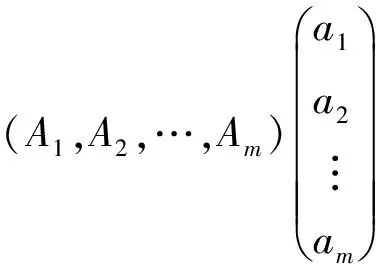
∀(a1,a2,…,am)∈Rm，

即条件(1)成立，从而可知条件(3)成立。

由文献[9]可得

Rc(λ,(A1,A2,…,Am))x=

根据{T(t1,t2,…,tm)}t1,t2,…,tm≥0的有界性，可得

‖CRc(λ,(A1,A2,…,Am))x‖=

所以条件(2)成立。

充分性：设(a1,a2,…,am)∈Rm，则

a1A1x+a2A2x+…+amAmx。

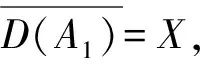
又由条件(2)可知单参数n阶α次积分C半群{T(t1,0,…,0)}t1≥0，{T(0,t2,…,0)}t2≥0，…，{T(0,0,…,tm)}tm≥0分别由线性算子A1,A2，…,Am生成，且满足‖T(t1,0,…,)‖≤M1eω1t1，

‖T(0,t2,…,0)‖≤M2eω2t2，…，

‖T(0,0,…,tm)‖≤Mmeωmtm。

由于A1，A2，…，Am满足条件(3)，所以{T(t1,0,…,0)}t1≥0，{T(0,t2,…,0)}t2≥0，…，{T(0，0，…，tm)}tm≥0可以交换，且映射t1→(t1,0,…,0),t2→(0,t2,…,0)，…，tm→(0,0,…,tm)是一一对应的，则可以把T(t1)，T(t2)，…，T(tm)分别看成T(t1,0,…,0)，T(0,t2,…,0)，…，T(0，0，…，tm)，因此

T(t1,t2,…,tm)‖=

C-1T(t1,0,…,0)T(0,t2,…,0)…T(0,0,…,tm)，

即‖T(t1,t2,…,tm)‖=

‖C-1T(t1,0,…,0)T(0,t2,…,0)…T(0,0,…,tm)‖≤

‖C-1‖‖T(t1,0,…,0)‖‖T(0,t2,…,0)‖…‖T(0,0,…,tm)‖≤

‖C-1‖M1M2…Mmeω1t1+ω2t2+…+ωmtm。

所以{T(t1,t2,…,tm)}t1,t2,…,tm≥0是满足

‖T(t1,0,…,0)‖≤M1eω1t1，

‖T(0,t2,…,0)‖≤M2eω2t2，…，

‖T(0,0,…,tm)‖≤Mmeωmtm的多参数n阶α次积分C半群，且由A=(A1,A2,…,Am)生成。