用综合法构造6m+3阶完美幻方
徐向东
(乌兰察布职业学院 经济管理系,内蒙古 乌兰察布 012000)
幻方是组合数学区组设计的一个新领域,与正交拉丁方存在天然联系[1-7]。完美幻方,又称全对称幻方,性质不平凡,约束条件诸多,获取不易。1985年,李立曾经将全对称幻方分为五类:4m阶、4m+2阶、6m-1阶、6m+1阶和6m+3阶全对称幻方,探索其构造方法[1]。对于6m±1阶全对称幻方,按连续摆数法,采用中国象棋马步和士步排序法构成,并通过几种变换得到若干构造方法[1];对于4m阶全对称幻方,李立给出十种构造方法[2]。
对于构造6m+3阶完美幻方,方法相对比较复杂。本文首先按自然数序列,构成n=6m+3阶方阵的行列编码,接着实施同步变换,再将变换后的方阵按连续摆数法,采用中国象棋马步和炮步走法[记作H(k+1,j+2)+G(k+2,j)步]并结合排序法,构造出6m+3阶完美幻方。此方法不同于王辉丰和詹森的构造方法[3]。
1 预备知识
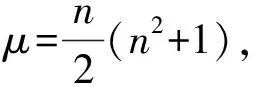
设{n}表示集合{1,2,3,…n},
(1)
(2)
(3)
(4)
其中 本文规定如下排列: U=(1,2,3…n)=(1,2,3,4,5,6,…,6m+1,6m+2,6m+3)=(u1,u2,u3,…,u6m+1,u6m+2,u6m+3), (m,n为正整数,n=6m+3), U2=(<1>n,<3>n,<5>n,…,<2n-1>n)= 引进变换: C’U:u4→c6,u5→c4,u6→c5,u7→c8,u8→c9,u9→c7,ui→ci(i=1,2,3,3m+7,3m+8,3m+9,…,6m+3),ui→c3m+16-i(10≤i≤3m+6)。 令C=(c1,c2,c3,…,c6m+1,c6m+2,c6m+3)为U的一个变换,满足 (5) 定理1 按照连续摆数法,采用中国象棋马步和炮步走法[记作H(k+1,j+2)+G(k+2,j)步]并结合排序法,可以构造出n=6m+3阶完美幻方。 其过程如下: 首先将自然数数列{n2}按顺序从上到下、从左到右排成n行n列方阵Zn, Zn=(z1,z2,…,zn),其中zi=(i,i+1,i+2,…,i+n-1)T,(T表示转置),称为自然数序列n阶方阵。其次对Zn进行行列编码的同步变换: 令Qi=(0,0,0,…,ec3i-2,ec3i-1,ec3i,…,0,0,0)n, (i={2m+1}), 其中ek为第k个分量为1、其余分量皆为0的单位向量。 (i={n}); PU∶Pu1= (i={2,3,…,n}), PjU=PPj-1U,P0U=IU,(j={n}); HjU2=H(Hj-1U2),H0U2=IU2,(j={n})。 设上述Fn=(fkj)n×n,又设Mn=(mkj)n×n,做变换: 以M9的构造过程为例,首先将自然数序列方阵Z9进行行列编码的同步变换,Z9→F9,然后从m1,1开始,按中国象棋马步[H(k+1,j+2)步]排列F9的第一列“1,2,3,5,6”,此时“6”已在方阵M9的右边上,可将方阵M9左右两边连成一圆筒,接着排列“4,9,7,8”,F9的第一列已排完;此时“8”已在M9的最下边,可将方阵M9上下两边连成一圆筒,从“8”到“10”(F9第二列的第一个数)按中国象棋炮步[G(k+2,j)步]排列(炮步称为列与列之间的过渡步);F9第二列从“10”到“17”均用马步排列,马步称为内连续步;一直排到F9的最后一个数“71”。这样就得到一个9阶完美幻方M9,如文末举例所示。用同样的方法可以构造15阶,21阶,…,6m+3阶完美幻方。 Mn=nAn+Bn+E, 其中E为所有元素全为“1”的n阶方阵。 下面证明An和Bn是满足条件(1)~(4)的完美拉丁方。 首先证明,An是满足条件(1)~(4)的完美拉丁方。 可以验证, (6) (7) (8) (9) (9)式左端各条对角线的起始元素和右端向量的起始元素并不是一一对应的,但是总和是相等的。 其次证明Bn是满足条件(1)~(4)的完美拉丁方。可以验证, (10) (11) (12) (13) (12)、(13)式左端各条对角线的起始元素和右端向量的起始元素并不是一一对应的,但是总和是相等的。 最后证明Mn=nAn+Bn+E是满足条件(1)~(4)的完美幻方。可以验证, (n+1)L+n=μ, j={n}。 类似可得Mn满足条件(2)~(4)。故Mn是6m+3阶完美幻方。 下面给出9阶自然数序列方阵Z9和其对应的同步编码变换方阵F9,完美幻方M9及正交完美拉丁方A9,B9示例。2 构造6m+3阶完美幻方


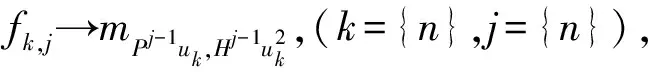
3 6m+3阶完美幻方的证明
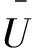







4 6m+3阶完美幻方举例

