卡尔曼滤波算法在隧道结构沉降分析降噪中的应用

王宾宾

(中铁第一勘察设计院集团有限公司 轨道交通工程信息化国家重点实验室， 西安 710043)

铁路客运、货运专线穿越高山峻岭时需要穿越隧道，城市地铁线路几乎全程运行于隧道之中，而随着我国轨道交通工程的迅速发展，隧道开挖里程日益增加。隧道结构的稳定性一直是人们关注的焦点，直接影响铁路运行安全，隧道结构的变形监测与分析能够及时发现安全隐患，有助于及时采取措施避免安全事故的发生[1-2]。

变形分析中常用的去噪方法有时间序列、灰色系统分析、BP神经网络和卡尔曼滤波等[3-7]。卡尔曼滤波是一种动态系统分析方法，它将物体的运动过程用一组状态微分方程和观测方程描述，通过不断预测与修正实现对动态运动过程的滤波和预测。卡尔曼滤波不需要存储大量的历史数据，可以跟随观测值边观测边预测，处理效率高，因此在变形分析中得到了广泛应用。卡尔曼滤波初值的选取对滤波过程影响较大，且状态向量的随机模型只能根据经验得到，不合理的初值和随机模型可能引起滤波发散。许国辉等[8]对滤波初值的选择和模型的确定进行了探讨，并通过实例证明了方法的有效性。方差补偿自适应卡尔曼滤波可以利用剩余观测值的预测残差估计动态噪声的方差并予以修正，可有效避免滤波发散。

1 经典卡尔曼滤波算法模型

卡尔曼滤波根据系统的时间特点可分为连续系统和离散系统[9]。隧道结构沉降监测是按照一定的时间间隔对监测点进行观测，确定监测点的周期变化量，其处理过程是一个典型的离散线性系统滤波问题。

1.1 离散线性系统的数学模型

离散线性系统的数学模型由一个具有随机初始状态，并带有动态噪声的线性微分方程和离散观测方程描述。离散线性系统的状态方程和观测方程为[10-12]：

(1)

式中：Xk、Xk-1为状态向量，Ωk-1为动态噪声，Lk为观测值向量，Δk为观测噪声，Φk,k-1为状态转移矩阵，Γk,k-1为动态噪声系数，Bk为观测方程系数。

1.2 离散线性系统的卡尔曼滤波方程

设Ωk，Δk是零均值白噪声，且两者之间完全不相关，X0的先验期望为(0/0)，方差为DX(0)，X0与Ωk、Δk不相关。按照广义二乘原理，增加虚拟观测值并逐次平差后可得卡尔曼滤波递推方程为：

(2)

(3)

式(2)为一步预测公式，式(3)为修正公式。

2 方差补偿自适应卡尔曼滤波算法模型

经典卡尔曼滤波由于数学模型不合理，动态噪声和观测噪声的统计性质不准确，以及递推过程中的舍入误差影响，可能会导致状态估计值偏离实际状态越来越远，出现滤波发散现象。常用的克服卡尔曼滤波发散的方法有渐消记忆法、限定记忆法、限定下界法和方差补偿自适应卡尔曼滤波算法等。方差补偿自适应卡尔曼滤波算法应用广泛，该方法是在利用观测数据进行滤波时，不断对未知的或不确切的模型参数以及噪声的统计性质进行估计和修正，减少模型误差[11]208-212，215。

2.1 动态噪声方差阵的估计

定义第l步预测的残差Vk+l为：

Vk+l=Lk+l-k+l

(4)

式中：Vk+l为第l步预测的残差，Lk+l为第k+l期观测值，k+l为第k+l期最佳预测值，k+l=Bk+lΦk+l,kk，Vk+l服从正态分布N(0,Dvv)。

由式(4)可得Vk+l的方差Dvv为[13-15]：

(5)

假定DΩ(k+i-1)在第k期之后的N期时间段上为常量对角阵，即：

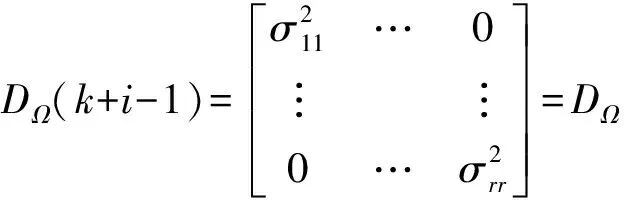
(i=1,…,l)

(6)

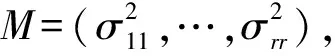
(7)

式(7)中：δk+l为零均值随机变量，l=1,…,N。

令：

(8)

将式(7)代入式(8)并顾及式(5)可得：

(9)

此时，令：

(10)

由式(9)、式(10)可得：

Wk+l=C(k,k+l)MT+δk+l

(11)

以M作为参数，由式(11)可得误差方程的一般形式：

(12)

即有：

(13)

按最小二乘原理，当N≥r时T有唯一解，组成法方程并求逆得M的估计值为：

(14)

式中：C=[C(k,k+1),…,C(k,k+N))]T，W=[Wk+1,…,Wk+N]T。

2.2 方差补偿自适应卡尔曼滤波算法流程

方差补偿自适应卡尔曼滤波在进行滤波时利用预测值和剩余观测值估计动态噪声的方差，并以动态噪声方差估计值进行新的滤波，算法流程如图1所示。

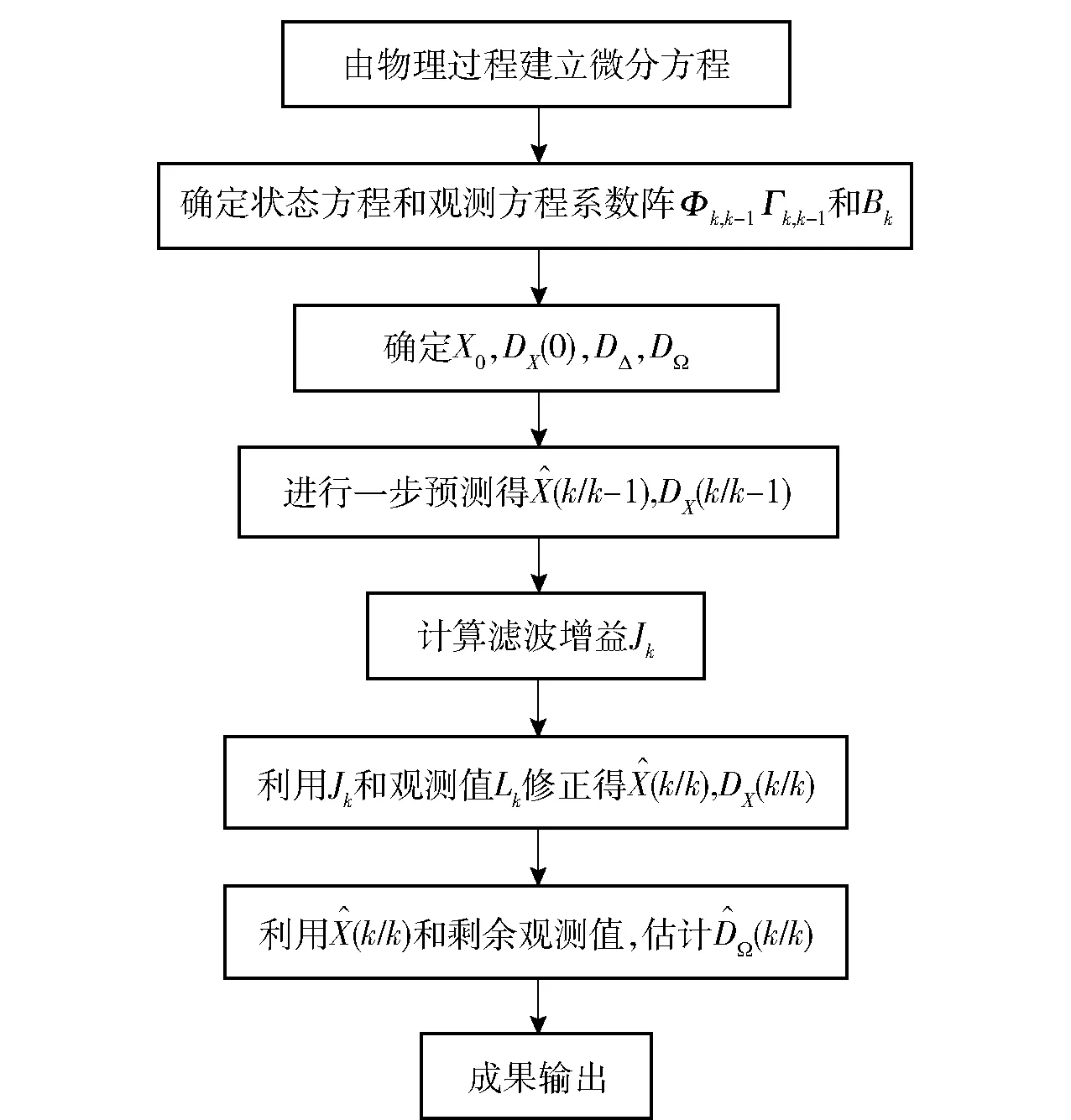
图1 方差补偿自适应卡尔曼滤波的算法流程Fig.1 Algorithm flow of variance compensation adaptive Kalman filter

3 应用实例

3.1 项目概况

广州某新建高速铁路站前工程，设计桥梁共9座，总长27.23 km；涵洞11座；隧道4座，总长4.92 km；区间路基共8段，总长1.26 km。按照相关规范要求，施工期间必须对沿线路基、涵洞、桥梁和隧道等进行动态沉降变形观测，通过对沉降观测数据进行综合分析和评估，验证和调整设计参数与措施，使路基、桥涵、隧道等线下工程达到规定的变形控制要求。本标段线下工程沉降变形观测工作以桥涵、路基、隧道等建(构)筑物的垂直位移观测为主。

3.2 布网方案

本项目隧道垂直位移监测要求采用沉降变形等级三等(国家二等水准测量)施测，根据沉降变形测量精度要求高的特点，以及标志的作用和要求不同，垂直位移监测网布设分为基准点网、工作基点网和沉降变形观测网三级。

本项目要求观测隧道的仰拱部分，隧道水准路线观测按二等水准测量精度要求形成闭合或附合水准路线，沉降观测点位布设于观测断面隧道仰拱顶面，图2为附合水准路线示意，图3为观测点位埋设示意。

图2 附合水准路线示意Fig.2 Diagram ofannexed leveling line

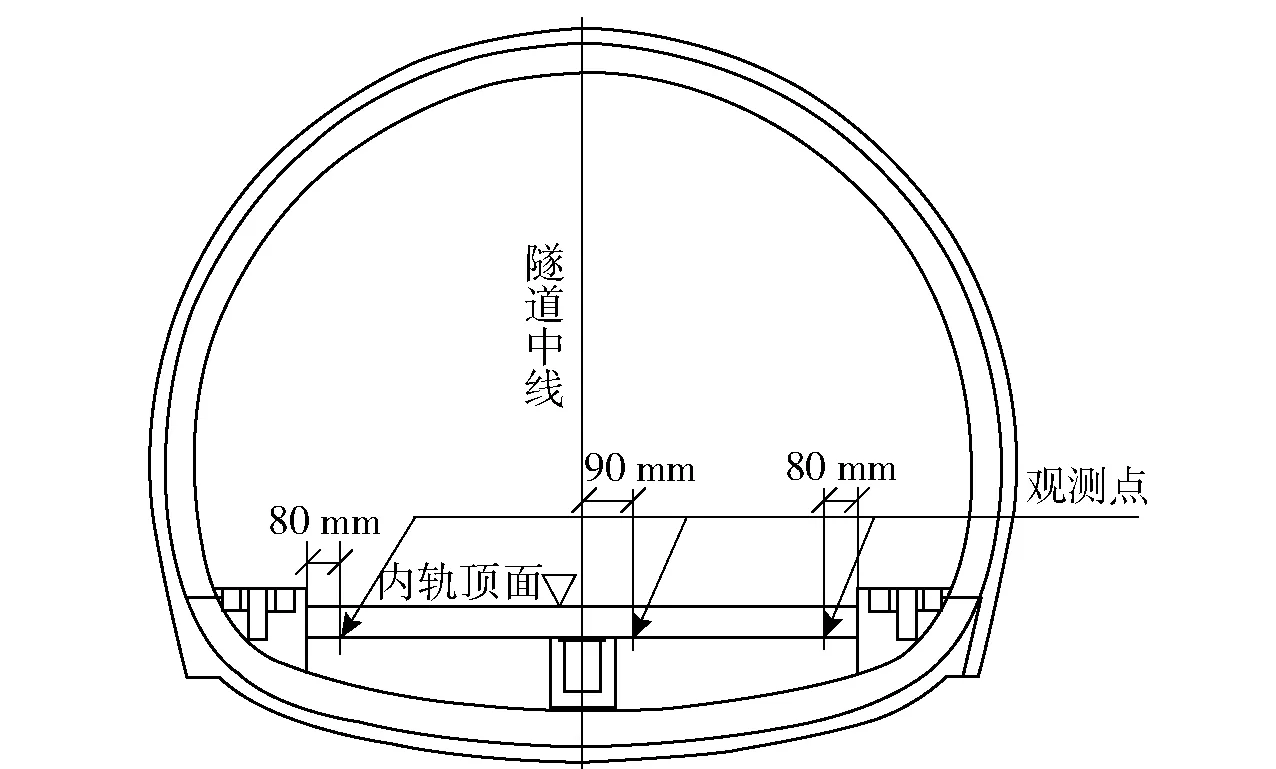
图3 观测点位埋设Fig.3 Diagram of points buried

3.3 滤波分析

以该项目中隧道闭合水准线路L93764为例，线路起闭于JM237点，共观测18个点，其中JM237和JMX- 4为工作基点不计算沉降量，中间设置16个监测点，观测方案见表1，该线路观测频率为1次/5天，共观测26期数据。

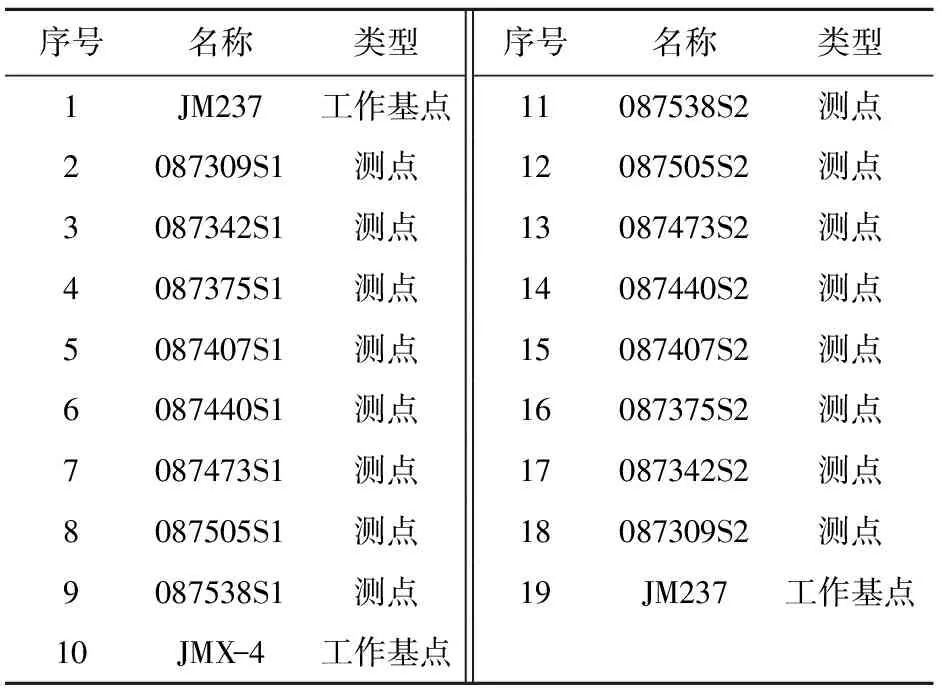
表1 L93764水准线路观测方案

以087440S2点的26期数据为例，对文中方法进行可行性和有效性的验证与分析，原始沉降数据见表2，表2中的首期数据不计算沉降量和沉降速率。

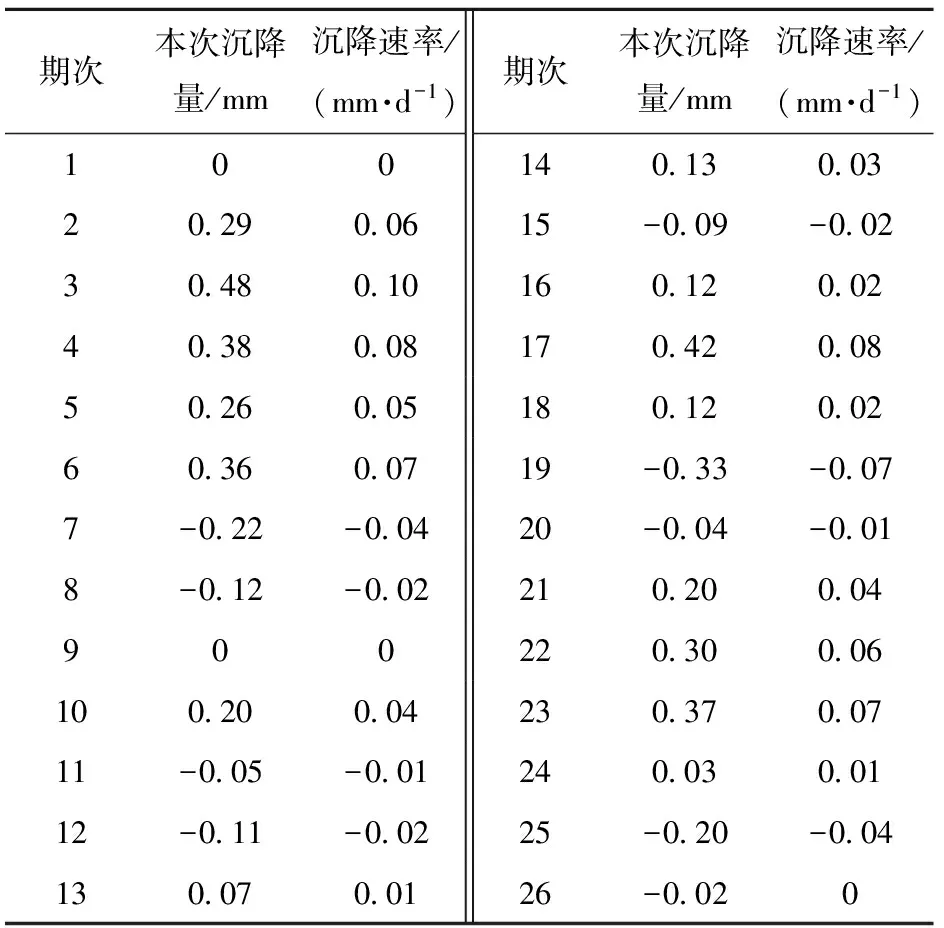
表2 087440S2原始沉降数据

选取该点前5期沉降量和沉降速率的平均值作为初值，分别利用经典卡尔曼滤波算法和方差补偿自适应卡尔曼滤波算法进行分析，经过滤波后的沉降量如图4所示，可以看出经卡尔曼滤波处理后的沉降量大大降低了测量噪声，且随着时间的推移，波动量逐渐变小并能更加合理地反映监测点的沉降趋势。

图4 卡尔曼滤波结果Fig.4 Graph of Kalman filter results

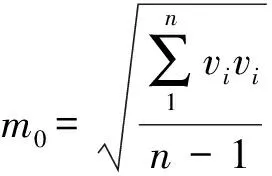
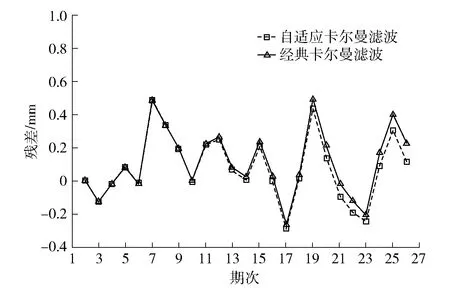
图5 卡尔曼滤波残差Fig.5 Graph of Kalman filter residual

4 结论

本文分别利用经典卡尔曼滤波算法和方差补偿自适应卡尔曼滤波算法对隧道结构进行沉降分析，通过工程项目算例得出如下结论：

1)隧道结构的沉降测量中伴随着各种测量噪声，若直接利用原始测量值对监测点进行分析，在沉降量比较小、信噪比较低的情况下，测量噪声对隧道结构的稳定性判定影响非常大，因此必须采用滤波方法降低测量噪声。

2)卡尔曼滤波算法能够有效减小沉降分析中的误差影响，使测量数据能够更加真实反映隧道结构的沉降趋势。

3)方差补偿自适应卡尔曼滤波算法在进行滤波时利用剩余的测量数据对动态噪声方差进行预计和修正，滤波后的精度高于经典卡尔曼滤波，且不易受测量误差的影响而发散。