信度加权马尔科夫链预测模型及应用
夏春芳,卫彦晶,王丰效
(喀什大学 数学与统计学院,新疆 喀什 844000)
0 引言
传统的马尔科夫模型对于易区分的离散状态显示出了很好的预测效果,对于不易区分的连续状态,无法对研究对象的状态进行确切的划分.另外,传统的马尔科夫模型通过对历史数据进行统计分析,对未来事物做出预测,忽视了不同时间的历史数据对于要推断的事物趋势的影响.针对这两个问题,多数学者建立模糊马尔科夫预测模型、加权马尔科夫预测模型,且对此进行改进.文献[1-2]根据马尔科夫链理论,提出了具备状态模糊划分的模糊马尔科夫链状的预测模型,即建立一个确定的隶属函数.文献[3-4]采用对不同时期历史数据进行加权,创建加权马尔科夫链预测模型,并用级别特征值法对预测对象进行定量分析,计算预测值.文献[5]提出一种信度马尔科夫模型,针对研究对象状态的不确定性引入D-S理论进行描述,获得了较经典马尔科夫链更加精确的结果.文献[6]在[5]的基础上对状态间转移矩阵的方法进行改进,并用D-S理论对原始数据所处状态处理后,得到相应的信度函数值,通过对后退偏差平方和进行加权形成转移矩阵,然后计算回代误差,最终得到比文献[5]更精确的预测结果.
针对以上问题,对文献[3]和文献[6]的方法进行了结合,主要包括两个方面:一是引入D-S理论对连续值状态建立状态信度函数,划分状态区间;二是以规范化的各阶自相关系数为权重,以及模糊数学中的级别特征值法对预测对象进行定量分析.最后通过实证分析对比,证明了本文方法的有效性.
1 信度加权马尔科夫链预测模型
对于无法明确状态区间的序列,建立传统马尔科夫预测模型往往达不到很好的效果.因此引入D-S理论对连续值状态建立状态信度函数,划分状态区间,再以规范化的各阶自相关系数对不同时期的历史数据进行加权,构建预测状态转移概率矩阵,这一方法可以有效提高预测精度.
1.1 变量状态的划分
建立信度概率指派函数:设Θ为所有可能性的有限集合,函数m:2Θ→[0,1],且满足:
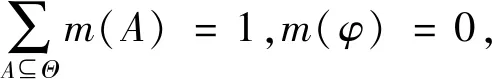
则称m为Θ上的基本信度指派函数[6].
建立连续值状态信度函数:设过程所处的状态X为连续值状态,分别用x(1)和x(n)表示状态所处最小值和最大值,则X∈(x(1),x(n)).将所有数值归为低、中、高3种基本状态,分别用L,M,H来表示,则Θ={L,M,H},其中
L=[x(1),x(1)+b),M=[x(1)+b,x(n)-b],
H=(x(n)-b,x(n)],b=(x(n)-x(1))/5,
将t时刻所有取值归为5种状态,分别为:
S1={L},S2={L,M},S3={M},
S4={M,H},S5={H}.
建立状态信度指派函数m如下:
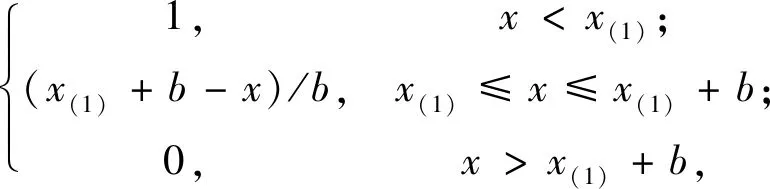
(1)
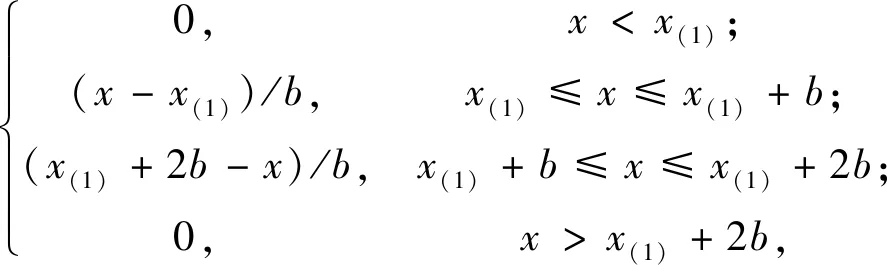
(2)
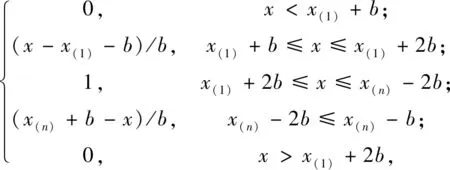
(3)
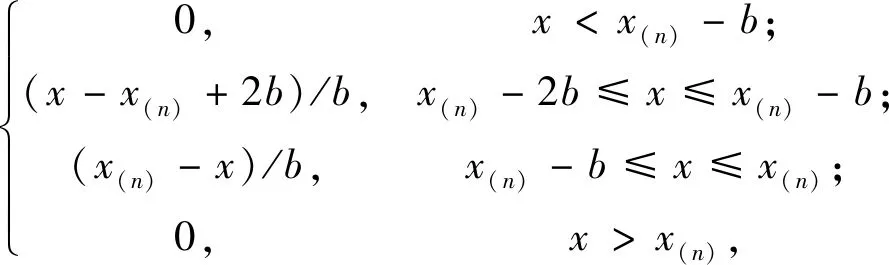
(4)
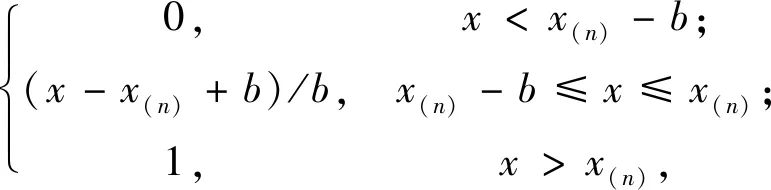
(5)
mL,H(x)t=0,mL,M,H(x)t=0,mφ(x)t=0.
对于任意的x,有
m(L)(x)t+m(L,M)(x)t+m(M)(x)t+
m(M,H)(x)t+m(H)(x)t=1.
记:
m(t)=(m(L)(x)t,m(L,M)(x)t,m(M)(x)t,
m(M,H)(x)t,m(H)(x)t)=
(mt(1),mt(2),mt(3),mt(4),mt(5)).
其中,mt(i)表示t时刻状态Xt所属状态Si的可能性的大小,因此得出每个时刻t对应的信度指派函数mt.
1.2 计算状态转移概率矩阵
1步状态转移概率矩阵P1={pij},其中
pij=sij/∑si.
(6)
其中,sij是状态Si经过1步转移到状态Sj的次数;∑si是状态Si在样本中出现的总次数.
n步状态转移概率矩阵为
(7)
1.3 计算各阶的自相关系数和权重
阶数为状态转移的步数,也称步长或滞后期,各阶自相关系数为
(8)
其中,rk为k阶的自相关系数;n为样本长度.
根据自相关系数确定各时间段值(阶数)的权重为
(9)
1.4 构建预测状态转移概率矩阵
根据各步长的状态转移概率矩阵,构建预测状态转移概率矩阵为
(10)
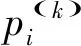
各状态概率等于预测状态转移概率矩阵中各阶状态转移概率与各阶的权重乘积的和,即
(11)
1.5 求级别特征值
计算各阶的模糊数,
(12)
其中,di表示第i阶模糊数;η表示最大的概率作用指数,一般η=2或4,η值越大,最大概率作用越明显.级别特征值如下:
(13)
1.6 求变量的预测值
变量在t+s时刻的预测值为
(14)
其中,Ti和Bi分别代表状态Si的 上限和下限;i表示状态级别.
2 实证分析
为证明本文方法的有效性,借鉴文献[5]中的数据进行预测误差对比,来说明本文方法的有效性,所用数据见表1所列.

表1 产品E15的连续20期库存需求统计
2.1 实证过程
(1)划分状态区间
建立各时刻对应的信度指派函数,划分状态区间,可得5种状态的具体范围如下:
S1={137,143},
S2={152,164},
S3={171,200},
S4={204,218},
S5={225,229}.
得到各状态分布表,见表2所列.

表2 各状态分布表
(2)计算转移概率矩阵
首先根据公式(6)计算得出1步转移概率矩阵如下:
p1=

根据1步状态转移概率矩阵p1,可得到2,3,4,5步转移概率矩阵,依次如下:
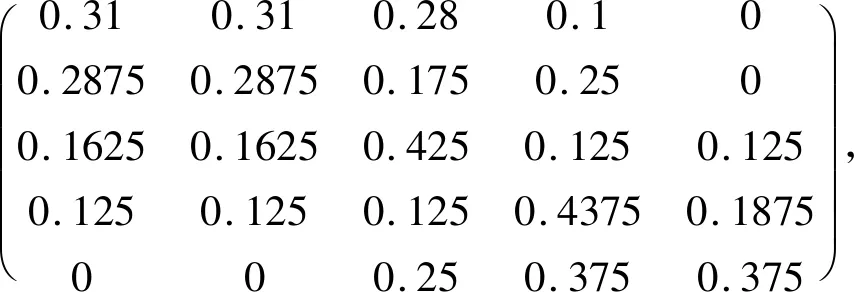
(3)计算各阶相关系数
根据公式(8)计算得出各阶相关系数如下:
r1=0.000047,r2=0.000042,r3=0.000048,
r4=0.000045,r5=0.000021.
(4)计算各阶权重
根据公式(9)计算得出各阶权重如下:
ω1=0.233186511,ω2=0.207339419,
ω3=0.236202021,ω4=0.220007107,
ω5=0.103264943.
(5)构建预测状态转移概率矩阵
以时间1,2,3,4,5所处的状态,构建相应的预测状态转移概率矩阵来预测时间6的数量.预测状态转移概率矩阵见表3所列.
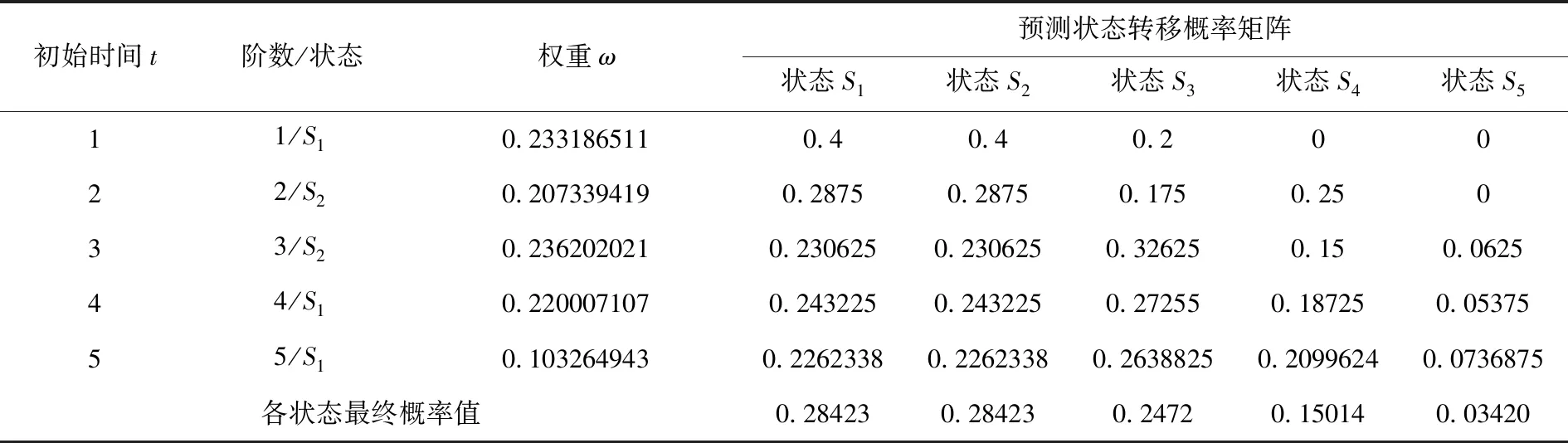
表3 预测状态转移概率矩阵
由公式(10),将权重ω与预测状态转移概率矩阵中各行的数值相乘,得出五列矩阵后,再将列元素相加,得到各状态最终概率值.由表3可见,状态S1和S2所占权重最大.真实情况下,时间t=6时状态为S3,因此预测状态选择S2.
(6)计算级别特征值
根据公式(11),取概率作用指数η=2,计算出状态模糊数为:
d1=0.32788,d2=0.32788,d3=0.24800,
d4=0.09149,d5=0.00475.
根据公式(12)计算出级别特征值为
H=2.11734.
(7)求变量的预测值及预测误差
由于级别特征值小于状态,由公式(13)求得时刻6的预测值为
t6的实际值为174,所以预测误差为
ε6=|139-174|/174≈0.2017.
2.2 结果对比
根据以上步骤,计算出其他时间的状态,最终得到预测状态对比见表4所列.

表4 预测状态对比表
按照上述计算时刻6的预测值的方法,计算其他各时间的预测值以及预测误差,并与文献[6]中的预测误差进行对比,详情见表5所列.
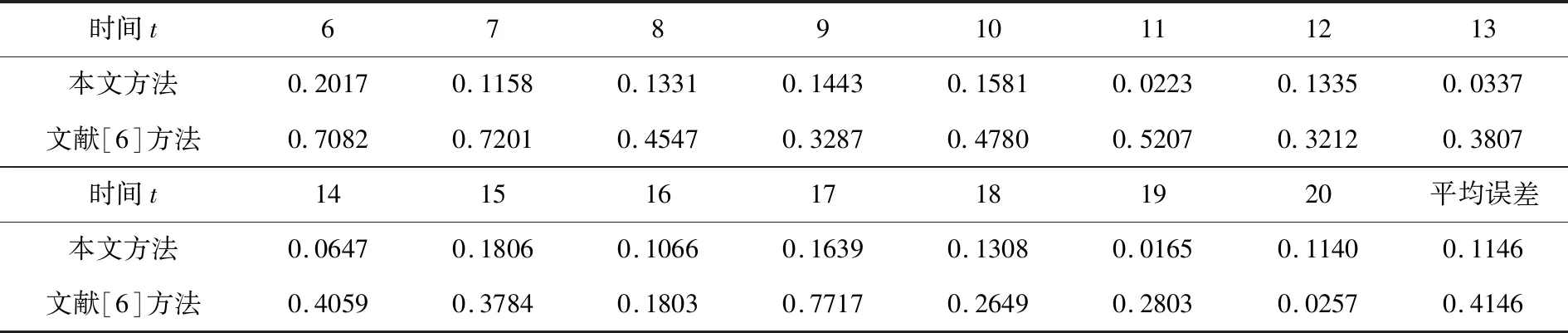
表5 预测误差对比表
由表4可知,本文所用方法的预测状态准确率为46.7%,高于文献[6]中方法得到的准确率40%.
由表5可知,本文所用方法的预测误差明显低于文献[6]中的方法得出的预测误差.
3 结语
本文针对经典马尔科夫链在预测时存在的问题,进行了两个方面的改进,首先对于无法确切划分状态的研究对象,引入D-S理论对初始对象进行处理得到与其对应的信度函数值,从而划分了5种状态区间.其次以规范化的各阶自相关系数为权重,使其能够体现不同时间历史数据对要推断事物趋势的影响,并用模糊数学中的级别特征值法对预测对象进行定量分析,计算出预测值以及预测误差,与文献[6]中的结果进行对比,结果显示本文的方法预测的准确率更高,误差更小,表明了本文方法的有效性.
——基于体育核心期刊论文(2010—2018年)的系统分析

