改进灰色波形预测方法在降水量预测中的应用

郝慧慧，朱涵钰

（华北水利水电大学管理与经济学院，郑州450046）

0 引 言

降水量和日常生活的旱涝预报、水文水情分析的研究息息相关[1]。随着人类活动加剧，大量温室气体排放，全球温度不断升高。干旱和极端降水频繁发生，给国家经济发展和人类生产、生活造成严重影响，甚至威胁到人类生命财产安全[2]。降水量的多少直接关系到农业发展以及各项政策的制定与实施，建立有效的降水量预测预警模型对我国各行各业的发展具有重大意义[3]。因此，对降水量数据序列进行分析与预测，可为区域水资源合理利用和防汛减灾工作提供数据支撑，对保证国民经济和社会发展具有重要意义[4]。

降水量预测模型可以概括为解释型和数据驱动型[5]。对于解释型模型，Priya 等[6]采用ARIMA 模型进行了印度西部季风前降雨数据的趋势分析。张帅等[7]选取了递归神经网络模型（RNN）解决了降雨量长期预测问题，并选用前馈神经网络模型（FNN）、小波神经网络模型（WNN）和整合移动平均自回归模型（ARIMA）进行对比分析。Byung 等[8]采用ARIMA 模型进行了蒙古地区降水量时空变异性评价和季节性预测。对于数据驱动型模型，宋帆等[9]基于聚类分析的模糊马尔科夫链模型，对全国16 个站点的降雨量进行预测。卢维学等[10]采用随机森林算法的偏最小二乘回归（PLS）模型，对城市的降水量进行预测。梁显丽等[11]基于加权马尔可夫预测模型对鄂尔多斯市1961−2019年的降水量数据进行预测。熊文真等[12]采用HP−ENN−MC 模型预测了某地区1990−2015年植物生育期的降雨量。上述模型对时间序列的数据要求比较苛刻，同时不能很好地描述数据序列的复杂性，限制了模型的使用与发展。

随着灰色系统模型的提出与发展，诸多学者开始转向利用灰色预测模型对降水量数据进行预测和仿真研究。任晔等[13]采用灰色神经网络组合预测模型对黑龙江省庆安县年降雨量进行了预测建模。严小华[14]采用GM(1，N)模型进行了巢湖区域主汛期降水量长期预测。吴秀明等[15]基于离散型灰色DGM(1，1)预测模型对鞍山市1959−2006年的降雨量进行涝灾预测。谢道文等[16]基于灰色系统分析理论建立了优选模型对降雨量监测点进行了选择。结果表明灰色模型对具有贫信息、不确定性、指数特征的数据序列具有很好的预测效果。而实际的降水量具有非线性、非平稳的特点，受自然和人为因素的影响，降水量随时可能产生跳跃、摆动的特征，导致模型预测效果不够理想。因此，针对数据特征波动不稳定的特点，引入分位数构建非等间隔等高线；针对数据具有上升或下降的波动特点，引入斜率等高线；本文构建了斜率非等间隔灰色波形预测模型。并对河南省降水量进行预测，验证了模型的有效性。

1 研究区概括与数据选取

河南省位于中国中东部地区，地理位置为北纬31°23'～36°22'，东经110°21'～116°39'，东连安徽、山东，南靠河北、山西，北邻湖北，土地面积为16.7 万km2，有17 个省直辖市和1 个省直管市。河南省地处亚热带和暖温带气候区，地形、地貌、土壤、气候都有明显的过渡性特征。地势西高东低，中东部为平原，西南部为丘陵，降水量多年分布不均，年际间变化较大。本文选取1990−2019年河南省降水量数据，数据来源于《河南省统计年鉴》《河南省农村年鉴》，如图1所示。

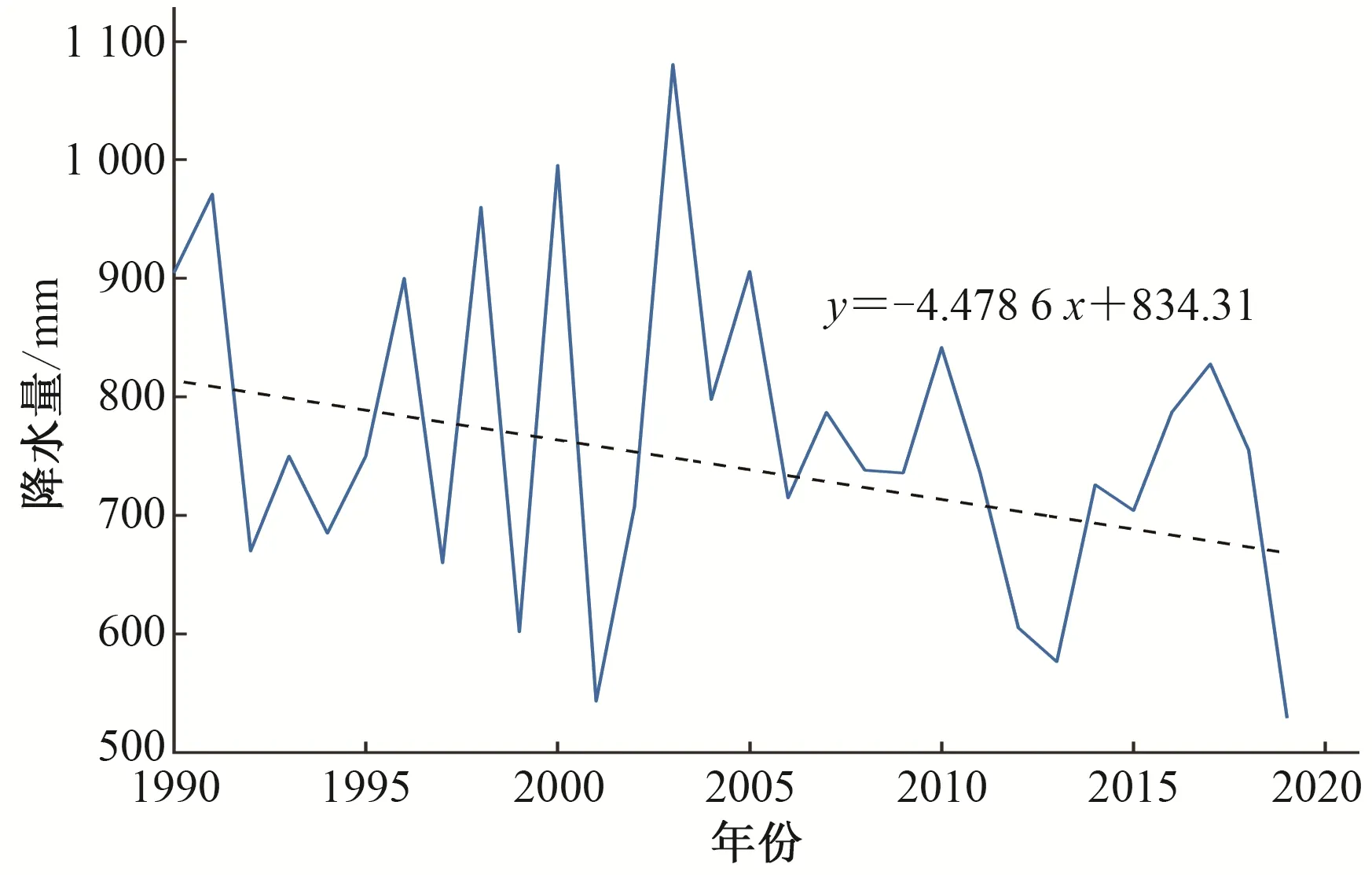
图1 河南省1990-2019年的降水量趋势图Fig.1 Precipitation trend chart of Henan Province from 1990 to 2019

2 模型构建

灰色波形预测是对数据序列的整体发展变化进行预测，该类数据具有变化不规则的特点，通过对等间隔的等高线与数据序列波动图形折线的交点横坐标进行GM(1，1)建模。该方法对摆动幅度较为固定，或者具有近似正弦波动的数据序列（图2）具有很好的预测效果。等高线的选取、确定等高时刻序列、对等高时刻序列进行GM(1，1)建模为灰色波形预测模型的3个步骤。等高线的选取和确定等高时刻序列可以看做是提取数据图形信息的过程，根据等高线和数据折线的交点提取规律信息进行GM(1，1)建模。

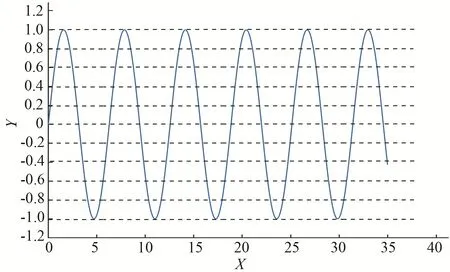
图2 具有正弦波动趋势Fig.2 It has a sinusoidal trend

2.1 选取等高线

传统的灰色波形预测模型是选取等间隔的水平等高线建立GM(1，1)模型群，该方法对于平稳周期性水平波动的数据具有较好的预测效果。对于呈现上升（图3）、下降（图4）或波动幅度不稳定（图5）的数据序列，无法根据数据波动特征准确高效的提取图形信息。因此本文引入分位数构建非等间隔斜率等高线波形预测模型。

图3 具有上升波动趋势Fig.3 It has an upward trend of fluctuation

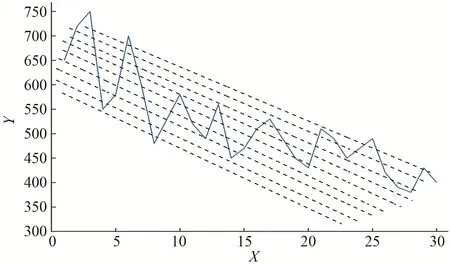
图4 具有下降波动趋势Fig.4 It has a downward trend of fluctuation

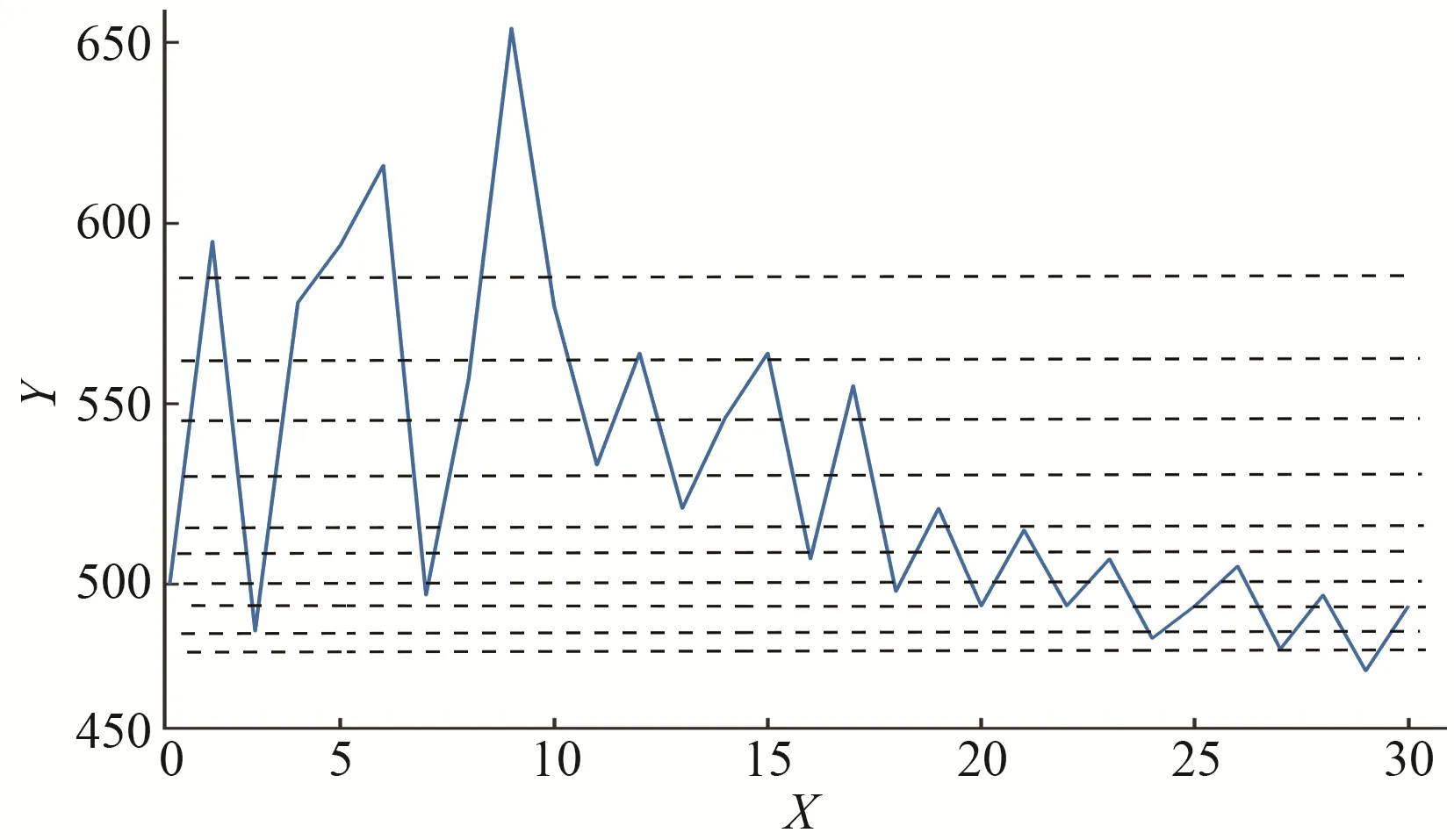
图5 具有不稳定波动趋势Fig.5 It has the tendency of unstable fluctuation

定义1：设原始序列X=(x(1),x(2),…,x(i),…,x(n))，则称xk=x(k)+(t−k)[x(k+1)−x(k)]为序列X的(k)～(k+1)段的线段，其中k∈[1,n]为整数，t∈[k,k+1]为未知参数。称{xk=x(k)+(t−k)[x(k+1)−x(k)]，|k=1,2,…,n−1}为序列X的折线，即为X={xk=x(k)+(t−k)[x(k+1)−x(k)]，|k=1,2,…,n−1}。

定义2：（斜率等高线）设原始序列为X=(x(1),x(2),…,x(i),…,x(n))，拟合线性回归方程为：

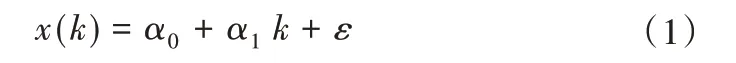
式中：ε为线性误差项；k∈[1,n]为整数。

定义3：（非等间隔等高线） 令原始序列为X=(x(1),x(2),…,x(i),…,x(n))，设原始序列的最大最小值分别为xα(i)和xα(j)。则有1°原始序列最低等高线和最高等高线为ξ0=α0+α1k和ξs=αs+α1k，其中α0=xα(i)−α1i，αs=xα(j)−α1j。2°令(ξ1,ξ2,…,ξs−1)为数据序列的s等分位，则定义ξi=α1k+α0++ξ'i,i=1,2,…,s−1。其中ξ'i=则称 (ξ0,ξ1,ξ2,…,ξs−1,ξs)所确定的斜率非等间隔等高线为原始数据的s+1条等高线。

2.2 确定等高时刻序列

根据2.1 节确定的非等间隔等高线，按照等高线序列出现的时间先后顺序确定等高时刻序列。

定义4：（等高点） 设方程组（2） 的解为(tl,x(tl)),l=1,2,…，则(tl,x(tl)),l=1,2,…为ξi−等高点，是折线X与ξi−等高线的交点。

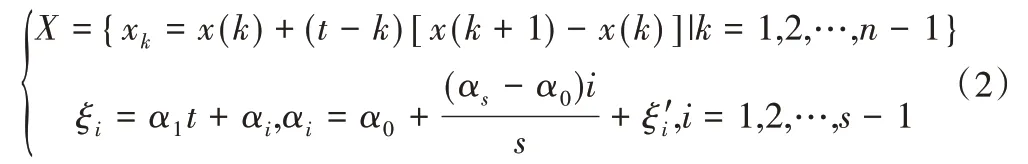
命题1：若X的第(k)～(k+1)段上有ξi−等高点，则其坐标为 ：

证明：第(k)～(k+1) 段折线方程为xk=x(k)+(t−k)[x(k+1)−x(k)]，联立令ξi(k)=α1k+αi，ξi(k+1)=α1(k+1)+αi，则有αi=ξi(k)−α1k，α1=ξi(k+1)−ξi(k)，带入联立方程可得X的第(k)～(k+1) 段上与ξi−等高线交点的横坐标为k+

定义5：（等高时刻序列）设Xξi=(P1,P2,…,Pmi)为ξi−等高点序列，其中Pj位于第(kj)～(kj+1)段折线上，其坐标为：记qj=kj+则称Q(i0)=(qi(1),qi(2),…,qi(mi)),i=0,1,2,…,s为ξi−等高时刻序列。

2.3 GM(1，1)建模与预测

经典GM(1，1)建模至少需要4个数据才能完成。因此，本文构建的非等间隔斜率等高线波形预测模型对含有4 个及4 个以上元素等高序列的横坐标建模。

定义6：设Q(i0)=(qi(1),qi(2),…,qi(mi)),i=0,1,2,…,s为ξi−等高时刻序列，为ξi−等高时刻序列GM(1，1)预测值，删除无效预测时刻，并将剩余预测值从小到大进行排序，得到(1) <(2) <…<(ns)，其中若X=ξq(k)为q(k)所对应的斜率等高线，则X(0)的预测波形为其中

3 应用分析

3.1 预测过程

依据上述分析步骤，进行等高线选取。当s=9 时，10 条等高线斜率为−4.48，常数项分别为(α0,α1,…,α9)=(663.5,720.79,777.08,833.87,890.66,946.96,1 003.75,1 060.54,1 116.83,1 173.62)。由此确定10条等高时刻序列如下：

由GM(1，1)建模性质可知，GM(1，1)建模至少需要4个数据，故本文对组等高时刻序列进行GM(1，1)建模，得到各等高时刻序列的时间响应式为：

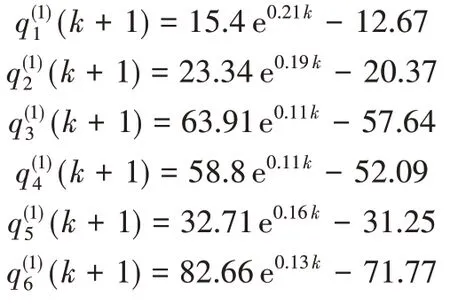
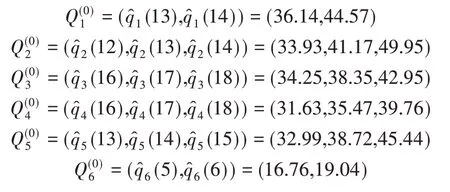
3.2 结果比较

根据等高时刻预测序列和GM(1，1)建模，得到非等间隔斜率等高线波形预测结果，如图6所示。为了验证本文模型的有效性，选用传统的灰色波形预测模型和经典的GM(1，1)预测模型进行对比分析，结果如图7和图8所示。由图7可知，传统的灰色波形预测波动性较大，主要原因是传统灰色波形预测选取水平等间隔的等高线，在提取数据时，没有考虑数据的下降趋势和分布特征，从而导致拟合数据波动性较大，拟合结果误差较高。由图8可知，经典GM(1，1)预测拟合值虽然出现明显的下降趋势，但忽略了数据的波动性特征，拟合误差较大。

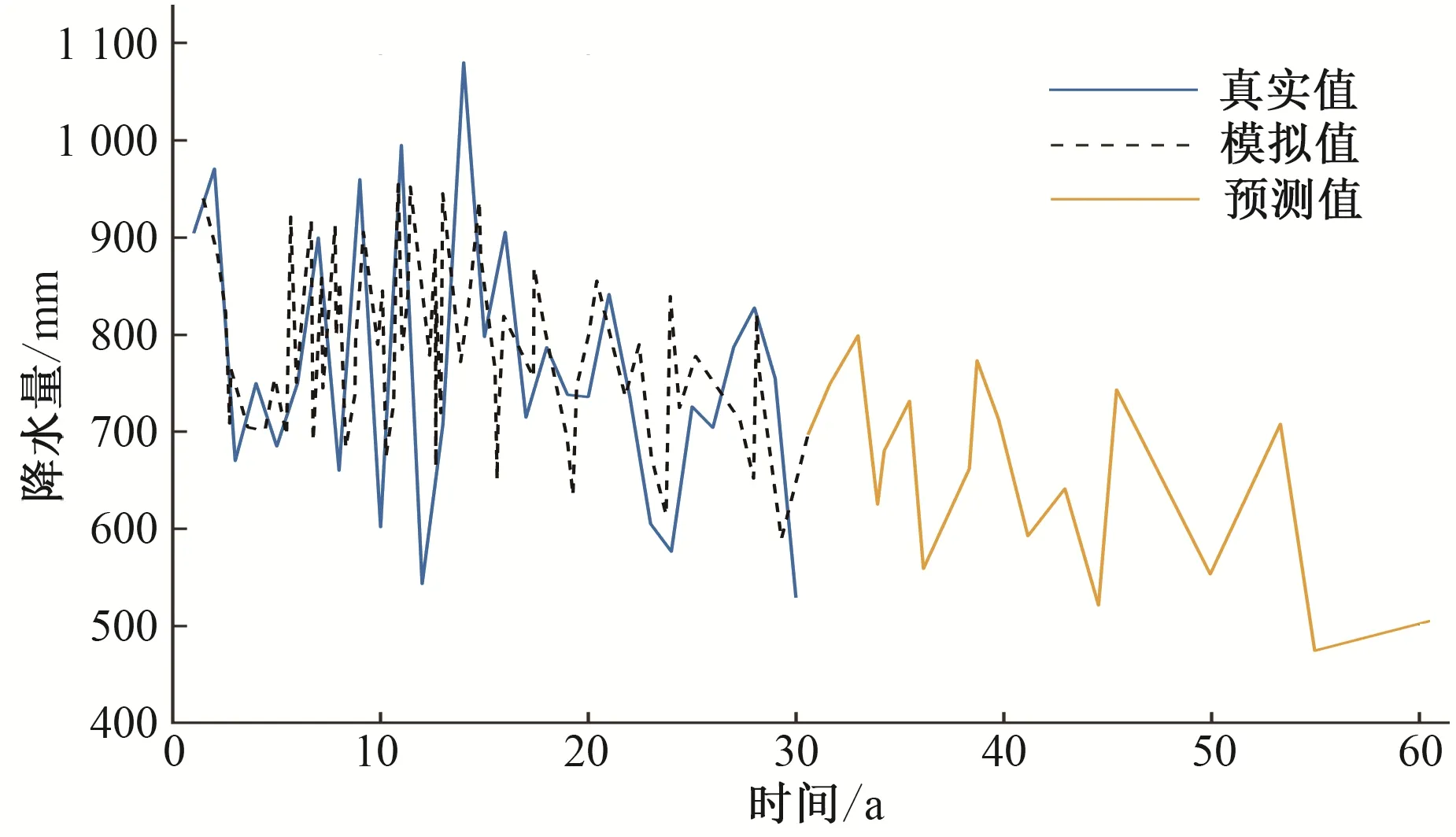
图6 改进灰色波形预测Fig.6 Improved grey waveform prediction

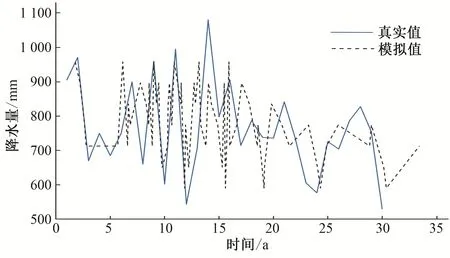
图7 传统灰色波形预测Fig.7 Traditional grey waveform prediction

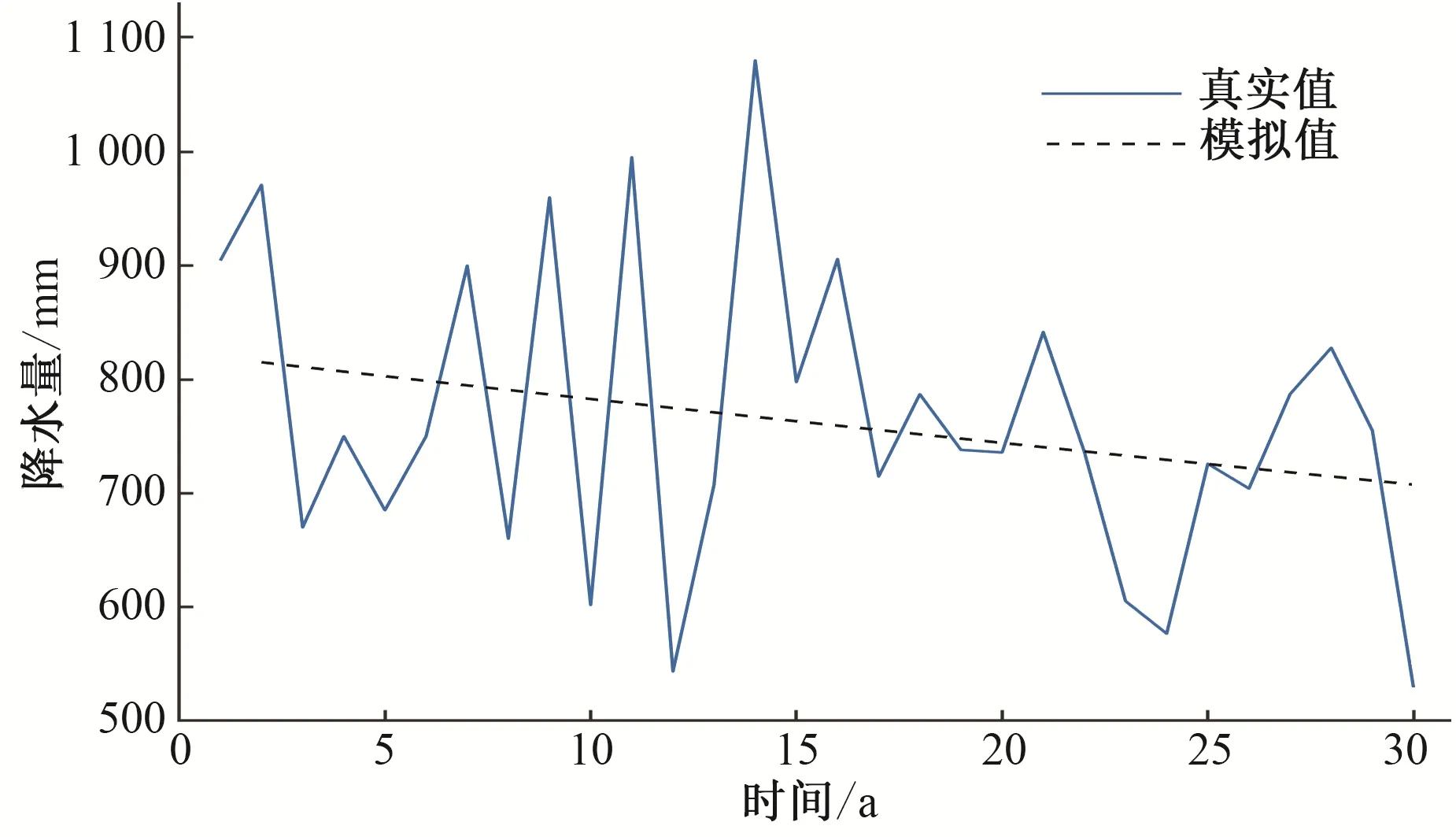
图8 经典GM(1，1)预测Fig.8 Classical GM(1，1)prediction

在预测精度方面，选用均方根误差和平均相对误差对模型精度进行检验，结果如表1所示。由表1可知，改进的灰色波形预测模型在均方根误差和平均相对误差方面均优于传统的灰色波形预测模型和经典的GM(1，1)预测模型。

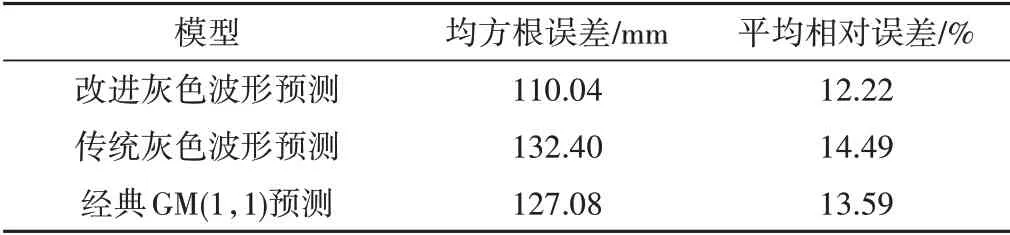
表1 预测精度对比Tab.1 Comparison of prediction accuracy

4 结 论

针对降水量年际间非平稳、非线性的特点，本文在已有波形预测模型的基础上，引入斜率非等间隔波形预测模型，选取1990−2019年河南省降水量数据进行验证。结果表明，斜率非等间隔灰色波形预测模型在预测降水量时的精度明显提高。通过对比分析可知，改进的灰色波形预测方法对于具有非平稳、非线性特征的数据序列具有较好的预测效果。目前，采用灰色波形预测模型对降水量预测的应用较少，值得研究和改进的部分还有很多，不仅体现在对模型的改进，结合其他模型对灰色波形预测模型进行优化也是未来工作的一部分。