改进遗传算法求解带不相关并行机的HFSP

王静云，王 雷，李佳路

（安徽工程大学机械工程学院，安徽，芜湖 241000）

0 引言

车间调度是典型的NP-hard 问题，混合流水车间调度问题（Hybrid flow shop scheduling problem,HFSP）是车间调度中常见的调度类型，是传统的流水线生产与并行机调度的综合。目前，混合流水车间调度广泛存在于化工、冶金、纺织、机械、装配、运输等行业中[1]。

近年来，越来越多的智能优化算法应用于HFSP。张源等在传统的差分算法上结合了反向学习策略生成初始种群，添加自适应差分因子，并在个体选择时引入Metropolis 准则[2]；Zhou 等人运用带分布估计的混合差分进化算法，求解了一种可重入混合流水车间调度问题[3]；Mageed 和Ibrahim 研究了无等待的两阶段问题，采用PSO 算法优化了总延迟时间[4]；Meng 等人针对不相关并行机的节能混合流水车间调度问题，提出了改进的遗传算法，通过对比模拟退火算法和迁徙鸟类优化算法，证明了其改进的遗传算法的有效性[5]；罗函明等针对布谷鸟算法常规解码方法难以获得最优解的缺点，提出一种改进的解码方法，通过对比原始规则解码、随机规则解码、改进规则解码所得结果，验证其有效性[6]；Mousavi 等人提出了一种基于遗传算法的近似求解方法，求解了最大完成时间和总拖延时间最小化的双目标问题[7]；杜利珍等提出了基于权重的编码方式的果蝇优化算法，来求解混合流水车间调度问题，并通过与经典算法进行对比验证了其算法的有效性[8]；宋存利采用正序解码和逆序解码，提出贪婪交叉算子变异算子，增加了种群的多样性，提高了遗传算法在求解HFSP 时的局部搜索能力[9]；轩华等人研究了可重入多阶段混合流水车间调度问题，以最小化最大完工时间为目标建立数学模型。在GA 的基础上，结合NEH 启发式算法产生工件初始加工顺序，使得遗传参数随进化代数和个体适应函数值两个方面进行自适应调节[10]。

已有的研究表明，GA 算法在求解HFSP 时全局搜索能力较好，但易陷入局部极值。针对此问题，本研究针对最小化最大完工时间为目标的不相关并行机混合流水车间调度问题进行研究。首先建立了不相关并行机混合流水车间调度问题的数学模型，然后提出了改进的遗传算法进行求解。为弥补遗传算法的迭代后期容易陷入局部搜索的缺陷，在传统遗传算法的基础上利用改进的自适应交叉和变异概率因子及模拟退火局部搜索策略，增强遗传算法在迭代后期跳出局部最优的能力。通过两个案例来验证改进遗传算法的有效性。

1 不相关并行机HFSP 问题描述

不相关并行机HFSP 可以描述为：n个工件经过m道工序的加工，所有的工件有着相同的加工路径，存在一道或多道工序有并行机，如图1 所示。HFSP 需要解决的问题就是确定每个工件在哪一台机器上加工，使得某一个或多个指标最优。

图1 混合流水车间结构Fig.1 Hybrid flow shop structure

另外，还有如下假设：

1）每一台机器只能加工一件工件，每个工件每道工序只在一台机器上加工；

2）工件一旦加工，就不能中断，直到完工；

3）不考虑工件之间的运输时间和准备时间；

4）所有工件的到达时间都为0；

5）相邻两道工序有无限的缓冲储存区。

不相关并行机HFSP有n个工件经过m道工序；工件编号为i（i=1,2,…,n）；工序的编号为j（j=1,2,…,m）；Mj为工序j 的并行机数量；Ci为工件i 的完工时间；Pijk为工件i在工序j的第k台机器上加工时间；Sijk为工件i在工序j的第k台机器上加工的开始时间；Eijk为工件i 在工序j的第k台机器上加工的完工时间；Xil为0-1 的变量，表示工件i 被安排在第l 个位置进行加工；Yijk为0-1 的变量，表示工件i在工序j的第k台机器上进行加工。

本研究优化的目标是最小完工时间，即n个工件完工时间的最小值，根据以上的问题描述，目标函数为最小化完工时间：

式（1）表示目标函数最大完工时间；式（2）表示工件在完成前一道工序才能开始下一道工序的加工；式（3）表示在同一道工序工件的加工完工时间的计算公式；式（4）、（5）表示至少有一道工序有并行机；式（6）、（7）表示工件的排序位置约束；式（8）表示工件在每一道工序只能在该工序的一台机器上进行加工。

2 改进遗传算法求解

遗传算法求解做和优化问题能获得较好的优化结果，但遗传算法在迭代后期容易陷入局部最优，本研究应用改进的遗传算法对HFSP 进行研究。改进后的遗传算法的流程图如图2 所示。

图2 改进的遗传算法流程图Fig.2 Improved genetic algorithm flowchart

2.1 编码方式

假设要加工n个工件，每一个工件要经过m道工序， 每一道工序的并行机数量为Mj（Mj>1,j=1,2,…,m）。构造一个n×m的编码矩阵：

矩阵元素aij是在区间（1，Mj+1）上随机产生的一个实数，其中实数部分表示工件i在工序j的第[aij]台的机器上进行加工，[]表示向下取整；小数部分表示工件i在工序j的第[aij]台的机器的加工顺序，数值较大优先加工。

2.2 初始种群和适应度函数

初始种群的规模为popsize，本文采用产生随机数的方式来产生初始解。本研究的混合流水车间调度问题以最大完工时间Cmax为研究问题的目标，故选择完工时间的倒数为适应度函数，即f（i）=1/Cmax。

2.3 遗传操作

2.3.1 选择

通过采用二元锦标赛选择法，从初始种群中随机选出两个个体，计算两个个体的适应度值，将适应度最优的个体放入下一代种群集合中。重复该操作，直到新的种群规模达到了原先的种群规模。

2.3.2 自适应交叉

交叉算子对种群进行迭代寻优，pc的大小决定了种群寻优的速度快慢，其值过大，会破坏原先较优解，其值过小，会导致算法的搜索速度缓慢，种群多样性较差。在种群进化的前期，应该尽可能扩大搜索的范围，增加种群的多样性，pc的取值应较大；在种群进化的后期，为了使得较优解保留下来，pc的取值应较小[11]。基于以上的分析，本文设置如下的交叉概率公式：

变异操作使得种群保持多样性，避免陷入局部最优，但pm的值过大，遗传算法便近似于随机搜索，种群寻优性差[11]。基于以上的分析，设置如下的变异概率公式：

其中pmi为个体i的变异概率，pmmax为最大交叉概率，pmmin为最小交叉概率。本文选用多点变异，随机产生多个变异位置，当满足变异条件时，将变异位置的基因用区间（1，Mj+1）的随机数代替。

2.4 精英保留策略

为防止每一代遗传操作导致上一代最优解的流失或破坏，在进行选择操作时，采取精英保留策略，将上一代经过遗传操作的种群个体进行适应度值排序，取出适应度值高的个体，用保留下来的适应度值高个体代替经过遗传操作后的适应度低的个体，使得精英个体得以保留延续。

2.5 模拟退火局部搜索

模拟退火算法的Metropolis 准则具有以一定的概率接受差解，能很好地弥补遗传算法在迭代后期容易陷入局部最优的缺点。引入以下的概率公式接受新解[12]：

Step1：设置初始参数，初始温度T，终止温度T-stop，温度下降系数α,迭代次数it，迭代次数上限为I。

Step2：在除去精英保留策略的解集中依次取解x0, 在x0的邻域内随机搜索一个新解x’，如果f（x’）＞f（x0），则接受新解，用x’代替x0，转至step5；否则下一步。

Step3：生成一个0-1 的随机数rand，按照模拟退火接收差解概率公式得到p，如果p＞rand，则接受差解，否则不接受差解。it++。

Step4：若it 小于I，转至step2，否则下一步。

Step5：更新温度，若温度达到终止温度，终止。否则转至step2。

3 仿真实验及结果分析

3.1 仿真案例1

将结合遗传自适应调节和模拟退火局部搜索的GA 记为LZGA，添加遗传自适应调节的GA 记为AGA，为测试本文算法的性能，将LZGA 与AGA和传统GA 进行对比。我们应用MATLAB 2016a 对HFSP 进行案例分析，6 个工件，经过4 道工序，三道工序机器数量分别为3 台、3 台、3 台，工件在各台机器上的加工时间如表1 所示。种群大小均设置为50，迭代次数均设置为200。应用软件进行10次仿真实验，对比所得的实验数据，结果如表2 所示，迭代图如图3 所示。

图3 收敛曲线对比图Fig.3 Convergence graph for comparison

表1 案例1 工件加工时间表Table 1 Workpiece processing information for Case 1

表2 案例1 结果对比Table2 Comparison of results for Case 1

图4 LZGA 求解案例1 调度甘特图Fig.4 Scheduling Gantt chart on case 1 by using LZGA

由表2 和图3 可以看出，GA 算法未能找到最优解，陷入局部极值未能跳出局部最优；AGA 算法3 次找到了最优解，但其在前期易陷入局部极值，在迭代中后期才跳出；而LZGA 算法10 次均找到了最优解且在迭代前期就能很快地跳出局部极值。因此在10 次的仿真实验中，LZGA 的寻优性最好。

3.2 仿真案例2

以文献[13]中的发动机加工车间为例，6 个工件经过3 道工序的加工，三道工序机器数量分别为2台、3 台、3 台，工件在各台机器上的加工时间如表3 所示。以本研究的改进遗传算法求解此案例，设置种群大小为50，最大迭代次数为200，初始温度为1000，终止温度为10，降温系数为0.97，最小交叉概率为0.7，最大变异概率为0.05。

表3 案例2 产品工序加工时间表Table 3 Workpiece processing information for Case 2

通过10 次实验仿真，对比文献算法和本研究算法所得到的结果数据，如表4 所示。由表4 可以看出，我们算法的方差为0.11，稳定性良好，10 次的结果均优于文献结果，进一步表明本文算法的有效性和鲁棒性。本研究算法求得此实例的最优解调度甘特图如图5 所示。

表4 案例2 结果对比Table 4 Comparison of results for Case 2

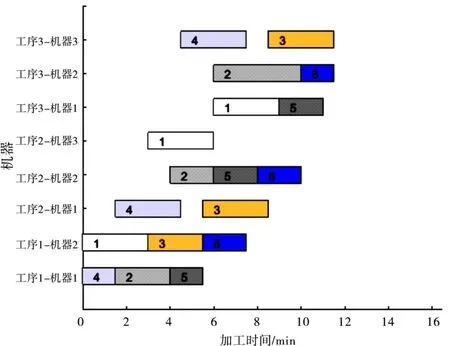
图5 LZGA 求解案例2 调度甘特图Fig.5 Scheduling Gantt chart on case 2 by using LZGA

4 结论

我们研究了不相关并行机混合流水车间调度问题，目标是最小化最大完工时间。针对遗传算法在迭代后期易陷入局部最优的缺陷，在遗传算法的交叉和变异操作中增加了自适应调节，在遗传操作后添加局部搜索策略，并用模拟退火的Metropolis准则接受差解。对比案例仿真结果表明：改进后的遗传算法更容易找到最优解，且不容易陷入局部最优，具有良好的鲁棒性和稳定性。