多点冲击荷载作用下单层球面网壳试验研究
吴长, 杨佑佩, 苟宝龙, 张瑞芹
(1.兰州理工大学 土木工程学院, 甘肃 兰州 730050; 2.甘肃省土木工程防灾减灾重点实验室, 甘肃 兰州 730050)
网壳结构在冲击荷载作用下会发生动力失稳甚至倒塌,一直以来是空间结构动力学研究领域中具有挑战性的课题。冲击荷载本身具有复杂性,其作为一种短暂而强烈的三角形脉冲荷载作用在结构上,在极短的时间内引起结构的动力响应甚至倒塌。再者,由于网壳结构本身具有复杂性和多样性,即使是冲击试验的缩尺模型也很难精确加工,且试验成本较高。因此,关于网壳结构在冲击荷载作用下的动力响应及失效模式的研究方法大多数仍然采用理论推导与数值模拟,而试验研究较少。
李海旺等[1-2]展开了K8型单层球面网壳的单点冲击试验研究,对网壳在单点冲击荷载作用下的动力稳定性进行了研究,并总结了杆件的动力响应特点。沈世钊、范峰、支旭东、王多智等[3-8]对单层球面网壳做了大量较为系统的研究,分析总结了网壳结构的冲击失效模式,提出冲击荷载下网壳结构的动力响应分析方法,并对2个相同的K6型单层球面网壳进行了单点冲击试验研究,试验结果证明了网壳结构在冲击荷载作用下的2类典型失效模式的存在以及有限元分析结果的可靠性。此后,王秀丽、吴长、马肖彤等[9-11]对带下部支撑的单层球面网壳进行了冲击试验,分析总结了结构的动力响应规律,同时也通过试验验证了4类典型失效模式的客观存在性。
文献[12-13]对网壳结构的动力稳定性和低速冲击荷载下的动力特性进行了研究。Mohammad等[14]在分析波纹构件冲击性能的基础上,研究了超高强度钢管在冲击荷载作用下对HC构件性能的贡献。
目前对于网壳结构承载力和稳定性的研究较为成熟[15-18],网壳结构在冲击荷载作用下动力响应的有限元分析与试验研究上取得了较为丰硕的成果,但是无论是有限元分析还是试验研究,对于考虑节点刚度和冲击点数量等因素对网壳结构整体动力响应及失效模式的影响的研究很少,本文基于前人研究,对采用焊接空心球节点的K6型球面网壳进行多点冲击试验研究,以此来研究冲击点数量和冲击位置对单层球面网壳动力响应的影响。
1 试验概况
1.1 模型设计
试验模型为跨度1 500 mm、矢高375 mm、频数5环的K6型单层球面网壳,网壳通过小立柱焊接在底部环梁上,环梁为方钢管,下部焊接2块带有螺栓孔的钢板,整体试验模型通过6个M24普通螺栓连接在试验平台的钢板上,钢板尺寸为1.9 m×1.9 m×0.02 m。试验模型构件尺寸如表1所示,加工完成后的试验模型如图1所示。

表1 杆件及节点参数表Table 1 Parameters of rods and nodes mm

图1 试验模型Fig.1 Text model
1.2 多点冲击试验内容与方案
网壳多点冲击试验在冲击试验台上进行,升降平台最高可升至8 m,平台两侧分别架设2个12号工字钢梁,每个钢梁配有电动葫芦和电磁吸附装置,可通过电磁吸附装置控制冲击物的自由下落,试验平台如图2所示。各试验工况方案如表2所示,本文主要研究冲击点数量及冲击位置对结构的影响,因而每个冲击点的冲击能量应保持一致,钢球选用此参数的原因是所有的试验设计工况均为弹性冲击试验,不能对结构造成破坏,具体冲击位置如图3~图6所示。
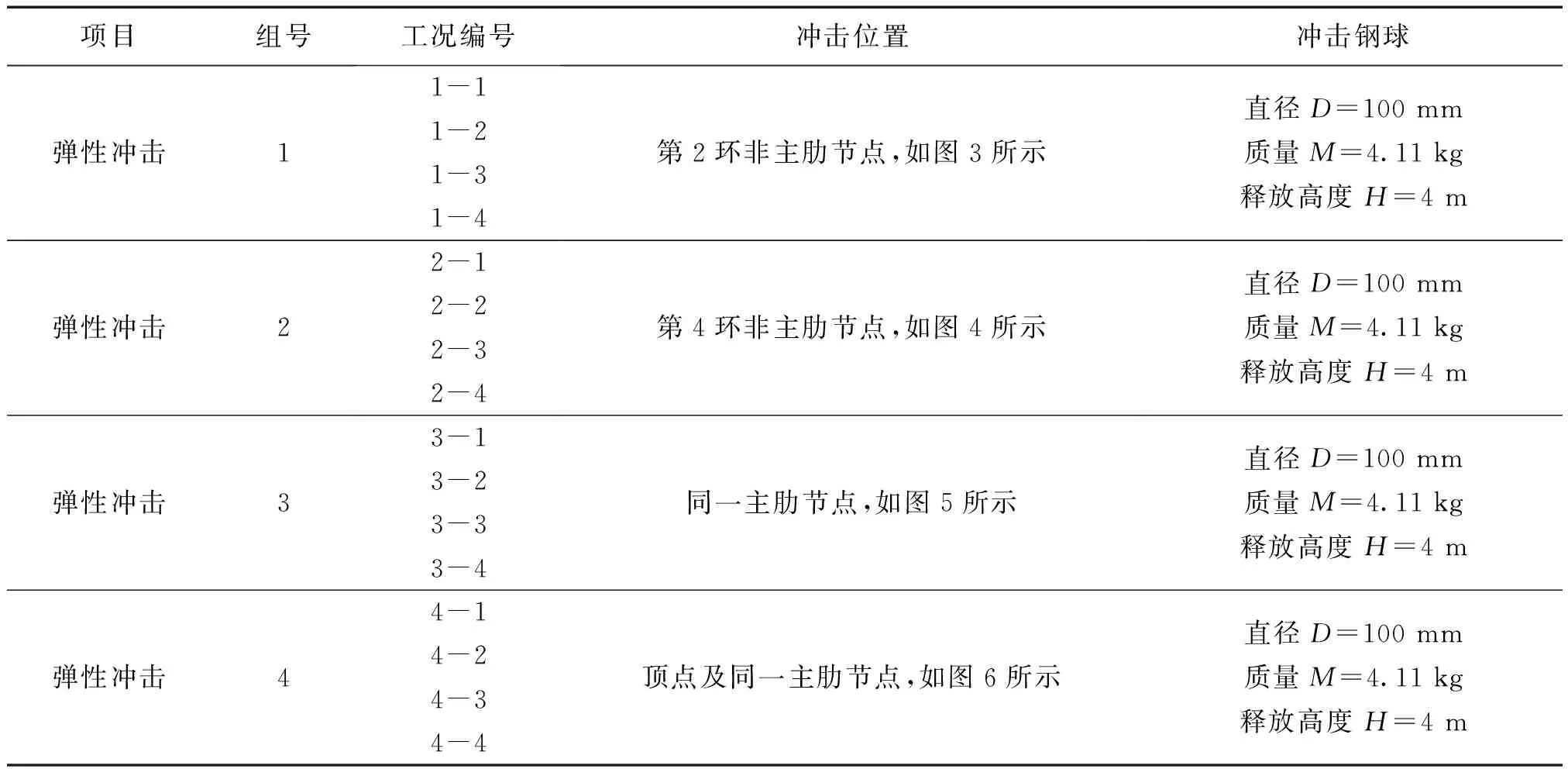
表2 动力响应试验方案Table 2 Test scheme of dynamic response

图2 冲击加载装置Fig.2 Impact loading equipment

图3 第1组工况冲击点布置Fig.3 Impact point arrangement of the first group

图4 第2组工况冲击点布置Fig.4 Impact point arrangement of the second group

图5 第3组工况冲击点布置Fig.5 Impact point arrangement of the third group

图6 第4组工况冲击点布置Fig.6 Impact point arrangement of the fourth group
1.3 测点布置与数据采集
本次试验采集的数据有关键杆件的动应变及关键节点的动位移和加速度,杆件上共布置10个应变片,编号为S1~S10;位移传感器共布置2个,编号分别为D1和D2;加速度传感器共布置3个,编号依次为A1、A2、A3,具体布置方案如图7所示,各测试元件固定安装完成后,如图8所示。

图7 测点布置方案Fig.7 Arrangement of measure point

图8 安装完成后的模型Fig.8 Model after installation
1.4 精细化有限元分析模型
在ANSYS/LS-DYNA中建立试验模型的精细化有限元模型,焊接球与杆件均采用SHELL163单元,施加冲击荷载的钢球采用SOLID164单元。金属材料承受短时超强载荷时,应变率对其材料性能有较大的影响,因此,钢材的材料模型采用分段线性塑性模型,该材料模型可考虑应变率的影响,冲击物材料模型采用刚性材料模型。精细化有限元分析模型如图9所示。
图9 数值模型Fig.9 Numerical mode
2 冲击试验结果分析
2.1 应变分析
为了研究单层球面网壳结构在不同冲击物数量及不同冲击位置下的动力响应,试验记录了每个测点的应变随时间变化的曲线,现对第1组弹性冲击试验的应变试验数据进行分析,各测点应变片的拉应变及压应变的峰值变化如图10所示。由工况1-1至工况1-3的应变峰值变化分析可知,随着冲击点数量的增多,各测点所在位置的应变值增大,由工况1-3至工况1-4的应变峰值曲线分析可知,各测点所在位置的应变值减小。


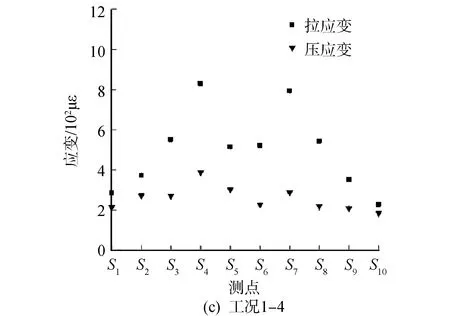
图10 工况拉压应变峰值Fig.10 The peak strain of condition
随着工况1-1到工况1-3冲击点数量增多,作用到网壳结构的总能量也逐渐增大,导致测点应变逐渐增大。由于工况1-1、1-2、1-4只有测点S4附近有一个冲击点,可以看出测点S4的拉应变明显大于其他测点。工况1-3在测点S4、S7附近均有冲击点,可以看出测点S4及测点S7处的拉应变明显大于其他测点。其中测点S4处的拉应变相较于前一个工况分别增长了9.58%、41.68%和-21.21%。工况1-3与工况1-4同为3点冲击,但工况1-3的冲击位置处于网壳结构的同一侧,冲击点较为密集,而工况1-4的冲击位置分布均匀,导致工况1-3冲击区的测点应变大于工况1-4的冲击区测点应变。
2.2 位移分析
结构的位移可以直接反映结构在冲击过程中的变形规律,试验中记录了网壳结构部分关键节点的在冲击荷载下的动态位移。各工况下2个位移测点的最大位移值变化如图11所示,图11(a)为第1组试验工况下测点最大位移变化曲线,从工况1-1至工况1-3可以看出,随着冲击点数量的增多,D1、D2测点的位移逐渐增大,而工况1-4中测点D2位于冲击点处,导致D2位移剧增。图11(b)为第2组试验工况下测点最大位移变化曲线,工况2-1至工况2-2的变化趋势与第1组相同,但工况2-3由于测点距冲击点距离较远,位移与工况2-2中的位移相比并未出现明显变化,工况2-4由于D2测点距一个冲击点较近,导致测点位移剧增。与第1组相比,第2组由于冲击点外移,与测点相距较远,导致第2组测点位移整体小于第1组测点位移。
图11(c)为第3组试验工况下测点最大位移变化曲线,测点D2距冲击区距离比测点D1远,导致测点D2的位移波动较小;随着冲击同一径向杆的点数的增多,测点D1的位移逐渐增大。图11(d)为第4组试验工况下测点最大位移变化曲线,由于测点D1位于冲击点下,导致其位移明显大于测点D2的位移;其中工况4-3的3个冲击点位于测点D1的一侧,工况4-4的3个冲击点均匀分布在测点D1的两侧,较为集中,因而工况4-4测点D1的位移比工况4-3大。从图11可以看出,有限元的模拟结果与试验结果稍有差异,这是由试验误差引起的,但两者的整体变化趋势相同。
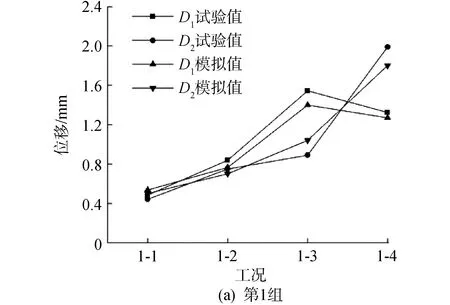
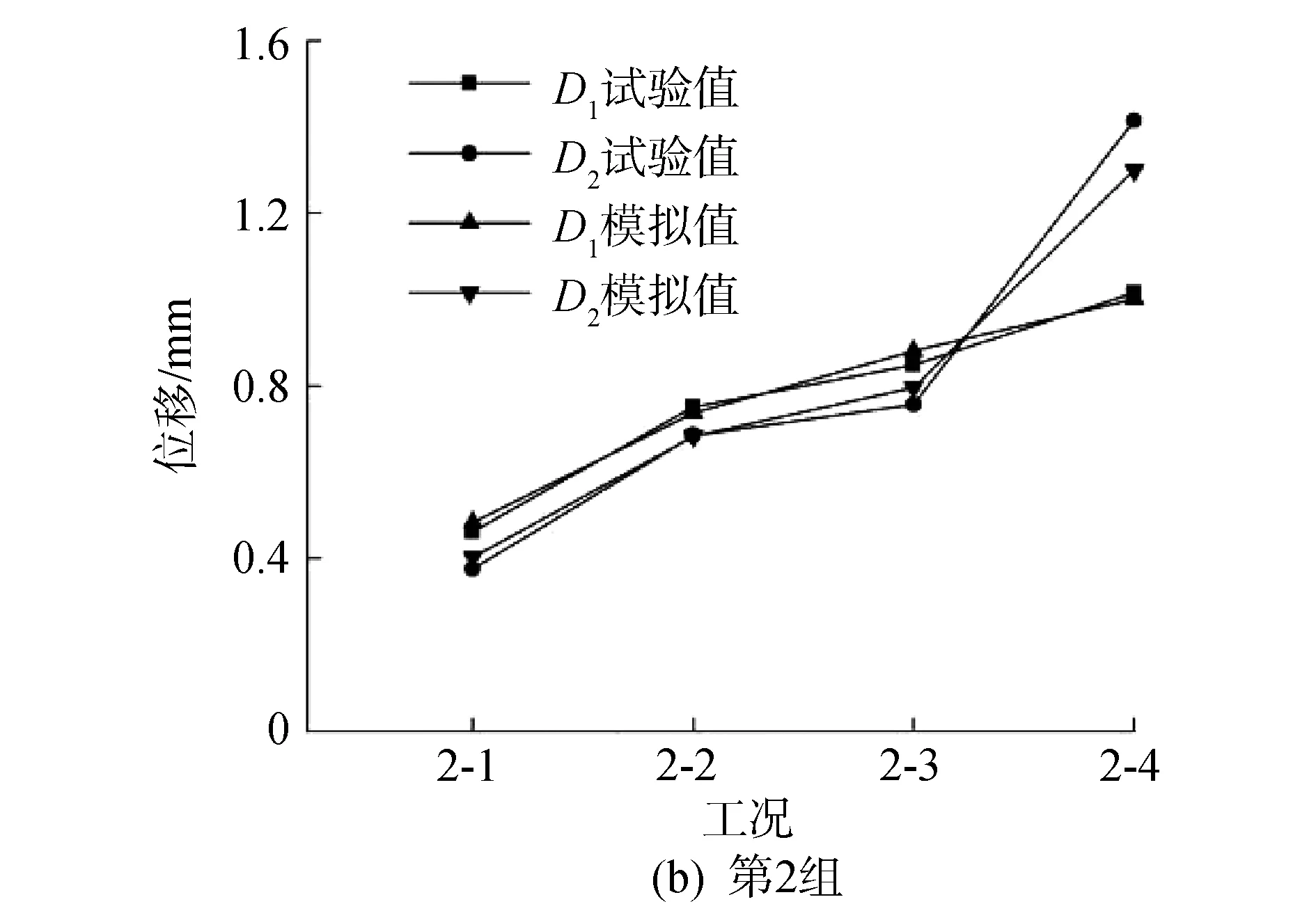


图11 工况位移峰值Fig.11 Displacement peak of the first group
2.3 加速度分析
加速度与结构的惯性力密切相关,是反映结构振动状态重要因素,为了研究加速度对网壳结构动力响应的影响,试验记录了网壳结构部分关键节点的加速度时程曲线。现对冲击点位于同一主肋杆的工况3-1至工况3-4的加速度时程曲线进行分析,其中A3加速度传感器安装于冲击区,A1、A2位于非冲击区。
图12~15为各工况加速度传感器的时程曲线图。随着冲击点逐渐增多,测点加速度值逐渐增大。工况3-2和工况3-3同为2点冲击,但工况3-2冲击点较为集中,并且在试验过程中,由于冲击球没有同时下落到结构上,导致A3加速度时程曲线出现2个明显峰值。

图12 工况3-1加速度时程曲线Fig.12 Acceleration time-history curve under condition 3-1

图13 工况3-2加速度时程曲线Fig.13 Acceleration time-history curve under condition 3-2
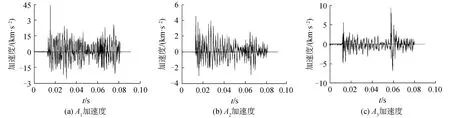
图14 工况3-3加速度时程曲线Fig.14 Acceleration time-history curve under condition 3-3

图15 工况3-4加速度时程曲线Fig.15 Acceleration time-history curve under condition 3-4
其中工况3-3加速度时程曲线中A1、A2、A3的第1次加速度峰值为4 404.9、4 533.7、5 583.3 m/s2,其中由于A3位于冲击区,A3加速度传感器第1次峰值加速度出现在0.013 s,而A1、A2位于非冲击区,导致A1、A2加速度传感器的第1次峰值加速度相对于A1滞后0.003 s左右;工况3~4加速度时程曲线中A1、A2、A3的第1次加速度峰值为5 423.9、5 100.7、11 078.7 m/s2,A3加速度传感器第1次峰值加速度出现在0.013 s,A1、A2加速度传感器的第1次峰值加速度相对与A1滞后0.005 s左右。从工况3-3到工况3-4冲击点由2个增加为3个,A1、A2、A3加速度峰值的增幅分别为23.13%、12.51%、98.40%,可以看出冲击点的增加会导致冲击区域的加速度发生较大增幅,非冲击区加速度增幅较小;而加速度传感器A1、A2之间的误差主要是由试验中传感器的安装位置发生偏移以及受空气阻力的影响导致冲击位置偏离冲击节点中心产生的。
2.4 试验现象与数值模拟
试验共4组,每组4个工况,均使用直径为100 mm的钢球从距离冲击点4 m高处释放,试验通过增加冲击点个数和变换冲击位置来研究K6型网壳结构的动力响应。试验结果显示,钢球冲击完成后,网壳结构在冲击点处有局部轻微凹陷,并且杆件与焊接球的连接部位有轻微变形,从而导致漆皮脱落现象,结构整体处于弹性阶段,无明显变形,能够继续承载。以工况1-1为例,图16中看出冲击点的最终变形,有限元模拟结果与实验结果较为吻合。

图16 工况1-1冲击点变形对比Fig.16 Deformation comparison of impact point under condition 1-1
冲击试验值和数值模拟结果值对比分析表明,测点响应的基本规律一致,误差在允许范围之内,验证了数值模拟的有效性,同时验证了网壳结构在多点弹性冲击荷载作用下的变形模式。以第1组工况为例,具体数据如表3所示。从整体来说,与模拟值相比,试验值偏小,其中加速度值误差范围为1.99%~12.45%,位移值误差范围为2.67%~16.85%。造成这些误差的原因是:

表3 第1组工况试验值与模拟值Table 3 Test value and simulation value of the first working condition
1)有限元模型为理想模型,但实际冲击试验时,网壳模型在加工厂制作时就存在一定的初始误差。
2)有限元模拟冲击时,冲击球能精准冲击到网壳结构的冲击点上,但实际冲击试验中,由电磁铁吸附的钢球在高空中存在微小摆动,导致冲击球下落到冲击点时冲击位置发生了偏差。
3 结论
1)随着冲击点数的增加,网壳冲击区域的应变、位移及加速度逐渐增加,网壳非冲击区域的应变、位移及加速度变化无明显规律且影响较小。在相同的冲击点数量及冲击速度下,冲击点位置对网壳结构的动力响应影响较大,冲击点越集中,网壳结构冲击区的应变、位移及加速度越大;网壳结构非冲击区域的应变、位移及加速度变化较小。
2)综合比较第1组试验工况和第2组试验工况,当冲击速度一定时,冲击点距网壳结构顶点越远,网壳结构冲击区的位移越小,顶点位移也越小。综合比较第3组试验工况与第4组试验工况,当冲击速度一定时,冲击网壳结构顶点时结构冲击区的位移较大。
3)冲击试验和数值模拟的结果基本吻合,变化规律一致,验证了数值模拟方法的有效性,同时验证了网壳结构在多点弹性冲击下的变形模式:冲击点处有局部轻微凹陷,冲击区杆件与焊接球连接处有轻微变形。
4)在网壳结构的抗冲击设计中,为避免结构遭受多点密集冲击和结构顶部遭受冲击时结构破坏,设计中应对结构顶部构件进行加强,并对冲击荷载下易破坏的关键杆件与节点的连接处做加强处理。
——以徐州高层小区为例

