非线性演化方程的切对称群分析
高晓润,黄晴
(西北大学数学学院,陕西 西安 710127)
1 引言
众所周知,李群理论是分析偏微分方程的一种通用和便捷的工具.它最主要的应用之一就是求解偏微分方程的不变解.因此,应用李群理论对偏微分方程进行群分类及进一步的精确求解问题引起了人们的广泛关注.只依赖自变量和因变量的变换,称之为点变换.更一般的,还依赖于因变量导数的变换,称为广义变换.特殊的,若变换依赖于自变量、因变量和因变量的一阶导数,则称之为切变换.目前,人们已经对点变换有了广泛且深刻的研究[1-2],而关于切变换的研究却比较少.
十九世纪数学家Sophus Lie(1842-1899)提出和发展了李群方法.此后,李群算法被认为是分析偏微分方程最强大的工具之一,主要原因是该方法可以减少变量数目,有可能导出与偏微分方程相关的群不变解,而且它也推动了其它数学物理方法的发展[3].
虽然关于广义对称的研究不多,但是近年来广义对称,尤其是切对称,受到了越来越多的关注.目前在切对称领域一些学者也做了许多工作.例如文献[4]使用二阶偏微分方程的切变换来求得这些方程的伪不变解.文献[5]将切变换应用于三阶常微分方程从而得到隐变换.在文献[6]中一些切变换也被认为是偏微分方程的隐对称的新起源.本文将优化系统的概念应用于切对称,提出一种代数分类算法.并以下面的二阶非线性演化方程为例:

给出它所容许的切对称并建立切对称的一维优化系统,然后进行对称约化,从而得到一些约化方程和群不变解.
众所周知切对称等价于一阶广义对称.
定理1.1[1]如果一个广义变换的无穷小生成子具有以下形式
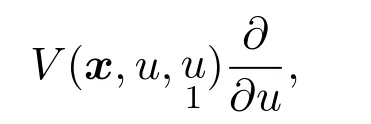
那么它等价于一个切变换且该切变换的无穷小生成子形式如下
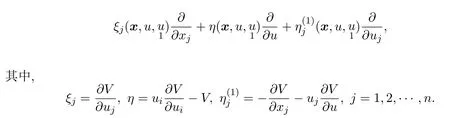
2 方程 (1)的切对称群分析
根据广义对称无穷小生成准则[1],可以得到方程(1)的切对称群.它由以下5个生成函数对应的向量场张成:
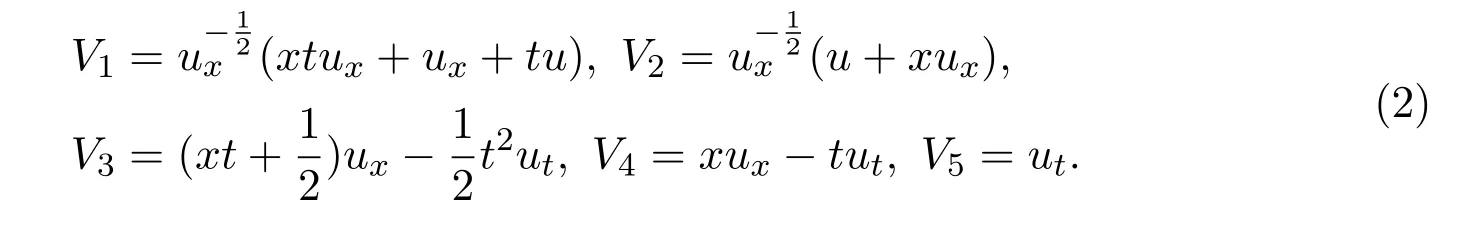
两个切对称生成子的交换关系由以下公式给出[7]

基于这个公式,计算V1,V2,···,V5之间的所有交换关系,并将结果列在表 1中,其中(i,j)项表示交换子[Vi,Vj].

表1 代数(2)的交换子表
伴随表示由李级数
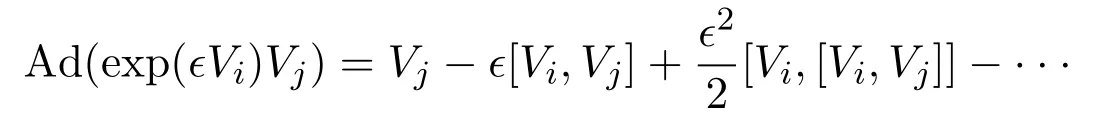
给出,其中[Vi,Vj]表示交换子(3),ϵ表示参数.表2给出了代数(2)的所有伴随表示,其中 (i,j)项表示 Ad(exp(ϵVi)Vj).
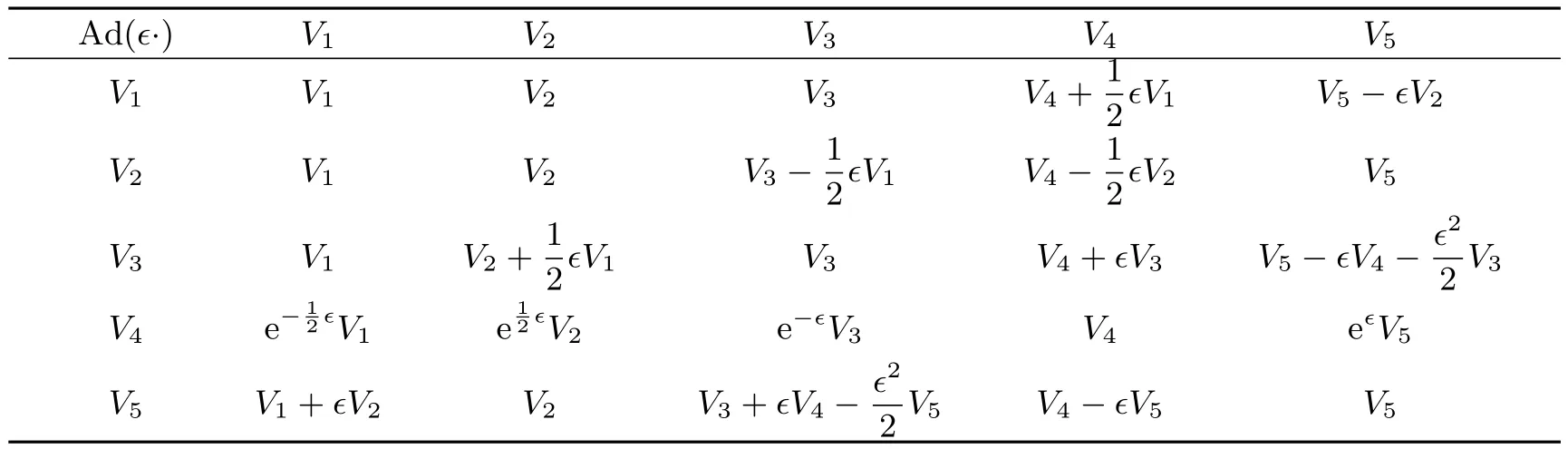
表2 代数(2)的伴随表示
给定方程所容许的切对称群有无穷多个子群,且任意无穷小生成子的线性组合还是无穷小生成子.为了能够不处理无穷多的切对称并完整准确地给出所研究方程的约化方程和不变解,需要得到切对称群的所有不等价子群,即建立切对称群的优化系统.
定理 2.1代数(2)的一维优化系统为
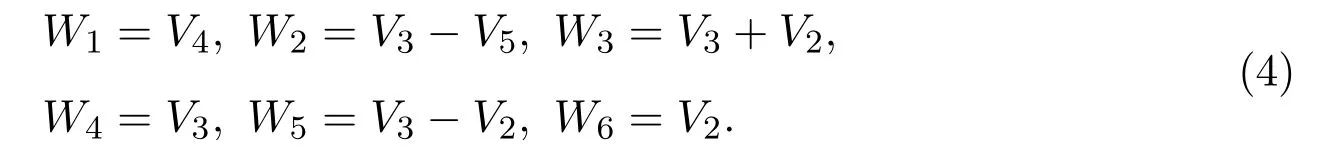
证明取V的最一般形式V=a1V1+a2V2+a3V3+a4V4+a5V5.接下来利用合适的伴随表示来简化它.将伴随表示Ad(exp(ϵ1V3))与Ad(exp(ϵ2V5))作用在V上,可以得到
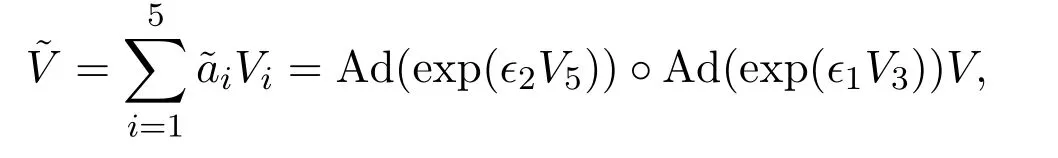


当令ϵ9=1,ϵ10=−2时,显然有V1与V2等价.所以可得V等价于V2.
现在已经证明了代数 (2)的任何一维子空间都等价于定理 2.1中由W1,···,W6张成的子空间之一.为了完成定理2.1的证明,将借助不变量或半不变量[8]来说明代数(4)中任意两个代数是相互不等价的.
引理 2.1是不变量.
证明通过计算,可以得到代数(2)的基灵型.易知在伴随作用下基灵型是不变的.
引理2.2定义

那么B,C是不变量.
证明从表2容易看出B与C是不变量.
现在,根据代数 (4)中的每一个Wi(i=1,···,6),可以确定不变量A,B和C,并将结果列在表3中.

表3 代数(4)的不变量
从表3易知每个Wi(i=1,···,6)都是不等价的.
3 方程(1)的对称约化和群不变解
此节将利用方程(1)的一维优化系统,对方程(1)进行对称约化,并给出相应的约化方程和不变解.
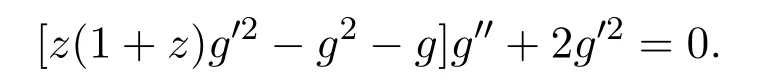
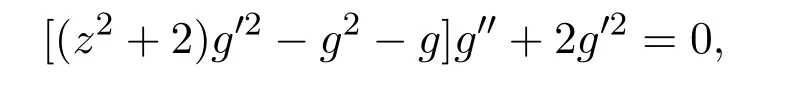
其中z=xt2+2x+t.
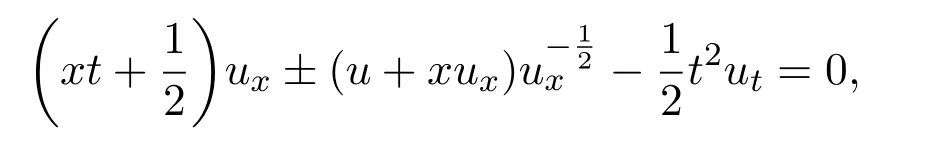
该情形中的方程求解比较困难,但是可以知道这是方程(1)的不变解在该分类下所必须要满足的条件.
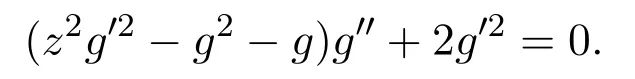
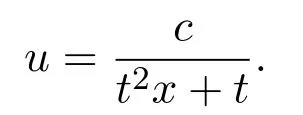
g′(t)=0.
因此有g(t)=c.故方程(1)有不变解
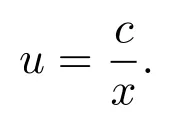
4 结论
本文研究了优化系统在切对称方面的应用,并以二阶非线性演化方程(1)为例,计算了它的切对称并建立了切对称的优化系统.然后根据优化系统中的等价分类,对方程进行了对称约化,并在此基础上获得了一些约化方程和精确解.
——与非适应性回归分析的比较
- 纯粹数学与应用数学的其它文章
- Persistence properties of solutions for an integrable two-component Camassa-Holm system with cubic nonlinearity
- Exact solutions of three classes of conformable time-fractional differential equations
- 非线性一阶边值问题正解的全局结构
- 两时滞广义Logistic模型的Hopf分支与混沌
- 扩散Beddington-DeAngelis捕食食饵模型的行波解
- 关于一些二进制数列的族复杂度和互相关测度

