蒙特卡洛模拟法在矿业项目净现值计算中的应用

卢皎旭，李角群，郭进平，程相琛，郑冰,

(1.西安建筑科技大学 资源工程学院，陕西 西安 710055；2.山阳秦鼎矿业有限责任公司，陕西 商洛市 726000)

0 引言

净现值（NPV）法是矿业项目经济评价中应用最广泛的方法之一，净现值是进行项目投资决策的一项重要指标[1-4]，其计算结果的准确性直接影响项目的投资。净现值计算受到矿石储量、贫化率、损失率、矿石的入选品位等诸多可变因素的影响。因此如何提高净现值的计算精度成了业内亟待解决的主要问题[5]。21世纪初吴爱祥教授首次将蒙特卡洛模拟法引入矿业项目的净现值计算中，并取得了良好的效果。但受制于当时计算机和相关软件功能的局限性，影响净现值计算结果的随机变量所服从的概率分布仍然是依靠历史经验来判断的[6-12]，模拟次数也是有限的，同时对于净现值结果的分析也仅仅只是从直方图中观察到大致的结果，并没有在一个确定的概率区间对其进行科学的分析[12]。为了解决上述问题，本文借助 Stata平台首先确定影响净现值计算的随机变量所服从的概率，之后调用Stata中的随机数发生器产生服从特定分布的随机数。最后实现对项目净现值进行蒙特卡洛模拟实验，并将计算结果以图表的形式输出；蒙特卡洛模拟法的引入解决了净现值计算过程存在的若干影响因素的随机性问题，实现了净现值计算的高效、快速、准确。

1 蒙特卡洛模拟法概述

蒙特卡洛模拟法也称为随机数模拟法，是一种基于已知随机变量产生特定随机数的模拟方法。其原理是利用影响目标问题的随机变量产生的若干随机数来代替相关变量参与目标问题的计算，因此需要首先确定相关随机变量所服从的概率分布，并利用Stata中的随机数发生器来产生相应的随机数。蒙特卡罗模拟法的步骤如下：建立相关问题的数学模型；产生若干特定的随机数；进行蒙特卡洛模拟实验并分析实验结果。

1.1 建立净现值（NPV）模型

矿业项目净现值计算过程中，需要充分考虑项目受内在因素以及外部条件等不确定因素的影响，如矿石的销售收入、销售成本、损失率、贫化率以及政府政策等，矿山的可服务年限、生产能力、销售收入、成本费用和采矿技术参数等。在实际的矿山项目经济评价过程中，既需要充分考虑其目标问题的影响因素，也要考虑计算的方便，因此建立数学模型如下。

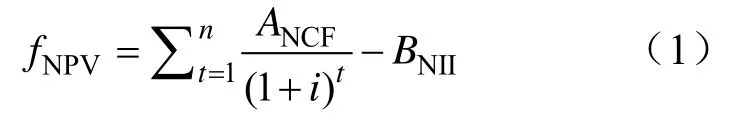
式中，fNPV为净现值；ANCF为净现金流量；i为基准收益率；BNII为项目初期投资额。

式中，X为矿产品销售收入；B为矿产品销售成本；D为折旧费；t为所得税税率。

式中，T为矿山的服务年限；A为矿山年产量；Q为矿床的工业储量；ρ为贫化率；η为采矿回采率。

需要注意的是，在计算矿山的服务年限时应该用废石混入率，但是由于混入的废石品位一般很低，而且具体数值不易确定，同时为了计算的简便，这里直接采用贫化率来代替废石混入率。同时矿产品的销售收入主要与矿山的产量和矿产品的价格有关；矿产品的产量又是由矿石的品位、回采率、贫化率共同决定的，所以净现值与上述影响因素密切相关。因此由公式（1）～（3）可得 NPV的计算模型如下：

1.2 产生特定概率分布的随机数

蒙特卡洛模拟的思想是：首先确定计算模型中若干随机变量的概率分布，其次通过 Stata中的随机数发生器来产生特定概率的随机数，参与 NPV的计算，最后通过调用相应的程序使得 NPV循环计算，并对实验模拟结果进行统计分析。

蒙特卡洛模拟的前提是产生相当数量的“随机数”，之后对模型中的随机变量建立抽样方法，实现从已知的概率分布抽样；由于各种概率模型都可以看成是由已知的概率分布构成的，因此产生特定概率分布的随机变量就成了实现蒙特卡洛模拟的重要方法。其中最简单、最直接的分布就是（0,1）分布，其他分布都可以看成是由（0,1）分布通过某种特定的方法转化而来，如利用“逆转方法”和“拒绝——接受法”来产生随机数[12]。

在实际应用中产生均匀随机分布随机数的方法有很多，但应用最广泛的是线性同余法生成随机数，公式如下：

式中，a为乘子；函数mod为求余函数；m为足够大的一个正整数。

使用该方法时必须给定一个初始值x0，也称种子值（Seed），而且种子值的选取须在1和最大值m之间。原则上参数可以根据自身需要设定，但是为了避免出现全周期情况，参数应按规则选取，才能使得生成的随机数满足问题的需要[8-9]。

生成相关随机数之后通过调用相关程序，将会对若干随机数进行统计分析，得出其平均值、标准偏差、最大值和最小值。之后采用“逆转方法”产生目标问题的随机数即可。

1.3 蒙特卡洛模拟实验

在产生相应的随机数之后进行蒙特卡洛模拟实验，通过编制相应的程序对项目净现值进行1000次的蒙特卡洛模拟实验。需要注意的是在模拟过程中是用“伪随机数”来代替随机数，最终将产生的伪随机数代入 NPV的表达式中进行计算，求解出1000次模拟实验的NPV值，最后对其进行统计分析。通过分析结果对项目净现值做出科学的判断，进而为项目的投资提供科学的支撑。蒙特卡洛模拟净现值计算过程如图1所示。

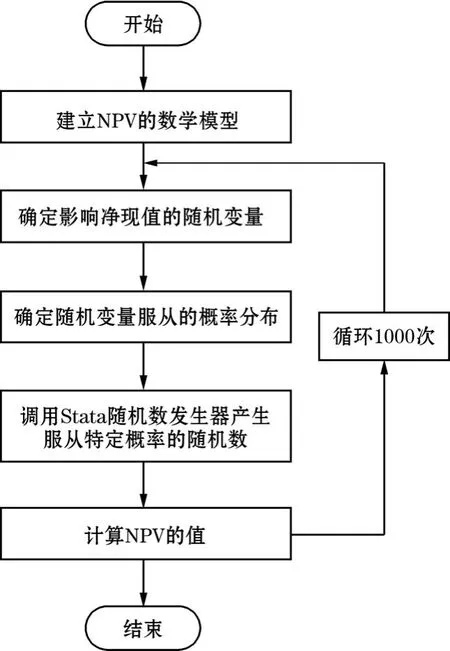
图1 基于蒙特卡洛模拟的NPV计算过程

2 工程实例

山阳秦鼎矿业公司设计前期露天开采，后期地下开采。项目预计 2025年全面建成，达产后黄金产量有望达到5 t以上。该矿山为国家级绿色矿山（试点）单位。截至 2019年底，矿山项目保有黄金资源储量为172 t，平均品位为1.99 g/t。矿山的详细资料见表1。

表1 秦鼎矿业公司相关地质资料

根据矿山相关资料，利用蒙特卡洛模拟法对项目净现值进行计算。

净现值法判断的依据是：若最终计算NPV≥0，则说明该项目风险较小，是可以接受的；若NPV＜0，则说明该项目风险较大，是不可以接受的。

由公式（4）可知随机变量有A、Q、ρ、α等。对该矿山相关变量进行统计，结果见表2。

对表2中矿床工业储量Q进行统计分析和正态性检验，如图2所示。由图2可知，矿床的工业储量随时间变化的曲线服从N（172，5.22）的正态分布。对该矿山矿石入选品位α进行统计分析和正态性检验，如图3所示。由图3可知，矿石入选品位随时间变化的曲线服从N(1.99，0.012)的正态分布。对该矿山的矿石销售价格γ进行统计分析和正态性检验，如图4所示。由图4可知，矿石的销售价格随时间变化的曲线服从 N（362.34，5.22）的正态分布。对矿石的销售成本c进行统计分析和正态性检验，如图5所示。由图5可知，矿石的销售成本随时间变化曲线服从N(176，3.22)的正态分布。并对折旧费、所得税率、矿山的年产量、采矿回采率、矿石回采率等进行统计分析和正态性检验，结果均不服从正态分布。

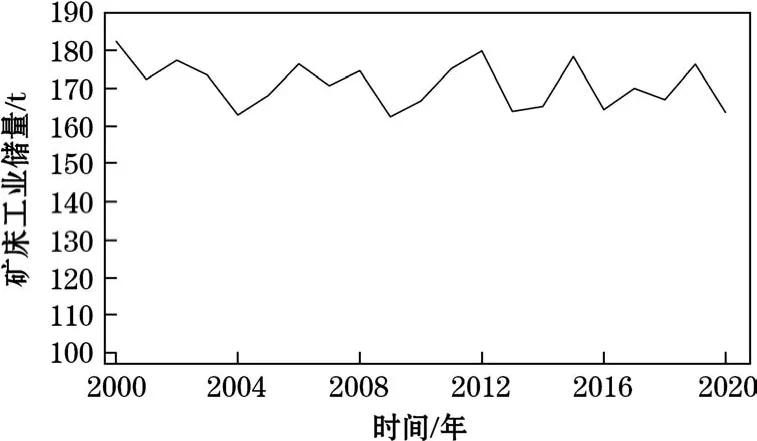
图2 矿床工业储量变化规律

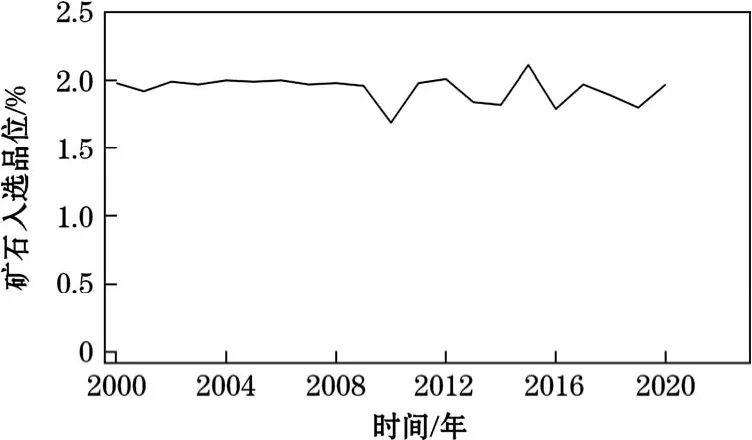
图3 矿石入选品位变化规律

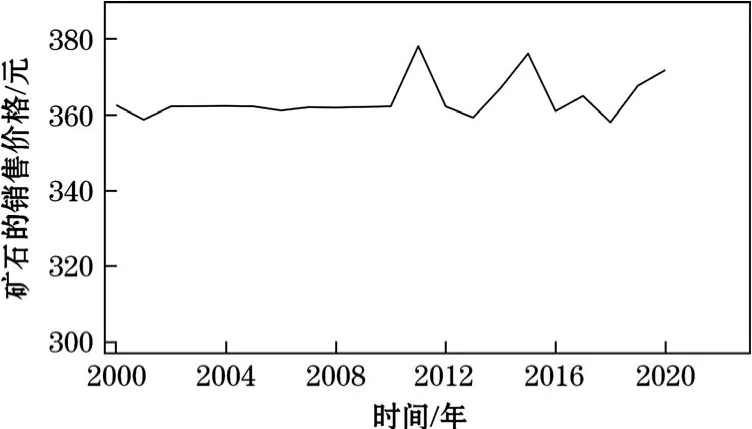
图4 矿石销售价格变化规律

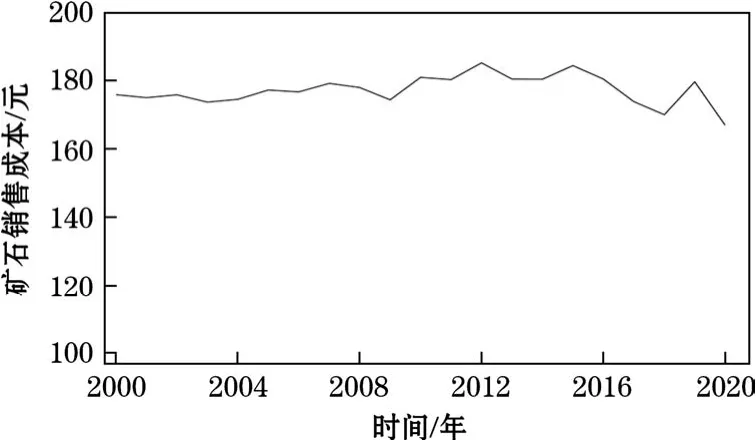
图5 矿石销售成本变化规律

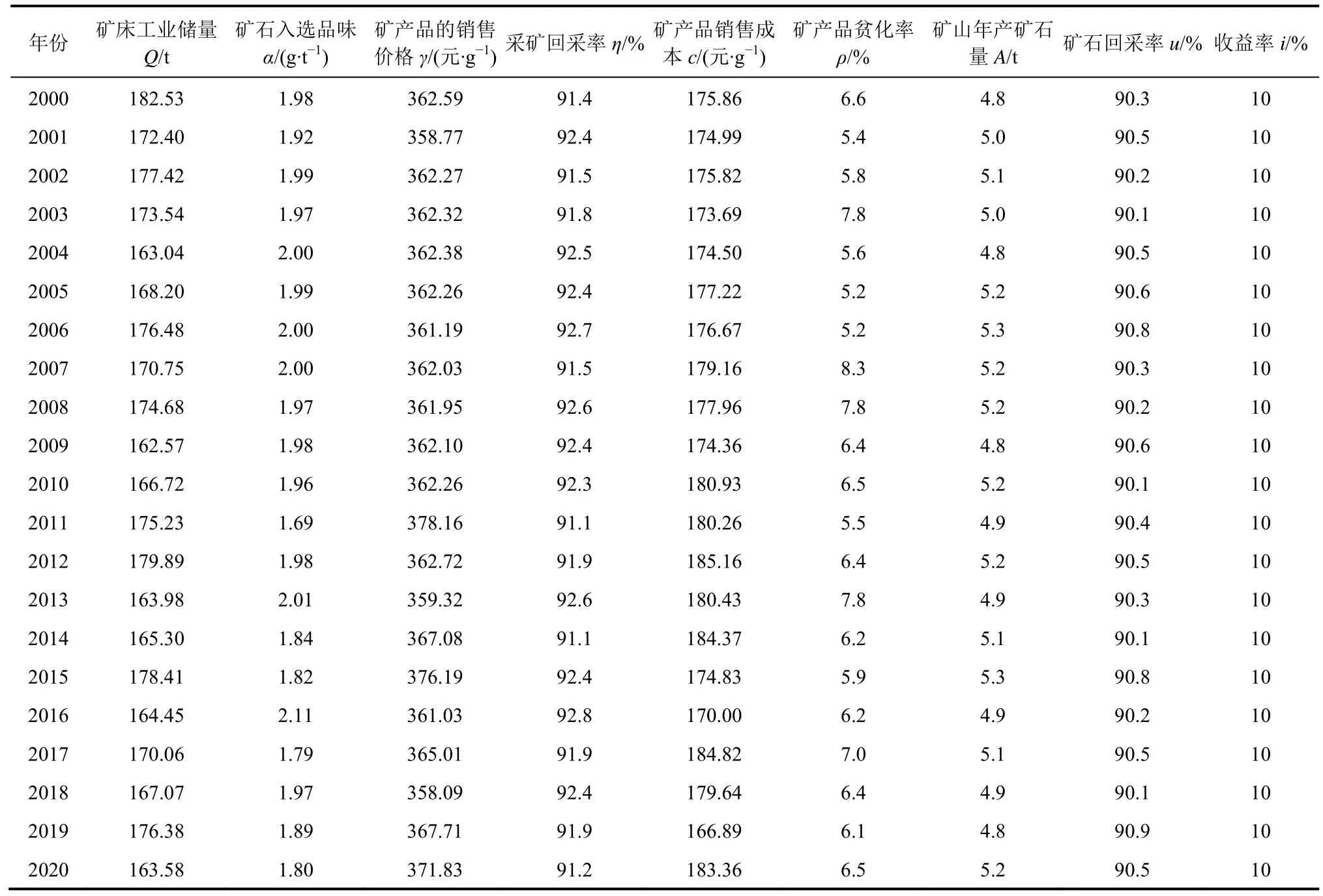
表2 秦鼎矿业2000-2020年相关参数

在 Stata中通过编制相应的程序计算基于若干随机数变量的NPV，之后再对蒙特卡洛模拟得到的1000个净现值进行统计分析，从总体上对项目净现值做出判断，为项目的评价提供科学的支撑。

其原理如下：对于模型中的每一个随机变量进行一次模拟计算需要一个随机数参与；而每产生一个随机数，对应就产生一个净现值，本次模拟实验进行1000次，也就产生了1000个对应的随机数和1000个净现值。最后对模拟结果进行统计分析，如图6所示。

由图6可知，该项目的NPV均值为3 756 799元，最大值为3 800 265元，最小值为253 456元，均大于 0，说明该项目在理论上是可行的；之后基于这1000次模拟的净现值样本在98% 的置信区间对其进行分析，结果见表3。由表3可知，该项目净现值均值分布范围为（3 712 543, 4 001 055），也就是说净现值均值落在（3 712 543, 4 001 055）上的概率为 98%，再次验证该矿山项目的投资是可行的。

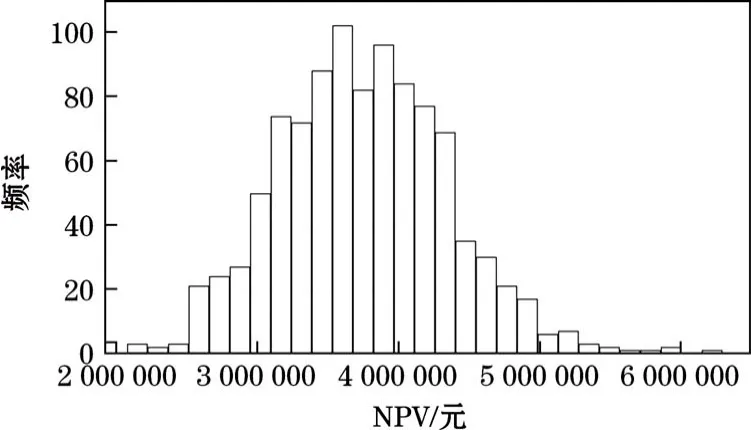
图6 蒙特卡洛模拟1000次的净现值频率分布直方图

表3 模拟1000次的净现值在98%置信区间分析结果

3 结论

（1）在Stata中既可以确定随机变量服从的概率分布，也可以直接对 NPV进行蒙特卡洛模拟实验，并将计算结果以图表的形式输出，从图表中可以直观看出净现值的相关情况，为项目经济性评价提供科学的支撑，具有较强的可操作性和实用性。

（2）基于蒙特卡洛模拟的净现值NPV计算，充分考虑了“随机变量”对 NPV的影响，完善了以往在其计算过程中对变量的处理方法，同时在98%置信区间对模拟结果进行统计分析，使得结果更加合理可靠。

（3）蒙特卡洛模拟法的实质是基于已知随机变量产生特定随机数的前提下进行的，因此实验的可靠性与相关随机变量服从的概率分布准确与否有关，若随机变量服从的概率分布有偏差，则可能导致实验结果存在较大误差。