近地小行星(10302) 1989 ML和(4660)Nereus的轨道特征及演化分析∗

陈媛媛 马月华

(1 中国科学院紫金山天文台南京 210023)

(2 中国科学院行星科学重点实验室南京 210023)

1 引言

近地小天体(Near-Earth Object,NEO)作为一种特殊的小行星群,是指其轨道近日点小于1.3 au的小行星及彗星.近地小天体是离地球最近的一类天体,这种距离优势使其成为进一步了解太阳系、发展优化深空探测项目以及开发太空资源的首选目标.同时它们潜在的碰撞威胁也让我们不得不对其进行更加严密的追踪和观测.一般认为近地小天体是“离群”或碰碎的主带小行星和“熄火”彗星的组合群[1],如此多样性的来源使其可以与太阳系不同区域的天体相互对接寻找演化线索.同时,近地小天体还是陨石的最主要来源地之一,从而也能与行星化学中的陨石分析和统计进行间接对比和佐证.对近地小天体轨道的动力学研究是其中的重要组成部分,为地面观测及探测项目提供了必不可少的理论支撑,也为小行星撞击事件的预警提供关键的预报和筛查.

近地小天体的动力学研究本身存在不确定性,但在实际应用中又需要高精度的定量结果,从而使其成为一个相对困难的研究方向[2].这一动力学研究方向的不确定性是多方面的.首先,大多数小行星身处混沌的相空间之中,任何方面的细微不同都会导致生成的模拟轨道与其实际轨迹大相径庭.其次,大多数小行星的观测数据本身存在误差,同时即使观测误差足够小,由于观测弧段太短导致的定轨误差也不容忽视.再次,力模型的选择非常重要,在尽可能精细的力模型与尽量减少计算机的截断误差之间需要谨慎权衡.

近地小天体作为一个族群,其整体的动力学起源至今仍没有定论.通过稳定性分析及数值模拟发现,这些小天体的平均年龄只有百万年量级,所以需要一种机制持续不断地对这个小行星群进行补充,使其在当前太阳系整体稳定的状态下保留至今.普遍认为,近地小天体的起源地有两个:主带小行星和彗星[3–5].主带小行星在µ6长期共振、木星的3:1、5:2、2:1等主要平运动共振以及其他共振的摄动作用下增加偏心率,引发与火星的密近交汇,从而散射到近地球的区域,这一过程仅需要几十万年.不过这些作为“供应源”的共振区也需要有后续材料的补充,Yarkovsky效应引起的半长轴长期变化可能在其中起了决定性作用,但相关研究还处于假设和理论推理阶段,并没有观测方面的验证.而对于彗星起源,由于其起源地的小行星大小分布不明以及轨道演化中受到不确定的非引力作用,导致数值模拟从彗星演变成NEO比较困难.在文献[3]中,作者将NEO的源区域分成5个部分:µ6共振区、与火星交汇的中转区、木星的3:1共振区、外主带小行星以及越海王星盘(Transneptunian disk),给出了绝对星等H <22的小行星来自不同源区域的比例,指出其中大约6%来自木星族彗星,远小于来自主带小行星的比例.他们同时估计了Amors、Apollos和Atens 3类近地小行星在整体NEO中的占比.

1989 ML的轨道半长径为1.27 au,具有中等偏心率～0.136,较小轨道倾角～4.4°.作为近地小天体,由于空间探测所需能量很少,所以一直是交汇类探测任务(rendezvous mission)的首选目标[6].Binzel等人于1999年3月和5月利用帕洛玛天文台的5 m Hale望远镜对1989 ML进行了0.3–0.9µm的光谱观测,并推测其光谱特征与黑色球粒陨石最接近,即一种在碰撞冲击作用下变暗的普通球粒陨石[7].Mueller等人同时利用Spitzer望远镜的红外成像摄像机(IRAC)和2.0 m Faulkes望远镜(北)对1989 ML进行了红外、近红外及光学波段的测光观测.通过对观测数据的分析及模型处理,得出1989 ML的有效直径为(0.28±0.05)km,几何反照率为0.37±0.15[8].

(4660) Nereus (1982 DB)小行星轨道半长径～1.49 au、偏心率～0.36、轨道倾角更小～1.43°.同样地,由于其轨道倾角很小,从而对交汇类任务而言所需能量较其他大多数小行星更少.Nereus在2002年1月曾与地球有一次密近交汇,最近距离达到0.029 au.在这次回归期间,美国宇航局3 m口径红外望远镜(IRTF,位于夏威夷)、美国帕洛玛天文台的5 m Hale望远镜、亚利桑那州基特峰国家天文台的4.0 m Mayall望远镜、夏威夷10 m Keck-I望远镜、欧洲南方天文台3.5 m新技术望远镜(NTT,位于智利)以及两个著名的雷达设备Arecibo、Goldstone都对其进行了专门的观测.Delb´o等人利用夏威夷10 m Keck-I望远镜测量了Nereus在8–18µm波段的红外热流量,并利用标准热模型(STM)、快速自转模型(FRM)以及近地小行星热模型(NEATM)对观测数据进行模拟对比,得出Nereus的直径～0.33 km,反照率较高为0.55±0.17[9].Binzel等人结合IRTF、Hale和Mayall 3个望远镜的数据,给出了0.3–2.5µm波段Nereus的光谱,并将其光谱斜率及其吸收特征与其他小行星相对比,将其归为Tholen分类系统中的E型小行星.同时根据0.49µm处的光谱特征推测其与顽火辉石陨石(enstatite achondrite meteorites/aubrite)有关,起源于位于内主带有较高整体倾角的Hungaria群[10].但不像另一颗E型小行星(3103) Eger,其轨道倾角与Hungaria群的平均水平相当,Nereus的超低倾角似乎很难从Hungaria群的小行星演化而来.这个差异使Nereus的真正起源变得模棱两可.Lazzarin等人利用NTT得到0.4–1.65µm范围的光谱数据,并将其与顽火辉石陨石光谱相对照,结果相当吻合.他们还断言,Nereus可能是很久之前从Hungaria群演化而来,其轨道倾角的差异源于ν16共振(可以看成是小行星的升交点经度与土星的升交点经度之间的耦合)[11].Brozovic等人分析了Arecibo、Goldstone两个雷达设备根据2002年Nereus最接近态的观测影像,给出了较精确的形状轮廓(3轴方向分别为(510±20)m、(330±20)m、)以及自转轴在黄道极坐标系的指向(黄经λ=+25°±10°、黄纬β=+80°±10°)[12].Nereus将于2021年12月再次接近地球,并且其最近距离较2002年更近,可达0.026 au.

针对近地小行星的轨道动力学演化已有的研究工作列举如下:文献[13]对这两个小行星前后几千年的轨道演化进行了数值模拟,并得出结论:1989 ML的轨道是混沌的,因此只能得到大约1000 yr以内的精确轨道,而Nereus的轨道更混沌,只能得到200 yr内的轨道;文献[14]讨论了研究近地小行星所需要的动力学模型选择问题,并给出了2000–2100年内6个近地小行星与地球的密近交汇信息,其中包括Nereus;文献[15]和[16]提出近地小行星可以短暂地进入木星的3:1和1:1平运动共振,这可使其轨道暂时地避开密近交汇而保持稳定.同时列举了与大行星发生长期共振或Kozai共振的情况;文献[17]列出了24个近地小行星在2000–2100年内与地球的密近交汇信息,并给出了13个近地小行星1万年内轨道各根数的变化范围,其中均包含小行星Nereus;文献[18]数值模拟了(433)Eros和(4660) Nereus两个近地小行星向后2 Myr内的轨道运动,并针对5个Nereus的克隆轨道详细讨论了其与各大行星密近交汇及发生各种共振的情况.他们指出,Nereus的轨道演化主要由与地球的密近交汇所主导.

本文利用最新的轨道初值,在其观测误差范围内各取了1000个克隆粒子,更加系统地研究了1989 ML和Nereus这两个近地小天体的轨道稳定性及相关动力学特征.内容安排如下:第2部分对本文使用的数值模拟方法及初值选取做了详细的说明,第3部分从稳定时标、可能的运动范围、密近交汇及各共振对轨道的影响等方面做了详细的讨论,并将两个小行星的结果作比较.第4部分给出主要结论.

2 方法及初值设置依据

2.1 力模型及积分器

本文利用N体运动来研究在太阳系主要引力作用下两个小行星1989 ML和Nereus的轨道运动.本文考虑的N体动力学模型包括八大行星、冥王星系统(系统质心运动)、月球以及4个最大的小行星(Ceres、Vesta、Pallas和Hygiea).以上包括太阳在内的15个天体均是考虑质量的大天体,而两个小行星则忽略其质量,为测试粒子.天体的相对论效应、非球形效应以及其他非引力效应(太阳光压及Yarkovsky效应等)均被忽略.

模拟程序主要使用Mercury程序包中的BS(Bulirsch-Stoer)算法[19],同时用RKF7(8)(Runge-Kutta-Fehlberg)积分器进行对比和精度验证.积分中设置精度为10−15,对比计算前后系统的总能量之差∆E与总角动量之差∆L,计算10万年后两种算法的截断误差比例分别为∆E≈10−11,∆L≈10−11(Mercury中BS算法)和∆E≈10−13,∆L≈10−13(RKF7(8)积分器).

2.2 初值设置

本文中的初值使用的是JPL(Jet Propulsion Laboratory)中Horizons给出的根数,所有大天体取简化儒略日MJD59000.0 (Modified Julian Day)时刻的瞬时根数,具体数值见表1.表中G为引力常数、MP表示天体质量、a是轨道半长径、e为轨道偏心率、i为轨道倾角(行星轨道面与黄道面夹角)、ω为近点角距、Ω为升交点经度、M为平近点角.各大天体在各个时刻的位置均由初始瞬时根数和N体模拟计算得出,并没有利用更多的即时观测数据,因此大行星在程序计算里的位置与实际历表位置的差值也可能导致小行星轨道的误差,比如水星在相对论作用下的近心点进动.由于本文着重点在于小行星1989 ML和Nereus的轨道特征及演化的定性研究,而并非得出针对工程的精确历表的定量结果,所以上述力模型和初值可视为相对的合理设置.

表1 本表列出了数值模拟中用到的所有大天体的初始值, 为MJD59000.0时刻的瞬时根数.数据来源: https://ssd.jpl.nasa.gov/Table 1 This table lists the initial values of all major objects used in the numerical simulations, which are the instantaneous elements at M JD59000.0.Data sources: https://ssd.jpl.nasa.gov/

表1 续表Table1 Continued

小天体的标称轨道选在其各自已知观测时段中间时刻对应的瞬时轨道(来自近地天体动态网站(Near Earth Objects Dynamic Site,NEODyS)),因为此刻的轨道是相对而言限制条件最优的[20],分别对应儒略日JD=2455061.9 (1989 ML)和JD=2457165.8(Nereus).各轨道根数的具体值见表2和表3.在Mercury程序计算中,首先把它们积分到跟大天体一致的时刻再一起计算.

2.3 克隆粒子的选取

为了对观测误差范围内两个小行星可能的动力学特征做进一步的研究,我们利用NEODyS中给出的小天体轨道根数和对应协方差矩阵[21]1NEODyS中给出的小天体轨道根数有效数字太少,而Horizon中最小步长被限制为1 d.为了提高精度,对a、e、i、ω、Ω 5个根数实行Horizon中相邻两个瞬时根数的线性插值.平近点角M还是取的NEODyS给出的原值.,根据多元正态分布分别为两个小行星选取了1000组邻近的轨道根数作为其克隆粒子.

3 主要结果

本节首先从小行星的稳定性讨论出发,利用最大Lyapunov指数(MLE)与MEGNO指数(Mean Exponential Growth factor of Nearby Orbit)给出小行星目前轨道的Lyapunov时间.其次,通过对克隆粒子的统计,给出10万年内小行星的可能运动范围以及在此时间段内与大行星的密近交汇及碰撞情况.最后,针对其标称轨道,分析了对轨道有重要影响的各种共振.

3.1 最大Lyapunov指数与MEGNO指数

这两个指数都是需要在N体演化的过程中计算的.MEGNO指数在Lyapunov指数的基础上发展而来,平均MEGNO指数随时间变化的斜率即对应最大Lyapunov指数.在大多数情况下相比Lyapunov指数,MEGNO指数可以更快地收敛到极限值[22],计算效率较高,因此常用于相空间的扫描.计算用到的微分方程表达式见附录.

模拟过程中对初始轨道距离d0和正规化时间间隔δT两个参数的说明如下:

•由于MLE和MEGNO的大小衡量了某轨道附近轨道随时间推移的偏离程度,在计算的初始设置中需要首先设定一个轨道距离d0.本文中d0的具体设置如下:分别以小行星的标称轨道和6个轨道根数1−σ误差处(均取加号)对应的轨道求其相对于太阳的位矢,两个位矢之差取模作为d0.同时计算了轨道根数最大误差取减号时与标称轨道之间的位矢差作d0的情况,发现d0的变化并没有对指数的演化结果产生本质影响.

•为了避免轨道演化过程中轨道距离向量δ随时间快速增长以致溢出,需要在固定的时间间隔δT内对其进行正规化.δT越小,上述指标在时间演化过程中的稳定性越好[23].基于稳定性以及计算效率的考虑,本文计算中设置了δT=3 yr.

图1给出了在太阳系主要动力系统背景下1989 ML小行星的MLE、Y及〈Y〉随时间的演化.由图可知,1989 ML的MLE～10−2.4,对应Lyapunov时间TL～251 yr,与文献[24]中给出的TL=226.2 yr相当.图1(c)中〈Y〉的斜率即对应最大Lyapunov指数值,与图(a)中的MLE值一致.

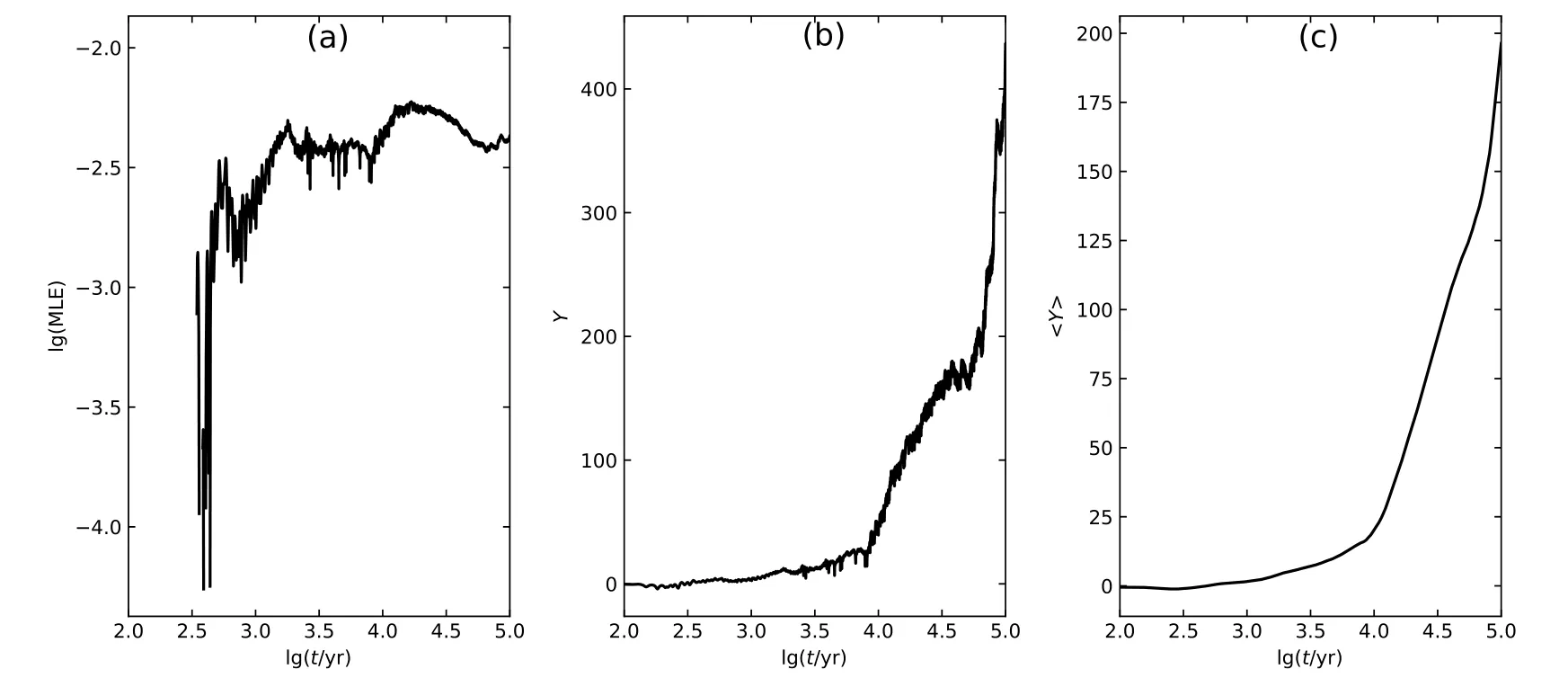
图1 1989 ML标称轨道的最大Lyapunov指数、MEGNO指数Y 及平均MEGNO指数〈Y〉随时间t的演化Fig.1 Time evolution of the maximal Lyapunov exponent,the MEGNO Y and the average MEGNO 〈Y〉of the nominal orbit of 1989 ML

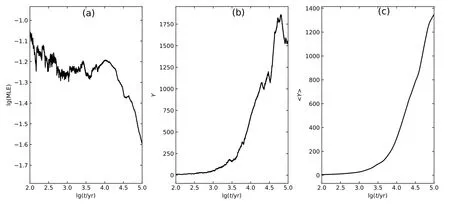
图2 Nereus标称轨道的最大Lyapunov指数、MEGNO指数Y 及平均MEGNO指数〈Y〉随时间t的演化Fig.2 Time evolution of the maximal Lyapunov exponent,the MEGNO Y and the average MEGNO 〈Y〉of the nominal orbit of Nereus

用相同方法计算了Nereus的上述两个稳定性指标,发现在演化了10万年之后,MLE仍没有收敛.这是由于此小行星的轨道极其不稳定,其半长径相比初值已经变化很多,从而导致其轨道在相空间中的位置不断变化.这也说明这两种指标在衡量天体稳定性方面对N体运动(N >3)中极其混沌的轨道并不适用[23].我们只能从前1万年的演化中提取出一个MLE的近似值～10−1.25,对应TL～18 yr.与其相比,文献[24]中给出的TL=41.8 yr,文献[25]中给出的TL=23 yr.这其中的差别一是由于Nereus的轨道极不稳定,二是由于MLE这种稳定性指标只能作量级上的参考,具体的精确值并无意义[26].

3.2 运动的可能范围区间

本小节通过统计1000个克隆粒子的运动轨迹得到1989 ML与Nereus两个小行星在10万年内的可能运动范围.

固定输出间隔100 yr,在每个输出时刻取所有克隆粒子各轨道根数的最大和最小值,得出小行星可能的运动范围,如图3和图4所示.从中可以看出,小行星1989 ML在前后10万年内a∈[1.25,1.3]au附近,e∈[0.1,0.21],i∈[0°,8°],轨道可能区间在其标称轨道附近.而小行星Nereus在前后10万年a∈[1,2.2]au范围,已超出火星轨道到达主带小行星区域;e∈[0.1,0.6],i∈[0°,10°],如此大的范围也反映了其轨道极端混沌.

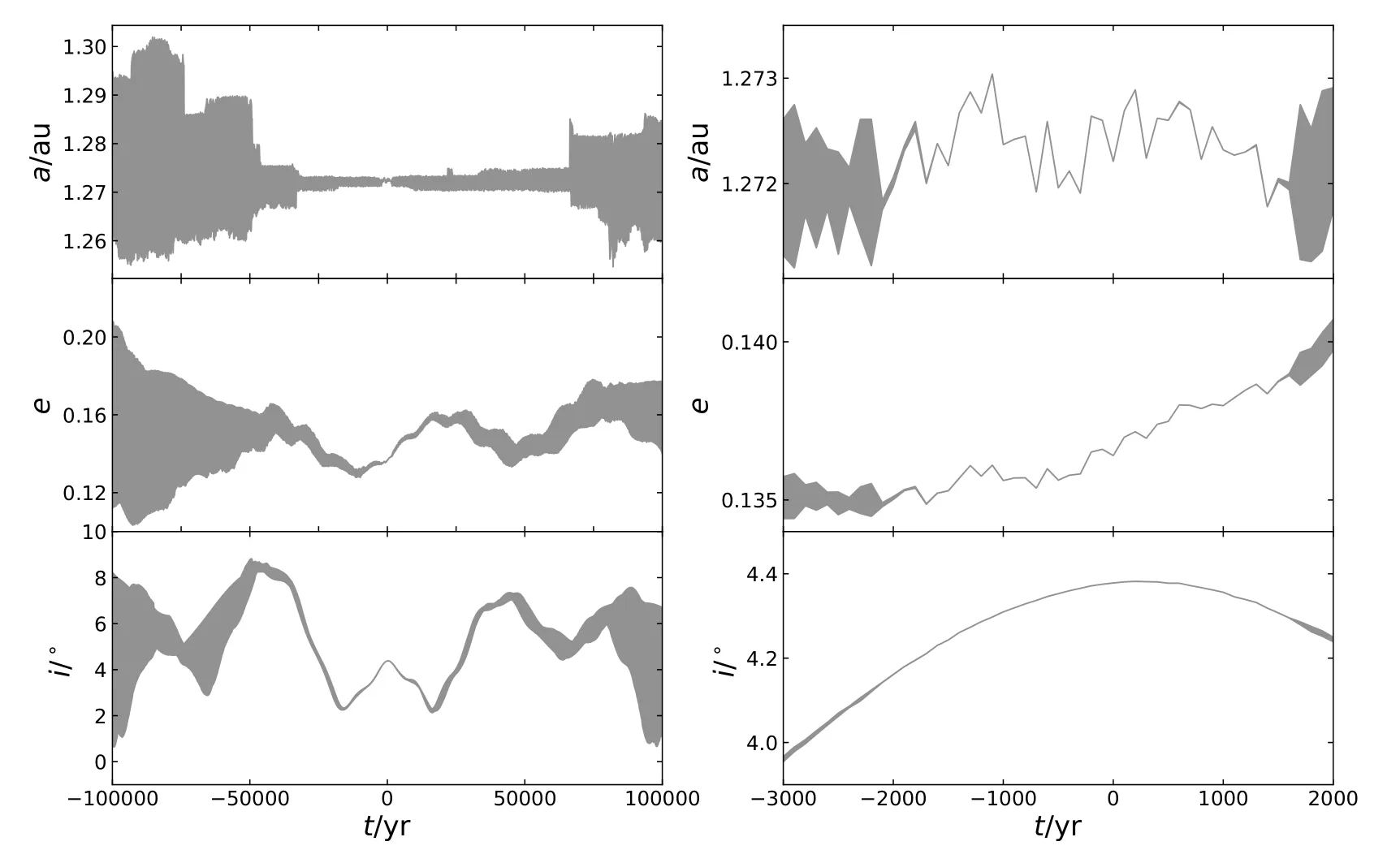
图3 1989 ML在前后10万年(左图)及[−3000,2000]年内(右图)的可能运动范围Fig.3 Possible moving ranges of 1989 ML within 0.1 Myr forward and backward (the left panel) and within the time interval [−3000,2000] yr (the right panel)

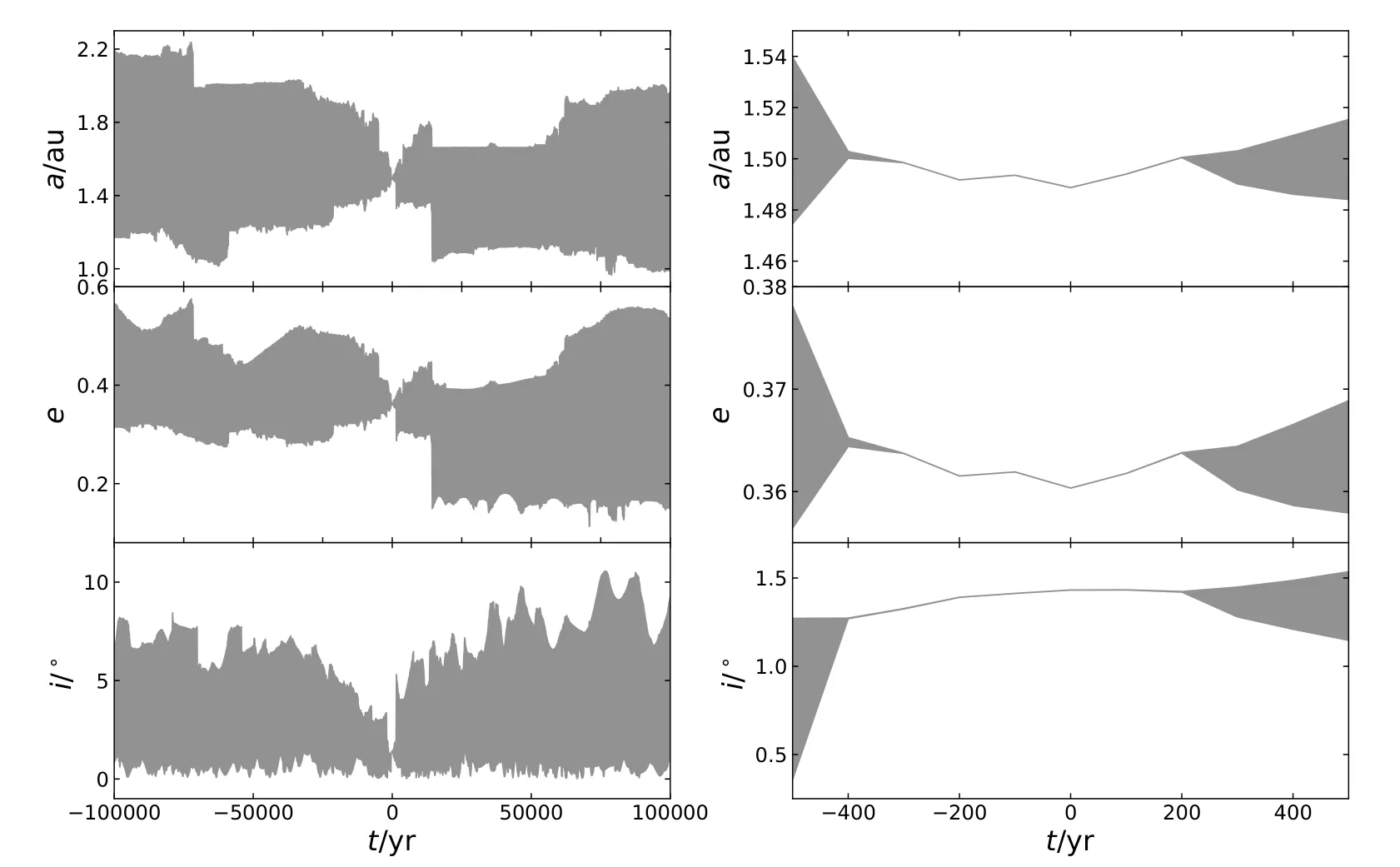
图4 Nereus在前后10万年(左图)及500 yr内(右图)的可能运动范围Fig.4 Possible moving ranges of Nereus within 0.1 Myr forward and backward (the left panel) and within 500 yr (the right panel)

图5给出前后10万年内两个小行星的各1000个克隆粒子在a-e相空间内的出现概率分布图.图像是这样得出的:先根据小行星半长径和偏心率的可能范围取固定的区间(对1989 ML,a∈[0.65,1.8]au,e∈[0.0,0.5];对Nereus,a∈[0.5,2.8]au,e∈[0.0,0.85]),将每个区间分成200等份,对所有200×200个2维区间,记录落在每个区间输出值的次数.

由图5(上)可以看出,1989 ML在a-e图中的集中分布区域垂直于a轴,表明小行星1989 ML目前所处相空间起主导作用的为平运动共振.图中用红色虚线标出了小行星的标称轨道与类地行星的主要平运动共振位置,分别为水星1:6、金星3:7、地球7:10和火星25:19.第3.4节还将对此做详细的讨论.与此相对应,图5(下)中显示的Nereus的a-e分布图集中分布区域则沿着与地球轨道相交线的内边缘,这表明Nereus所处的相空间中,与地球的密近交汇及碰撞起到了主导作用[1],这与文献[18]的结论是一致的.通过分布图还可以看出近地小行星的克隆粒子在金星、地球和火星的特洛伊小行星、处于各平运动共振的小行星(图中垂直于a轴的细长区域)以及高偏心率的主带小行星在这些区域均有出现,说明这些区域与近地小行星当前的相空间都是高度联通的,这也喻示了这些不同族群的小行星之间相互迁移转化的可能性.

图5 1989 ML (上图)和Nereus (下图)前后10万年内在半长径-偏心率相空间中的分布图.以100 yr为输出时间间隔,图中颜色表示lg(X +1),其中X为粒子落在某区域的次数,+1是将次数为0的区域变为1,从而取对数时为0.图中黑色实线划出了与地球轨道相交的范围,线上为可相交区域,黑色虚线为与火星轨道相交范围.红色实线为金星、地球、火星的轨道位置(从左向右),红色虚线为行星的平运动共振位置,E 7:10为地球的外7:10共振,Ma 25:19为火星的内25:19共振,V 3:7为金星的外3:7共振,Me 1:6为水星的外1:6共振,4个共振从上到下依次对应从左向右的红色虚线.红色圆点代表小行星当前位置.Fig.5 The distribution of 1989 ML (top) and Nereus (bottom) in the semi-major axis versus eccentricity phase space within 0.1 Myr forward and backward.Taking 100 years as the output time interval,the color in the figure represents lg(X +1),where X is the number of times a particle falls in a certain area,and+1 is to change the number of times 0 into 1,thus taking the logarithm as 0.In the figure,the black solid lines limit crossing areas with the orbit of Earth,above the line is the crossing area,and the black dotted line with the orbit of Mars.The red solid lines show locations of Venus,Earth and Mars (from left to right),and red dotted lines are mean motion resonance spots with planets,E 7:10 means outer 7:10 resonance of Earth,Ma 25:19 inner 25:19 of Mars,V 3:7 outer 3:7 of Venus,Me 1:6 outer 1:6 of Mercury,the four resonances from top to bottom correspond to the red dotted lines from left to right.The red dot represents current position of the Asteroids.

3.3 密近交汇与碰撞概率统计

本小节统计了1989 ML前后50万年内和Nereus前后10万年内与地球、月球、金星及火星的密近交汇及碰撞概率.

通过图6可以看出,1989 ML在前后10万年内与地球发生密近交汇的概率很小(<0.1%),前后10万年内的密近交汇均是与火星发生的.而与地球的密近交汇在10万年后发生,并且随着时间呈递增趋势.在20万年之后还会发生与月球和金星的密近交汇,次数也是随时间递增的.通过对交汇最小距离的统计得知,50万年内进入地球和火星0.1个Hill半径的次数相当,同时随着最小距离的增加,交汇次数呈递增趋势.

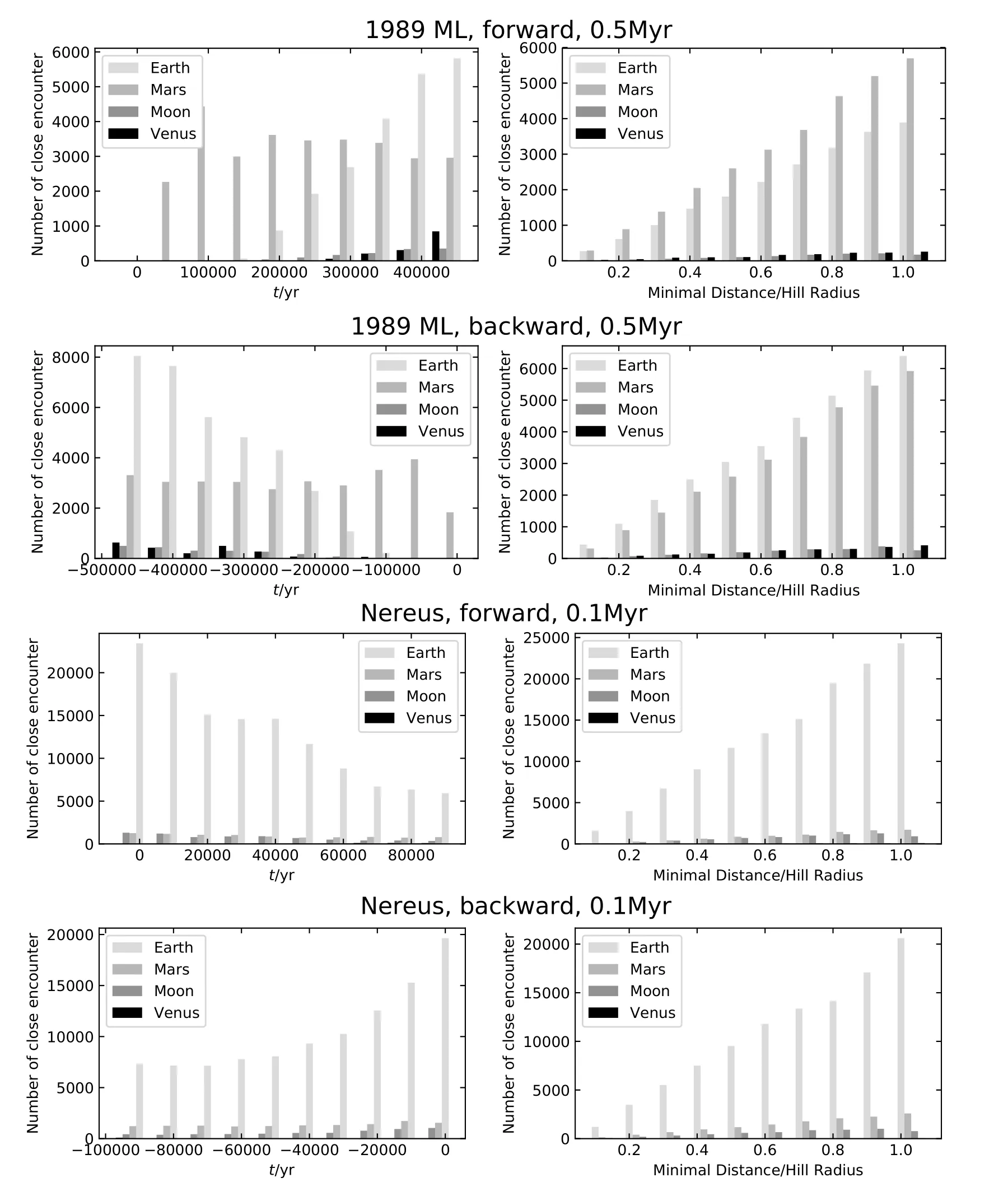
图6 两个小行星与4个类地行星的密近交汇次数统计图.左图为密近交汇时间落在等间距区间内的次数统计,右图为密近交汇时的最近距离落在若干倍行星Hill半径内的次数统计.Fig.6 The statistics of numbers of close encounters between the Asteroids and four terrestrial planets.The panels on the left show numbers of times of close encounters moment within equidistant interval,and the ones on the right show numbers of times for the nearest distances during close encounters locating in the range of several times of Hill radius of planets.

与第3.2节得出的结论相统一,由于Nereus处在地球碰撞主导的范围内,所以从一开始就与地球频繁交汇,同时交汇次数随时间呈递减关系.向前10万年内与地球的交汇次数也是随时间递减的.由此可知,Nereus目前正处在与地球最“密切”的阶段.相对而言,与月球和火星的交汇次数相当,与金星也有交汇,次数较少.同时,统计中向后10万年内

他们性格迥然，爱好有别，但对市场、生存、竞争天生敏感，绝不含糊。他们能够忍受：高强度工作、长时间压力、不确定风险。

还有3次与Vesta交汇,向前10万年内与Vesta交汇4次,与Ceres交汇2次.

表4和表5给出了两个小行星与各大行星在向后一段时间内的碰撞次数及概率.可以看出,1989 ML一直到50万年与各大行星的碰撞概率都很小;而Nereus在10万年内的碰撞均是与地球发生的,这也与图5中它在a-e相空间中的轮廓分布相一致.

表4 1989 ML在10万年及50万年内与各大行星的碰撞次数及概率统计Table 4 Number of times and probability statistics of collisions between 1989 ML and planets within 0.1 Myr and 0.5 Myr

表5 Nereus在10万年内与各大行星的碰撞次数及概率统计Table 5 Number of times and probability statistics of collisions between Nereus and planets within 0.1 Myr

3.4 共振分析

影响近地小行星的共振主要包括长期共振、Kozai共振及与类地行星的平运动共振.长期共振主要作用是激发小行星的轨道偏心率或轨道倾角,是轨道不稳定的一个因素.而Kozai共振,即近点角距被锁定在某个固定值时(低倾角时在0或180°,高倾角时在90°或270°[27],或者说,低倾角时轨道近心点一直在轨道升交点或降交点附近,而高倾角时轨道近心点一直在轨道升交点和降交点中间的两点附近),小行星在近心点或远心点时穿过黄道面(即近点角距为0或180°),而其近心点或远心点离1 au较远,所以可以很好地避开与地球的密近交汇,从而保持稳定.相类似地,平运动共振也可使小行星避开密近交汇,从而增加某个轨道的稳定时间.

图7和图8给出了1989 ML的标称轨道在向前向后演化3 Myr的过程中受到各种共振的影响.由图中看出,小行星1989 ML在所展示的时间段内与地球、火星和土星均有长期共振的作用.同时在向后的演化中,小行星的密近交汇较向前演化明显少了很多,主要归因于平运动共振,包括火星25:19、地球7:10、金星3:7和水星1:6位置.其中与地球的7:10共振发生的时间持续最长,对于稳定轨道起了主要作用.

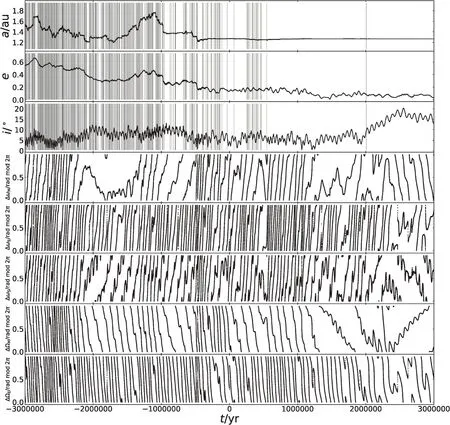
图7 1989 ML标称轨道向前向后演化3 Myr过程中半长径、偏心率、轨道倾角及与地球、火星、木星的长期共振角随时间的演化.从上到下纵坐标依次为半长径、偏心率、轨道倾角、与火星、地球、土星的ω长期共振以及与火星、地球的Ω长期共振,共振角表达式分别为∆ωM= ω−ωM、∆ωE= ω−ωE、∆ωS= ω−ωS、∆ΩM=Ω−ΩM、∆ΩE=Ω−ΩE,其中ω、ωM、ωE、ωS分别为小行星、火星、地球和土星的近点角距,Ω、ΩM、ΩE分别为小行星、火星、地球的升交点经度.图中灰色竖线表示在对应时刻发生的密近交汇,黑色竖线表示发生密近交汇时与主天体的最小距离小于0.001 au.Rad mod 2π表示对2π取模.Fig.7 The time evolution of semi-major axis,eccentricity,orbital inclination of the nominal orbit of 1989 ML and its secular resonance angles with Earth,Mars and Jupiter in the process of 3 Myr forward and backward.From top to bottom Y-axes are semi-major axis,eccentricity,orbital inclination,ω secular resonance with Mars,Earth,Saturn,as well as Ω secular resonance with Mars and Earth,the resonant arguments are ∆ωM= ω−ωM,∆ωE= ω−ωE,∆ωS= ω−ωS,∆ΩM=Ω−ΩM,∆ΩE=Ω−ΩE respectively.Here,ω,ωM,ωE,ωS are the arguments of periastron of asteroid,Mars,Earth and Saturn,Ω,ΩM,ΩE are longitudes of ascending node of asteroid,Mars and Earth,respectively.In the figure,the grey vertical line indicates close encounters occurring at the corresponding time,and the black vertical line indicates that the minimum distance from the main body during the close encounter is less than 0.001 au.Rad mod 2π denotes modulo 2π.

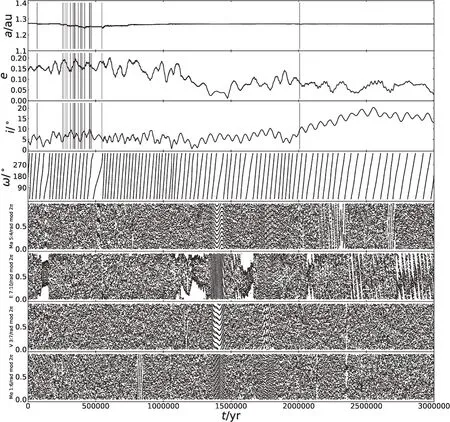
图8 1989 ML标称轨道向后演化3 Myr过程中半长径、偏心率、轨道倾角、近点角距及与类地行星的4个平运动共振角随时间的演化,从上到下依次为火星5:4、地球7:10、金星3:7、水星1:6.图中灰色竖线表示在对应时刻发生的密近交汇,黑色竖线表示发生的密近交汇的最小距离小于主天体的0.001 au.Fig.8 The evolution of semi-major axis,eccentricity,orbital inclination,argument of pericentre of the nominal orbit of 1989 ML and its Mean Motion Resonance critic angles with the terrestrial planets versus time in the process of 3 Myr forward.From top to bottom:5:4 with Mars,7:10 with Earth,3:7 with Venus,and 1:6 with Mercury.In the figure,the grey vertical line indicates close encounters occurring at the corresponding time,and the black vertical line indicates that the minimum distance from the main body during the close encounter is less than 0.001 au.

Nereus的标称轨道向前向后演化3 Myr的过程中,其受到的各种共振作用如图9和图10所示.Nereus的演化中发生密近交汇的频率较大,但有两个时间段很稳定,没有任何的密近交汇,分别是0.7–1.2 Myr和1.5–2.8 Myr.而这两个时间段分别对应地球的11:14平运动共振和Kozai共振(图10中从上到下第6、4图),说明了这两种共振对小天体的保护作用.值得注意的是,文献[18]中选取的Nereus的5个克隆粒子的演化过程中也出现了以上两个共振的作用.同时小天体还受到地球、火星和土星较明显的长期共振作用.

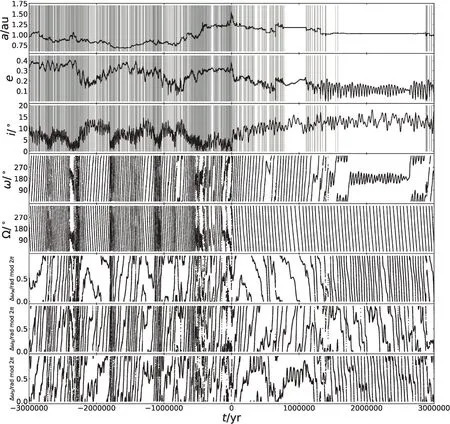
图9 Nereus标称轨道向前向后演化3 Myr过程中半长径、偏心率、轨道倾角、近点角距、升交点经度及与火星、地球、土星的ω长期共振角(按从上到下的顺序∆ωM= ω−ωM,∆ωE= ω−ωE,∆ωS= ω−ωS,其中ω、ωM、ωE、ωS分别为小行星、火星、地球和土星的近点角距)随时间的演化.图中灰色竖线表示在对应时刻发生的密近交汇,黑色竖线表示发生的密近交汇的最小距离小于主天体的0.001 au.Fig.9 The evolution of semi-major axis,eccentricity,orbital inclination,argument of pericentre,longitude of ascending node of the nominal orbit of Nereus,as well as its secular resonance angles with Mars,Earth and Jupiter versus time in the process of 3 Myr simulation forward and backward (from top to bottom are ∆ωM= ω−ωM,∆ωE= ω−ωE,∆ωS= ω−ωS.Here,ω,ωM,ωE,ωS are the arguments of periastron of asteroid,Mars,Earth and Saturn.).In the figure,the grey vertical line indicates close encounters occurring at the corresponding time,and the black vertical line indicates that the minimum distance from the main body during close encounter is less than 0.001 au.

图10 Nereus标称轨道向后演化3 Myr过程中半长径、偏心率、轨道倾角、近点角距及与类地行星的4个共振角(从上到下依次为火星3:2、地球11:14、地球7:10、金星1:2)随时间的演化.图中灰色竖线表示在对应时刻发生的密近交汇,黑色竖线表示发生的密近交汇的最小距离小于主天体的0.001 au.Fig.10 The evolution of nominal orbit of Nereus with time for backward within 3 Myr,including semi-major axis,eccentricity,orbital inclination,argument of pericentre and four resonance angles with the terrestrial planets (from top to bottom:Mars 3:2,Earth 11:14,Earth 7:10,Venus 1:2).In the figure,the grey vertical line indicates close encounters occurring at the corresponding time,and the black vertical line indicates that the minimum distance from the main body during the close encounter is less than 0.001 au.

4 结论

近地小行星(10302) 1989 ML与(4660) Nereus是下一代小行星探测项目的重要候选体.本文从动力学方面研究了这两个小行星的轨道特征及演化可能性.首先,结合N体运动方程、轨道距离变分方程和MEGNO指数对应的两个方程,通过积分给出了最大Lyapunov指数与MEGNO指数,从而计算出1989 ML和Nereus的Lyapunov时间分别为251 yr和18 yr.其次,通过对1000个克隆粒子的统计,给出了小行星在10万年内各轨道根数可能的运动范围,显示了小行星在半长径-偏心率相空间中的出现次数分布图,同时对50万年内1989 ML小行星(10万年内Nereus小行星)与大行星的密近交汇及碰撞次数进行了统计分析.最后,针对标称轨道,分析了前后3 Myr内不同时间段所受的各种共振及具体影响.

由于本文中所用力模型较粗糙,并没有考虑譬如相对论效应、非球形引力及太阳光压、Yarkovsky效应等非引力效应,所考虑的引力效应中仅包含4个最大的小行星,没有考虑更多小行星的影响,所以只能基于统计做定性分析,并未涉及定量的短期轨道预测.基于历表的高精度短期轨道计算及小行星所需力模型的讨论分析,应是下一步工作的方向之一.

附录

本文利用N体运动方程、轨道距离变分方程及MEGNO指数的两个方程来计算MLE及MEGNO指数.N体运动方程表达式如下:

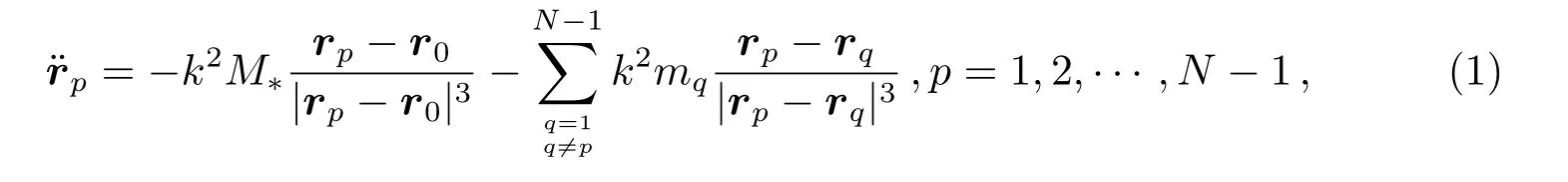
或者将右面两项合并,也可写作

其中M∗、mq分别表示中心天体(此处为太阳)和第q个天体的质量,r0、rq分别为中心天体和第q个天体相对于系统质心的位矢.为简便起见,以下推导均用(2)式.

该表达式表示成一阶微分方程组的形式如下:

此方程组也可表示为以下向量形式:

在此基础上利用以下公式来计算最大Lyapunov指数L、MEGNO指数Y及平均MEGNO指数〈Y〉,

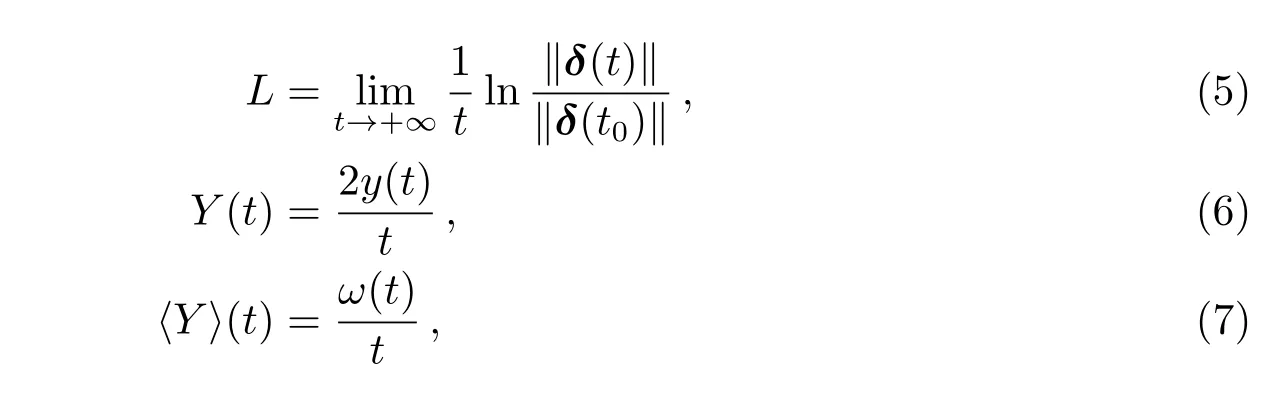
‖·‖表示对其中向量求范数,计算时可用向量的模这一特殊范数代替.式中参数由以下微分方程组来计算:

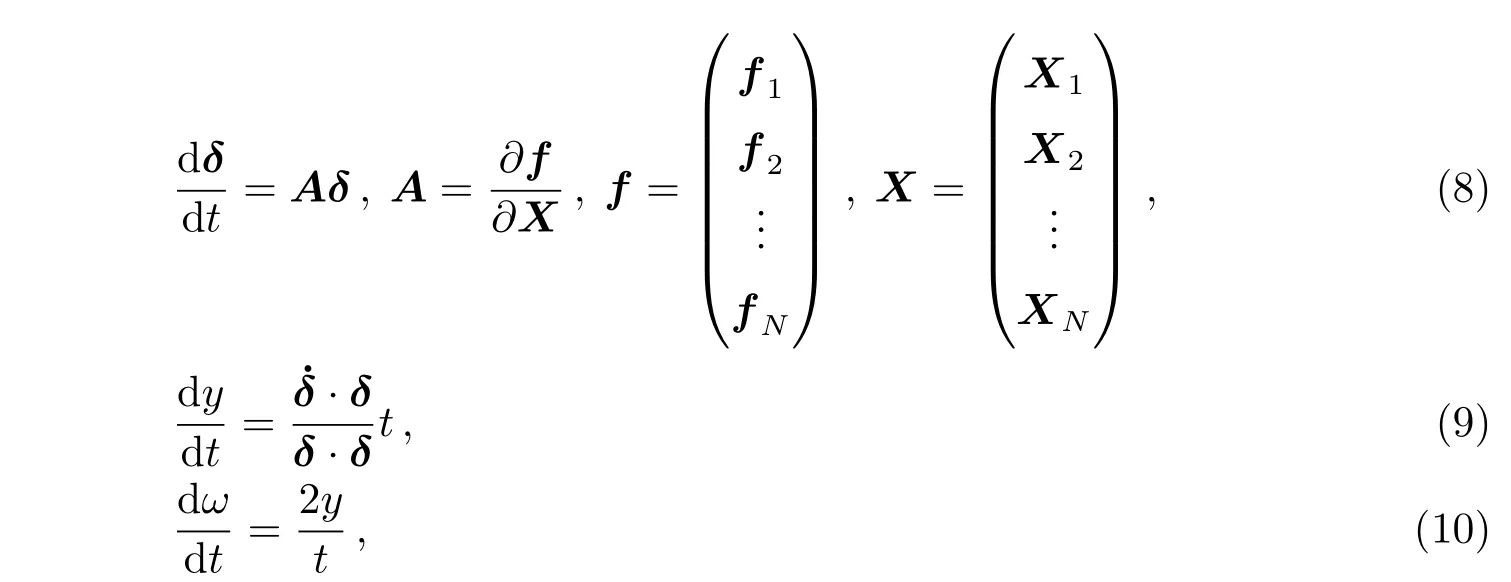
其中δ为6N维向量,表示相邻轨道间距或轨道发散指标,A为函数向量f对变量向量X的6N×6N维雅克比矩阵,具体表达式如下:

其中

将A的表达式代入关于δ的微分方程组((8)式),可得

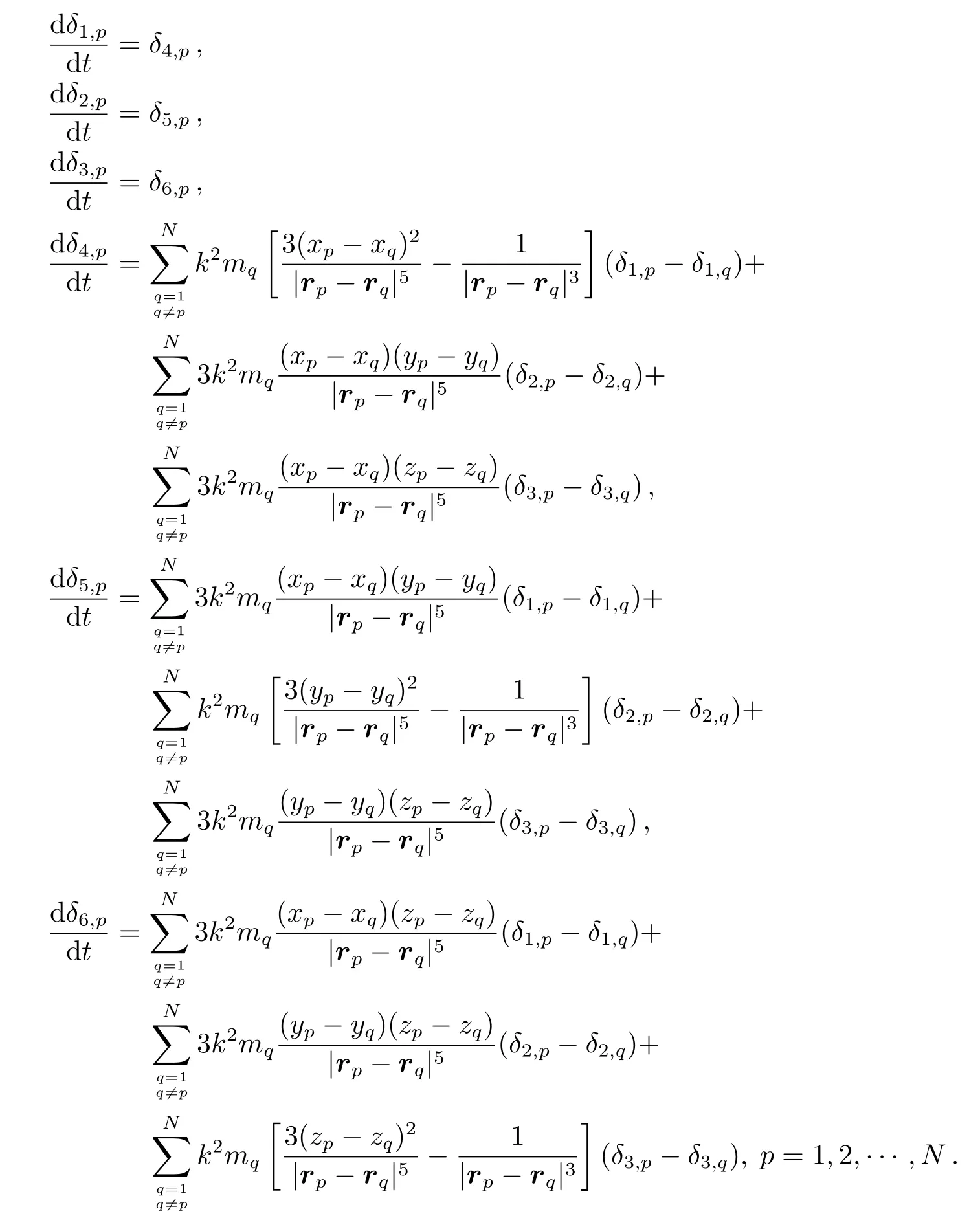
此处6N个微分方程组与(2)式中的6N个微分方程组结合,计算103–104倍的系统特征周期(可看作系统中最外面大天体的轨道周期),即可得到可靠的MEGNO指数[23].