基于三维X-CT图像的结皮土壤孔隙结构特征与渗透率

许智隼，胡五龙,2※

（1.武汉理工大学理学院，武汉430070；2.武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心，武汉430070）

0 引 言

在干旱半干旱地区，表层土壤会在外部物理夯实或内部微生物作用下形成一种低入渗率、高抗剪强度的土壤结皮[1]，即土壤物理结皮或土壤生物结皮。根据不同的形成机理和发育过程，土壤物理结皮可以分为由雨水等外力打击而形成的结构性结皮和由径流冲刷引起的沉积性结皮[2-3]。土壤结皮中的微生物可以有效地富集并吸收土壤中的重金属，对治理环境污染具有一定的积极意义[4]。同时，土壤结皮也会显著降低土壤水分向地下入渗，增加地表径流[5-6]，造成水土流失[7]，进而可能引发一系列严重的生态环境灾害。目前国内外对土壤结皮的研究主要聚焦于其成因和功能方面，而对土壤结皮的微观孔隙结构及其对水力特性的影响研究较少[8-9]。

土壤孔隙是气体、水和营养物质输运的通道，同时也是土壤微生物的栖息地[10-12]。因此，土壤孔隙结构在很大程度上影响或决定了土壤肥力，对生态环境、地下水系统及大气循环有着重要影响。同时，土壤中的所有物理过程及生化反应都发生在孔隙中，而目前的试验技术手段很难对孔隙中的这些过程和反应进行准确观测，因此基于真实土样三维孔隙结构从孔隙尺度模拟土壤中水的输运，有助于精确描述土壤中水的输运过程和相关机制。

土壤孔隙结构的传统研究方法有切片法[13]、压汞法[14]和氮吸附法[15]等，这些方法不仅会破坏土壤原有的孔隙结构，而且难以重构土壤内部的三维孔隙结构。显微成像技术，尤其是 X射线断层扫描成像技术（X-ray Computed Tomography，X-CT）的快速发展，使人们能够获取真实土壤的三维孔隙结构并对其进行分析。与传统的研究方法相比，X-CT是一种不损害土壤孔隙结构的三维成像技术，其分辨像素尺寸甚至可以小于1μm，已被广泛应用于油气开采、地下水盐运移、污染物扩散等与土壤相关的工程实践与科学研究中[16]。Katuwal等[17]和Hu等[18]利用X-CT研究了土壤孔隙的几何结构与其水气特性间的关系。程亚南等[19]利用CT扫描技术重构了土壤的三维孔隙结构，并建立了孔隙网络模型来预测孔隙结构的水力学性质。杨永辉等[20]利用X-CT研究了不同土壤结构改良措施下的土壤孔隙特征，为合理地应用耕种方式提供了科学依据。利用 X-CT技术对土壤结皮进行研究，一方面可以在真实结皮土样三维孔隙结构基础上分析其孔隙特征及分布规律，另一方面可以基于真实土样结构图像孔隙尺度模拟结皮土样中水的渗透过程。然而，迄今为止，尚未有利用X-CT研究土壤结皮三维孔隙结构及其分层特征的报道，对土壤结皮的结构特征和渗流特点的孔隙尺度认识也尚不明确。格子玻尔兹曼方法（Lattice Boltzmann Method，LBM）是近三十年发展起来的流体数值计算方法，它采用粒子分布函数直接模拟计算域中流体粒子的运动，具有成像清晰、算法简单、易于并行和适应复杂几何边界条件的特点，因而非常适合用来模拟多孔介质中传热和传质过程[21]。结合X-CT技术，利用LBM可以更逼真地模拟孔隙介质中流体运动[22]，为探究多孔介质的渗流机理提供了一种高效精确的方法[23]。

本文拟对3个有表层结皮的土样孔隙结构及渗透率进行分层分析，先采用X-CT和图像处理技术获取三个土样的三维孔隙结构图像，然后将这些图像沿深度方向分层，分析各深度层内土样的孔隙结构特征。最后结合格子玻尔兹曼方法计算各深度层的渗透率，探讨土样的孔隙特征对渗透率的影响，以期为干旱区半干旱区合理管理利用地下水资源和保护生态环境提供参考。

1 材料与方法

1.1 三维X-CT图像获取

本文对 3个表层有结皮的土样进行孔隙结构和渗透率分析。原土样采自英国贝德福德郡一处田地，提取地表10 cm厚土层，在实验室烘干捣碎去除植物根茎和粗颗粒后做成半径和高均为10 cm的土样，三个土样均为粉黏土。通过喷淋方式模拟降雨，给定三个土样不同的降雨量。然后将土样至于置于实验室环境试验箱中模拟半干旱地区蒸发环境条件，待表层出现明显结皮后，用环刀从土样上部重新提取小柱状土样，将提取的小柱状土样通过Phoenix Nanotom扫描系统获得一系列的X射线投影图像，然后使用扫描系统的配套软件 Phoenix datos|x2和重建算法将投影图片重构为三维X-CT图像，并导出三维图像的二维连续切片图。X-CT图像的显示分辨率与扫描视野相关，本文为了显示土样的全貌，采用了较低显示分辨率的扫描方式，切片图像的分辨率为40μm。扫描的柱状土样周边孔隙结构会受取样时环刀影响发生改变，为此截取三个土样中心区域的扫描图像用于后文的分析和计算。由于原始的切片图像是灰度图，本文仅关注土样的孔隙特征，因此利用开源软件 ImageJ将这些连续切片图像进行二值化处理，方便进一步的可视化和计算[24]。最终的三维图像如图1所示，三个土样的 尺 寸 分 别 为 937×937×1000 、 912×912×1000 和933×933×1000体素（voxel），其中浅色部分为固相，深色部分为孔隙。为了讨论土样孔隙结构沿深度方向（图1中z方向）的变化规律，由上表面开始每100 voxel（即4 mm）取一土层，并依次编号为土层1～9。

1.2 结构特征分析方法

在经过二值化处理后，土样的结构信息被存储在一个三维数组中，数组中的每个元素都为0或1，分别表示土样的孔隙相和固相，因此土壤孔隙率可由数组中“0”元素的数量简单得到。

式中φ表示孔隙率；N0表示数组中“0”元素的数量；N0&1表示数组中“0”元素和“1”元素的总数。

孔隙变异度是指当前土层与其相邻土层的孔隙率差异程度[12]，可用下式来计算：

式中E表示孔隙变异度，%；φu和φb分别表示当前土层和下层土的孔隙率。

在计算孔隙直径时，采用形态模型方法[25]，即以不同直径的球填充孔隙空间，对于每个孔隙体素，取包含该孔隙体素的最大球直径为其对应的孔隙直径。由于三维图像是由一个个体素组成的三维矩阵，而体素为一个边长为 1的小立方体，因此孔隙之间可以通过立方体的角点、棱线和面来连接。由于不连通孔隙和微小孔隙（孔隙直径小于分辨率）中的水分几乎不发生迁移，故在本文研究中忽略这部分孔隙体积，并假设流体仅在连通孔隙中传输，仅当两个孔隙体素以面连接才视为连通，孔隙连通率可由下式给出：

式中Rp为孔隙连通率，%；φ和φc分别为总孔隙率和连通孔隙率。

土壤孔隙复杂度可由分形维数[13]来进行定量评价。在二维情况下，规则图形的周长-面积满足以下关系：

式中C为二维图形的周长，mm；A为二维图形的面积，mm2。

对于不规则图形，可以使用分形周长[26]来代替上式中的实际周长。分形周长和分形面积之间满足

式中ε表示测量尺度，C(ε)和A(ε)表示在该尺度下测得的周长和面积。因此，分形维数D可以通过采集不同测量尺度ε的C和A，然后绘制lgC-lgA曲线来获得。由于实际中往往只应用了一个尺度来测量图形的相关信息，缺少其他尺度下的C和A值，因此常用下式来近似地求取D：

上述求取分形维数D的方法称为“小岛法”[12,27]，其讨论的是复杂二维图形的周长-面积关系，本文研究土壤三维孔隙结构，需在上式基础上进行改进。假设复杂三维图形的表面积S（mm2）和体积V（mm3）满足

那么，三维图形的分形维数D可以近似地表示为

式中分形维数D表征孔隙结构复杂度（后文简称“孔隙复杂度”）；S表示三维图形的分形表面积，而V表示其分形体积，二者的单位需要相互对应，在本文中分别为mm2和 mm3。

从式（8）来看，孔隙复杂度D与比表面积具有相似的描述能力，即相同表面积下，体积越大的孔隙，D值越小，其孔隙结构越简单。

1.3 渗透率计算

基于 Bhatnagar-Gross-Krook（BGK）算子的格子Boltzmann基本方程[28]如下式所示：

式中i表示离散速度方向；ei为无量纲离散速度；fi(x,t)和fieq(x,t)分别为t时刻x处的分布函数和平衡态分布函数；c=Δx/Δt表示离散格子速度，Δx和Δt分别为格子空间步长和格子时间步长，在 LB模拟中一般取为 1；τ为无量纲松弛时间。

平衡态分布函数fieq(r,t)由Maxwell-Boltzmann分布的Hermite展开[29]来确定

式中cs=c/代表无量纲格子声速；ρ和u分别表示x处流体粒子的宏观密度ρ（g/cm3）和宏观速度u（mm/s）；wi是权重系数，由离散速度模型所确定。

本文采用 D3Q19模型[30]，即将式（9）和式（10）在三维速度空间按照 19个方向进行分解，格子模型如图2所示。

那么，i方向上的离散速度矢量ei即图2中的各空间矢量，如e0=（0, 0, 0），e1=（1, 0, 0），e7=（1, 1, 0），以此类推。与之相对应的权重系数分别取w0=1/3，w1-6=1/18，w7-18=1/36。

流体的宏观密度和宏观速度别由分布函数的一阶矩和二阶矩给出

式（11）和（12）得到的流体密度和速度为格子单位，可换算为实际物理单位。

流体的运动黏度υ（mm2/s）为

作用在流体粒子上的压力P0（Pa）由状态方程[21]给出

在模拟过程中，假设水是不可压缩的，其密度ρ=1.0 g/cm3。在LB M模拟中，流体的压力与密度成正比，在水密度恒定的条件下流场中的压力处处相等，与流体力学中由压力梯度来驱动流体流动的客观事实相悖。为模拟土壤中水渗透过程，本文将土样顶部的流体密度设置为ρ1=1.0+0.000 2Lzg/cm3，Lz是图像的高度，土样的底部则设置为ρ2=1.0 g/cm3，四周为周期性边界条件。压力边界条件的具体格式参考Zou等[31]的非平衡态外推边界。

当土样中的体积流量（m3/s）在前后两个时间步间相差小于10-6，则认为渗流达到稳定状态。此时，可由达西定律求出渗透率[32]

式中q为体积平均流速，mm/s；k为渗透率，mm2；∇P为压力梯度，Pa/mm。

在z方向（竖直方向）上施加压力梯度时，z方向上的渗透率分量kzz表示为[23]

式中的平均流速qz（mm/s）由下式给出：

式中∑ui,z表示图像中各个流体粒子在z方向上的速度分量之和，mm/s；N=NxNyNz，为土样图像的体素（voxel）个数，Nx、Ny和Nz分别为土样图像x、y、z方向的体素数。

模拟过程中，所有物理量包括长度、密度等均直接采用格子单位，计算结果最后转换成实际的物理单位，1 lu =1 voxel（lu为格子单位）。

2 结果与分析

2.1 孔隙结构特征分析

2.1.1 孔隙率与孔隙连通性分析

表1显示了3个结皮土样的基本信息，从统计结果来看，尽管三个土样的孔隙率具有较大的差异，但其平均孔隙直径均在0.2 mm左右。土样1具有较好的整体连通性，孔隙连通率（连通孔隙体积与总孔隙体积之比）达91.26%，而土样2和3的整体连通性则较差。

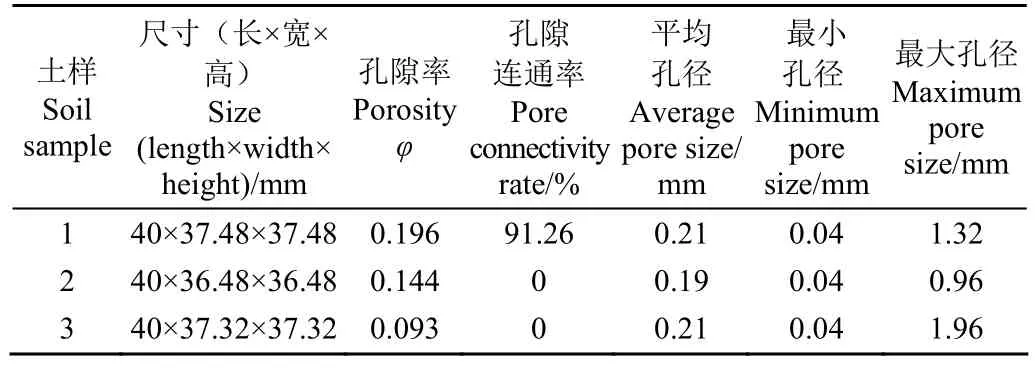
表1 土样的基本几何参数Table 1 Basic geometric parameters of soil crusts

图3a为三个土样各水平切片上的孔隙率沿深度变化规律，从图中可以看出，土样表层具有较大的孔隙率，但与其紧邻的下层土的孔隙率陡降，在1～2 mm深度达到一个极小值。从图3b的孔隙变异情况来看，土样上表面几层切片在孔隙率上具有较大的差异，其变异系数E＞5%。这种差异可能会导致其渗透能力表现出截然不同的特点。

与图3a相对应，各土样的1～9土层的最大深度分别为h=4～36 mm（每层4 mm）。图4a显示了三个土样每个土层的孔隙率，从图中可以看出，当土层厚度取为4 mm时，三个土样的连通孔隙率均表现出两端孔隙率小、中间孔隙率大的整体变化趋势。图4a中每个土样虚实线的相对位置关系显示了土层孔隙连通性的差异。从计算结果来看，三个土样各土层的孔隙连通率最大值分别为99.21%、94.64%和57.35%，处于土样中部，而最小值分别为45.99%、27.30%，和11.74%，处于土样的两端，各土样均表现出两端连通性较差而中间连通性较好的整体趋势。图4b显示了三个土样各土层总孔隙率与孔隙连通率间的关系，对二者进行相关性分析，显示相关系数r=0.97，P＜0.01，表明总孔隙率与孔隙连通率存在极显著的相关性。从图中的趋势来看，土壤孔隙率越高，其孔隙连通性越好。

2.1.2 孔径分布分析

三个土样的孔径d分布如图5所示，均近似服从泊松分布。尽管三个土样孔径分布区间各不同，但直径d小于0.4 mm的孔隙均占据主要部分，分别占比94.02%，93.54%和 94.61%。而孔径分布云图显示，直径大于0.4 mm的孔隙主要分布在土样的表层部分。

图6显示了各个土层的平均孔隙直径，从图中可以看出表层土（h≤4 mm）的平均孔径与相邻土层表现出较大的差异，其余各层间的变化则较为平缓，总体上各土层的平均孔径随着深度的增加而减小，三个土样各土层的平均孔径分别由表层土（h≤4 mm）的0.43、0.37和0.50 mm降低至深层土（h≥32 mm）的 0.15、0.14和0.14 mm。这种变化规律一方面是由于表层土直接裸露在空气中，与外界的物质交换频繁，且受雨水侵蚀、动植物活动的影响较大；另一方面，土壤水分携沙下渗时，细土粒在下部淤积，从而阻塞孔隙，使得下土层的孔径变小。

2.1.3 孔隙复杂度分析

由于土壤中的水主要在连通孔隙中流动，因此忽略孔径小于图像分辨率的微孔，在此仅讨论土样中连通孔隙的复杂程度。表2列出了三个土样各土层中连通孔隙的表面积S与体积V值，在此基础上根据式（7）计算各土层的孔隙复杂度D。

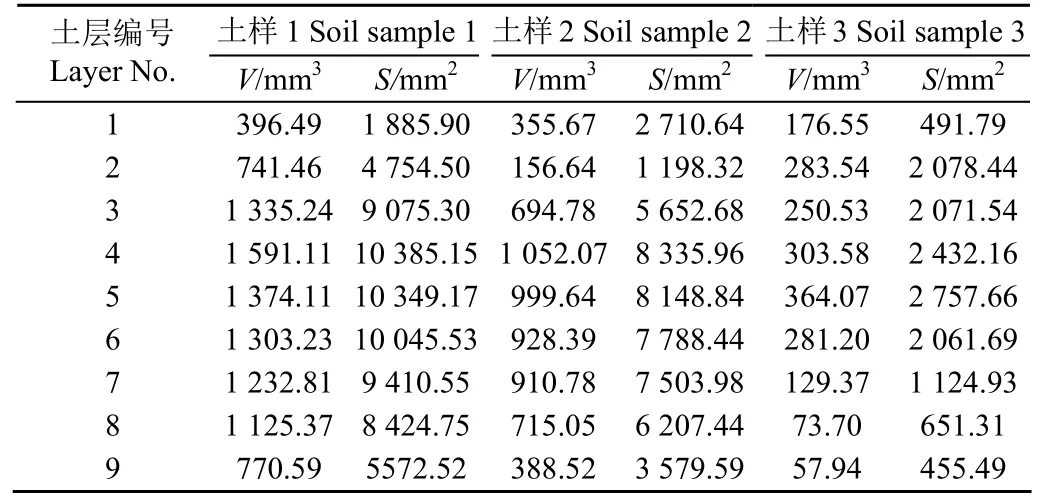
表2 各土层连通孔隙的表面积（S）与体积（V）Table 2 Surface area(S) and volume(V) of connected pores of each soil layer

最终的孔隙复杂度计算结果如图7所示。从图7 a可以看出，三个土样间的孔隙复杂度有着明显的不同，土样1的D值最小，而土样3的最大。从式（8）及孔隙复杂度的定义来看，孔隙复杂度与土壤孔隙的体积密切相关。图7 b显示了孔隙复杂度D与连通孔隙率间的关系，从总体上的趋势来看孔隙率越高的土层，具有更小的D值，其孔隙结构更加简单。对D和φ进行Spearman相关性分析，二者的相关系数r=-0.90，P＜0.01，这表明孔隙复杂度与连通孔隙率呈极显著负相关关系。图7 b中，土层1-1和3-1偏离总体趋势，这是由于土样1和土样2表层土壤因外部作用产生了大面积的凹陷，形成了不平整的表面，这些表面凹陷在算法中被当成了孔隙统计进来，从而使得表层土壤的孔隙复杂度大幅降低。

2.2 渗透率分析

2.2.1 孔隙结构参数对渗透率的影响

通过Boltzmann方法和1.3节的边界处理方式模拟了三个土样各土层的渗流过程，并计算其渗透率，当前后两个时间步的渗透率值相差小于10-6，则认为迭代收敛，渗流达到稳定状态[23]。最终的渗透率计算结果如图8所示，从其沿深度变化的规律来看，各土层的局部渗透率沿深度方向先增加后减小，这与其连通孔隙率沿深度变化的规律基本一致。土层3-1渗透率kzz高达1093μm2，而土样3其他土层的最大局部渗透率仅为23.522μm2，二者之间存在数量级的差异。分析土层3-1的孔隙发现在该土层存在一个上下通透的穿孔，如图9所示，图中白色透明的部分即为该土样穿孔，该穿孔的存在是其渗透能力显著强于其他土层的主要原因。

去掉土层3-1后，发现三份土样中含结皮的表层具有较小的渗透率值，分别为7.472、0.006和6.960μm2，这表明结皮对土壤水的渗流有较强的阻滞作用。图10显示了土样各结构参数与渗透率间的关系，从图中结果来看，渗透率随孔隙率和孔隙连通性的提高而增大，随孔隙复杂度D的提高而降低。渗透率与平均孔隙直径间则没有明显的单调变化趋势，从图10 c来看，平均孔径在0.16～0.20 mm间的土层具有较高的渗透率，这是由于这些土层均具有较高的孔隙连通率。

对这些结构参数与渗透率进行 Spearman相关性分析，结果如图10所示。连通孔隙率与渗透率间极显著正相关（相关系数为正，且P＜0.01），孔隙复杂度与渗透率极显著负相关（相关系数为负，且P＜0.01），而平均孔径和比表面积对渗透率大小的描述能力则较差（P＞0.05）。

应用SPSS对图10中的散点进行曲线估计以选择最优的回归模型，其结果如表3所示。在曲线估计时，选择了SPSS中所有可选的回归模型。从估计的结果来看，孔隙连通率φe和孔隙复杂度D能够一定程度上对渗透率的数值结果做出预测，其决定系数较高且回归分析具有显著的统计学意义（P＜0.05），而应用比表面积Ss和平均孔径dave的回归模型的误差则较大。

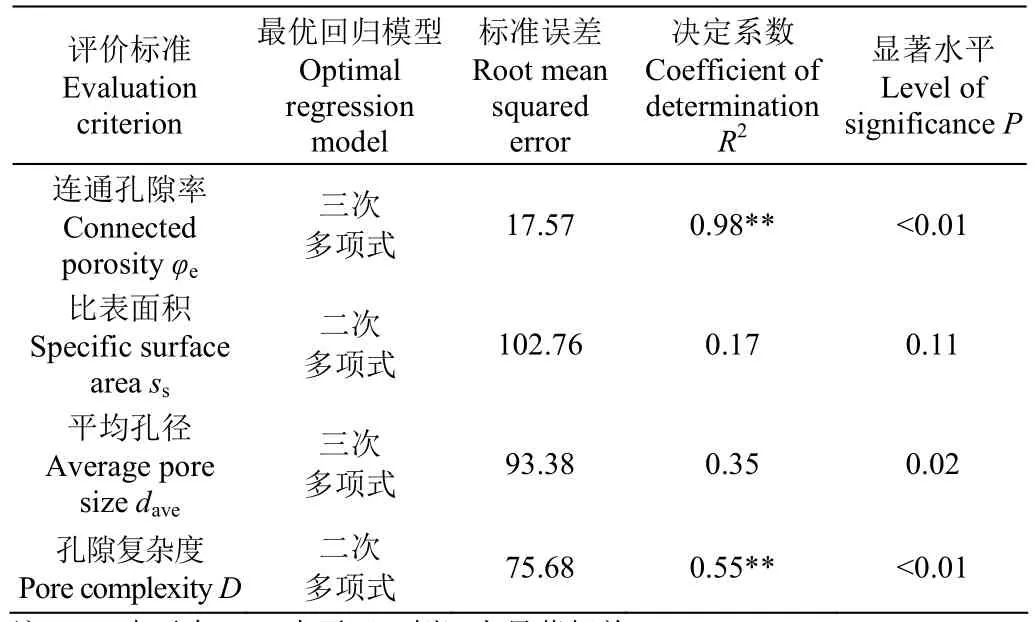
表3 结构参数与渗透率间的最优回归模型估计Table 3 Optimal regression model estimation between structural parameters and permeability

2.2.2 渗透率预测模型与改进

从前文的结构特征分析来看，孔隙率更高的土层具有更高的孔隙连通率和更小的孔隙复杂度，其相关性分析的P值均小于0.05。这些相关性分析表明，土壤孔隙率能够在很大程度上描述土壤孔隙的结构特征，并能通过孔隙率来预测土壤的渗透率。在已有的研究中，大多数的渗透率预测模型都是将孔隙率作为输入参数。早在20世纪，Kozeny就将渗透率与孔隙率和孔隙形状联系起来，建立了水力传导理论的基础[33]，而后Carman在进一步的工作中提出了广为人知的Kozeny-Carman（K-C）方程[34-35]。然而原始K-C方程中有许多难以获取的结构参数，因此一些基于K-C方程的简化模型在实际应用中更为广泛[36]。利用两种常用渗透率预测模型拟合LBM数值计算结果，如图11所示，其中简化K-C方程的拟合参数C=（1.302±0.036）×104μm2，拟合程度R2=0.97；而Tomadakis的预测模型中的拟合参数C=（4.603±0.176）×104μm2，相应的拟合程度R2=0.94。从拟合结果来看，简化K-C方程具有更高的精度，即k-φ之间满足

应用比表面积SS的原始K-C方程如下所示：

为使预测模型能够较为准确地描述孔隙复杂度D对渗透率的影响作用，并提升模型的预测精度，这里将D引入简化K-C方程。由于D与k负相关，即k随D的增加而减少。而从D的定义来看，D与比表面积SS具有相似的描述能力，且D与k的相关程度要显著高于D与SS的相关程度。因此，可用D来替换式（20）中的比表面积SS，即

改进模型拟合LBM数值计算结果如图12（b）所示，其中拟合参数C=(2.480±0.068)×104μm2，R2=0.98，RMSE=18.31μm2，较改进之前的模型（R2=0.96，RMSE=25.06μm2）具有更高的预测精度。从上式来看，k随孔隙率φ的增加而增加，随孔隙复杂度D的增加而减小，与图10表现出的趋势基本一致。

3 结 论

本文采用X-CT成像技术和图像分析方法，获取了三个表层有结皮的土样，分析了其孔隙结构特征及相关规律，结合单相渗流LBM（Lattice Boltzmann Method，格子玻尔兹曼方法）计算了各土样不同深度土层的局部渗透率，在此基础上对结构特征参数与渗透率的相关性进行了分析，并提出了根据土壤孔隙率和复杂度计算渗透率的分形维数模型，得到了以下结论：

1）结构分析表明，土样表层和底层的孔隙率及其孔隙连通性均小于中间土层，三个土样各土层的孔隙连通率最大分别为99.21%、94.64%和57.35%，处于土样中部，而最小值分别为45.99%，27.30%和11.74%，处于土样的两端；顶层土孔隙结构较相邻土层具有较大的差异，变异程度更大，其变异系数E＞5%。各土层的平均孔隙直径随着深度的增加而减小，分别由0.43、0.37和0.50 mm降低至0.15、0.14和0.14 mm；孔隙率更高的土层具有更好的孔隙连通性和更低的孔隙复杂度，相关系数达0.97。

2）渗透率计算结果显示，土样表层具有较低的局部渗透率，分别为7.472、0.006和6.960μm2，表明结皮对土壤渗流具有阻滞作用；孔隙率越高、孔隙连通性越好、孔隙复杂度越低的土层渗透能力越强。

3）基于LBM数值模拟的结果，将原始K-C方程中的比表面积替换为孔隙复杂度D，改进后的模型对土壤渗透率具有更高预测精度，其决定系数R2由0.96提升至0.98，而均方根误差RMSE则由25.06降低至18.31μm2。