基于GeoGebra的高中数学函数教学研究

胡静

摘 要：随着普通高中新课程改革不断深化，运用信息化手段来辅助教学引起了人们越来越高的重视。选择一种科学、高效的教学模式方法，更加有助于学生数学学科素养的有效提升。本文主要以幂函数课后探究活动：探究函数图像和性质以及对勾函数的教学为例，探讨了如何利用数学软件GeoGebra（GGB）开展高效的高中函数教学活动。

关键词：GeoGebra（GGB）;幂函数;函数;对勾函数;高中函数教学

1.引言

GeoGebra（GGB）是一个免费的数学教育软件，它由美国亚特兰大学的数学教授Markus Hohenwarter设计，目前得到了国际上教育工作者们的广泛使用。GGB界面简洁明了，使用方便，易于上手，功能强大，在数学中代数、几何、概率统计和微积分等多个方面都有涉及，基于GGB软件在数学教学中的优势，本文通过函数图像和性质以及一般对勾函数的教学实践案例，对其在高中函数教学中的使用展开了探讨。

2. GGB在幂函数教学中的实践

2.1 探究函数的图像和性质

人教A版普通高中教科书《数学》（必修第一册）2019年新教材（下面简称“教材”）中第三章第三节幂函数的“探究与发现“内容为“探究函数的图像和性质”。数学探究活动的开展对加深学生对数学知识的深层次理解，激发学习数学的兴趣是十分必要的。借助数学软件来辅助作图、分析对提高学生的兴趣，深化理解，拓宽思维，是关键的一步。

和分别是正比例函数和反比例函数，又都是幂函数，二者相加得到新的函数。参考教材中给出的7个问题，教师请学生思考可以从哪些方面探究这一函数（定义域、值域、单调性、奇偶性等）？在现有知识的基础上按照怎样的路径去研究？学生独立思考后小组进行讨论，教师再对于讨论的结果进行总结。对于函数的性质，主要有以下研究方法：

（5）描点，画出函数的图像，观察图像，归纳性质。

教师需注意的是，学生这时往往对于基本不等式的应用不够熟练，因此对于方法（3）中值域的研究可先给出结论，学生加以证明即可。这在教材中问题4也有体现。

此处函数图像的绘制对于学生是一个难点，这时有必要利用方法（4）对函数渐近线进行研究，但由于学生对于函数渐近线和极限的概念缺乏认识，教师此处应做必要的说明，结合函数区间上的连续性和值域画出其图像。

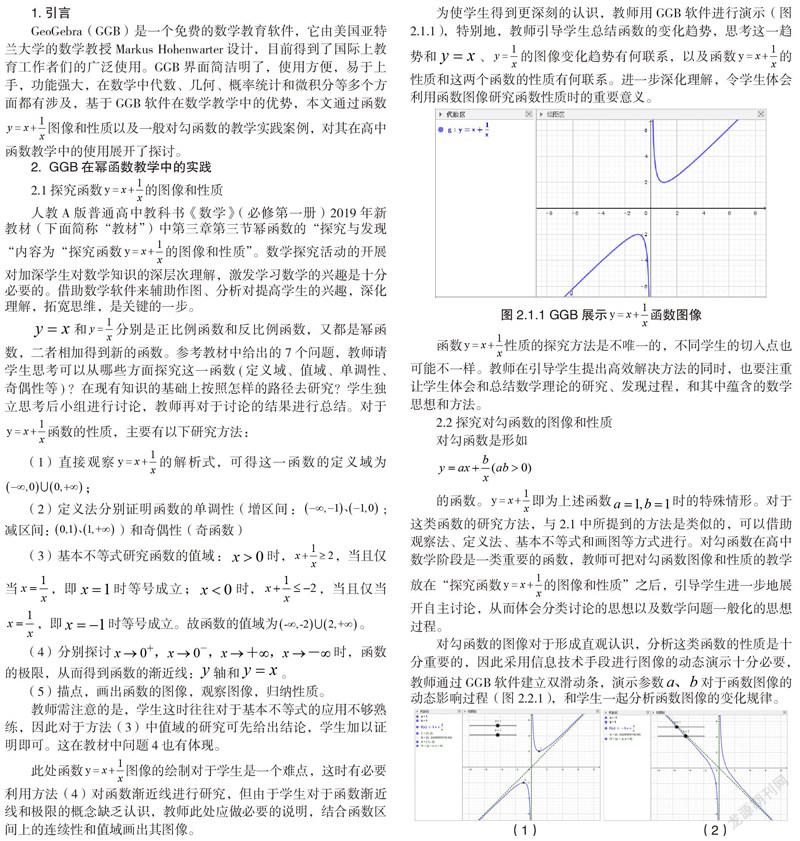
为使学生得到更深刻的认识，教师用GGB软件進行演示（图2.1.1），特别地，教师引导学生总结函数的变化趋势，思考这一趋势和、的图像变化趋势有何联系，以及函数的性质和这两个函数的性质有何联系。进一步深化理解，令学生体会利用函数图像研究函数性质时的重要意义。

函数性质的探究方法是不唯一的，不同学生的切入点也可能不一样。教师在引导学生提出高效解决方法的同时，也要注重让学生体会和总结数学理论的研究、发现过程，和其中蕴含的数学思想和方法。

2.2探究对勾函数的图像和性质

对勾函数是形如

的函数。即为上述函数时的特殊情形。对于这类函数的研究方法，与2.1中所提到的方法是类似的，可以借助观察法、定义法、基本不等式和画图等方式进行。对勾函数在高中数学阶段是一类重要的函数，教师可把对勾函数图像和性质的教学放在“探究函数的图像和性质”之后，引导学生进一步地展开自主讨论，从而体会分类讨论的思想以及数学问题一般化的思想过程。

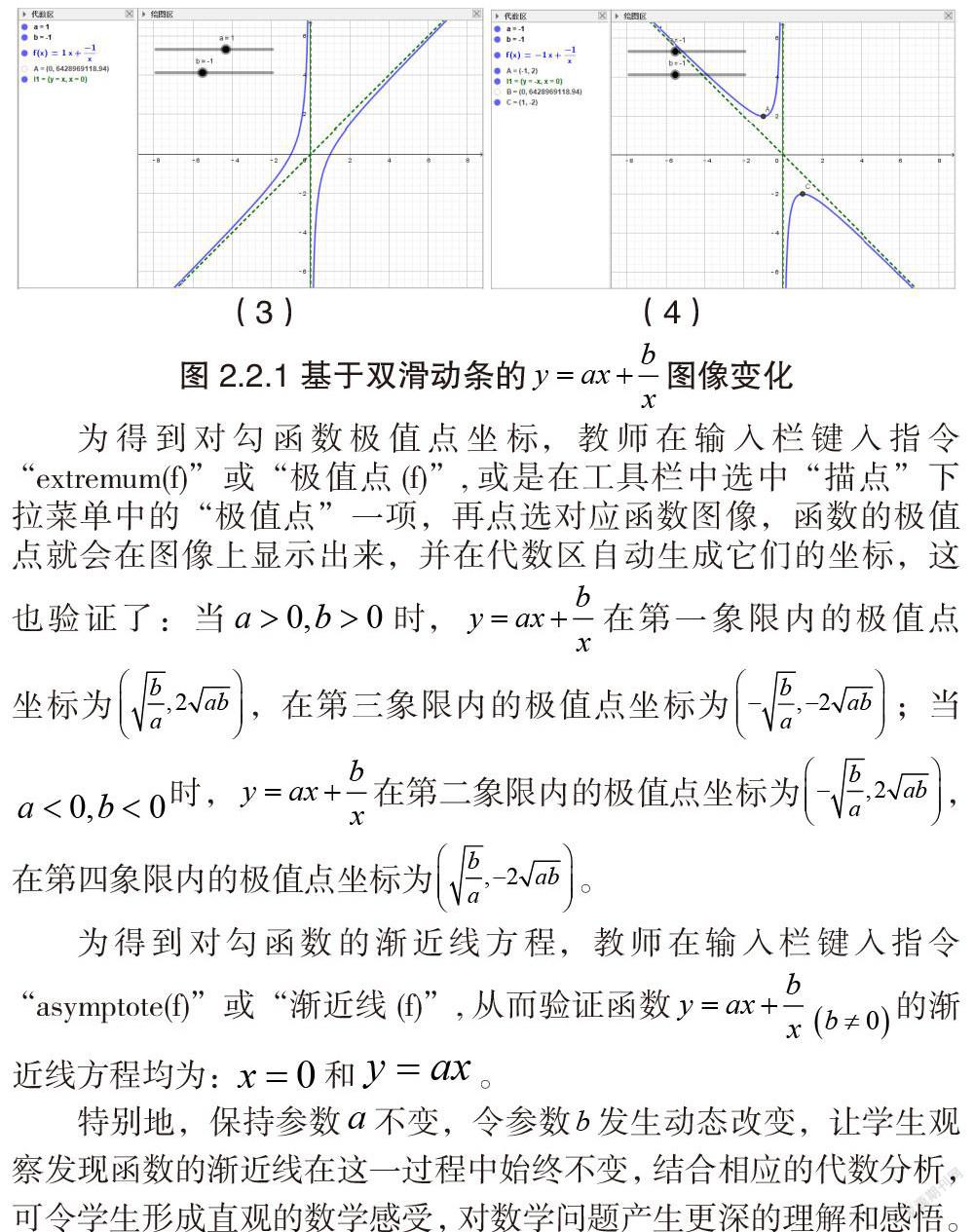
对勾函数的图像对于形成直观认识，分析这类函数的性质是十分重要的，因此采用信息技术手段进行图像的动态演示十分必要，教师通过GGB软件建立双滑动条，演示参数对于函数图像的动态影响过程（图2.2.1），和学生一起分析函数图像的变化规律。

为得到对勾函数极值点坐标，教师在输入栏键入指令“extremum（f）”或“极值点（f）”，或是在工具栏中选中“描点”下拉菜单中的“极值点”一项，再点选对应函数图像，函数的极值点就会在图像上显示出来，并在代数区自动生成它们的坐标，这也验证了：当时，在第一象限内的极值点坐标为，在第三象限内的极值点坐标为;当时，在第二象限内的极值点坐标为，在第四象限内的极值点坐标为。

为得到对勾函数的渐近线方程，教师在输入栏键入指令“asymptote（f）”或“渐近线（f）”，从而验证函数的渐近线方程均为：和。

特别地，保持参数不变，令参数发生动态改变，让学生观察发现函数的渐近线在这一过程中始终不变，结合相应的代数分析，可令学生形成直观的数学感受，对数学问题产生更深的理解和感悟。

3 结论

相较于传统的几何画板，GGB软件是国际上目前使用更加广泛的一种数学教学软件，实践结论表明利用GGB实施教学工作，进行函数图像的动态演示分析，有利于优化教学过程，从而提高教学的效率。

不仅是高中函数教学，GGB软件在其它课例、题目的讲解，甚至其它学科的教学中也会起到广泛作用，熟练使用这一软件对于一线教师提高课堂效率能够带来很大帮助，同时也可解决探究学习过程中存在的难点，培养学生学科思维，促进实践能力的提高、创新意识的发展。

参考文献：

[1] 中华人民共和国教育部制定.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020

[2] Dubinsky E， Mcdonald M A. APOS： A Constructivist Theory of Learning in Undergraduate Mathematics Education Research[M]// The Teaching and Learning of Mathematics at University Level. Springer Netherlands， 2002.

[3] Hohenwarter， M.， Preiner， J. Dynamic Mathematics with GeoGebra[J]. AMC，2007，10：12

[4] 孙娟.GeoGebra与几何画板的对比研究[J].中学课程辅导（教师教育），2016（10）：23.

[5] 金贤. Geogebra软件在高中数学教学中的应用[J]. 中学数学月刊， 2011（06）.