含沙空化对轴流泵内压力脉动特性的影响

林 鹏， 向林嵚， 胡 东， 翟松茂， 郭鹏程， 王 舒

（1.湖南人文科技学院 能源与机电工程学院，湖南 娄底 417000；2.宁波巨神制泵实业有限公司，浙江 宁波 315135；3.西安理工大学 水利水电学院，西安 710048）

轴流泵内部流动结构的变化，会引起流场的压力脉动特性以及泵机组振动特性的改变。

在压力脉动实验方面，宋希杰等[1]通过进行压力脉动特性试验探究进水漩涡对轴流泵装置影响的机理。陆荣等[2]采用高精度数字压力采集系统对一轴流泵模型的叶轮进口、导叶流道内和导叶出口进行压力测试，发现稳定工况下各监测点的压力脉动主频均为叶频。李彦军等[3]采用动态压力传感器对派河口泵站轴流泵装置模型分别在12种工况下进行了压力脉动试验，发现各监测点在各工况下的主频为叶片通过频率的整数倍频。González等[4]以离心泵为研究对象，通过试验研究了其内部的非定常流动特性，研究结果表明泵体振动与其压力脉动有着密切关系。文献[5-6]对离心泵和混流泵能量性能和压力脉动进行了实验测量和数值模拟，发现导叶进口预旋和叶顶间隙对泵的能量性能和压力脉动有着重要的影响。

在压力脉动数值模拟方面，万丽佳等[7]采用Mixture混合多相流模型，分析了不同颗粒浓度时的瞬时湍动能、压力脉动及径向力。张宁等[8]采用高频动态压力脉动传感器对离心泵压力脉动信号进行采集、分析，发现口环间隙对模型泵不同测点压力脉动特性的影响规律差异显著。张硕等[9]认为运行工况的变化会改变泵内流场的流动状态，从而对泵的振动特性产生影响。

此外，朱荣生等[10]、张德胜等[11-13]对螺旋轴流泵和轴流泵压力脉动进行了一系列试验及数值模拟研究，然而以上研究主要考虑清水介质下的压力脉动，对泵在含沙条件下的压力脉动研究较少。王志远[14]认为泥沙对双吸式离心泵压力脉动的影响规律整体上是非线性的；高超丹等[15-19]研究了颗粒粒径和浓度对离心泵、双流道泵压力脉动的影响，但未能得出粒径和浓度对压力脉动规律影响的一致性结论。目前，有关含沙空化下轴流泵内部压力脉动方面的研究鲜有报道。因此，在含沙空化状态下，研究泥沙浓度、粒径及空化对轴流泵压力脉动作用规律的影响具有重要意义。

1 轴流泵计算模型及方法

1.1 设计参数

以大型排水泵站中28CJ-70型立式轴流泵为研究对象，其设计参数如表1所示。

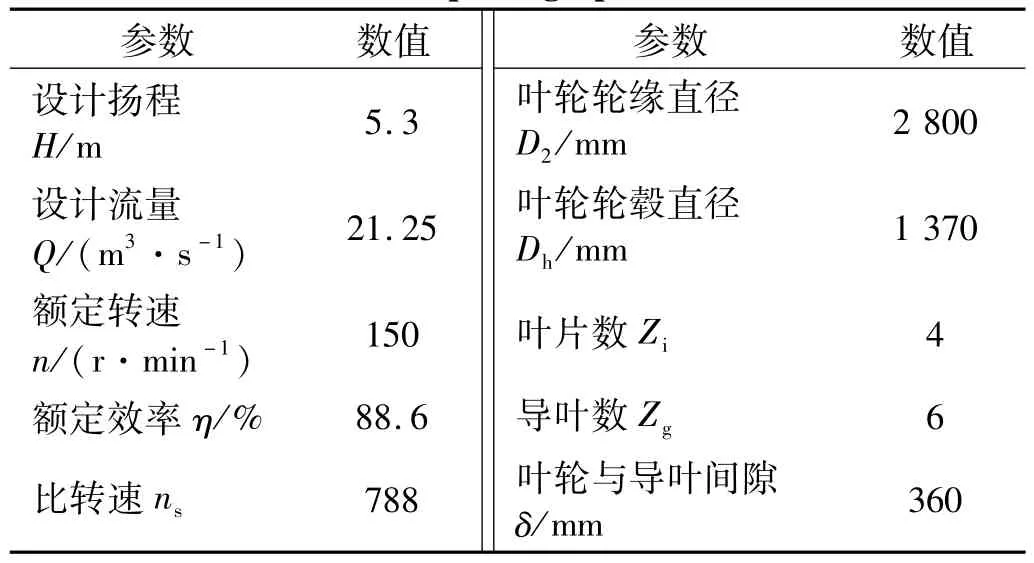
表1 水泵设计参数Tab.1 Pump design parameters

1.2 计算域及网格无关性验证

简化大型轴流泵进、出口流道，与泵段出厂试验情形相对应，计算域如图1（a）所示，整体网格划分如图1（b）所示。采用六面体结构化网格对泵模型进行网格划分，并进行网格无关性验证分析，如表2所示。当网格数量在700万左右时，泵扬程保持在5.34 m附近，随着网格数量的继续增加，扬程变化小于1%，考虑计算的经济性，最终选择方案2，确定网格总数为763万。

表2 网格无关性分析Tab.2 Grid independence analysis

图1 轴流泵模型和结构网格划分Fig.1 Axial-flow pump model and structural meshing

1.3 边界条件选择

采用基于有限体积法（control volume-finite element method，CV-FEM）[20]的ANSYS CFX流体仿真软件进行数值计算，离散方程使用全隐式耦合代数多重网格方法进行求解，计算收敛精度设为10-5[21-22]。两相流之间的相间传递选用颗粒轨道模型。边界条件设置为压力进口和质量流量出口，进口压力设为101.325 kPa，出口质量流量设置为21 186.25 kg/s。以清水无空化结果作为空化计算的初始值，选取25℃的水和水蒸气作为计算介质。

2 空化模型及外特性验证

2.1 空化模型

空化计算采用ZGB空化模型，它是一种由Rayleigh-Plesset方程推导发展而来，并得到广泛使用的空化模型[23]，兼容性较好，适用于计算不同泥沙浓度的含沙空化数值计算当中。从Rayleigh-Plesset方程推导得出空泡动力方程

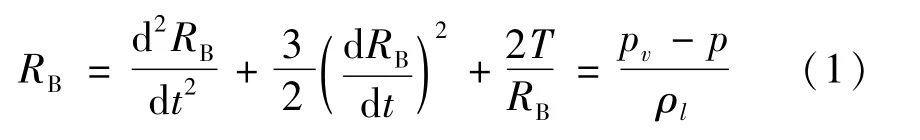
式中:RB为空泡半径；T为表面张力系数；pv为汽化压力。忽略二阶项和表面张力项，上述方程简化为

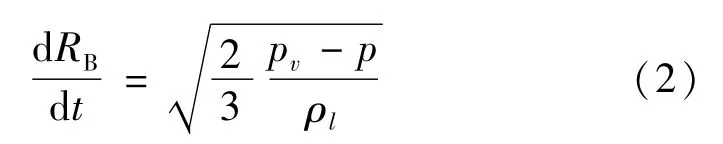
Zwart等采用单位体积空泡数n0求得总相间质量传输率R的表达式为

单位体积空泡数n0的表达式取决于相变的方向，对于空泡的生长（汽化），n0由式（4）给出

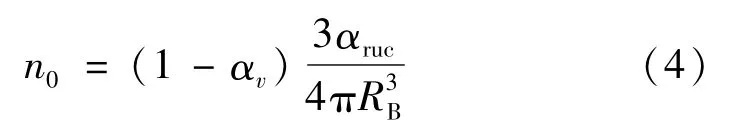
对于空泡的溃灭过程（凝结），n0由式（5）给出

把式（1）～式（5）合并即可推导得出空化模型的最后形式

式中:αruc为成核位置体积分数；Fvap为蒸发系数；Fcond为凝结系数。其中αruc=5×10-4，RB=1.0×10-6m，Fvap=50，Fcond=0.01。由于凝结过程通常要比蒸发过程慢得多[24]，故Fvap和Fcond并不相等。

2.2 外特性验证

图2为轴流泵分别抽送粒径d=0.5 mm、含沙量Cm=5%的含沙水和清水时的外特性计算值与清水试验值的对比图，其中，泵的外特性试验数据为泵段的出厂试验数据。根据笔者前期研究结果[25]，对比分析Standard k-ε，RNG k-ε，SST k-ω和Standard k-ω湍流模型的计算精度，发现SST k-ω湍流模型适用性最好。

图2 试验性能与预测性能对比Fig.2 Comparison of experimental performance and predictive performance

由图2可知，外特性计算值与试验值具有良好的一致性，说明轴流泵在输送清水和含沙水时，SST k-ω湍流模型在数值计算中具有很好的适用性。轴流泵输送含沙水时，其扬程和效率均略有下降；在设计工况下，相比清水计算值，加入泥沙后泵扬程下降5.93%，效率下降1.55%，小流量时的降幅（扬程下降6.68%，效率下降3.34%）大于其他工况。

3 压力脉动计算设置

3.1 监测点布置

计算监测点如图3所示。监测点P1～P5，P6～P10分别为泵入口与叶轮进口结合面和叶轮出口与导叶进口结合面上从轮毂到轮缘方向依次分布的点。

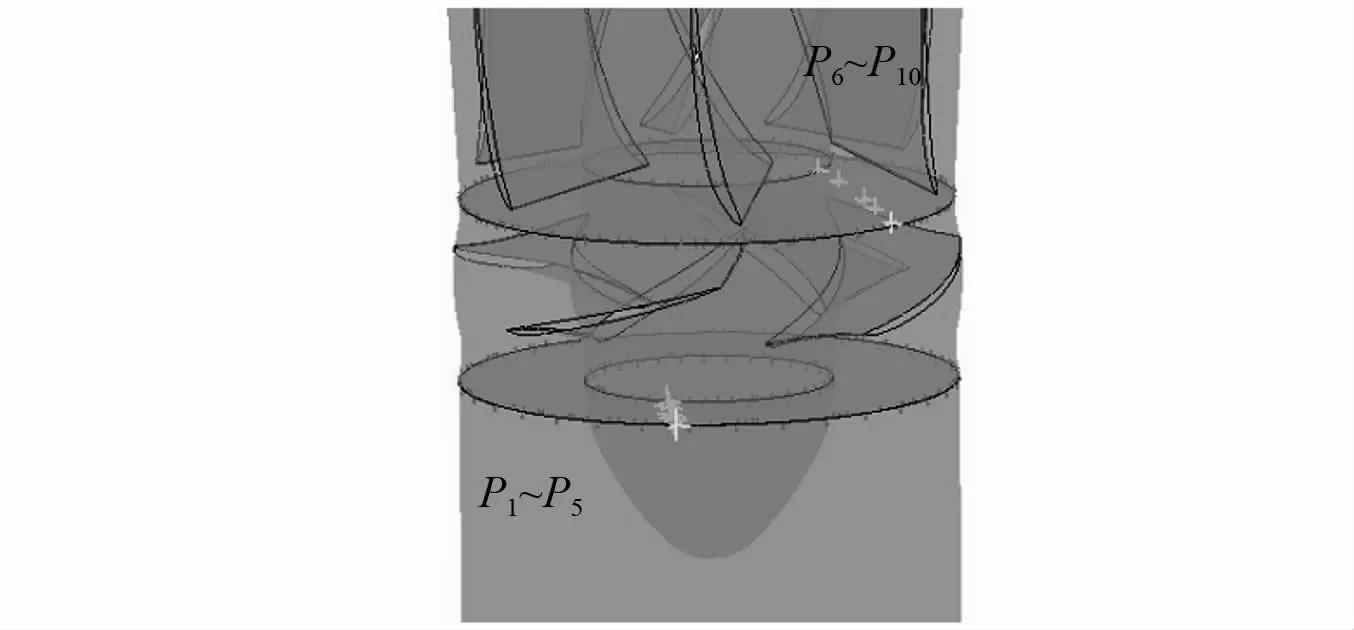
图3 监测点示意图Fig.3 Schematic diagram of monitoring points

3.2 压力脉动系数Cp

3.3 非定常计算设置

非定常计算需要设置时间步长，其选取跟转子的转速有关。其计算公式为周期T=60/n=0.4 s，设置每个时间步长为叶轮旋转4.5°所需的时间，则t=T/80=0.005 s，选取6个周期作为采样对象，则共需480个时间步长，其总时间为2.4 s。

3.4 无量纲参数定义

用无量纲半径rb（其定义参数如图4（a）所示）在叶轮表面选取5条不同的截面流线，如图4（b）所示，定义为

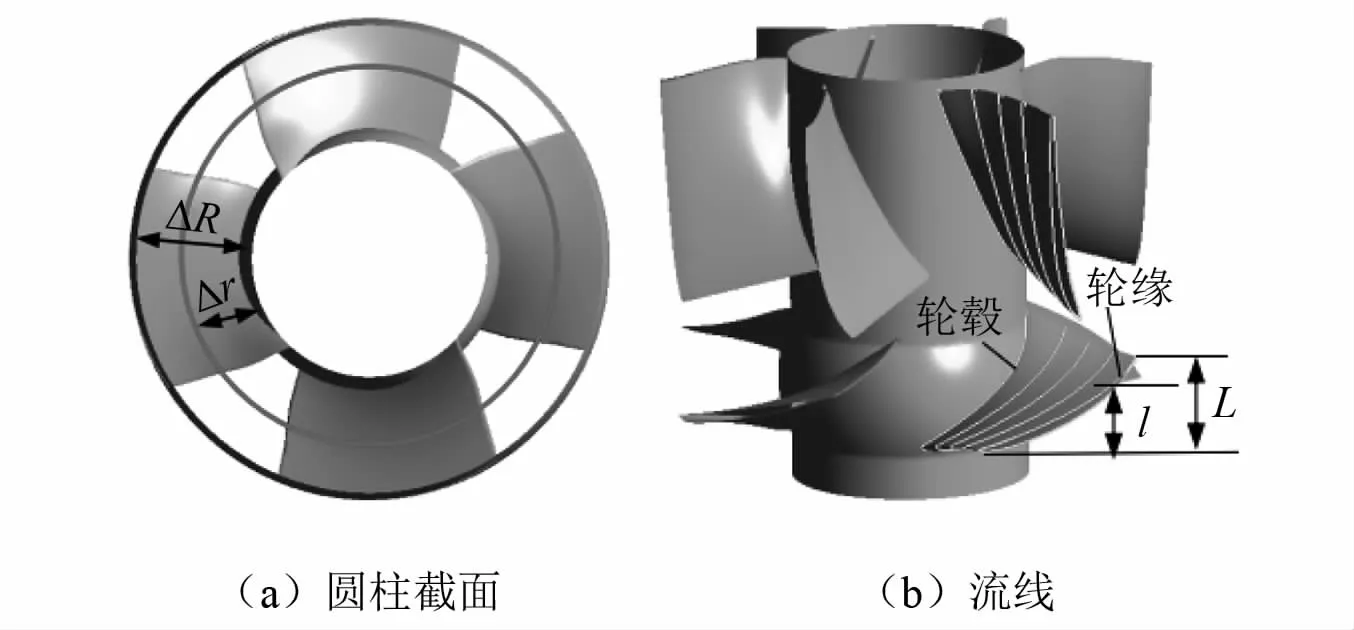
图4 叶轮截面流线及无量纲参数示意图Fig.4 Schematic diagram of flow lines and dimensionless parameters of impeller section

定义叶轮内无量纲距离δz

式中:Δr为所在圆柱截面与轮毂的距离，m；ΔR为叶片外径与轮毂的差值，m；l为所在截面到叶片进口的轴向距离，m；L为叶片出口到叶片进口的轴向距离，m。

4 计算结果分析

4.1 压力脉动时域分析

分别研究设计工况下，输送介质为清水和含沙水（含沙量Cm=5%，粒径d=0.5 mm）时，叶轮进口和出口监测点的压力脉动时域变化情况。

图5为清水、含沙水非空化和临界空化状态下压力脉动时域图对比。由图可知，无论是输送清水还是含沙水介质，临界空化状态下压力脉动系数明显大于非空化状态。当介质为清水时，在非空化状态下，压力脉动系数在-0.04～0.03内呈周期性波动；在临界空化状态下，压力脉动系数在-0.10～0.15内周期性波动，其波形与清水时不太一致，最大值为非空化状态的5倍，说明空化的产生引起了泵内流动结构的改变，破坏了流动的周期性和均匀性。

图5 非空化和临界空化状态下压力脉动时域图对比（C m=5%）Fig.5 Comparison of pressure pulsation time domain diagrams under non-cavitation and critical cavitation states（C m=5%）

当介质为含沙水时，压力脉动系数与清水时趋势一致，压力脉动系数在-0.050～0.035内波动，与清水时的波动幅度相近。说明，当含沙量较小时，泥沙对泵内部流动影响不大，不会引发较大的压力脉动升幅；在临界空化状态下，压力脉动系数在-0.3～0.3内呈非周期性波动，波形与非空化状态差距较大，最大值为非空化状态的8.6倍。说明，泥沙的加入促进了空化的发展，泵内流动结构进一步遭到破坏。

此外，清水和含沙水时，除监测点P1（进口轮毂）和P5（进口轮缘）压力脉动系数大于叶轮出口处外，其他点均小于叶轮出口处监测点压力脉动值；在临界空化状态下，叶轮出口处脉动系数均大于进口处，说明除空化外，叶轮与导叶的动静干涉是引发压力脉动的一个主要因素。

4.2 压力脉动频谱分析

为了更加直观的看到，输送介质和空化压力的改变对叶轮内压力脉动的影响，分别研究输送介质为清水和含沙水（含沙量Cm=5%，粒径d=0.5 mm）时，叶轮进口和出口监测点的压力脉动频率变化情况。

图6为轴流泵输送清水和含沙水介质时，非空化和空化状态下，不同位置监测点的频谱图。由图可看到，压力脉动幅值最大和较大处主要发生在低频区，并呈现周期性逐渐降低的趋势，且其最大和较大幅值均在通过频率的整数倍处产生[28]。这是因为在任何工况下，动静叶栅交界面处叶轮旋转都是产生压力脉动的主要原因，因此压力脉动的频率都为转频的倍数。最大幅值所在位置对应的频率可按式（11）进行计算

图6 非空化和临界空化状态下压力脉动频谱图对比（C m=5%）Fig.6 Comparison of pressure pulsation frequency domain diagrams under non-cavitation and critical cavitation states（C m=5%）

式中，fr=n/60=150/60=2.5 Hz。

叶轮转频（叶频）与叶片数有关，可用式（12）进行计算

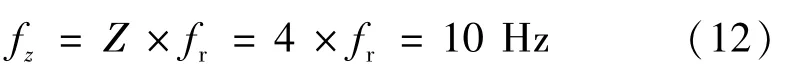
在输送清水时，最大脉动幅值为0.02，对应的频率主要为10 Hz，20 Hz，即振动频率为叶频和二倍频；临界空化时，最大幅值为0.04，对应的频率为2.5 Hz，10 Hz和20 Hz，即振动频率为转频、叶频和二倍频。

在输送含沙水时，压力脉动最大幅值对应的频率与清水时趋势一致，最大脉动幅值比清水时稍大；在含沙水临界空化状态下，最大幅值比清水空化大3倍，对应的频率为2.5 Hz，其他脉动频率主要为10 Hz和20 Hz，与清水空化相比，主要脉动频率一致。随着空化程度的加深，各监测点主频附近的谐频逐渐向低频段移动，与李彦军等的研究结果一致。

4.3 压力脉动系数Cp分布

图7为清水和含沙水介质下，非空化和临界空化状态下叶轮内压力脉动系数Cp分布图。由图可知，整体上看，压力脉动波动较大的位置为叶片进口和出口边附近，且进口边压力脉动系数大于出口边，工作面压力脉动波动小，背面压力脉动波动幅度较大，尤其是在泵发生空化时，背面压力脉动急剧增大，这是由于叶片背面存在局部低压区，空化首先在叶片背面产生，故叶片背面的压力脉动系数会存在大幅度的波动，与实际情况相符。

图7 非空化和临界空化状态下叶轮内压力脉动系数Cp分布（C m=5%）Fig.7 Distribution of pressure pulsation coefficient in impeller under non-cavitation and critical cavitation states（C m=5%）

从局部看，在清水工况下，压力脉动系数均匀分布在叶片表面，变化范围为-0.55～0.60；当发生空化时，工作面上Cp变化不大，背面Cp波动剧烈。

从轴向看，从叶片进口到叶片中后部，Cp变化较大，其值由负变为正；从径向看，Cp随叶轮半径的增大而增大，以轮缘处的波动最为显著。在含沙工况下，Cp的波动大于清水，未发生空化时，Cp的波动仅在叶片进口到无量纲距离0.2处；发生空化时，Cp的波动几乎覆盖了整个叶片背面，说明泥沙的加入对叶轮内的流态影响较大，使整个流道内的流动变得更加紊乱，会加剧空化的发展，引起泵内压力脉动加剧。

图8为清水和含沙水介质下，非空化和临界空化状态下导叶内压力脉动系数Cp分布图。由图可知，从宏观上看，相对叶轮而言，输送何种介质和是否空化对导叶内的压力脉动系数影响不大。

图8 非空化和临界空化状态下导叶内压力脉动系数Cp分布（C m=5%）Fig.8 Distribution of pressure pulsation coefficient in guide vane under non-cavitation and critical cavitation states（C m=5%）

从细部看，介质和空化主要影响导叶叶片进口，输送介质含沙时，叶片进口无量纲距离0.1位置处，背面Cp值有所增大；空化时，叶片进口背面处Cp值波动较大，这是由于导叶进口边处离叶轮出口最近，受叶轮内压力脉动的影响较大，因而，比起导叶的其他部位，进口处最为敏感，压力脉动系数的变化最先在此处呈现。因此，含沙量对导叶内的压力脉动影响不大。

5 结 论

分别研究清水、含沙水、清水空化及空化与泥沙磨损联合作用下，轴流泵内部压力脉动特性，得出以下主要结论:

（1）无论是输送清水还是含沙水介质，临界空化状态下压力脉动系数明显大于非空化状态。当含沙量较小时，泥沙对泵内部流动影响不大，不会引发较大的压力脉动升幅；在临界空化状态下，压力脉动幅值明显增大。说明，泥沙的加入会加剧压力脉动，且促进空化的发展。叶轮出口处脉动系数均大于进口处，说明，除空化外，叶轮与导叶的动静干涉是引发压力脉动的一个主要因素，空化会增大压力脉动，对泵的振动造成不利影响。

（2）在无空化状态下，最大脉动幅值对应的频率主要为10 Hz，20 Hz，即振动频率为叶频和二倍频；临界空化时，最大幅值对应的频率为2.5 Hz，10 Hz和20 Hz，即振动频率为转频、叶频和二倍频。

（3）压力脉动波动较大的位置为叶片进口和出口边附近，且进口边压力脉动系数大于出口边，工作面压力脉动波动小，背面压力脉动波动幅度较大，尤其是在泵发生空化时，背面压力脉动急剧增大，这是由于叶片背面存在局部低压区，空化首先在叶片背面产生，故叶片背面的压力脉动系数会存在大幅度的波动，与实际情况相符。