内肋骨长舱段塑性总体稳定性计算方法研究

邱昌贤，黄进浩，秦 天，王 琨

（中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

由各国潜艇结构的现状与发展趋势可见，基于大分舱思想的单壳体长舱段结构形式是一种成功的设计方案，可显著减少轻外壳、舷间结构及内部舱壁的重量和装配、焊接施工量，并为大型设备、模块化平台的纵向进舱提供了极大便利，舱壁的减少也有利于线缆、管路的总体布置。单壳体圆柱壳舱段通常采用内肋骨形式，与外肋骨相比，避免了肋骨受海水双面腐蚀的不利状况，其翼缘应力有所增大，但结构总体稳定性理论上会比外肋更好，长舱段的长径比（耐压壳长度/直径）往往比小分舱舱段大一倍以上，为保证总体稳定性，常设置一根或多根特大肋骨（heavy frame）进行加强，因此耐压结构设计需要解决普通肋骨内置且带特大肋骨的单壳体长舱段结构的总体稳定性计算问题。

20世纪中叶起，英国的Kendrick博士[1]曾基于薄壳稳定性理论研究了带中部强肋骨的环肋圆柱壳外压屈曲问题。美国Taylor水池进行过大分舱环肋圆柱壳的精车模型试验研究[2]，采用14道工序将中部特大肋骨切削为不同的截面形状，分别进行无破坏试验（避免材料进入塑性），以检验具有不同扭转、弯曲刚度的强肋骨的加强效果，试验中基于弹性应变测量数据用Southwell法推算临界压力，该值与实际破坏压力的误差在4%以内[3]，验证了强肋骨能代替重量大得多的内部舱壁对长舱段起到支撑作用。Baruch和Singer[4-5]研究了肋骨偏心对端部简支圆柱壳弹性失稳压力的影响，认为与外肋相比，内肋能将临界压力提高10%～15%。以上研究工作均局限于弹性稳定性范畴，虽然取得了很有价值的学术成果但工程实用性不强。

近年来，国内一些研究者基于规范方法和有限元分析，也得到了一些有意义的结论。丁海旭[6]对若干精车模型进行了弹性稳定性计算，给出了大肋骨与普通肋骨惯性矩之比与舱段总体稳定性的关系；何福志[7]对Taylor水池的长舱段模型进行了有限元分析，根据总体失稳压力—框架肋骨惯性矩关系曲线搜索大肋骨最优结构参数；宋世伟[8]采用Abaqus分析了环肋圆柱壳长舱段的稳定性规律，研究了现行规范在不同参数范围内的求解适用性；邱昌贤[9]基于矩形截面压杆的双模量理论和高强度钢的材料弹塑性本构关系，建立了环肋圆柱壳结构总体稳定性塑性修正曲线及修正方法。

参照国内外文献及研究经验，针对现有方法的局限性，作者在结构上考虑肋骨偏心的影响，在材料上考虑高强度钢的弹塑性本构关系，利用Ritz法对环肋内置且含特大肋骨的单壳体长舱段结构在静水外压下的弹塑性稳定性计算方法进行理论研究，分别基于J2流动理论和形变理论建立了结构小挠度弹塑性失稳压力的迭代计算方法，编制了运算程序，针对长径比为1.5～3.1的高强度钢模型进行了理论计算和有限元数值仿真分析工作，获得了塑性阶段的模型总体失稳破坏压力。本文方法给出的结构总体稳定性计算值与有限元结果符合较好，可使耐压结构的尺寸和重量设计更为优化。本文的计算方法经初步验证是合理和可行的，所得研究成果和相关结论可为单壳体长舱段结构的稳定性机理剖析提供技术支撑和参考建议，也为现行规范方法的修改完善及在设计中确定合理的尺寸参数和安全储备打下了基础。

1 圆柱壳长舱段结构弹塑性稳定性计算方法

1.1 弹塑性失稳系数

经典的材料塑性理论将单向拉伸曲线推广到复杂的三维应力状态，目前对塑性屈曲问题采用的本构关系主要有2种：塑性等向强化的J2流动理论（塑性增量理论）和J2形变理论（塑性全量理论）。增量理论建立应力增量和应变增量之间的关系，全量理论认为应力和应变存在一一对应的函数关系，二者均可通过引入弹塑性失稳系数[aij]来建立统一的广义应力、应变关系[10-11]：

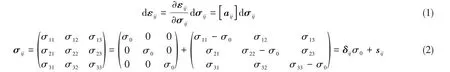
材料应变由弹性和塑性部分组成，其中弹性应变可由广义Hooke定律得到：

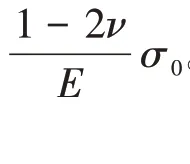
获得弹性应变增量的表达式后，再根据J2流动理论推导材料进入塑性后的应力应变增量关系，即可得到弹塑性应力—应变增量之间的关系式[10]：

式中，h(J2)可由顺x轴的单向拉伸试验确定，σij在除x轴以外的方向为0，σ0=σx/3。

将εij（i，j=1，2，3）分别按式（4）展开可得6个方程，再代入式（3）～（4）等表达式进行变量代换，整理后可得对称的弹塑性失稳系数矩阵[aij]（i，j=1，2，3，4，5，6）。

根据J2形变理论，材料应力、应变之间的弹塑性关系为

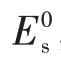
同理，将εij（i，j=1，2，3）展开后可得对称的系数矩阵[aij]（i，j=1，2，3，4，5，6）。

全量、增量理论的弹塑性失稳系数矩阵[aij]形式相似，对潜艇耐压圆柱壳结构，可忽略法向应力σz，则广义三维应力状态退化为平面应力状态，再根据Kirchoff直法线假设，剪应力τzy、τzx为0，从而使[aij]的形式大为简化。

为方便计算，假定失稳前耐压圆柱壳处于无矩状态，横向剪应力τxy为0，计算周向应力时将肋骨截面积平均分配到壳板上，经推导可得具体形式进一步简化的失稳系数[aij]，再用[bij]将应力-应变关系改写为

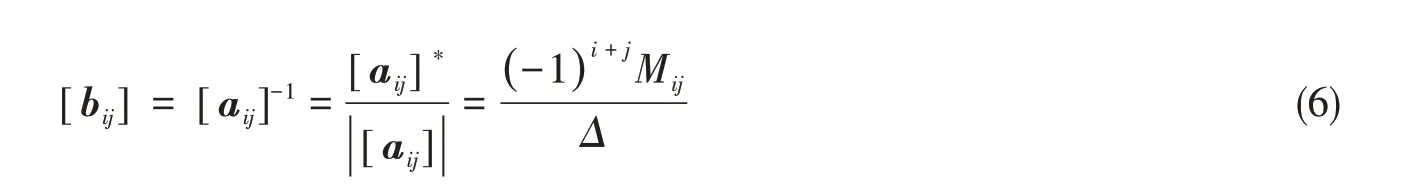
1.2 考虑肋骨偏心的塑性稳定性计算方法

塑性稳定性计算时取坐标原点在圆柱壳端部中曲面上，设x、y、z分别为纵向、周向和径向坐标，u、v、w分别为纵向、周向和径向位移，径向坐标和径向挠度均以指向圆心为正，圆柱壳失稳时满足简支边界条件的形函数[10-14]取为

利用1.1节推得的弹塑性系数[bij]，结构按平面应力状态并仅考虑小挠度，分别计算耐压壳板的弯曲及中面应变能V1、V2的应变能：

普通肋骨及特大肋骨均可简化为单向应力状态，其位移函数与圆柱壳体相同。为考虑截面偏心影响，肋骨横截面上任一点的周向应变值根据该点的径向坐标来确定：

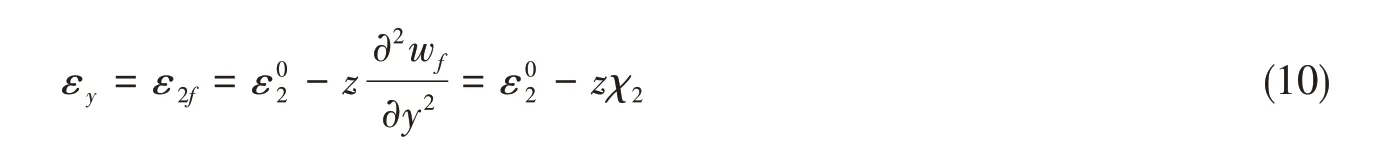
经推导，对距离坐标原点x=il处的第i根肋骨，其结构应变能为

式中，yci为第i根环肋计及带板宽度为l（特大肋骨取为与规范相同的2l）的组合截面形心的径向坐标，Rfi为截面形心半径，Ii为截面惯性矩，I0i为第i根环肋自身惯性矩，Fi为肋骨横剖面面积，y0i为肋骨中和轴到壳板表面的距离，y0i+0.5t=efi，t为板厚。式中引入系数k2=1或0以分析肋骨压缩应变能的影响。根据相关理论研究，肋骨截面的扭转、翘曲和面外弯曲的应变能对环肋圆柱壳弹性失稳压力的影响很小[2]，计算中予以忽略。

求得结构各部分能量后再计算水压做功，从而可建立能量平衡方程。根据能量原理，结构总能量П取极小值的条件是П对A、B、C的偏微分为0，由此得到如下齐次线性方程组：

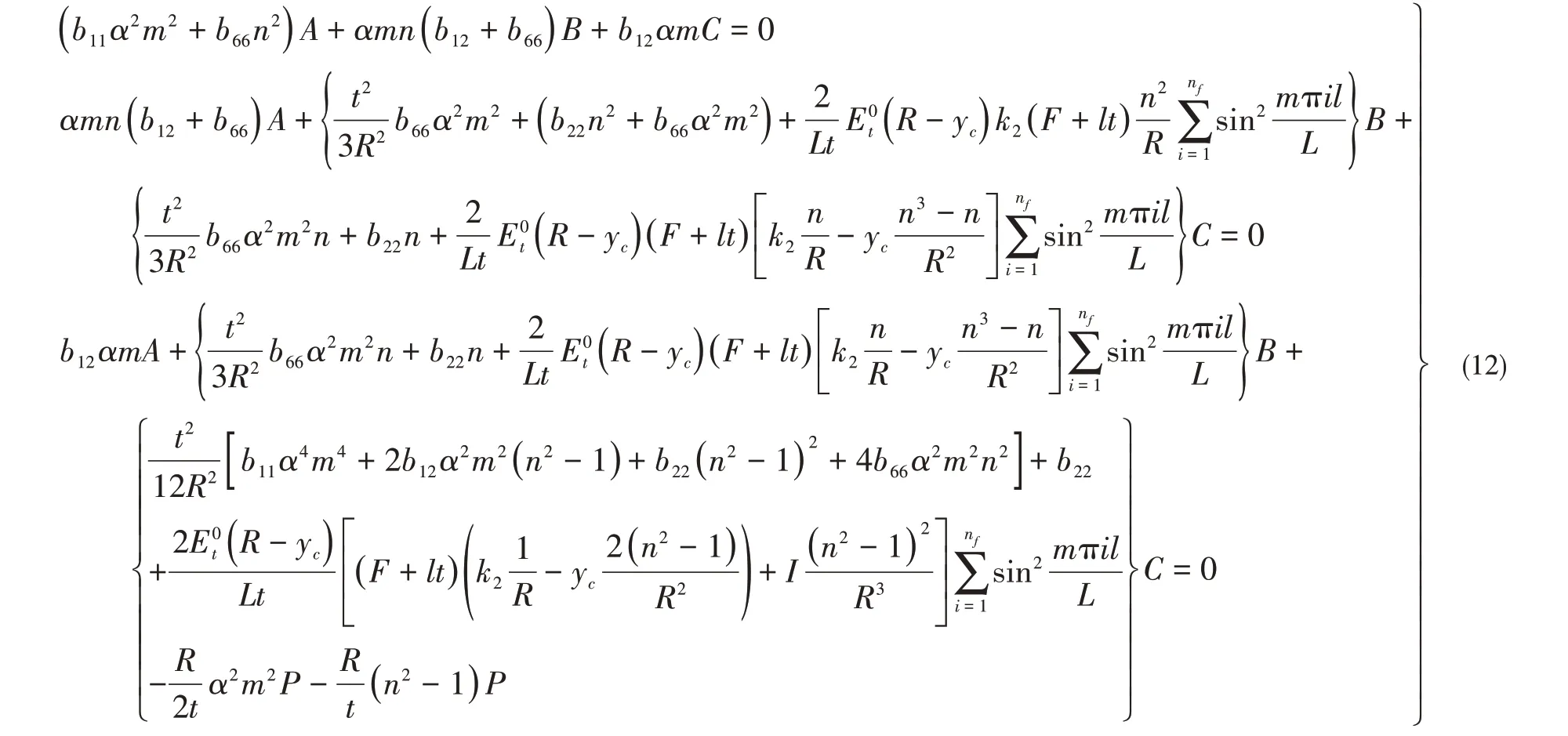
此方程组存在非零解的充要条件是系数行列式为0，这个矩阵是对称的，cij=cji。

利用能量法计算单壳体长舱段结构的弹塑性失稳压力时，首先将割线模量Es和切线模量Et取为弹性值，则[bij]退化为弹性失稳系数，求得与弹性临界压力对应的等效应力强度，若高于材料比例极限，则在附近选定一个应力强度计算相应的Es和Et（Es和Et可根据高强度材料单向拉伸试验的弹塑性本构关系确定），再通过迭代求解塑性失稳压力。

带特大肋骨的单壳体长舱段结构的弹塑性总体失稳形式既可能表现为含大肋骨的舱段失稳（一般周向整波数n=2），也会发生在大肋骨之间的舱段上（一般周向整波数n=3）。本文的计算方法对以上二者均可适用，并可方便地推广至含多根大肋骨舱段的稳定性计算，或退化为无大肋骨舱段的状态。

2 模型计算结果对比分析

为了验证理论方法，对内肋骨长舱段模型进行了有限元建模和数值计算，其结构形式为T型内环肋圆柱壳，舯部采用内置T型特大肋骨加强，大肋骨根部耐压壳板进行了局部加厚，材料为高强度钢。所计算模型的主要结构参数为：舱段长径比L/D=3.14，特大肋骨与普通肋骨惯性矩比Ihf/If=41.42，圆柱壳半径与厚度之比R/t=106.75。

本文利用所建立的方法和程序对圆柱壳长舱段模型的结构塑性总体稳定性进行了计算，迭代算法收敛速度很快且结果精度较高，如图1所示。

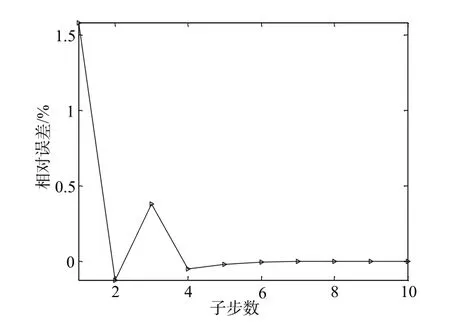
图1 长舱段结构塑性稳定性迭代计算中各子步误差Fig.1 Error value in every substep of the buckling calculation

为评估理论计算方法的合理性，本文还采用了形式较为简洁的规范公式、修正曲线和ANSYS有限元程序进行计算，并展开结果对比，如图2和表1所示。

图2 单壳体长舱段结构有限元模型及塑性总体失稳数值计算结果Fig.2 FE shell model and numerically-analyzed results for general instability

表1 模型塑性总体失稳压力计算结果（MPa）Tab.1 Models’calculated critical pressure of plastic general stability(MPa)

对于大肋骨之间的舱段塑性总体稳定性，与有限元结果相比，规范计算值偏保守一些，本文理论方法的计算值接近且略高于有限元分析结果，初步验证了方法是合理、可用的，4个算例的结果表明，流动理论与形变理论的计算结果有所不同，但差别不大。

对于包含舯部特大肋骨在内的模型结构塑性总体稳定性，与有限元解相比，失稳临界压力的规范解（8.37 MPa）略偏保守，导致为了满足总体失稳压力的控制标准，需额外提高特大肋骨的刚度，由此产生的冗余重量和尺寸将不利于结构优化和设备布置。本文理论方法的计算值相对合理，若能保证其可靠性，则可使耐压结构的尺寸和重量设计更为优化，但该方法尚需得到更多试验结果的验证和支撑。

3 结 语

本文参照国内外研究经验，针对现有方法的局限性，在结构上考虑肋骨偏心的影响，在材料上考虑高强度钢的弹塑性本构关系，利用Ritz法对环肋内置且含特大肋骨的圆柱壳长舱段结构在静水外压下的弹塑性稳定性计算方法进行了理论研究；基于流动理论和形变理论建立了结构小挠度弹塑性失稳压力的迭代计算方法，计算结果精度较好，工程实用性较强；同时针对长径比为1.5～3.1的高强度钢模型进行了有限元数值仿真分析，计算和对比了塑性阶段的模型总体失稳破坏压力，本文方法给出的结构总体稳定性计算值与有限元结果符合较好。

本文理论计算方法经初步验证是合理和可行的，给出的总体失稳压力计算值比规范方法更符合高强度钢模型有限元计算结果。方法的通用性较好，既可方便地推广至含多根大肋骨舱段的稳定性计算，也能退化为无大肋骨舱段的状态。圆柱壳长舱段结构的总体失稳形式无论是包含大肋骨的舱段失稳，还是在大肋骨之间的舱段失稳，规范方法给出的计算结果都比较保守，从而导致结构增加冗余重量和尺寸。本方法可使耐压结构的设计更为优化，但方法的可靠性尚需得到更多试验结果的验证和支撑。

按单向应力状态计算肋骨应变能的方法在肋骨腹板增高后或存在适应性问题，特大肋骨自身的侧向稳定性机理尚待研究，内、外肋骨圆柱壳总体稳定性的差异需要模型试验的充分验证。关于几何非线性对结构弹塑性稳定性的影响，本文沿用了规范的修正方法，建议在此领域开展深入探讨。结构大挠度的影响也需进一步研究。