基于粒子群优化算法的超长距传输系统拉曼放大器特性研究

隋 亮，陈跃第，赵 涵，殷雪莉，曾 程

（1.南方电网能源发展研究院有限责任公司，广东广州 511458；2.中国电力工程顾问集团西南电力设计院有限公司，四川成都 610056）

电力通信网络系统传输距离长，尤其是特高压变电站之间的距离通常超过300 km。超长距传输系统可实现端到端的直连通信，线路中间不需要任何中继设备，这不仅降低了建设成本，也减少了故障点，使系统在降低了综合运维成本的基础上提高了传输可靠性。

拉曼放大器是解决长距离电力传输的关键器件之一，其最优结构的分析与定型具有重要的意义。文中针对电力通信超长距传输系统中应用的拉曼放大器进行了建模分析，引入改进的粒子群算法求解了其最优结构，并通过实验验证了算法的有效性。

1 拉曼放大器最优结构分析

拉曼放大器结构如图1 所示，对于前向拉曼放大器部分，信号光经过隔离器后进入WDM3，不同波长的泵浦光经过WDM1 后进入WDM3，合波后的信号光与泵浦光在光纤中完成信号放大；对于后向拉曼放大器部分，不同波长的泵浦光经WDM2 后进入WDM4，最终进入光纤完成对信号光的放大。在增益光纤中，完成放大后的信号进入WDM4，经隔离器及滤波器后从输出口输出。其中，隔离器用于消除反射光对泵浦光源的影响，同时避免信号反向传输。所用到的WDM 用于将信号光和泵浦光复用到同一根光纤中，或从同一根光纤中将信号光和泵浦光解分开来。所用的滤波器为窄带滤波器，用于滤除信号光以外的噪声，从而降低系统噪声。在实际工程中，常使用后向泵浦结构，即后向拉曼放大器[1]。

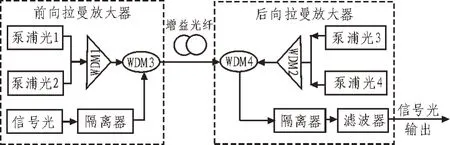
图1 拉曼放大器结构简图

放大器增益D的表达式为：

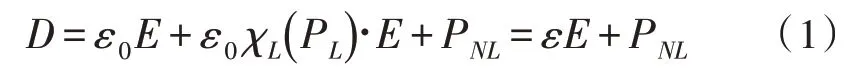
式中，ε为相对介电常数，ε=ε0(1+χL)，χL为线性电极化率张量，ε0为真空中的介电常数，PL与PNL为考虑非线性相互作用情况下极化强度的线性项与非线性项。

另外，由于拉曼散射属于三阶非线性效应，根据Maxwell 方程，非线性项可以写成[2]：

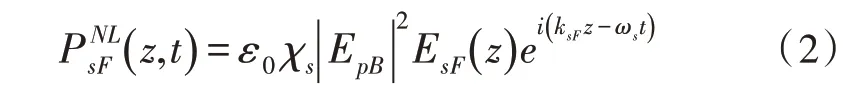
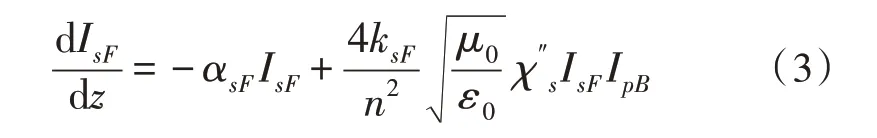
后向入射泵浦光的传输方程为：

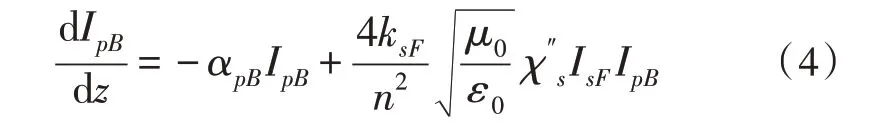
式中，IsF、IpB分别为后向泵浦光与前项传输信号光的光场强度。通过定义拉曼增益系数可得，拉曼耦合方程为[4]：

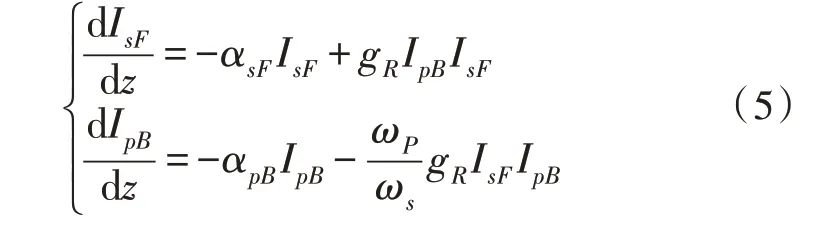
其中，ωP为泵浦光的频率。以上过程为拉曼放大器相互作用的描述形式。由式（5）可得，在拉曼放大过程中，信号光在沿光纤传输功率衰减的同时，泵浦光功率的一部分能量转移到信号光。而泵浦光则随着沿光纤传输衰减的同时，也将能量转移给信号光。

类似地，拉曼放大过程可以通过以下微分方程来描述：

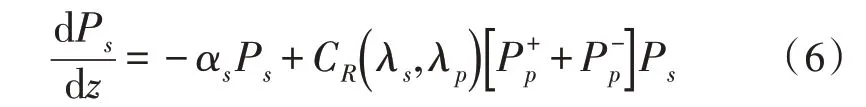
其中，Ps、Pp分别为信号光和泵浦光的光功率，αs为光纤的衰耗，CR为光纤的拉曼增益效率系数。、分别表示前向泵浦方式与后向泵浦方式的泵浦光功率。根据定义，拉曼放大器的开关增益可以写作：

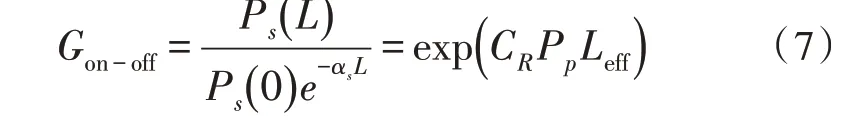
2 基于粒子群算法的最优结构求解

对于式（7）所示的最优结构求解问题，其本质为优化问题，用经典方法解决优化问题给计算机资源带来了较大的困难。文中在标准粒子群算法的基础上进行改进，以实现高效准确的最优结构求解。

标准的粒子群问题（即受群体行为的启发，其中元素在诸如搜索食物和防御的操作过程中具有同步运动的特征）[5]在粒子群中，每个粒子均流经多维搜索空间，并根据个体和全局的内存情况来动态调整其在搜索空间中的位置。因此，粒子利用自身及其邻居遇到的最佳位置，将自身更新为最佳解，并可基于优化问题的目标函数来评估得到每个粒子的适应度[6]。文中定义在迭代k时，下一个样本k+1 中第i个粒子的速度可表示为：

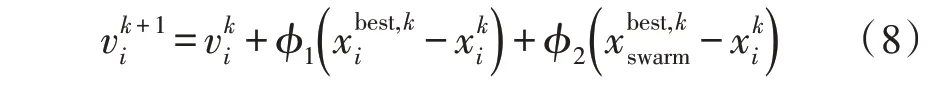
计算速度后，每个粒子的新位置可计算为[8]：

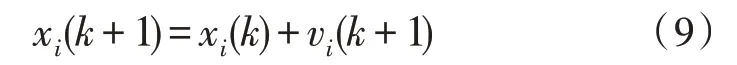
使用式（8）与式（9）重复执行粒子群算法，直到满足停止标准为止。粒子群提供了一种高效、鲁棒且简单的求解算法[9]。然而，由于缺乏速度控制机制，标准算法可能仅探索其局部区域，从而只能取得局部最小值。在较大速度的情况下，标准算法可能会使粒子离开边界定义的约束，导致求解问题发散[10]。文中使用了控制算法的收敛速度改进方法，引入代表粒子记忆的参数[11]。

拉曼放大器的最优结构求解是涉及特定问题约束的优化过程。文中定义增强拉格朗日粒子群（AL粒子群）和性能指标如下[12]：

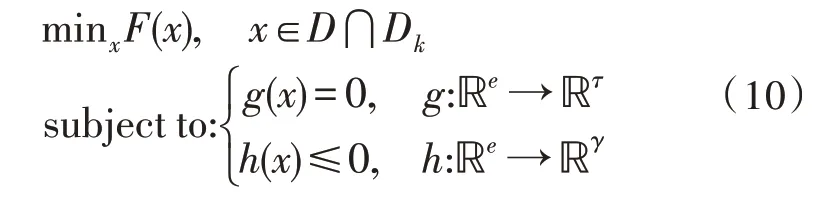
其中，F(x)是服从非线性方程g(x)与不等式约束h(x)的非线性目标，D表示可行区域，而Dk∈Δk表示搜索空间，使得＜x＜。其中，和是x的上下边界[13]。

文中改进的粒子群算法步骤如下：

步 骤1：令j=0,k=0，σ=zeros(1,τ+γ)，β0=β0∈Rτ+γ，并随机初始化群[14]。

步骤2：根据上文定义，建立每个粒子的L(x,σ,β)。

步骤3：检查终止标准，即是否大于适应性评估次数。若满足条件，则令，β=β*x[15]。

步骤4：求解预定义的最大迭代kmax。

步骤5：更新σj和βj，并令j=j+1 和k=0[16]。

步骤6：重复进行步骤2。

3 实验验证

为了验证所提算法的有效性，设置标准粒子群算法，如图2(a)所示，按照上文优化后的粒子群算法如图2（b）所示。针对不同入射泵浦光功率对拉曼放大器增益的影响，及不同光纤对拉曼放大器的增益的影响两个问题做了实验验证与分析。实验连接简图如图3 所示。

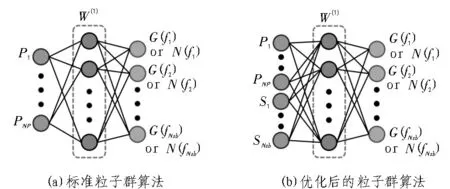
图2 算法结构原理示意图

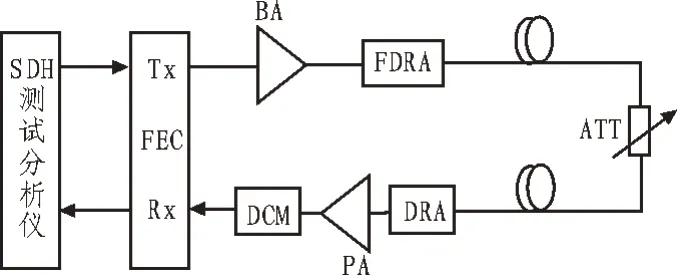
图3 泵浦功率对拉曼增益影响实验连接简图

所用的SDH 测试分析仪为Agilent 生产的N4906A版本，支持频率为2.5～10 GHz的SDH 信号测试。实验中使用的光纤为普通单模光纤，光纤长度为253 km，包含可调衰减故有衰耗及接头衰耗，线路总衰耗为51.80 dBm。

实验中，首先关闭前向及后向拉曼放大器，设备功率放大器（BA）的输出功率值为14.00 dBm。调节可调光衰，直到SDH 测试分析仪出现误码告警为止。此时可调光衰的衰耗值为4.20 dBm，前置放大器接收光功率为42.00 dBm。因此，在关闭拉曼放大器的条件下，系统最大支持衰耗值为56.00 dBm。调节前向拉曼放大器泵浦功率，步长为50 mW，相应地调节光衰数值，使SDH 测试分析仪处于临界状态，并保持15 min 无误码告警出现，然后记录不同功率下对应的可调光衰衰减值，再减去初始值。通过Matlab 绘制拉曼增益与泵浦功率之间的变化趋势，如图4 所示。

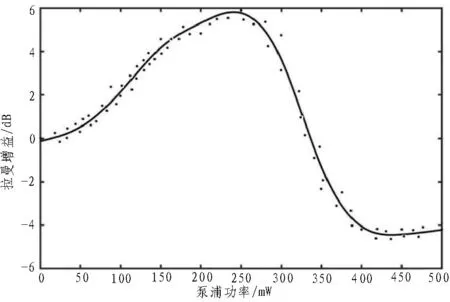
图4 前向拉曼放大器变化拟合曲线

由图4 中泵浦功率与拉曼增益对应的曲线走势可知，随着泵浦功率的增加，前向拉曼放大器的增益随之增加。但增加的速度随泵浦功率的增加而减小，最终达到增益饱和。随着泵浦功率继续增加，拉曼增益呈降低趋势，最终由于拉曼放大器泵浦功率过高，导致光信号被破坏，无法再进行传输。

在前向传播研究的基础上，分别选用普通单模光纤（Single Mode Fiber,SMF）、色散补偿光纤（Dispersion Compensation Fiber,DCF）及色散位移光纤（Dispersion Shifted Fiber,DSF）3种光纤进行测试。实验开始前，调节功率放大器，使输出光功率为14.00 dBm，调节可调光衰的衰减值，使系统处于临界状态，并使SDH 测试分析仪15 min 内无误码告警，记录此时可调光衰的衰减值。根据不同光纤条件下的初始可调光纤衰减值选择不同的光纤作为传输载体，重复上述实验过程，并记录此时可调光衰的衰减值以及与初始值的差值。利用Matlab 软件绘制不同光纤中泵浦功率与拉曼增益之间的关系曲线，如图5所示。

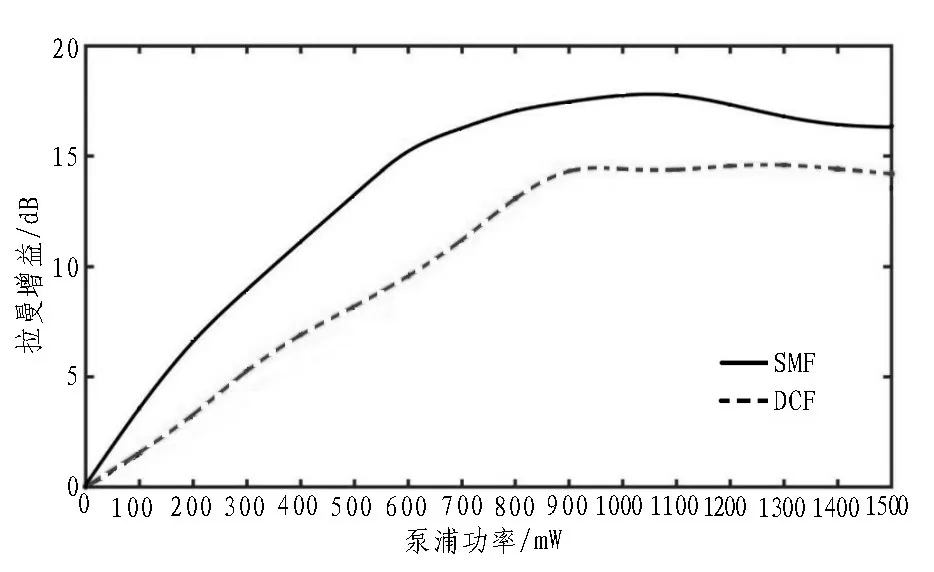
图5 拉曼放大器增益与泵浦光功率曲线

由图5 可看出，普通单模光纤（SMF）中GeO2与SiO2的比例较低，光纤中杂质含量较低，而色散补偿光纤（DCF）中GeO2与SiO2的比例在3 种光纤中最高。因此，通过分析粒子群算法可知，不同光纤中的拉曼增益效率由光纤中GeO2与SiO2的比例决定。在一定比例范围内，随着GeO2与SiO2比例的增大，拉曼增益效果随之增长。但在实际工程应用中，由于普通单模光纤具有更低的衰耗系数、更加成熟的制造工艺及更低的成本，仍是目前最常用的类型。

4 结束语

文中通过对拉曼放大器增益与泵浦功率进行实验研究，得到了拉曼放大器增益与泵浦功率之间对应的曲线关系。通过引入粒子群算法，得出拉曼放大器最优结构的求解方法，并通过实验得出了最佳工艺的拉曼放大器结构。文中的优化问题建模为线性系统，在未来的研究中，将主要致力于把最优结构求解问题转换为非线性问题。提高分析精度，进一步提升拉曼放大器的特性研究水平，对提高长距离输电的技术水平具有一定的工程意义。