基于多网格技术的电网工程造价数据信息分析方法研究

丁艳，张海文，孙永彦

（国网甘肃省电力公司经济技术研究院，甘肃兰州 730050）

对电网工程造价数据的有效分析，是电网建设中不可或缺的重要环节。电网造价的合理性对于实现电网项目的效益最大化具有重要意义。建筑成本指数（CCI）已被广泛用于衡量建筑行业的成本趋势[1]。CCI 为估算施工成本，在建设项目的规划阶段准备预算以及在施工阶段进行成本管理与控制提供了重要的参考信息。

准确的电网工程数据分析模型需要考虑到大量的数据变量，因为这些变量是人工、材料与设备成本的加权组合[2]。然而在使用因果模型分析CCI 时，模型的输入变量也是未知的，因此必须进行准确估计。此外，单变量时间序列模型由于受其先前值的动态影响，因此该模型并未利用来自于其他变量的信息[3]。这些问题对于分析电网工程造价成本的不确定性尤为重要。

为了克服因果关系与单变量时间序列模型的缺点，文中利用协整矢量自回归（VAR）模型来分析CCI。协整的VAR 模型可以更有效地应用于成本趋势的随机预测，可以轻松地将其他变量纳入成本预测和风险评估中，还可以描述变量的动态行为以及变量之间的长期与短期相互作用。

1 模型设计与计算原理

为对工程造价数据进行分析，文中使用了基于固定时间序列的VAR 模型。

1.1 VAR模型建立

工程造价数据的静态VAR 模型定义如下：令Yt=[y1t,y2t,…,ynt]' 表示时间序列变量的(n×1)向量，假定其表示平稳过程。基本的p阶滞后VAR 模型可定义为：

其中，t=1，2，…，T；C为n×1的截距项；A是n×m的系数矩阵；D是m×1的说明变量；εt为n×n的系数矩阵。文中使用一个简单的双变量VAR 模型，可以表示如下：

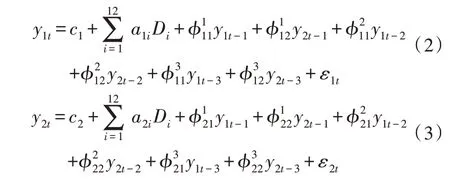
其中，Di(i=1,2,…,12)表示季节虚拟变量。虚拟变量反映了不同月份对变量CCI 与CPI的季节性影响。残差ε1t=ε2t=Cov(ε1t,ε2s)=σ12。协方差矩阵可以描述如下：

该模型的每个方程均具有相同回归变量的特征。尽管该文方法采用过去的CCI 和CPI 来分析预测未来的CCI，但是通过合并其他可提供的有用信息来预测电网工程成本的变量，使该文的VAR 模型变得非常灵活。

当两个变量之间存在某种协整关系时，协整VAR 模型存在如下关系：

其中，(y1t-1-β2y2t-1)为协整方程；系数β2为归一化的协整向量；系数θ1与θ2为调整后的参数。协整方程表示两个变量之间的协整关系或长期稳定关系的偏差。当两个变量均不具有长期关系时，调整系数θ1与θ2将模型推回到长期均衡。协整VAR 模型不仅考虑了长期影响，还考虑了两个变量之间的短期相互作用。

1.2 协整VAR模型估计

为估计协整VAR 模型，将样本数据分为两个子集。其中，一个子集用于开发协整VAR 模型；另一个子集用于进行各种模型的样本外预测与评估。根据惯例，总体样本数据的5%～15%用于样本外预测与各种模型的评估。因此根据数据集的大小，设定这两个子集的边界为2005M12：将1975M01～2005M12的数据用于估计模型，将2006M01～2010M06的数据用于样本外预测，总体评估所得预测数据的准确性，并与现有模型所得结果进行比较。

1.3 滞后时间长度选择

由于两个时间序列CCI 与CPI 均是固定的过程，因此在建立模型前，应先评估CCI 与CPI 之间的协整关系。测试CCI 与CPI 之间的协整，首先需要确定VAR 模型中的滞后次数，可以使用模型选择标准来确定VAR（p）模型的滞后长度。文中采用了Hannan-Quinn 信息准则（HQIC），其适用于一般条件下的一致性估计顺序。滞后时间段p的HQIC 定义如下：

1.4 协整检验

协整关系通过跟踪检验与最大特征值检验进行评估。在这些测试中，协整方程仅包含截距。结果如表1 所示，其中第2 列表示原假设，即假设的协整方程数。跟踪测试与最大特征值测试中的p值表示1%显著性水平上的协整方程，用于确定CCI 与CPI之间的协整关系。

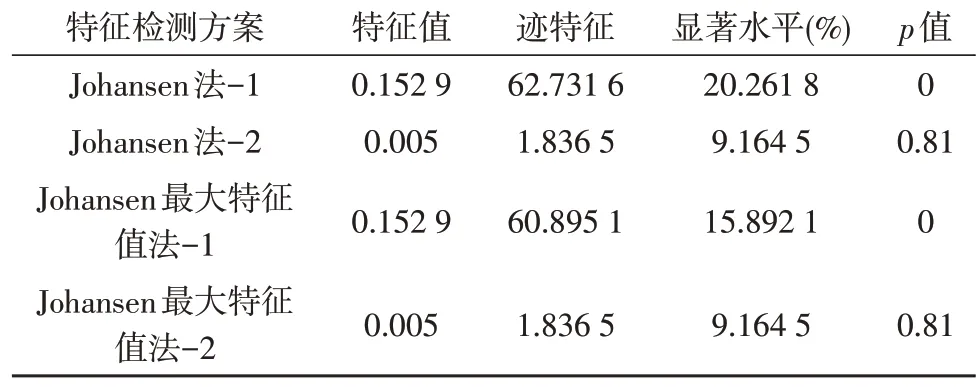
表1 CCI与CPI协整关系测试

2 多网格求解器设计

多核处理器被认为是求解VAR(n)问题的最佳选择，但目前的求解器没有足够的时序可预测性来设计硬件实时（HRT）系统[4]。

文中使用的MERASA 架构具有2～16 个内核[5]，每个内核均具有同时多线程（SMT）设施，旨在支持一个HRT 线程与多达3 个的非HRT 线程[6]。HRT 与共享内存层次结构的本地内存访问具有可预测时间的仲裁策略，但即使硬件具有定时可预测性，计算并行应用程序的WCET 也不是一个简单的过程[7]。

图1 显示了并行代码的结构，主线程与子线程之间的同步点以及子线程之间的同步[8]（PiSj表示“阶段i，步骤j”）。通过这种结构，可以得出整个WCET的第一个细分步骤[9]，如图2 所示。该图结合了代码部分的WCET[10]，其中一些由主线程执行，而其他由子线程执行。根据该图，WCET可以计算为：

图1 并行网格求解器

图2 WCET步骤细分

式中，WCET(main)是在不考虑等待时间的情况下计算出的。

由于迭代步骤中子线程之间的同步，因此需要第二级分析[11]。顺序算法会在循环嵌套的连续迭代之间强制执行数据相关性，将3D 域划分为多个隔离专区后，每个分区均与其相邻隔离专区的边界有依赖关系，这可能造成数据共享，会耗费过多的资源[12]。

由于数据共享模式是规则的，且可以计算整个插值步骤的WCET[13]，所以在最后一个线程完成当前迭代之前，就需要开始外循环的新迭代。

结果将每个计算部分的WCET记为Wi且NUM_ITE 是迭代次数，则迭代步骤的WCET可由式（9）计算[14]：

文中使用兼容POSIX的互斥锁与条件变量来实现线程间同步[15]。图3 为互斥锁Mutex_lock 函数的流程。

图3 互斥锁Mutex_lock函数流程

从图3 可知，线程尝试获取互斥锁有4 种不同的情况[16]。若互斥锁是未被占用的，线程将获取防护锁，然后将其释放。若互斥锁由另一个线程持有，则该线程将在获得防护锁之后挂载在互斥锁上。若另一个线程释放了互斥锁，则所有挂起的线程均将尝试获取互斥锁。

并行多网格求解器的主线程与子线程间的同步依赖于共享变量，该共享变量指示出了要执行的下一个步骤。其包括一个互斥锁（以保护对共享变量的访问）与在变量未处于预期状态时的等待条件。对于N个子线程，操纵锁的线程数和条件为N+1。在主线程与子线程代码中标识可以持有锁的路径：这些路径的最大WCET乘以N+1 表示锁定的Tw3项。在子线程到主线程同步时，每个线程均有自身的状态变量，该变量仅与主线程共享。通过与每个子线程相关的状态变量，来实现两个子线程之间的同步。

3 数据验证与分析

文中使用MERASA 多核处理器对建筑造价数据进行分析，包含2～8 个可用于计算线程的内核（主线程包含一个额外的内核）、完善的ISP（所有指令均可以从指令暂存器中获取）、DSP（用于堆栈数据的暂存器）、循环总线以及5 周期的DRAM 延迟。由于循环策略以及实时线程与非实时线程之间的内核仲裁机制，对于n内核配置，访问主内存的最坏情况延迟为5·n+12。

为了确定置信区间并分析建筑成本的风险与不确定性，文中添加了蒙特卡洛技术来模拟未来成本指数与工程成本。首先，对2006 年1 月的CCI 进行仿真，然后将该值用于仿真下个月的值，以此类推，直到2010 年6 月，重复10 000 次。

图4 为样本外的预测与误差带，正负一个标准偏差与两个标准偏差。自2008 年6 月以来，CCI的急剧上升意味着成本上升的风险较高。2008 年最后4 个月的实际CCI 值超出了预期CCI的两个标准差，这与金融危机的爆发相吻合。

图4 样本外预测与误差带

根据图4 中的预测值，可以较容易地计算出施工成本的上升因子。例如，在2005 年12 月～2006 年1 月的成本上升因子等于2006 年1 月的预测值除以2005 年12 月的CCI的比率，用f表示。在此示例中，2005 年12 月的CCI 为7 647，而2006 年1 月的预测为7 646.43。因此，2006 年1 月的成本上升因子为f1=7 646.43/7 647=0.999 9，而2006 年2 月的成本上升因子为f2=7 650.59/7 647=1.000 5。

为了更加具体地评估工程成本的风险，进行如下数据实验。假设建设项目的计划工期是2006 年1月～2006 年12 月，预算在2005 年12 月制定，基本成本约为9 455 万元。

基本成本的分配在2006M01～2006M12 之间，其根据工程组织计划而变化，且分配的基本成本是随机变量。为便于计算，前5 个月分配的基本成本是相同的，从最小值545 万元到最大值765 万元统一分配。随后4 个月的基本成本呈正态分布，平均值为825 万元，标准差为410 万元。最后3 个月的基本成本也呈正态分布，平均值为960 万元，标准差为490万元。令ci(i=0,1,2,…,12)表示每个月分配的基本成本，可以将预期调整后的成本计算为E(fi×ci)=E(fi)×E(ci)，其中fi与ci相互独立。工程总成本可计算为：

其中，fi与ci是随机变量，因此总成本C也是随机变量，其分布可以通过蒙特卡洛模拟获得。图5为仿真得出的工程总成本分布。

图5 总成本分布实验

分析图5 可知，平均总成本约为9 589 万元，略高于基本成本。总建筑成本从4 961～14 036 万元（标准差为1 220 万元）不等。偏度约为-0.02，峰度为2.99。因此，总建筑成本遵循正态分布，平均总成本为9 589 万元，标准差为1 220 万元。由于可以获得任何百分位的数值，该分析系统还有助于评估电网工程的成本风险。例如，第25 个百分位数大约为8 780 万元，而第75 个百分位数大约为1.043 6 亿元，这表示该成本低于8 780 万元的概率为25%，而成本高于1.043 6 亿元的概率为25%。这样，风险承受能力低的决策者可以将工程成本定在第95 个百分位，约为1 029 亿元；而风险承受能力强的决策者可能将其建造成本定在第25 个百分位数，即约8 780 万元。

4 结束语

文中使用协整VAR 模型分析电网工程造价数据。采用1975M01～2005M12的样本数据建立了估计协整VAR 模型，并使用2006M01～2010M06的数据进行了样本外预测，所得样本外的预测结果证明了预测准确性。为对大量的协整VAR 模型分析工程造价数据进行分析计算，文中使用基于多网格技术的低成本与低功耗的多核处理器设计求解器，解决了现有设计通常与求解时最坏情况的时间分析不兼容问题。结果表明，与其他测试方法相比，协整VAR模型可以提供更准确的分析预测。同时，可以使用协整的VAR 模型来确定置信区间，并评估工程成本上涨的风险与不确定性。