基于弃光消纳的光储系统容量优化配置研究∗
任荣荣,谢丽蓉†,徐波丰,郑 浩 ,王凯丰
(1.新疆大学 可再生能源发电与并网技术教育部工程研究中心,电力系统及发电设备控制和仿真国家重点实验室风光储分室,新疆乌鲁木齐 830047;2.特变电工新疆新能源股份有限公司,新疆乌鲁木齐 830000)
0 引言
近年来,我国光伏发电装机容量增速很快,2019 年全国光伏发电量高达2 243亿千瓦时,弃光电量46亿千瓦时,西北地区弃光问题尤为突出,其弃光电量占全国的87%[1].为了缓解弃光消纳问题,西北地区利用电采暖、开展光热、电池等储能措施,提高光电的上网空间[2,3].储能技术是推动世界能源清洁化、电气化和高效化,实现全球能源转型升级的核心技术之一[4,5].因此,研究如何提高经济性与储能系统容量的合理配置具有一定的实际意义[6,7].
关于储能与可再生能源容量配置方面的研究,文献[8]提出了一种基于非参数核密度估计的光储系统容量最佳配置方法;文献[9]探讨了如何利用储能减少风电的预测输出功率与实际光伏电站输出预测功率的误差,研究储能功率和系统容量的配置;文献[10]提出一种基于额定系统容量条件下对发电单元进行系统容量优化和配置的方法,采用遗传粒子群算法对模型进行求解;文献[11]分析新能源系统输出的高功率低通滤波器的频谱和功率,以确定最佳的低通滤波器截止频率和储能系统的最佳滤波器容量.但上述研究未涉及基于弃光消纳策略的储能容量优化配置方法,所采用的算法也比较传统,且未进行多种算法对比分析.上述文献主要进行了风/光储联合发电系统容量的优化配置方法研究,并未对新能源结合常规能源以及考虑弃光因素下对最佳容量配置展开研究.本文在上述研究的基础上,以系统经济最优为目标,提出一种基于弃光消纳的光储系统容量优化配置方法,其次建立火、光储系统容量优化配置模型,考虑储能电池容量及充放电最大功率约束,采用鲸鱼算法求解储能最佳容量和功率,并确保弃光率控制在5%以内光储发电系统的净收益最大.最后根据新疆某光伏电站的数据进行经济性分析,结果表明采用鲸鱼算法的消纳策略能够实现弃光消纳的目的,使系统收益最大.
1 基于发电功率时变特性的光储发电系统
1.1 光储发电系统
光储发电系统分为源侧和负荷侧,由于现阶段常规机组出力仍占有主导地位,电力源由光伏电站、常规火电厂、新能源储能电站组成,光储发电系统供电结构如图1所示.

图1 系统供电结构图Fig 1 The system power supply structure diagram
当光伏理论出力大于负荷需求时,将弃光存储到蓄电池中,当光伏理论出力不能满足负荷需求时,蓄电池放电尽可能满足负荷需求,以达到“削峰填谷”的效果,进而提升光伏电站的弃光消纳能力.
1.2 弃光消纳策略
光伏出力具有随机性、不确定性,电池储能系统在整个系统中起着能量缓冲作用,火力发电是电力发展的主力军,可以确保系统的稳定性.因此为减少弃光电量,该文针对储能系统SOC和充放电功率制定光伏消纳策略,划分为蓄电池总层(总层)、协调控制层(主层)、充放电分配层(子层)以及经济分析层(子层)4层.弃光消纳策略如图2所示.
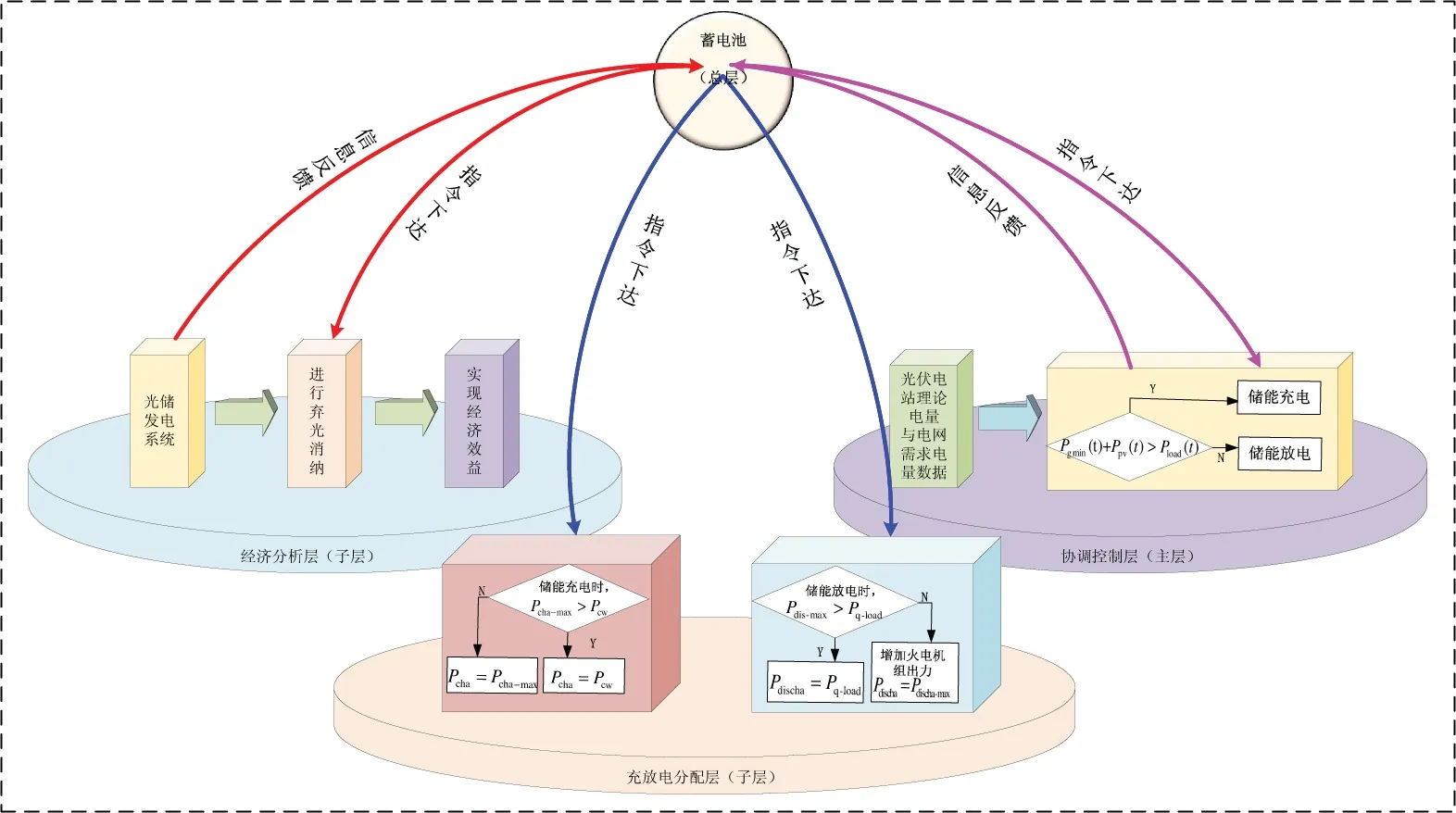
图2 弃光消纳策略Fig 2 Strategy of photovoltaic power curtailment consumption
(1)蓄电池总层.以经济性为控制目标,实现光储系统对弃光电量的消纳,减少储能装置的充放电次数,延长蓄电池的使用寿命,以提高储能装置的经济效益;向协调控制层传达电网并网指令交换计划等,保障各层协调运行以及电网安全.
(2)协调控制层.依据总层传达的电量交换计划,结合本层的光伏电站理论电量与电网需求电量数据,以蓄电池光储协调控制系统实用性与可循环性为控制目标,并为充放电分配层和经济分析层制定控制指令.
(3)充放电分配层.将储能装置分化为充电和放电两种状态,火电机组最小出力和光伏出力一起满足负荷需求,当火电机组出力和光伏出力满足且超出负荷需求时,此时储能需要进行充电,储能系统不能完全吸收超出的负荷需求时,出现弃光现象,当火电机组出力和光伏出力远远不能满足负荷需求时,此时储能系统进行放电,同时增加火电机组出力.充放电分配层主要存在下面两种状态.
(a)储能系统充电:若火电机组最小总出力Pg_min和光伏出力Ppv大于负荷Pload需求时,储能系统吸收超出负荷需求的功率,即Pcw为超出负荷需求的功率.根据储能系统的SOC和充电功率约束计算此时储能系统充电功率Pcha,当Pcw>Pcha_max时,储能系统以最大充电功率进行充电,即Pcha=Pcha_max,将超出部分功率作为弃光功率;当Pcw≤Pcha_max时,储能系统充电功率Pcha=Pcw,储能系统将完全吸纳超出负荷需求的功率,此时不会出现弃光现象.
(b)储能系统放电:若火电机组最小总发电出力Pg_min和光伏发电出力Ppv小于负荷Pload需求时,储能系统进行放电,Pq_load为未满足负荷要求的机组提供剩余发电功率.由储能系统的SOC和放电功率约束可以计算此时储能系统放电功率Pdischa,当Pdischa_max≥Pq_load时,储能系统能够满足剩余负荷需求,即储能放电功率为Pdischa=Pq_load;当Pdischa_max (4)经济分析层.根据光储发电系统,采用弃光消纳策略,对电池组进行协调,从光电售电收益、火电收益、火电机组燃料成本、储能电池成本、弃光惩罚5个方面考虑系统净收益最大,构建优化模型以实现蓄电池储能电站在一天内的最大净收益. 2.1.1 目标函数 光储发电系统优化调度的实质是在允许蓄电池运行的条件下,对电池组进行协调,以实现蓄电池储能电站在一天内的最大净收益.燃煤电厂发电所需主要能量来源是动力煤,煤炭价格决定发电的主要成本.一般情况下,煤炭价格占发电成本的60%左右,因此传统的电力系统经济调度一般以发电所需燃料成本最低为目标函数[12].本文主要以光电售电收益、火电收益、火电机组燃料成本、储能电池成本、弃光惩罚5个方面构建优化模型以实现系统净收益最大,目标函数如式(1)所示: 式中:Fmax为系统净收益最大;Ig为光电售电收益;Hg为火电收益;Cg为火电机组的燃料成本;Cd为折算至每天的储能成本;Cp为弃光惩罚. (1)光电售电收益 光储电站的成本和收益主要通过光伏售电额计价来实现,由于我国储能发电系统光伏上网的成本和电价没有统一的电价规定[13],因此本文在我国光储电站的统一成本计价模式下重新建立了收益分别计价函数.收益分别计价函数和Δt时长内可计算售电额,如式(2)、式(3)所示: 式中:Ig为光电调度售电收益;T为调度总时段;Ig(t)为Δt时长内的调度售电额;βsta为光伏发电调度上网出力的标杆调度电价;βb为储能上网出力统一调度上网电价,当光储出力统一调度售电价时,βsta=βb. (2)火电收益 式中:Hg为火电收益;βf为火电上网电价;N为火电机组数量;Pgi(t)为采样时刻火电机组总出力. (3)火电机组的燃料成本 式中:Cg为火电机组的燃料成本;ai、bi、ci为火电机组i的煤耗系数;Pg为火电机组的发电功率. (4)储能系统总成本 式中:Cess为储能系统总成本;A、B、C、D为储能成本系数;Pess为储能功率;Sess为储能容量. (5)折算至每天的储能成本 式中:I为折旧率,取值为0.01;Yr为寿命,取值为10年,IT=(1+I)Yr. (6)弃光惩罚 式中:Q为弃光电量,目标函数设立该项的意义在于让储能系统尽量吸收弃光功率,来消除或降低弃光功率. 2.1.2 运行约束 (1)功率平衡约束 系统有功功率平衡,即任意时刻的并网功率应与光储出力相等: 式中:Pload(t)为采样时刻负荷功率;Ppv(t)为采样时刻光伏出力;Pess(t)为采样时刻储能出力;Pgi(t)为采样时刻火电机组总出力. (2)储能功率约束 储能充放电功率受限于变流器最大转换功率: 式中:Pmax(t)为储能系统最大放电功率;Pess(t)为采样时刻储能出力;储能系统放电为正值,充电为负值. (3)储能SOC约束 式中:t为优化调度时间,根据优化调度进程进行取值,采样时间间隔为10 min,取值范围为[0,144].SOC(t−1)为储能系统前一时刻荷电状态;为防止储能过充过放,设置SOCmin、SOCmax为储能最小、最大荷电状态;η为储能电池充放电效率. (4)储能容量约束 式中:Smin、Smax为储能电池最小、最大配置容量. (5)充放电次数约束 考虑到现有技术,经实际调研可知,本文设置储能系统充放电次数M值为1. 鲸鱼优化算法(Whale Optimization Algorithm)是一种通过模拟鲸鱼捕食的行为进行建模得到的新型优化算法.分为包围猎物、狩猎行为、搜索猎物3个阶段.研究表明,鲸鱼算法与传统算法相比具有算法机制优势,原理简单、易于实现、寻优精度高,收敛速度快,且几乎不涉及参数设置,近两年成为进化计算领域重要的改进算法之一[14].为更好求解大规模工程优化问题,提升算法全局寻优性能和应用能力,加快算法收敛速度,增强求解稳定性,本文采用WOA算法求解优化模型,对系统收益最大时的储能容量和功率以及各个火电机组出力进行计算. (1)包围猎物.座头鲸在寻找到猎物之后能够迅速包围猎物,且更新位置,将处于最佳围捕位置的当前鲸群作为目标猎物或接近最佳目标猎物,位置更新的数学表达式为: 式中:a为进行迭代时从2线性下降到0的向量;r为[0,1]之间的随机数;M为最大迭代次数. (2)狩猎行为.座头鲸是利用螺旋状运动的方式进行狩猎,其数学模型为: 在这里,必须指出的是,若鲸鱼在捕捉到猎物的收缩圈周围内同步沿着一个螺旋形的路径进行游动,同时沿着另一个螺旋形游动路径的方向进行,为了更好地模拟该鲸鱼的行为,在优化的过程中选择收缩圈的包围游动机制和螺旋形路径位置更新的概率相同,均为0.5.其数学模型为: (3) 搜索猎物.当A ≥1时,在这个模型中会随机地生成一个用于搜索鲸鱼的代理,对搜索其他鲸鱼的数量和位置以及如何更新其他的鲸鱼在整个鲸鱼群系统中的数量和位置都进行了选择,从而有效地使其远离了猎物.增强了搜索算法的灵活性和全局探索的能力.其数学模型为: 图3 算法流程图Fig 3 Algorithm flowchart 以新疆某200 MW光伏电站与一个600 MW和一个700 MW火电厂为例,将10 min作为采样时间间隔,选取典型日光伏电站理论电量与电网负荷需求电量数据以及5台火电机组数据进行仿真.由于蓄电池技术成熟,容量大,广泛应用于电力系统中[15,16],故本文选用蓄电池作为储能方式.表1为算例参数,表2为火电机组相关参数,图4为典型日运行曲线. 表1 算例参数Tab 1 The simulation parameters 表2 火电机组相关参数Tab 2 The thermal power unit related parameters 图4 典型日运行曲线Fig 4 Typical daily operating curve 为说明所建模型的有效性,在相同的系统参数下,对2种运行工况进行对比,2种工况如下: 工况1:不考虑弃光消纳策略,储能系统不参与工作. 工况2:考虑弃光消纳策略,利用鲸鱼算法对目标函数进行优化. 对上述2种工况下的弃光电量、光伏电站出力、火电机组出力情况进行分析比较.选取200 MW光伏电站与一个600 MW和一个700 MW火电厂作为本文的研究对象.在相同的系统参数下,分析2种工况下弃光电量的情况,如图5所示. 由图5可知,工况1和工况2对比,采用了弃光消纳策略后,工况2弃光电量明显降低,有效消纳更多光伏.为保证系统安全可靠运行,选取5台火电机组的输出数据,采样时间间隔为10 min,利用表2列出的火电机组参数分析2种工况下火电机组出力变化曲线,如图6所示. 图5 弃光电量对比图Fig 5 Comparison diagram of abandonedpv electric quantity 由图6可知,采用弃光消纳策略后,在00:00―14:00与18:00―24:00这两个时间段,储能系统不进行工作,工况1和工况2火电机组出力相同;而在14:00―16:00与16:00―18:00之间,由于储能参与出力,工况1和工况2的火电出力不同且出现较大差异,在此主要分析14:00―16:00与16:00―18:00 时间段的火电机组出力情况.即在14:00―16:00之间,火电机组按照最小出力,储能进行充电;在16:00―18:00之间,火电机组相对前一时段出力增加,相较于工况1,工况2火电机组出力明显下降,储能进行放电.2种工况下光伏电站实际出力曲线,如图7所示. 图6 火电机组出力对比图Fig 6 Comparison diagram of thermal power unit output 由图7可知,采用弃光消纳策略后,工况1和工况2对比,在00:00―14:00与18:00―24:00这两个时间段,储能系统不进行工作,工况1和工况2光伏电站出力相同;而在14:00―16:00之间,由于储能参与出力,工况1和工况2的光伏电站出力不同且出现较大差异,在此主要分析14:00―16:00时间段的光伏电站出力情况.即在14:00―16:00之间,工况2光伏出力明显增加,此时光伏增加的出力一部分用于满足负荷需求,另一部分通过储能系统进行存储;在16:00―18:00之间,储能进行放电,工况1和工况2光伏出力相同.由上述分析可知,工况2有效消纳了更多光伏.储能电池的充放电功率如图8所示,储能电池的荷电状态变化如图9所示. 图7 光伏电站实际出力曲线Fig 7 Actual output curve of photovoltaic power plant 图8 储能电池的充放电功率Fig 8 Charge and discharge power of energy storage batter 由图8可知,在14:00―16:00之间,储能电池进行充电,在16:00―18:00之间,储能电池进行放电,其余时段不进行充放电,保持恒定状态. 由图9可知,SOC满足区间0.1~0.9的要求.储能系统进行一次满充满放,不仅减少了储能系统充放电的频次,而且有效保证储能电池的寿命,符合实际储能电池运行状态的要求. 图9 储能电池SOC变化Fig 9 SOC change of energy storage battery 根据光储系统容量优化模型,得到系统净收益与储能系统功率、储能系统容量的关系,结果如图10所示. 从图10可以看出,储能容量与系统的净收益和功率呈正相关,系统净收益随着储能系统容量的增加而增加,且随着储能功率的增加,系统净收益并未一直增加.本文采用鲸鱼算法对光储系统容量优化模型求解可得,当储能功率为22.10 MW、容量为31.83 MW·h时对应的系统净收益最大,为4 650 936元. 图10 优化结果Fig 10 Optimization results 本文分别采用遗传算法、自适应粒子群算法、鲸鱼算法三种优化算法对光储发电系统净收益进行求解,计算结果见表3,收敛曲线如图11所示. 图11 收敛曲线Fig 11 Convergence curve 由表3可知,遗传算法、自适应粒子群算法和鲸鱼算法在弃光率均为2.9%的情况下,最优储能容量分别为35.00 MW·h、33.31 MW·h、31.83 MW·h.本文用三种算法对目标函数优化求解,发现鲸鱼算法有一定的优势,因此利用鲸鱼算法对目标函数进行优化. 表3 计算结果Tab 3 The calculation results 由图11可知,最大迭代次数为500,随着迭代次数的增加,在满足约束条件的情况下,遗传算法、自适应粒子群算法、鲸鱼算法分别经过152、108、84次迭代之后,迭代过程逐渐趋于稳定,并得到系统净收益最大,分别为4 648 653元、4 649 921元、4 650 936元.仿真结果表明,在光储发电系统中,鲸鱼算法相比遗传算法和自适应粒子群算法收敛速度快且能够找到更优解. 本文提出基于光储发电系统的弃光消纳策略,利用该策略制定储能系统充放电状态框架,在提高储能装置经济性的同时,实现弃光的最大消纳.主要结论如下: (1)本文所提出基于光储发电系统的弃光消纳策略,以光伏消纳为优先原则,将光储联合火电厂满足负荷供电需求,构建以光储系统日内最大净收益目标函数的模型. (2)以新疆某光伏电站数据进行分析,在光伏电站加装储能系统能够大幅度提升整个系统的友好调度能力,使该地区弃光率从12.7%降为2.9%,最佳的储能容量为31.83 MW·h,其系统最大净收益为465.09万元. (3)在求解大规模工程优化问题上,相比于遗传算法与自适应粒子群算法,鲸鱼算法具有收敛速度快、寻优精度高、更易找到全局最优解的优越性. 由于储能应用工况收益率对于电池的单次充放成本有较大的敏感性,而电池循环寿命将极大程度上影响储能电池实际的单次充放成本,因此提升电池循环寿命也将成为未来储能电池的发展方向.2 建立光储系统容量优化模型
2.1 最大净收益模型


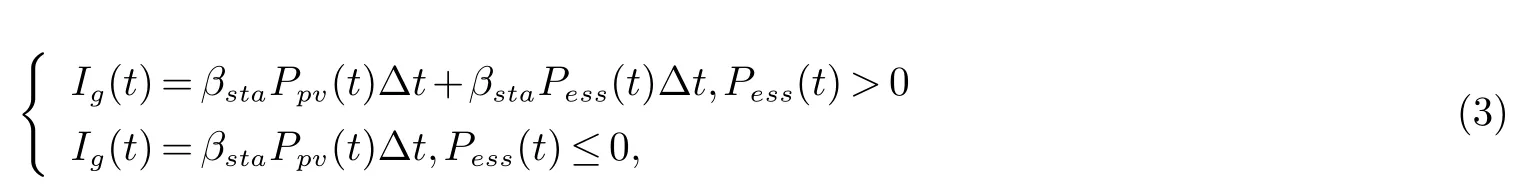









2.2 鲸鱼算法求解优化模型



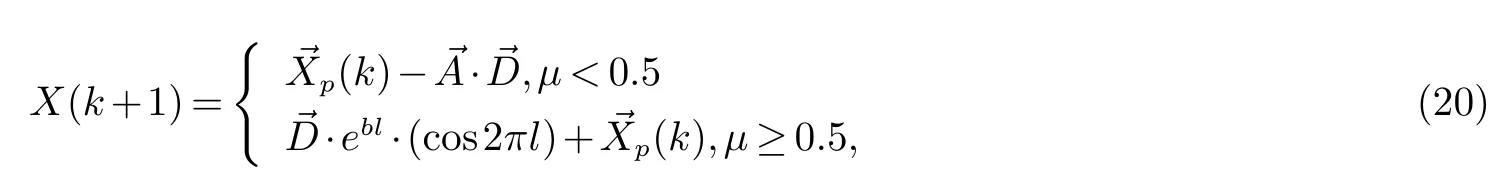


3 算例分析
3.1 数据提取



3.2 容量优化配置结果分析
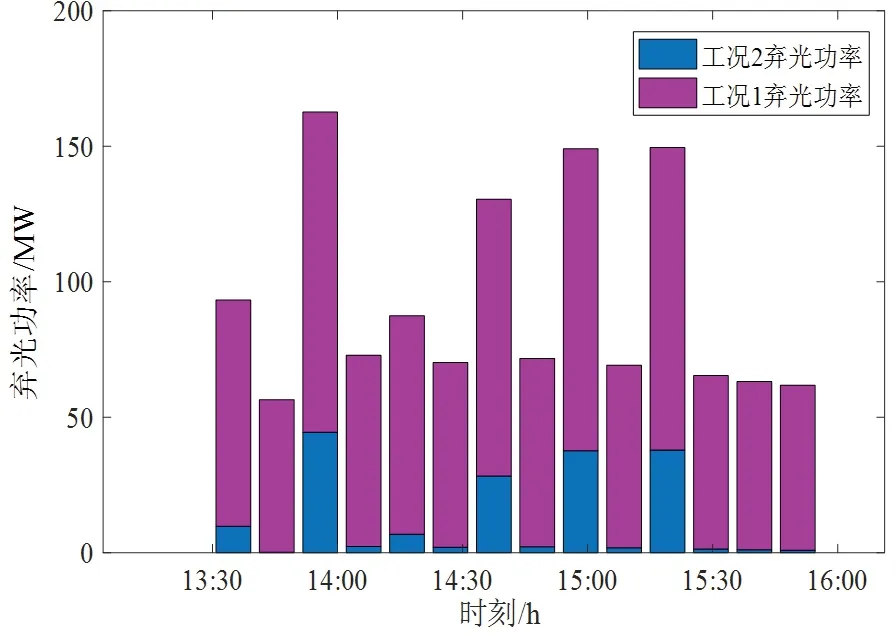
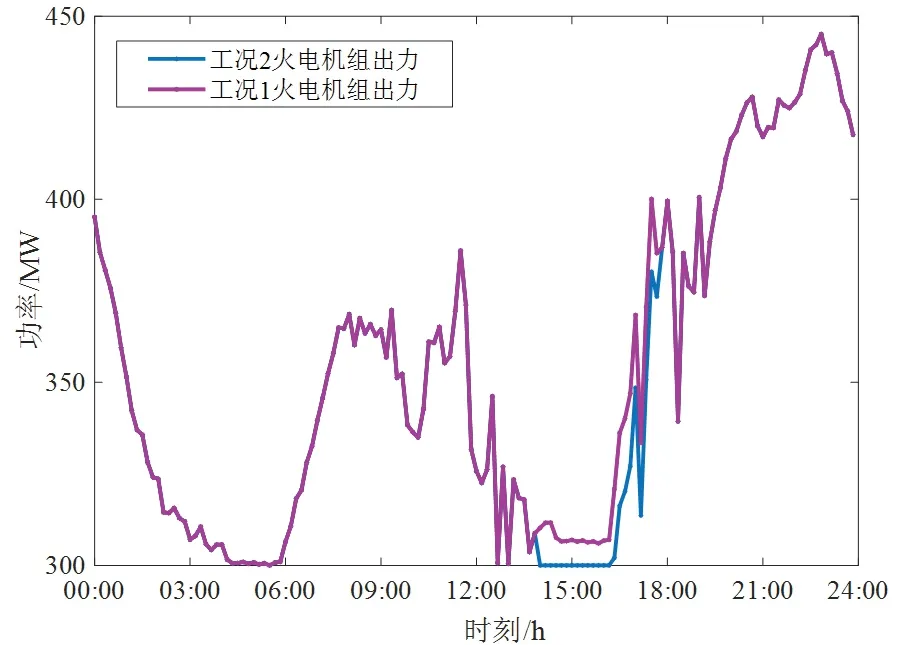
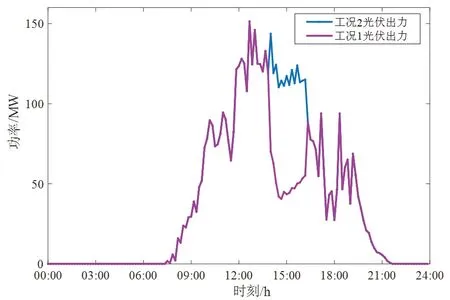

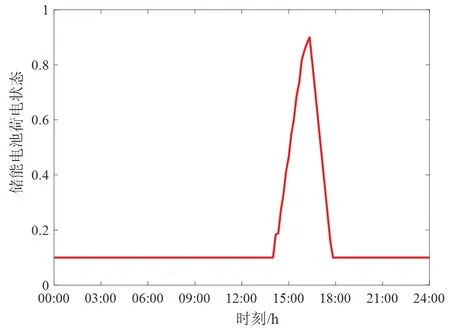

3.3 算法对比


4 结论

