新疆哈密特高压直流送端电网地表电位与直流电流分布研究∗

樊艳芳，曾 富

(新疆大学 电气工程学院，新疆 乌鲁木齐 830047)

0 引言

特高压直流输电系统因具有输电容量大、输送距离远、损耗小等优点而被广泛使用[1−3]，但直流输电系统采用单极-大地回路运行时，将有数千安的直流电流由接地极注入大地，在接地极周围的特定区域形成恒流场，影响地表感应电势分布.地表电势位可以导致直接接地变压器的中性点处产生直流电流分量，当流入变压器绕组的直流分量超过一定范围时，磁芯将发生饱和，电流波形会改变，导致变压器偏磁，使变压器总励磁电流变成尖顶波，导致变压器振动增大、损耗增加等问题[4−6].

地表电位的准确求解是计算直流电流在交流电网中分布情况以及预防和抑制直流偏磁的重要环节[7−9].直流接地极周围的地表电位分布受直流输电系统的运行方式、接地极的尺寸、形状以及接地极附近大地的参数等多方面影响，其中复杂地貌条件下的大地参数是分析地表电位的难点[10−12].近年来，针对地表电位分布的计算，已取得很大的进展.文献[13]提出了适用于求解水平土壤分层或者垂直分层格林函数的递推方法，这种方法可以在计算机中快速计算；文献[14]对文献[13]的格林函数公式做了相应的简化，使计算进一步简便.但上述方法没有考虑地下土壤结构和电阻率的复杂性，实际土壤的分布是不均匀的，采用均匀或浅层土壤模型计算会产生一定的误差.文献[15]采用有限元方法，使用ANSYS 软件建模仿真求解地表电位，并分析了大地内部构造、土壤模型精度地表电位分布计算的影响.新疆电网是一个特高压交、直流送端电网，新疆哈密存在较多的高山和断裂，地下土壤结构非常的复杂，需要建立更为复杂的大地土壤结构模型来分析接地极附近地表电位分布，减小计算的误差.

本文采用镜像法与行波法，考虑电流波的折射与反射，建立了水平3层以及水平4层土壤结构模型，分别计算不同土壤模型下的地表电位和直流偏磁电流分布.在MATLAB中构建±800 kV新疆哈密-郑州直流输电工程送端电网仿真模型，讨论了不同土壤分层模型对直流偏磁电流分布的影响，为后续直流偏磁的预防与治理工作提供参考.

1 不同土壤分层模型下地表电位计算

1.1 无限大均匀大地模型

根据电流的连续定理，可以得到无限大均匀土壤模型中直流接地极附近地表电位：

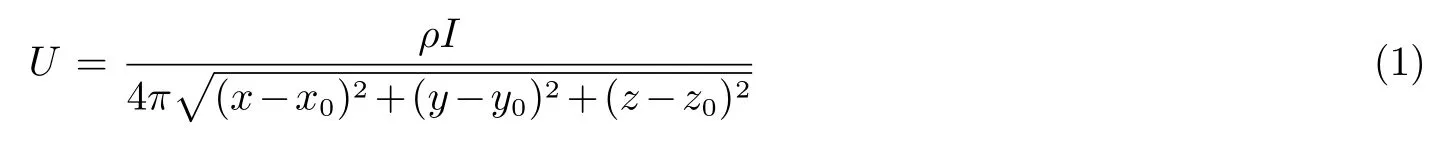
式中：x,y,z为待求点的坐标；x0,y0,z0为电源点的坐标；ρ为介质的电阻率Ω·m；I为电源点的电流.

1.2 水平2层土壤模型

当直流接地极所在区域地貌结构较为单一时，采用水平2层土壤分层结构.一般情况下接地极埋在地下5米左右，而实际情况中水平第一层的深度远大于5米，因此，在水平土壤分层的情况中只考虑直流接地极与交流接地极在同一分层的情况.水平2层土壤模型如图1所示，第一层与第二层的厚度分别为H1和∞，电阻率分别为ρ1和ρ2，直流电源深埋为h，直流接地极的入地电流为I，坐标为(x0,y0,z0)，第一层中任意一点Q（x,y,z）处的感应电势为U.

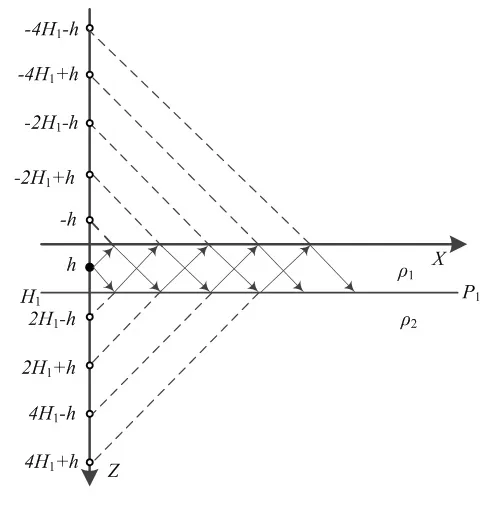
图1 水平2层分层模型Fig 1 Horizontal 2-layer layered model

当大地为水平2层分层时，根据行波法与镜像法，电流源在土壤内传播时，会分别向上和向下传播.向上传播时，遇到地面会发生反射，反射率为k0，然后继续向下传播遇到第一层与第二层分界面P1时又会发生反射，反射率为k1，之后会在土壤内反复发生反射.同理电流波在向下传播时，首先会遇到P1发生反射，反射率为k1，然后继续在土壤内发生反射.如果把电流波遇到分界面时发生反射的反射波的延长线等效为一个镜像点的作用（大小为反射波的大小，电流波每发生一次反射就变为原来的k倍，k为反射率），那么水平第一层中任意一点Q的感应电势为所有镜像点加电源点共同作用的结果.根据波的反射，即可得到Z轴上等效点的坐标分别为±（2nH1±h），且等效点的电流大小为Ikn1，由此可以得到水平第一层中任意一点Q的感应电势U为：

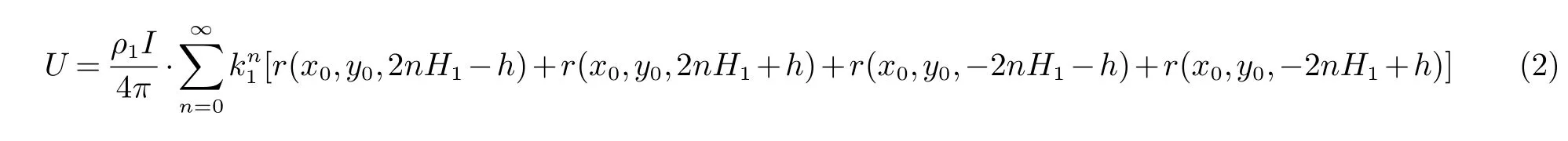
式中：r(x0,y0,z0)为点(x0,y0,z0)到点(x,y,z)的距离，即：

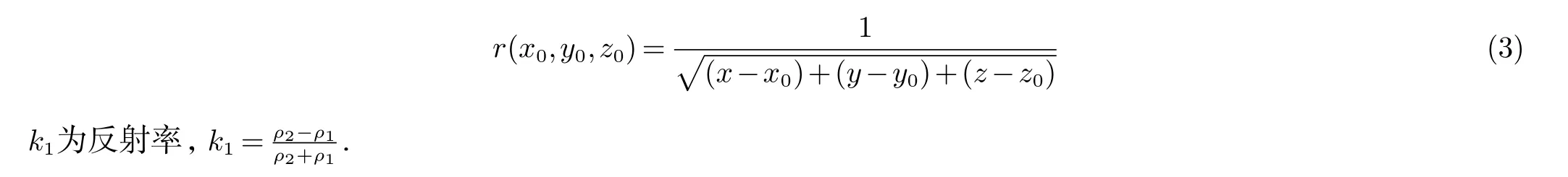
1.3 水平3层土壤模型

当大地采用水平3层分层模型时，分层模型如图2所示，电源点位于地下h米处，H1,H2分别为第一层与第二层土壤的厚度.电流波在大地中的传播过程中遇到不同土壤介质的分界面时会发生波的反射与折射.电流波向上传播遇到地面会发生反射，反射率为k0，由于地表上的电阻率为0，所以k0=1；向下传播遇到第一层分界面会发生折射与反射，反射率为k1，折射率为T1，折射波遇到第二层分界面时又会发生反射，反射率为k2，继续向上传播遇到水平分层面P1折射进入水平第一层，折射率为T2，如果忽略折射角，即可得到Z轴上等效点的坐标为：±(2nH1±h)，2n(H1+H2)±h,-2n(H1+H2)±h，电流分别为I·k1、(T1k2）·I、（T1T2k2）n·I.因此，地表电位的计算可以将一个电源点的作用转换为多个镜像点共同作用的结果，即水平第一层土壤中任意一点的地表电位为：

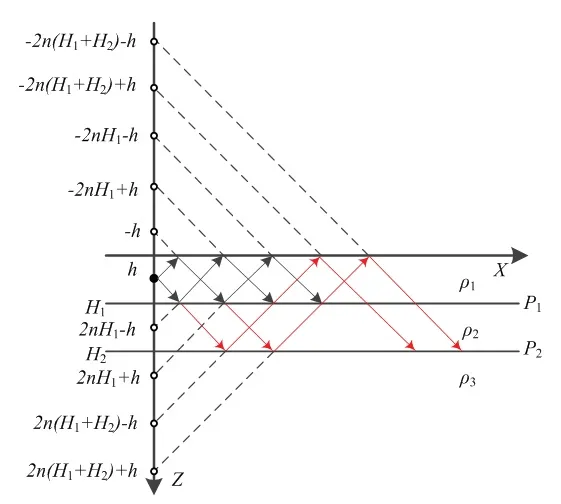
图2 水平3层分层模型Fig 2 Horizontal 3-layer hierarchical model

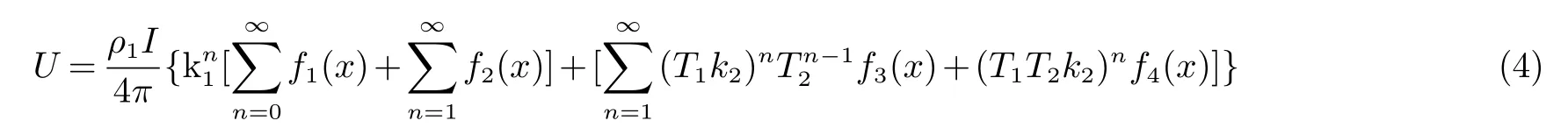
式中：k1,k2分别为第一层，第二层分界面的反射率，T1,T2为折射率：T1=1-k1,T2=1+k1;f1(x)=r(x0,y0,A)+r(x0,y0,B)，f2(x)=r(x0,y0,-A)+r(x0,y0,-B)，f3(x)=r(x0,y0,C)+r(x0,y0,D),f4(x)=r(x0,y0,-C)+r(x0,y0,-D),A=2nH1−h,B=2nH1+h,C=2n(H1+H2)-h,D=2n(H1+H2)+h.这样就将水平3层模型转换为无限大均匀大地模型.

1.4 水平4层土壤模型

当大地采用水平4层土壤结构模型时，分层模型如图3所示，其中ρ1-ρ4，H1−H3分别为各层土壤的电阻率与深度.与水平3层模型下相似，电流波在传播过程中遇到各层土壤的分界面时会发生反射，当电流波进入另一层土壤时，会发生折射.在水平3层分层模型的基础上，电流波到达水平2层与水平3层的分界面P2时，电流波不仅要向上发生反射，还会继续向下传播折射进入水平第3层土壤中，当电流波遇到第3层与第4层土壤分界面时，电流波会发生反射，向上传播，反射率为k3.因此，在Z轴上的等效点坐标为：±（2nH1±h），2n(H1+H2)±h,-2n(H1+H2)±h，2n(H1+H2+H3)±h,-2n(H1+H2+H3)±h，电流为I·k1、.即水平4层分层模型下，第一层土壤结构中任意一点的地表电位为：

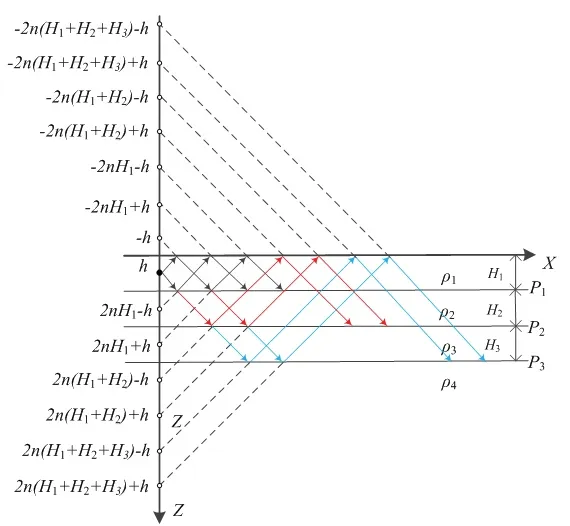
图3 水平4层分层模型Fig 3 Horizontal 4-layer hierarchical model

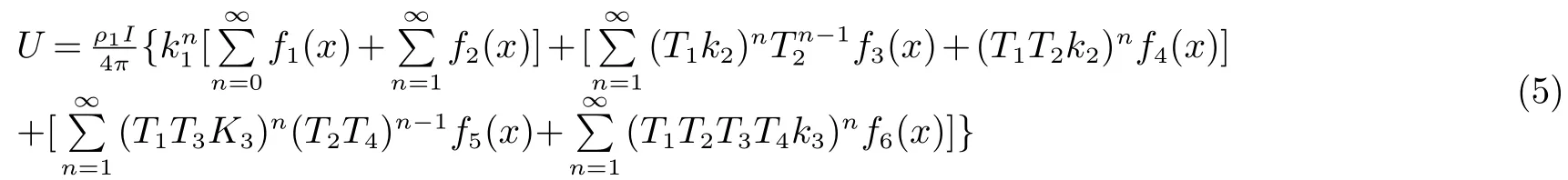
式中：k3为第三层分界面的反射率，T3,T4为折射率：T3=1-k2，T2=1+k2；f5(x)=r(x0,y0,E)+r(x0,y0,F)，f6(x)=r(x0,y0,E)+r(x0,y0,F)，E=2n(H1+H2+H3)−h，F=2n(H1+H2+H3)+h.同理可将4层土壤模型转化为无穷大均匀大地模型下来计算.

2 交流电网中直流电流分布计算

特高压直流输电系统采用单极-大地回路运行时，接地极附近地表电位会发生变化，使相邻两个变电站之间产生电位差，导致交流变压器中性点会有直流电流流入，从而引起直流偏磁问题.本文基于场路耦合原理，由节点电压法计算交流电网中直流电流分布情况.

2.1 交流系统中各元件等值模型

交流系统直流分布计算网络模型主要包括输电线路模型和变压器模型.线路因为只有直流经过，因此线路可以等效为纯电阻线路.变压器分为自耦变压器与其他普通变压器.对于三相三绕组自耦变压器而言，其高压侧与中压侧共用一个绕组，且为星型接地，而低压侧为三角形接地，所以只需考虑高压绕组和中压绕组的等值情况；对于其他类型的三相三绕组变压器，其高压侧、中压侧和低压侧绕组为并联关系，其中高压侧和中压侧为星型接地，低压侧为三角形接地，因此该种类型变压器也只需考虑高压侧与中压侧的等值模型，其等值模型如图4所示.

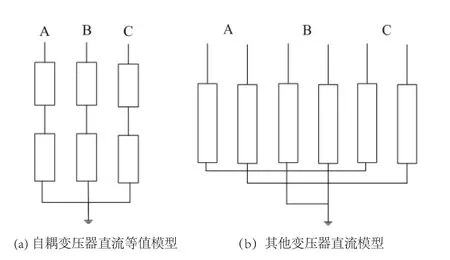
图4 变压器等值示意图Fig 4 Transformer equivalent diagram

2.2 直流偏磁电流分布

设直流接地极附近交流电网中有n个变电站和发电厂，m条母线，将交流电网等值为纯电阻网络，基于场路耦合原理，由节点电压法求得变压器直流：

由图3可知，在pH相同条件下，供试土壤对重金属离子Cd的吸附量随平衡溶液中Cd浓度的增加而缓慢增加，且有机质含量和CEC较高的土样其吸附量增幅明显，这主要是由于有机质含量、碳酸钙含量和阳离子交换量较高土样，其对Cd离子的吸附位点较多。徐晓炎[21]研究土壤Cd吸附特性的结果表明，阳离子交换量与有机碳可影响土壤对Cd的吸附。

式中：I1为交流变电站中每个变压器节点注入电流的列向量（n×1），I2为母线节点注入电流列向量（m×1），G为电导，U1为每个交流变电站接地极处感应电位，U2为母线节点电压.在等值网络中由于母线节点仅起联络作用，因此母线节点的注入电流I2为0，则可以得到流入变压器中性点的直流电流为：

因此，只需要求得直流接地极附近交流电网的地表电位分布即可求得流入各个变电站的直流电量.

3 仿真分析

针对±800 kV哈密南-郑州，天中特高压直流输电工程的送端岌岌台直流接地极对附近交流电网的影响，本文基于MATLAB仿真软件，搭建哈密电网结构，分析不同土壤结构分层模型对交流电网中地表电位分布以及直流电流分布的影响.

3.1 不同土壤模型下地表电位仿真

根据哈密的土壤结构实际情况，选取表1所示3种仿真模型参数，对比分析大地模型分别为水平2层、水平3层、水平4层模型下地表电位的分布情况，如图5所示.

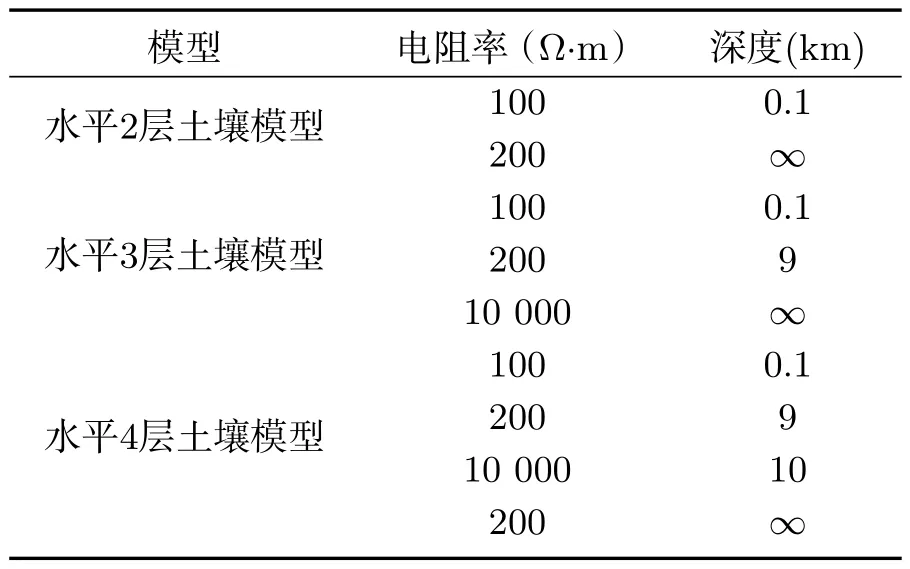
表1 不同仿真模型参数Tab 1 Different simulation model parameters

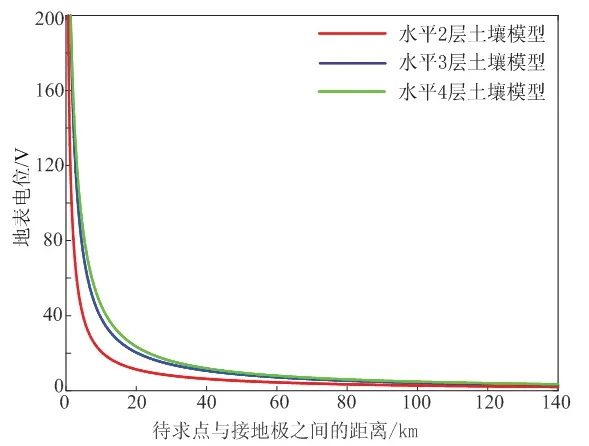
图5 不同土壤分层模型下地表电位分布Fig 5 Distribution of surface potentials under different soil stratification models

由图5可知，随着待求点与直流接地极之间的距离增大，地表电位在不断的减小，并且无论是哪种土壤分层模型地表电位都在待测点与直流接地极距离20 km之前快速下降.20 km之后地表电位下降得非常缓慢，且最终都将降为0，而接地极周围的地表电位不受土壤分层的影响.由此可以看出，地表电位的变化趋势不受土壤分层的影响.

3.2 土壤电阻率对地表电位分布的影响

为分析大地土壤电阻率对地表电位分布的影响，现分别仿真浅层土壤电阻率ρ1和深层土壤电阻率ρ2变化时交流电网中地表电位的分布情况.

分析浅层土壤电阻率ρ1对地表电位分布的影响时，ρ1分别取50 Ω·m、100 Ω·m、500 Ω·m，其他参数保持不变，ρ2=1 000 Ω·m，ρ3=10 000 Ω·m，ρ4=15 Ω·m；分析深层土壤电阻率ρ2对地表电位分布的影响时，ρ2分别取500 Ω·m、1 000 Ω·m、15 000 Ω·m，其他参数不随ρ2的变化而变化，ρ1=100 Ω·m，ρ3=10 000 Ω·m，ρ4=15 Ω·m，仿真曲线如图6所示.

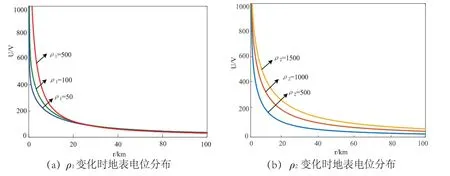
图6 ρ1,ρ2对地表电位的影响Fig 6 Influence of ρ1,ρ2 on surface potential

由图6可知，随着浅层土壤电阻率ρ1与深层土壤电阻率ρ2的减小，地表电位在20 km前下降得越来越快，即ρ1，ρ2的减小加快了地表电位下降，使离直流接地极较远的两个变压器之间的电位差减小，由此可得，如果直流接地极附近浅层与深层土壤电阻率较小可缩小直流接地极引起的直流偏磁影响范围，使较远地区的交流电网免受直流偏磁的危害，在新建直流接地极时考虑这一因素可从源头上抑制直流偏磁对交流电网的影响.

3.3 不同土壤模型下直流电流分布仿真

由前两节的计算公式可计算出交流电网中的地表电位分布以及直流电流分布，以哈密岌岌台直流接地极附近交流电网的实际情况在MATLAB中搭建仿真模型，仿真分析不同土壤分层模型下直流电流在交流系统中的分布，并将其与哈密交流电网中直流电流的实测值做比较，对比每种分层模型下直流电流计算的准确性.

仿真模型中取额定入地电流2 500 A，ρ1=100 Ω·m ρ2=200 Ω·m，ρ3=10 000 Ω·m，ρ4=15 Ω·m，地上交流电网的等效电阻均采用实测值.不同土壤分层模型下直流接地极附近交流电网中直流电流分布情况如图7所示.

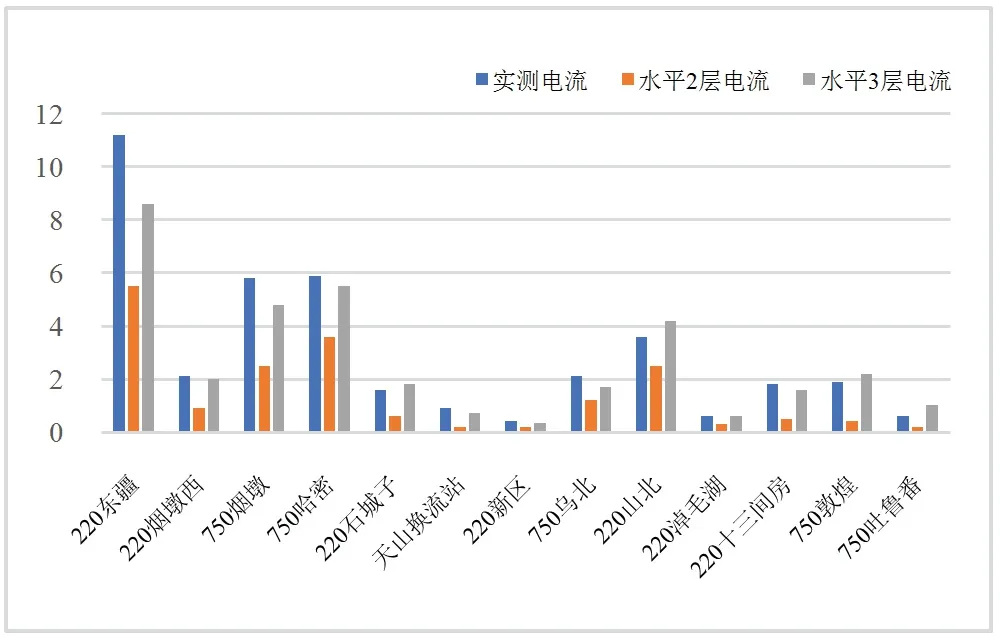
图7 不同土壤分层模型下直流电流分布情况Fig 7 Distribution of DC current under different

由图7可知，相较于水平2层分层模型，水平3层分层模型下计算得到交流电网中的直流电流分布与实测值之间的差值更小.由此可见，在计算直流接地极附近交流电网中直流电流分布时，综合各种因素，采用水平3层分层模型更加符合实际情况.

4 结论

通过分析新疆特高压直流外送电网地表电位与直流电流分布，并对比电网的实测值，得出以下结论：

（1）随着待求点与直流接地极的距离增大，地表电位呈下降趋势，且在距离为20 km前快速下降，20 km后下降缓慢.可见直流接地极在选址时应尽量远离附近有交流变电站的地区，可从源头上降低直流偏磁对交流电网的影响.

（2）相比水平2层模型，水平3层模型下交流电网中直流电流分布的计算结果更为准确.水平3层模型考虑了波的折射，采用的土壤分层模型更加符合实际土壤分层情况，能够满足工程计算要求.后期将在大地深层电阻率精确测量方法上开展进一步研究，以提升直流偏磁电流预测计算精度.